基于神經網絡和遺傳算法的錠子彈性管性能優化
莫 帥, 馮戰勇, 唐文杰, 黨合玉, 鄒振興
(1. 天津工業大學 機械工程學院, 天津 300387; 2. 天津工業大學 天津市現代 機電裝備技術重點實驗室, 天津 300387)
減振彈性管作為紡織錠子的關鍵精密部件,與軸承座和多層吸振卷簧等精密零件相互配合,共同組成了錠子下彈性阻尼錠膽系統。常用類型的精密錠子結構中,減振彈性管因上端與軸承座內孔緊密配合而形成了豎直的懸臂梁結構,配合其特殊的稀疏螺旋槽結構,顯著增加了彈性管軸徑向的彈性,達到對錠子旋轉體高速下自動定心、降低振動、吸收噪音的目的,提高紡紗質量和效率[1]。
目前,全球的紡織制造業發展良好,但針對紡織機械的基礎研究較為薄弱,錠子中減振彈性管是其不可或缺的關鍵零部件,國內外對其研究較少。吳文英等[2]推導了開螺旋槽彈性管的等效抗彎剛度和底部剛度系數的計算公式,分析了彈性管各參數對其剛度及振動性能的影響;王志勇等[3]從理論和實驗數據二方面分析討論了彈性管材料及結構參數對其彈性的影響,同時討論了加工工藝對彈性管彈性的影響;彭來深等[4]通過對彈性管加工工序、裝夾方式、夾具及刀具進行改進,提高了彈性管錠底孔相對外圓的同軸度,有效降低了錠子高速運轉時的振程。由于開螺旋槽部分的結構參數對彈性管整體性能影響很大,而錠子作為精密機械專件,結構的微小變化都會有效提升錠子性能,因此,有必要對減振彈性管的工藝參數進行優化設計,以達到實際工況下的最優性能。
本文將彈性管螺旋槽結構以矩形彈簧近似分析,構建了螺旋槽部分的抗彎剛度及減振彈性管底部振幅的數學模型,并以彈性管性能的主要影響參數槽寬、螺距、壁厚、材料彈性模量為設計變量,結合徑向基神經網絡和遺傳算法對其剛度和底部振幅進行多目標優化設計,實現高速下錠子的穩定性提升。
1 彈性管力學性能分析
將常用錠子減振彈性管的螺旋槽部分按矩形截面圓柱彈簧近似處理,如圖1所示。

圖1 彈性管實物及螺旋槽分析模型Fig.1 Elastic tube physical (a) and spiral groove analysis model (b)
已知減振彈性管抗彎剛度Jeq為
式中:α為彈簧的螺旋角,(°);Bn、Bb分別為彈簧絲截面對主法線和次法線的彎曲剛度,N/m;C為彈簧絲截面對切線的扭轉剛度,N/m。
由于彈性管內部會受到錠桿高速旋轉引起的激振力,造成錠底的摩擦磨損及錠子運行的振動加劇,因此,錠底處(即彈性管底部)振動性能的控制十分重要。圖2示出彈性管底部變形示意圖。

圖2 彈性管底端振動示意圖Fig.2 Vibration diagram of bottom of elastic tube
減振彈性管底部振動幅度A的計算公式為
式中:l2、l3為彈性管相應段的長度,mm;F為轉子由滑動軸承傳遞給彈性管的激振力,N。
結合以上公式并通過實驗研究表明,隨著槽寬c的減小,壁厚h、螺距p、彈性模量E的增大,彈性管剛度增加,底部振幅降低[2-3],可見彈性管剛度和底部振幅2個目標之間是相互制約的,因此,本文提出以遺傳算法來解決剛度和振幅多目標相互沖突的問題,結合徑向基神經網絡(RBF)近似模型,并利用遺傳算法的隨機性和隱含并行性,對彈性管模型進行多目標參數優化,從而獲得給定參數區間的最優解集,達到錠子下彈性錠膽系統彈性管的最優性能。
2 彈性管多目標優化模型
2.1 彈性管優化目標選擇
由上述分析可知,對于豎直懸臂梁結構的彈性管來說,降低彈性管剛度:一方面代表彈性管擁有更好的軸徑向彈性,有利于下錠膽系統的彈性減振;而另一方面又增大了彈性管的底部振幅。表明彈性管剛度和底部振幅 2個目標之間是相互制約的,因此,多目標優化模型以彈性管剛度和底部振幅為2個目標函數,從二者之間找到最優配置,達到既能降低彈性管剛度,增加彈性,又能保證其底部振幅較小的性能最優選擇。
2.2 優化問題數學模型構建
選取彈性管的主要影響參數槽寬c、螺距p、彈性模量E、壁厚h為設計變量,其中螺旋槽的槽寬取值范圍設定為0 ~ 2 mm;由于目前新型平錠底結構型錠子中心距和支承軸承尺寸的限制,螺距p取值范圍設定為6~12 mm;而壁厚取值范圍設定為1~4 mm;材料的彈性模量取值范圍設定為200 ~ 210 GPa;由于彈性管要承受自動落紗的軸向沖擊力,以及高速旋轉過程中的不平衡力對彈性管開螺旋槽部分的矩形彈簧造成剪切應力[5],剪切應力應滿足以下關系:
式中:τmax為最大軸向載荷下開螺旋槽部分矩形截面內側所產生的最大扭轉應力,N;p為螺距,mm;D0為彈簧中徑,mm;Fn為彈性管承受的軸向力,N;應力系數β2與矩形截面高寬比Φ(即(p-c)/h)和卷繞比D0/h有關,如表1所示;[τ]為許用剪切應力,視彈簧材料及受載情況而定。

表1 不同卷繞比下應力系數β2值Tab.1 Stress coefficient β2 at different winding ratios
2.3 優化流程
為以盡可能少的試驗次數得到有效的試驗數據來構建近似模型,采用試驗設計方法生成樣本點。首先,在MatLab仿真建模軟件中建立參數化數學模型,采用拉丁超立方設計方法生成設計變量樣本點后,調用數學模型進行數值分析,獲得離散的仿真值,然后結合近似模型技術,構建RBF近似模型,并檢驗近似模型精度。最后以抗彎剛度Jeq和底部振幅A最小為目標,在神經網絡模型上進行尋優,得到Pareto最優解集。
3 近似模型構建及優化研究
3.1 RBF神經網絡近似模型
近似模型方法是一種通過對具有代表性的局部點進行試驗,擬合局部范圍內因素與結果間的函數關系,取得各因素最優水平值的方法,適宜解決非線性數據處理的相關問題。常用的近似模型主要包括響應面法(RSM)、克里格模型(kriging)、神經網絡模型(RBF/EBF)等[6-7]。通過對優化目標構建幾種近似模型發現,RBF神經網絡近似模型能夠使優化目標近似精度達到可接受水平,其具有很強的逼近復雜非線性函數的能力和較強的容錯功能,即使樣本中含有“噪聲”輸入,也不影響模型的整體性能。
3.2 彈性管神經網絡模型構建
本文采用擬合平均相對誤差值E和復相關系數R2來衡量近似模型對試驗數據的擬合程度。平均相對誤差值E越小,代表可信度越高。R2值在0~1之間,如果R2值越接近1,則代表近似模型具有較高可信度[7]。通過拉丁超立方設計方法生成46個樣本點,采集到一組設計變量和目標值的樣本數據,進而構建神經網絡近似模型。圖3、4分別示出彈性管抗彎剛度Jeq及其底部振幅A的神經網絡模型。

圖3 彈性管抗彎剛度徑向基神經網絡模型Fig.3 Radial basis neural network model of elastic tube bending stiffness. (a) Approximate model of groove width and elastic modulus with bending stiffness; (b) Approximate model of pitch and wall thickness with bending stiffness
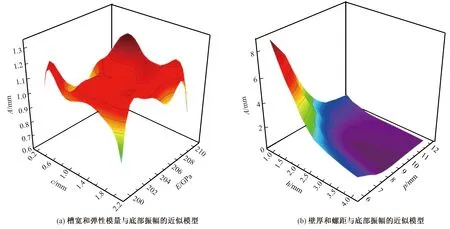
圖4 彈性管底部振幅徑向基神經網絡模型Fig.4 Radial-based neural network model of bottom of elastic tube. (a) Approximate model of groove width and elastic modulus with bottom amplitude; (b) Approximate model of pitch and wall thickness with bottom amplitude
為檢驗近似模型的精確度,采用隨機采樣方法在樣本空間重新取23個樣本點擬合平均相對誤差值E和復相關系數R2值。圖5、6示出剛度和振幅實際仿真與近似模型預測值擬合對比。其中對角線表示預測值等于仿真值,紅色點表示實際仿真樣本點,藍色水平線表示進行誤差分析的樣本點所對應響應的均值[8]。當實際仿真的樣本點落在與預測值相等的對角線上,且與對角線重合越緊密,就說明近似模型越可靠。結合平均相對誤差和R2值誤差檢驗結果(見表2)與圖5、6可知,該近似模型預測值可代替實際響應值,各目標值的平均相對誤差值和R2均達到可接受水平。說明神經網絡近似模型能滿足擬合精度要求。

圖5 剛度Jeq實際仿真值和近似模型預 測值擬合對比Fig.5 Comparison of actual simulation value of stiffness Jeq and approximate model prediction value

圖6 振幅A實際仿真值和近似模型預測值擬合對比Fig.6 Comparison of actual simulation value of amplitude A and approximate model prediction value

表2 平均相對誤差和R2值誤差檢驗Tab.2 Average relative error and R2 value error test
3.3 彈性管參數優化及多目標結果分析
多目標優化算法的類型很多,其中,NSGA-II 遺傳算法是在NSGA算法基礎上進行改進得到的,該算法導入了“擁擠距離”和“擁擠距離排序”,可使計算結果在目標空間內比較均勻地分布,保證種群的多樣性;還采用了精英策略將父代種群跟子代種群合并,保留父代優良個體,共同競爭產生下一代種群,防止Pareto最優解丟失[9-10]。
在多目標優化問題中,各目標響應值往往相互沖突,某個目標期望值的提高可能會引起其他目標值的降低,同時使多個目標達到最優一般是不可能的[11],因此,優化解不可能是單一的解,而是一個解集,稱為Pareto最優解集。Pareto最優解集在對應的目標函數空間的像稱為Pareto前沿。
在Isight平臺上將上述各響應值作為優化目標,對構建的減振彈性管近似模型進行多目標優化,優化算法選擇NSGA-Ⅱ遺傳算法,設置初始種群為20,遺傳代數為60,交叉率為0.9,計算消耗時間短,提高了計算效率,最終得到Pareto最優解集。
圖7示出對x、y軸取對數后的Jeq和A的Pareto前沿圖,黑色點表示可行解。可以看出,彈性管抗彎剛度Jeq和底部振幅A成反比關系,隨著抗彎剛度的增加,底部振幅逐漸減弱。

圖7 抗彎剛度Jeq和底部振幅A的Pareto前沿圖Fig.7 Pareto front of bending stiffness Jeq and amplitude A
雖然根據Pareto前沿圖分析了各目標之間的變化關系,得到了彈性管各性能指數之間的關系,但由于目標函數間是相互矛盾沖突的,無法衡量Pareto最優解之間的優劣。在實際設計時,設計者需要基于相關工況,對目標重要性進行權衡,選擇合適的最優解,最后通過實例驗證該方法的可行性,選擇合適的優化結果[12]。本文給出1組可行解作為優化算例,以此來體現優化結果的有效性。彈性管優化前后結果對比如表3所示。

表3 優化前后彈性管工藝參數對比Tab.3 Comparison before and after optimization of elastic pipe process parameters
由表3可知,優化后的2個目標值性能均有所改善,綜合分析可知,所選的可行解優化效果比較明顯。其中,抗彎剛度Jeq由0.46 N·m2增至 0.52 N·m2,部分提高了彈性管的剛度;在不平衡力作用下的底部振幅A由0.388 7 mm降低到了 0.119 9 mm。 此優化結果表明,在剛度僅增加13%的前提下,振幅就降低了69%,說明優化后錠子吸振彈性管在保持彈性的同時,高速旋轉下的穩定性也大幅提高。
通過仿真計算驗證了錠桿高速運行下傳遞給彈性管的激振力對其底部振幅的影響,如圖8所示。可以看出,優化后錠子在錠桿激振力作用下的彈性管底部振幅明顯減弱,隨著錠子高速旋轉過程中錠速的增加,錠子會伴隨著由之引起的不平衡力增加,而優化后的錠子彈性管底部振動相比優化前變化緩慢,說明優化后的錠子彈性管具有更加優良的性能,對吸振彈性管的高速下穩定性能有所提升。實驗驗證了優化方法的可行性和優越性,為錠子彈性管的結構設計提供了參數指導和優化方法的理論借鑒。

圖8 彈性管優化前后底部振幅的變化Fig.8 Variation of bottom amplitude before and after optimization of elastic tube
4 結 論
以彈性管結構起主要影響的參數槽寬、螺距、彈性模量、壁厚為設計變量,以彈性管抗彎剛度和底部振幅為目標函數,基于徑向基神經網絡(RBF)構建近似模型使其達到可接受水平,并結合遺傳算法對彈性管剛度及振動性能進行多目標優化設計,得到Pareto前沿提高了優化效率,通過得到的Pareto最優解集和Pareto前沿圖,分析得到1組可行的最優解,驗證此最優解發現,在彈性管剛度僅增加13%的前提下,振幅就降低了69%,說明優化后錠子吸振彈性管在保持彈性性能的同時,底部的振幅明顯減弱,錠子旋轉過程中傳遞的不平衡力引起的振動得到改善,使穩定性增加。

