超導電路與體聲波諧振器組成的量子iSWAP門方案
張凱旋,黃春暉,2
(1.福州大學 物理與信息工程學院,福建 福州 350116; 2.陽光學院 人工智能學院,福建 福州 350115)
0 引言
量子計算和量子通信已成為現代電子與信息技術的發展目標之一,實際上量子計算是由高精度的物理系統所實現,該系統的硬件部分一般由量子邏輯門和量子存儲器組成[1],用于控制高復雜度糾纏量子態的時間演化。基于超導約瑟夫森結的固體態量子系統具有較長的相干時間、易于制造和擴展量子比特(qubit)數目等特性,且可用制造現代集成電路的技術來制造該量子系統[2],是設計量子邏輯門和量子計算系統的一個強有力候選者。眾多量子門方案已在理論和實驗上得到研究,包括利用2個電容耦合[3]的電荷量子比特(charge qubit)和2個電感耦合[4]的磁通量子比特(flux qubit)。設計量子受控非門(C-NOT),尤其是高精度的兩位和三位量子門也已被實驗證實[5-6]。
與此同時,利用一維傳輸線諧振器耦合兩個charge qubit構造量子相位交換(iSWAP)門[7-8]和通過微納機械諧振器耦合charge qubit與flux qubit構造量子iSWAP門[9]同樣被證實。但僅簡單實現量子門功能是遠不能滿足量子計算的需求,實現高保真度量子門尤為重要。在已有報道中,具有高機械品質因數(Q>3 500[10])的薄膜體聲波諧振器(FBAR)耦合單個qubit的宏觀量子系統中,體聲波諧振器一般作為“冷卻器”,使系統的量子態穩定在基態[11-13],這為設計高保真度的量子門提供了新思路。因此,利用體聲波諧振器與超導量子電路構造的混合系統可實現高保真度的量子門。
此外,Cleland等[14]和Geller等[15]利用體聲波諧振器作為一個高保真度的量子存儲器和數據總線,在兩個或多個相位量子比特(phase qubit)間產生糾纏態和量子門,但因phase qubit的相干時間較短,在相干時間內量子門有效操縱次數較低。因此,本文提出了一個新穎的量子iSWAP門構建方案,通過體聲波諧振器耦合2個傳輸量子比特(transmon qubit),其中體聲波諧振器作為耦合器使transmon qubit間進行虛擬交互[7]。用體聲波諧振器的Butterworth-van Dyke模型[16]來理解與qubit間的耦合機制,簡化了設計體聲波諧振器物理參數的難度。此外,該諧振器可用制作約瑟夫森結的材料,如鋁、氮化鋁來制作,這種方案降低了制作量子iSWAP門的難度。同時,得益于trans-mon qubit較長的相干時間,在相干時間內本方案提高了有效執行iSWAP門操作的次數。
1 系統模型及其哈密頓量
圖1為本方案的電路模型。圖中,Φei(i=1, 2)為超導環內的磁通量,Φ0=h/(2e)為磁通量子,EJi(i=1, 2)為約瑟夫森能,ECi(i=1, 2)為約瑟夫森結的充電能,CTi為超導環的并聯電容。芯片1、2通過FBAR連接,其中芯片1、2由transmon qubit、外磁場驅動電路和測量電路組成,transmon qubit由2個相同的約瑟夫森結和超導環路并聯1個電容CTi(i=1,2是用于區分2個qubit及其相關參數)組成[17],穿過超導環內的外磁通量Φei用來調節qubit的躍遷頻率ωqi,transmon qubit的哈密頓量為
(1)
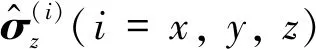
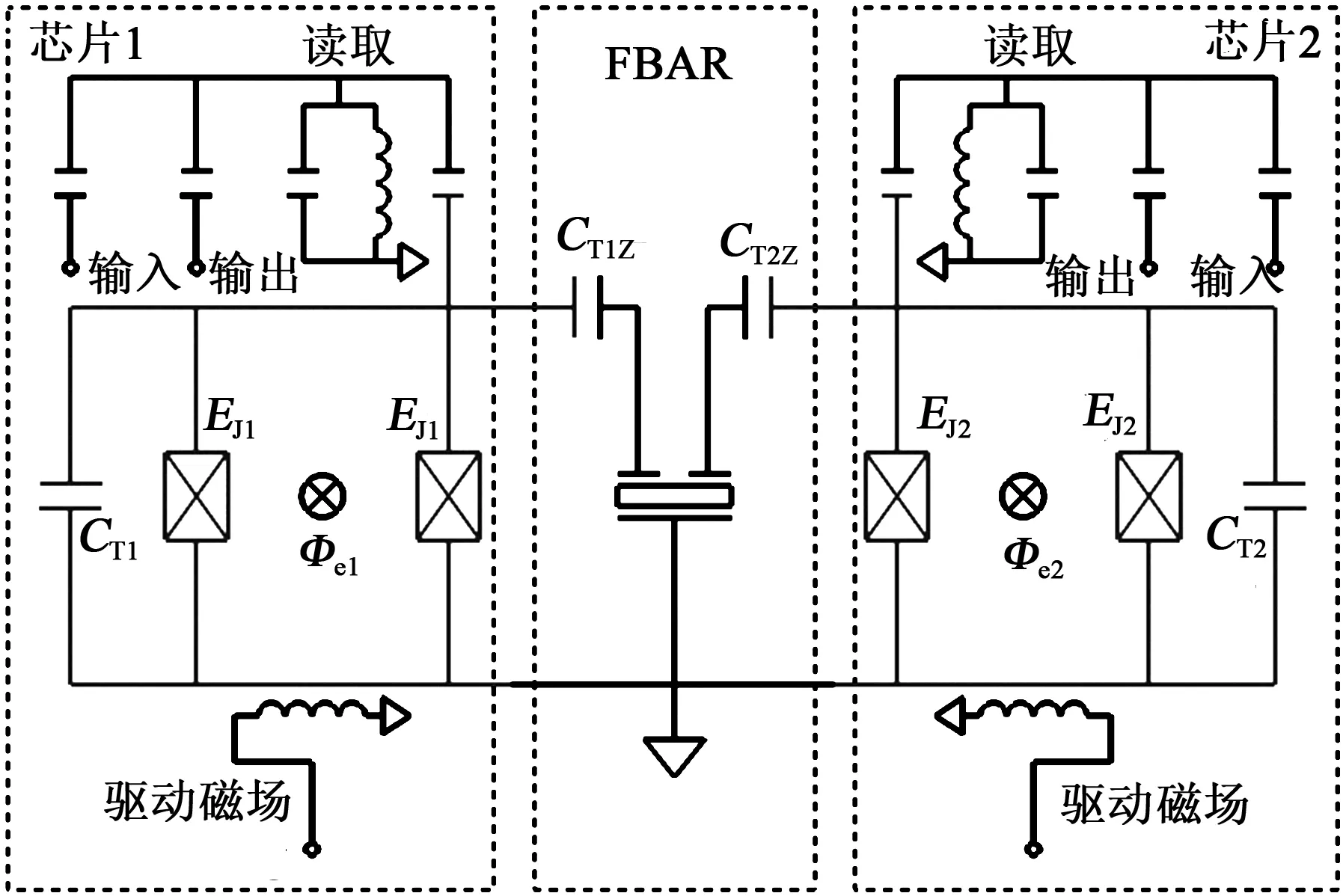
圖1 超導transmon qubit與FBAR混合量子門電路系統
理想的FBAR是由3個薄膜組成,本文采用Al/AlN/Al結構,即上、下層為Al電極層,中間壓電層選用具有強壓電效應的AlN,其中上電極層有寬度為w的縫隙,其作用是避免2個transmon qubit直接連接,且w取值足夠小時,不影響體聲波諧振器的功能。在1個振蕩周期中,AlN壓電層會隨著垂直方向的表面電荷變化而收縮和伸展,導致壓電層的厚度周期性變化如圖2(a)所示。反之,壓電層厚度的變化也會引起垂直方向的電荷變化。
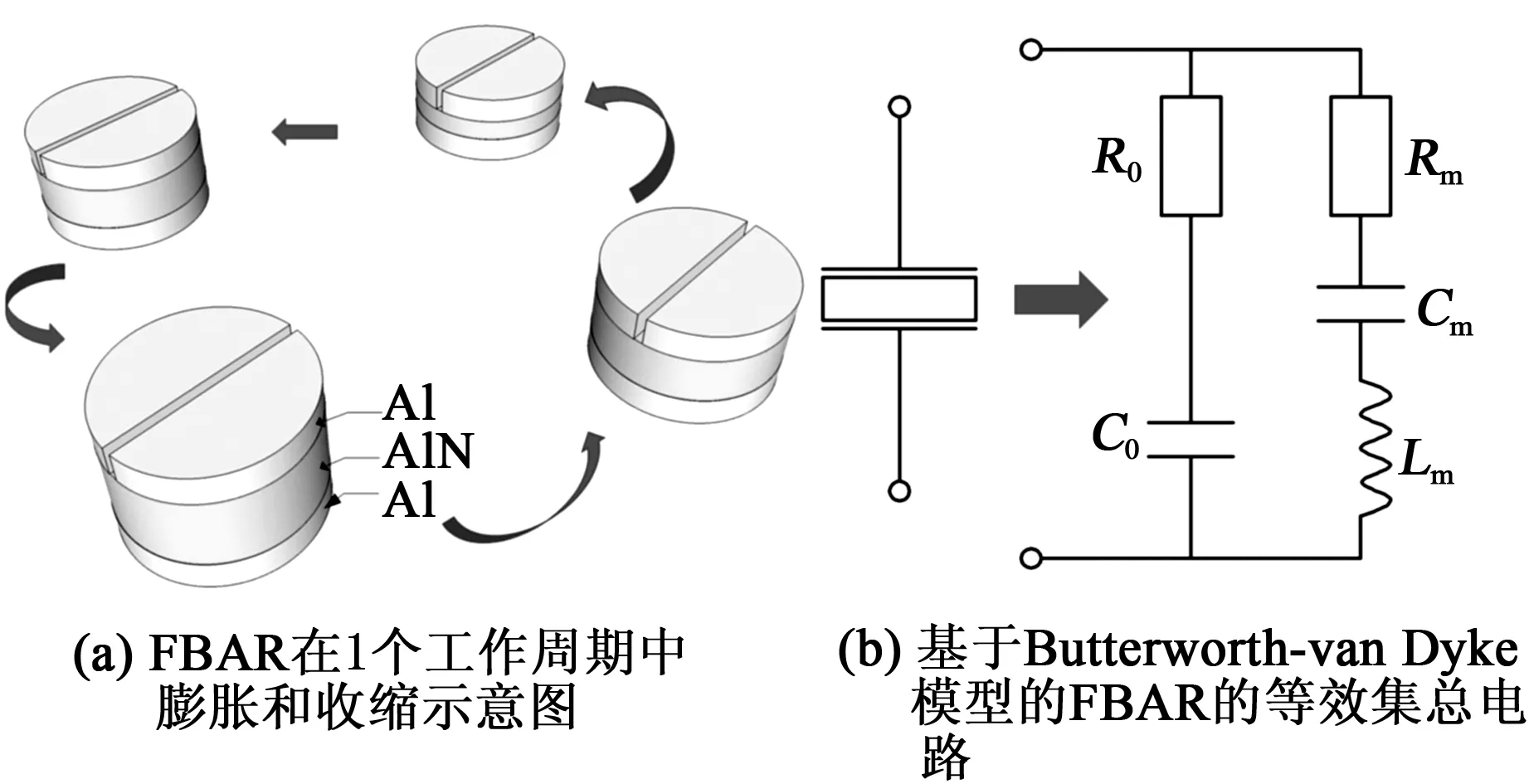
圖2 FBAR在1個工作周期中膨脹和收縮示意圖及基于Butterworth-van Dyke模型的FBAR的等效集總電路
用基于Butterworth-van Dyke模型的FBAR等效電路來闡述FBAR的工作機理,其等效電路如圖2(b)所示。圖中,R0為介電損耗,Cm為等效機械電容,Lm為等效機械電感,Rm為等效機械損耗,FBAR平行幾何電容C0=εrε0A/d(其中,εr為壓電層相對介電常數,ε0為真空介電常數,d為壓電層的厚度,A為電極層(Al)面積)。無量綱的壓電耦合系數為
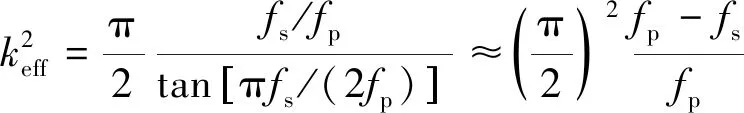
(2)
式中fs,fp分別為等效電路串、并聯諧振頻率,且
(3)
(4)
FBAR的哈密頓量為
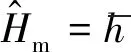
(5)
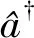
在系統中,FBAR作為耦合器連接2個qubit,類似微波光子通道的功能,使2個qubit間實現虛擬交互。在不考慮測量電路的影響時,本系統的哈密頓量為
(6)
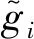
2 量子iSWAP門的實現
在式(6)的基礎上,調節系統外電源使qubit工作在簡并點處,利用旋波近似消除快速振蕩項,該混合系統的Jaynes-Cummings模型為
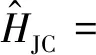
(7)
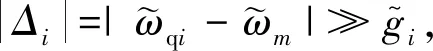
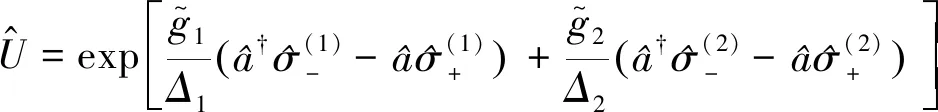
(8)
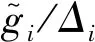
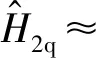
(9)
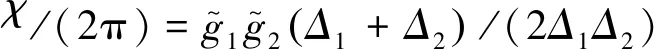
(10)
式中最后一項可以理解為qubit的態位能通過體聲波諧振器并暫時的存儲在諧振器中,之后該量子態位會通過FBAR以虛擬交互的方式傳送到其他的qubit。在旋轉坐標系下,該混合電路的時間演化算子為
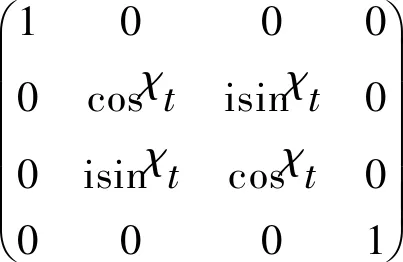
(11)
實際上,無論體聲波諧振器工作與否,熱激發引起體聲波諧振器激發到第一激發態的數量(單聲子)可表示為
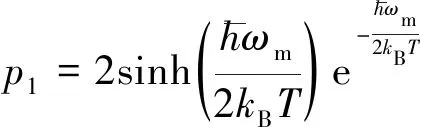
(12)
式中T為環境溫度。
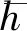
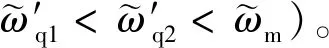
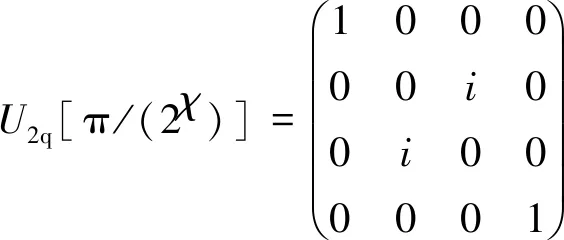
(13)
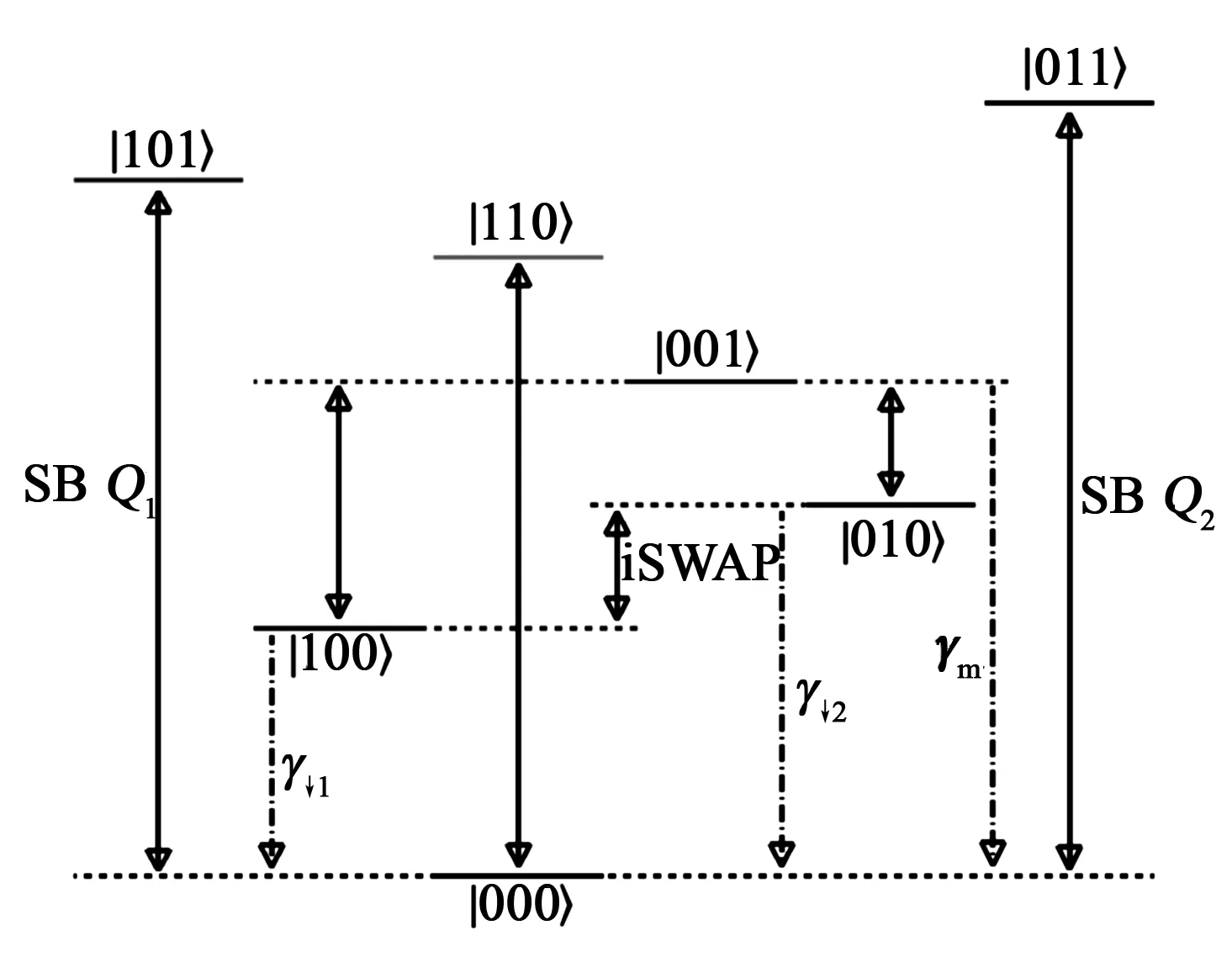
圖3 超導混合量子門系統的相對能級及其本征態之間的相干和退相干
在此基礎上,量子iSWAP門結合單qubit量子門能實現量子C-NOT門和高復雜的量子計算[19-20]。
3 系統參數設計及其數值仿真
下面介紹本系統的實驗可行性。為了獲得FBAR的fs、fp和機械品質因數Qm,從而獲得FBAR的等效電路參數,用有限元仿真軟件COMSOL Multiphysics 研究FBAR性質。FBAR的仿真模型如圖4(a)所示。
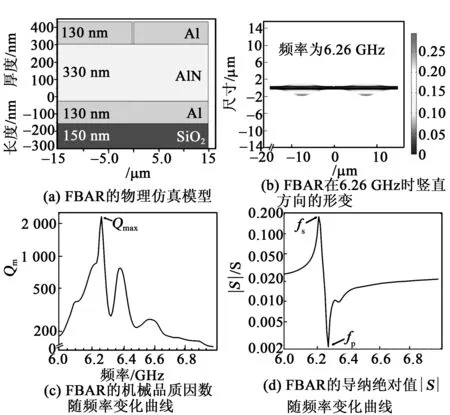
圖4 FBAR仿真模型及其仿真結果
SiO2襯底的縱向長為150 nm;Al電極層厚為130 nm,頂層的2個Al電極間縫隙為300 nm;AlN壓電層厚度d=330 nm。圖4(b)為仿真得到FBAR在特征頻率為6.26 GHz時的表面形變。由圖4(c)可看出,在特征頻率fmax=6.26 GHz時,FBAR的Qm達最大值為2 345.88。通過仿真結果結合式(1)可計算出FBAR等效電路的各個參數,如表1所示。

表1 FBAR的主要參數
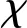
上述混合量子體系是理想情況下,但在實際實驗中,器件的耗散不可避免,這其中包括qubit的自身的弛豫和退相位、FBAR的耗散、超導環路的量子隧穿耗散。本系統中,起到主導影響的耗散是qubit自身退相位和FBAR的耗散,為了驗證本系統執行一次量子iSWAP門的可靠性,引入系統的主方程來驗證本器件的保真度,其主方程為
(14)
(15)
(16)
D[c]ρ=cρc?-c?cρ/2-ρc?c/2
(17)
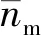
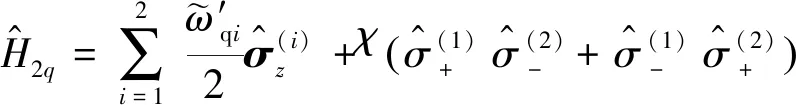
(18)
實施一次iSWAP操縱的過程層析(process tomography)如圖5所示(輸入態為|100〉),圖5為理想狀態和考慮系統散耗的過程層析仿真結果。其中,mn(m={i,x,y,z},n={i,x,y,z})為m和n的張量積。
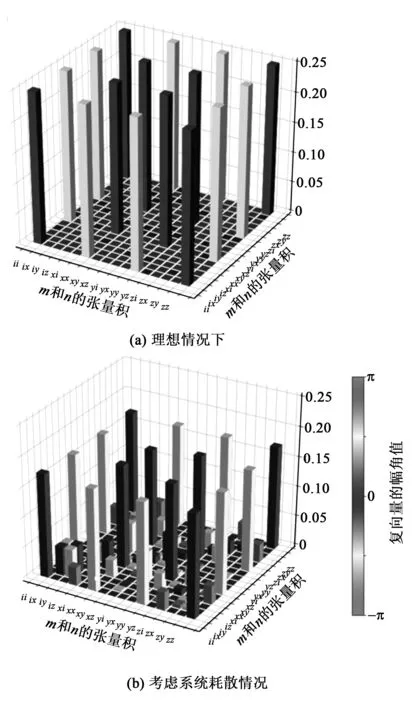
圖5 量子iSWAP門的過程層析
量子門的保真度是描述量子器件性能的一個重要指標,在仿真結果基礎上對本系統的保真度進行了分析。理想的量子iSWAP門,當輸入態為|100〉時,在tiSWAP后系統的輸出態為|010〉,其輸出態的密度矩陣ρI為
(19)
但在數值仿真時存在仿真誤差,數值仿真的輸出態密度矩陣為ρS,不考慮系統耗散時保真度為
(20)
由數值仿真結果可算出F=0.981 47。在考慮FBAR和qubit的耗散時,γm/(2π)≈4.201 MHz,γ↓i=0.01gi,γφi=0.001gi,數值仿真系統輸出態的密度矩陣為ρD,數值仿真保真度為
(21)
根據式(21)得到其保真度為0.968 15,表明了本系統在執行一次iSWAP邏輯操縱時具有較高的可靠度。
4 結束語
本文提出了超導量子電路與體聲波諧振器混合系統實現高保真度量子iSWAP門的新方案,引入體聲波諧振器的Butterworth-van Dyke模型,建立系統量子化的哈密頓量,體聲波諧振器起到類似微波光子通道的作用,使得兩個transmon qubit之間進行虛擬交互和量子態位傳送,并產生量子iSWAP邏輯功能。采用最新已報道的實驗數據,估算了體聲波諧振器和qubit的具體參數,數值仿真表明執行一次iSWAP操縱所需時間約為0.106 33 ms,且考慮系統耗散時其保真度高達0.968 15。該方案降低了制作超導量子門的難度,也為設計和制造高保真量子邏輯門奠定了基礎。

