斐索干涉儀中壓電陶瓷的非線性校正

王 芳，盧慶杰，韓 森,2

(1.上海理工大學 光電信息與計算機工程學院，上海 200093；2.蘇州慧利儀器有限責任公司，江蘇 蘇州 215123)

0 引言

目前，高精密元件和高性能光學系統(tǒng)在科學研究和生產工程領域發(fā)揮了重要作用，而先進的檢測技術和高端的檢測儀器對光學元件和光學系統(tǒng)的制造及使用尤為重要。光學干涉測量技術是現(xiàn)代最精密的測試技術之一，它能快速、準確地完成對光學元件面形與系統(tǒng)的檢測。相移干涉測量技術的基本概念是通過采集一組相移干涉圖，精確地提取干涉圖的相位[1-4]。壓電陶瓷(PZT)致動器相移法通常被使用，即利用PZT在電壓的驅動下產生位移形變的特性，使用其作為相移產生裝置。但由于PZT具有嚴重的遲滯非線性，直接導致相鄰幀干涉圖之間的相移量為非線性，從而提取的相位將攜帶誤差，影響著干涉儀的的測量結果。針對PZT的遲滯非線性問題，國內外學者已大量研究了遲滯模型(目前較成熟的模型主要有Preisach模型、Duhem模型及Maxwell模型等[5-11])及控制方法(主要有基于遲滯模型的前饋控制法、不基于遲滯模型的PID反饋控制法及前饋控制與反饋控制相結合的混合控制方法等[12-13])。

針對斐索干涉儀相移器的遲滯非線性特性，本文設計了一種基于PZT傳遞函數(shù)的前饋開環(huán)校正法的控制系統(tǒng)來校正PZT的遲滯非線性，該方法不存在反饋回路，簡單有效。整個控制系統(tǒng)包括電壓驅動系統(tǒng)和位移采集系統(tǒng)。PZT傳遞函數(shù)是通過PZT的輸入功能函數(shù)和輸出功能函數(shù)的關系來描述PZT的固有屬性，然后通過結合PZT的固有屬性及PZT的理想輸出位移可得到PZT理想的輸入電壓，最終完成PZT的非線性校正。

1 系統(tǒng)設計

1.1 相移誤差產生的相位誤差

根據(jù)雙光束干涉理論，干涉場中的光強分布[14]可表示為

I(x,y)=Idc(x,y)+Iac(x,y)cos[φ(x,y)+δn]

(n=-1,0,1,2,3)

(1)

式中：I(x,y)為測得的每幀干涉圖像的每個像素點的光強;Idc(x,y)為光強的偏移量;Iac(x,y)為調制光強峰谷值的一半;φ(x,y)為參考波前與被測波前的相位差;δn為相移量。

測量時可得到每幀干涉圖像每個像素點的光強。其中φ(x,y)，Idc(x,y),Iac(x,y)均是未知的，因此,至少需要3個干涉圖才能決定在不同圖像間的相位變化φ(x,y)。本文采用五步相移算法及相移量為π/2的方法來獲取φ(x,y),且

(2)

式中I1～I5為每步相移后測得的光強強度。

根據(jù)δn與PZT位移量ΔL之間的關系，則式(1)可表示為

I(x,y)=Idc(x,y)+Iac(x,y)·

(3)

由式(3)可知，PZT的非線性位移將導致非等步長的相移改變量，進而產生相位誤差。

相位誤差σφ可表示為

(A+B+C)

(4)

式中:λ=632.8 nm為激光干涉儀的波長；ΔL1,ΔL2,ΔL3,ΔL4,ΔL5為PZT每步的位移量。

(5)

(6)

(7)

根據(jù)以上分析，相位誤差可通過移相誤差求得,進而可求得被測表面形貌的高度(h)誤差及峰谷(PV)與起伏高度均方根誤差(RMS)，分別表示為

(8)

ΔPV=Δhmax-Δhmin

(9)

(10)

1.2 實驗系統(tǒng)

由于相位誤差引起高度(h)誤差，而相位誤差是由PZT移相誤差引起的，因此有必要提出一種控制系統(tǒng)和方法來校正PZT的遲滯非線性。實驗研究對象PZT作為斐索(Fizeau)干涉儀相移器的關鍵部件，推動參考鏡移動，進而產生光程差。圖1為斐索(Fizeau)型干涉儀的實驗平臺。

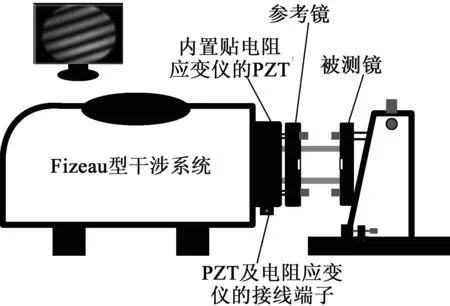
圖1 斐索型干涉儀實驗平臺

1.2.1 實驗裝置

圖2為實驗控制系統(tǒng)框圖。實驗系統(tǒng)采用矩形壓電陶瓷疊層致動器作為驅動源。該PZT內部集成了電阻應變儀，最大輸入電壓150 V,行程10 μm，電阻應變儀的固有阻值為1 kΩ。數(shù)據(jù)采集設備使用NI公司數(shù)據(jù)采集卡(PCIe-6321)和連接器(SCB-68A)，主要作用是與LabVIEW系統(tǒng)結合產生PZT的驅動電壓信號及與位移傳感器、LabVIEW系統(tǒng)結合獲取PZT的輸出位移。電壓放大器采用壓電控制器(XE-650.OA)，放大倍率為12.5，主要作用是放大PZT的驅動電壓信號。位移傳感器是一個單臂惠斯通橋式電路，其中內置于PZT的電阻應變儀為其中的1個臂，其余3個臂的阻值均為1 kΩ,電阻精度均為1%。位移傳感器采用5 V直流電壓供電，采用MATLAB軟件平臺設計前饋開環(huán)校正算法程序，對采集到的位移數(shù)據(jù)進行處理，最終求出PZT理想的驅動電壓值。

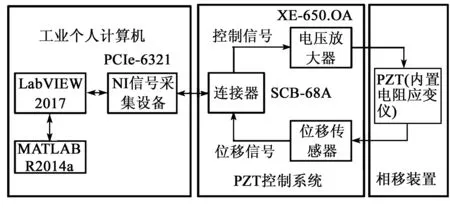
圖2 PZT控制系統(tǒng)

1.2.2 PZT位移非線性校正控制算法

為了補償PZT非線性特性產生的相位誤差，提出了一種前饋開環(huán)控制模型校正PZT的非線性特性,開環(huán)控制思想?yún)⒖嘉墨I[12],即將PZT的傳遞函數(shù)模型串聯(lián)在PZT之前，使PZT輸入與輸出呈線性關系。

輸入電壓Vin(t)是已知的PZT驅動電壓，根據(jù)干涉儀的測量要求，通過計算機、NI數(shù)據(jù)采集設備、LabVIEW系統(tǒng)及電壓放大器產生，Vin(t)可表示為

Vin(t)=kt

(11)

式中k為常數(shù)，根據(jù)干涉儀的測量要求設置k值。

當PZT被驅動后，可得其輸出位移Xout(t)，對Xout(t)信號進行多項式擬合處理，則

(12)

式中：p∈(0,P),P≥1；t∈(tm,tm+1),m=0,1,2，…；ap,P,tm，tm+1均為常數(shù)。

如果PZT的功能參數(shù)未知，則Vin(t)與Xout(t)間的關系為

Xout(t)=o(Vin(t))

(13)

式中ο為函數(shù)關系的表示符號。

同時理想的輸出位移可表示為

Xideal(t)=at+b

(14)

式中a，b是常數(shù)，且a，b根據(jù)干涉儀測量要求設定其數(shù)值。

針對同一個PZT，其新的理想輸入電壓Videal(t)與Xideal(t)間的關系可表示為

Xideal(t)=o(Videal(t))

(15)

根據(jù)式(13)～(15)可得：

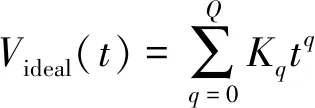
(16)

式中Kq,Q是常數(shù)，且Q>1。

1.3 實驗結果

1.3.1 線性校正PZT的位移

實際中，針對干涉儀利用五步相移算法對光學樣品進行表面三維形貌測量時，只使用到三角波驅動電壓的正向電壓驅動PZT推動參考鏡產生相移，所以，此實驗研究對象針對三角波驅動電壓的正向電壓，并對產生的位移進行線性校正。

在1.2節(jié)實驗系統(tǒng)的基礎上，系統(tǒng)產生幅值為100 V，頻率為0.5 Hz的周期三角波信號作為PZT的驅動電壓。系統(tǒng)的采樣速率為0.5 kSPS。在系統(tǒng)驅動PZT時，同步采集PZT的位移數(shù)據(jù)并存儲。取出PZT半個周期的位移增長數(shù)據(jù)，利用MATLAB軟件平臺以及1.2.2節(jié)介紹的開環(huán)控制算法，可得到PZT產生理想位移所需理想驅動電壓。然后將MATLAB計算出的驅動電壓值用來重新驅動PZT，系統(tǒng)再次采集PZT的位移數(shù)據(jù)，校正流程如圖3所示。圖4為PZT位移校正前、后的驅動電壓值。圖5為PZT校正前、后的位移值。

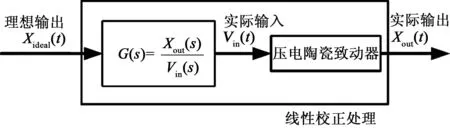
圖3 非線性校正控制算法框圖

圖4 PZT校正前、后的驅動電壓

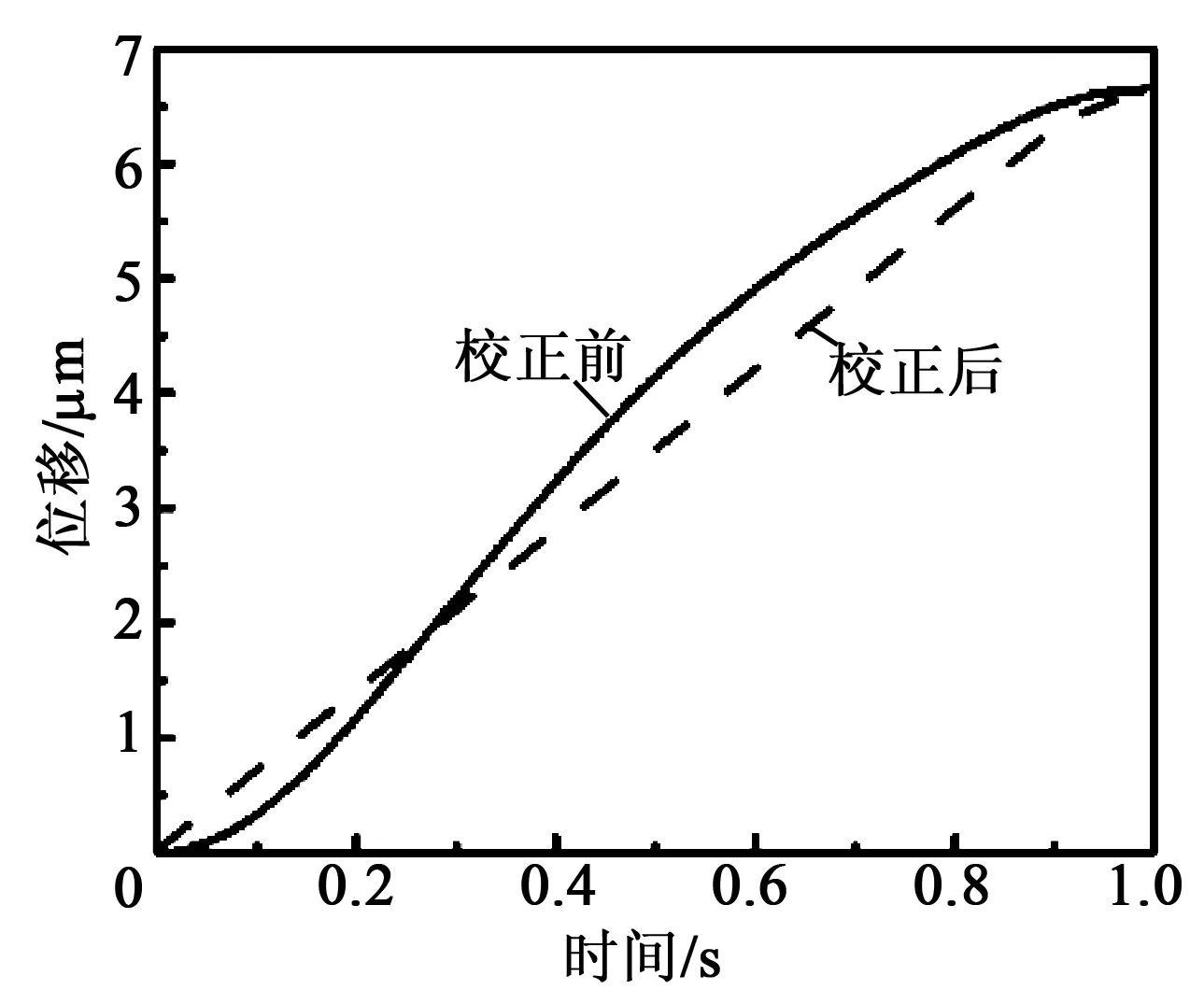
圖5 PZT校正前、后的位移

圖6為PZT校正前、后的驅動電壓差及位移差。由圖可看出，PZT校正前、后輸出與輸入函數(shù)呈反函數(shù)關系。

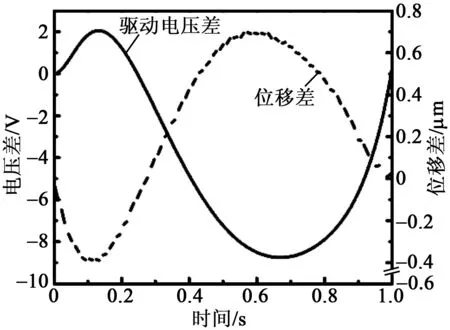
圖6 PZT校正前、后的驅動電壓差與位移差

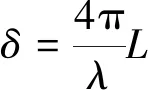
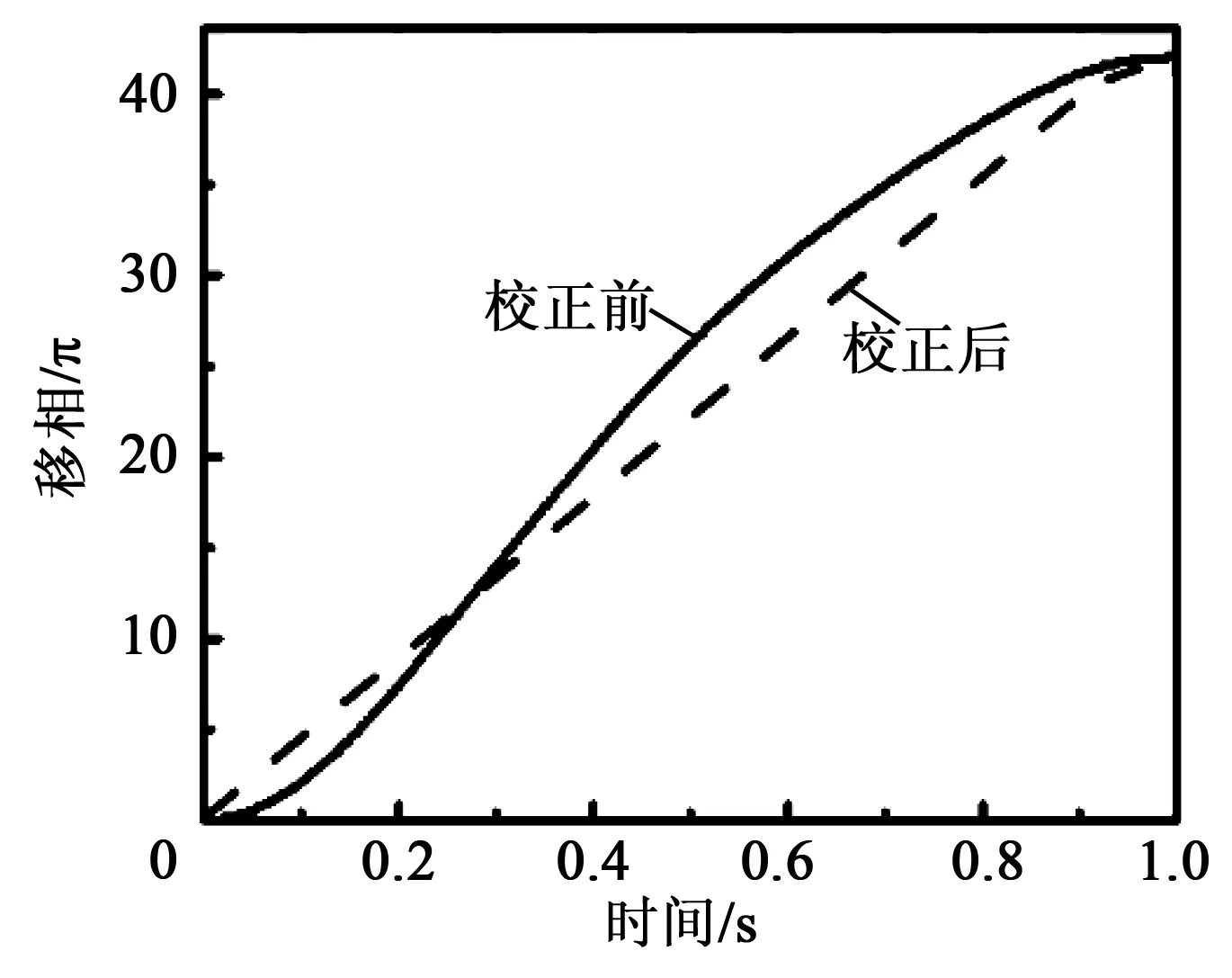
圖7 PZT校正前、后相移器的移相

1.3.2 相位誤差與高度誤差的模擬

圖8為PZT校正前、后系統(tǒng)的相位誤差。圖9為PZT校正前、后系統(tǒng)的高度誤差。校正前，MATLAB軟件編程產生32個相位值，以及5個相移誤差值，系統(tǒng)將會產生最大相位誤差為9.85×10-6rad，高度誤差為4.96×10-4nm。校正后，PZT的位移軌跡為線性，在相同時間間隔內可實現(xiàn)每步的相移量固定為π/2，相位誤差及高度誤差可被改善。

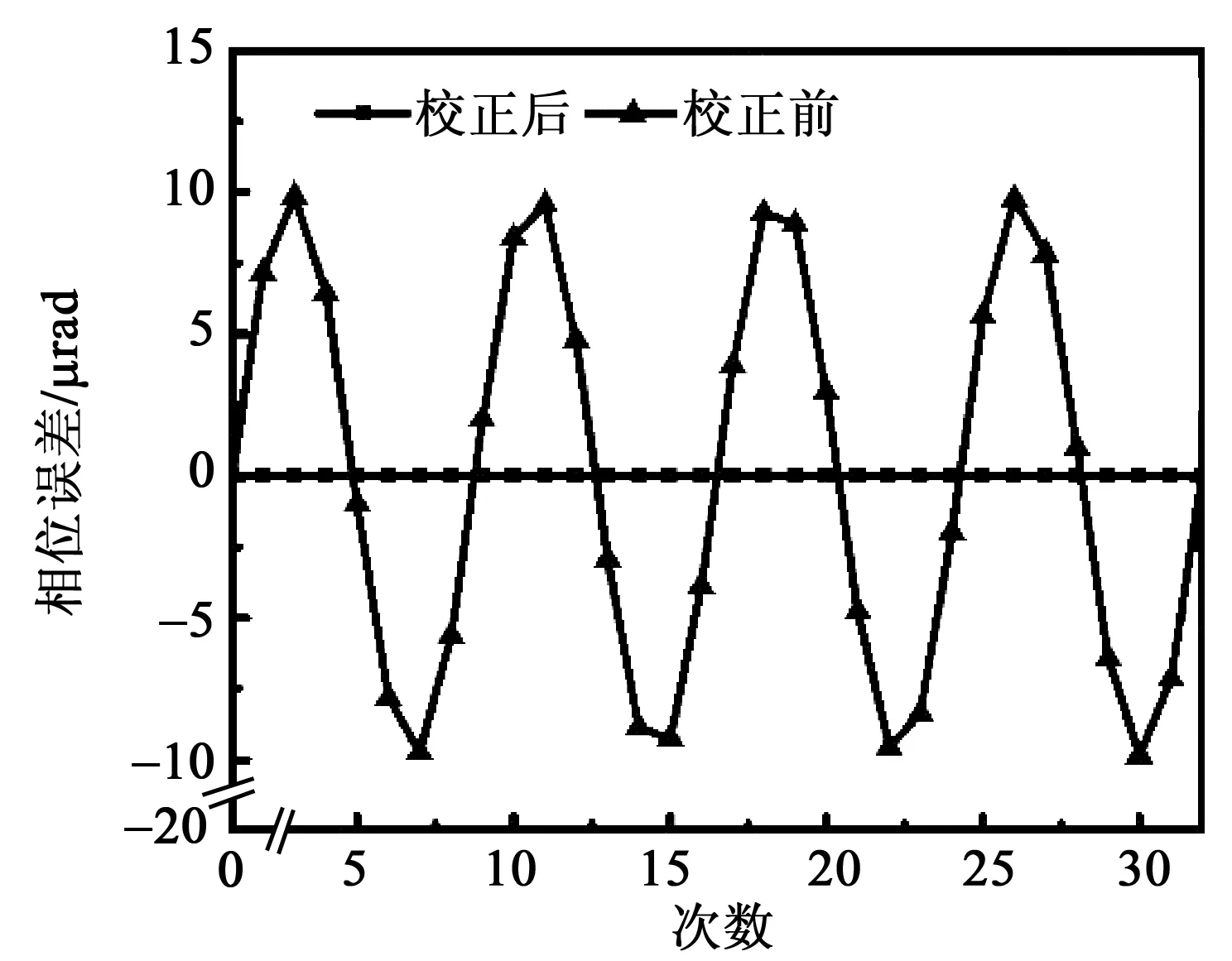
圖8 PZT校正前、后系統(tǒng)的相位誤差

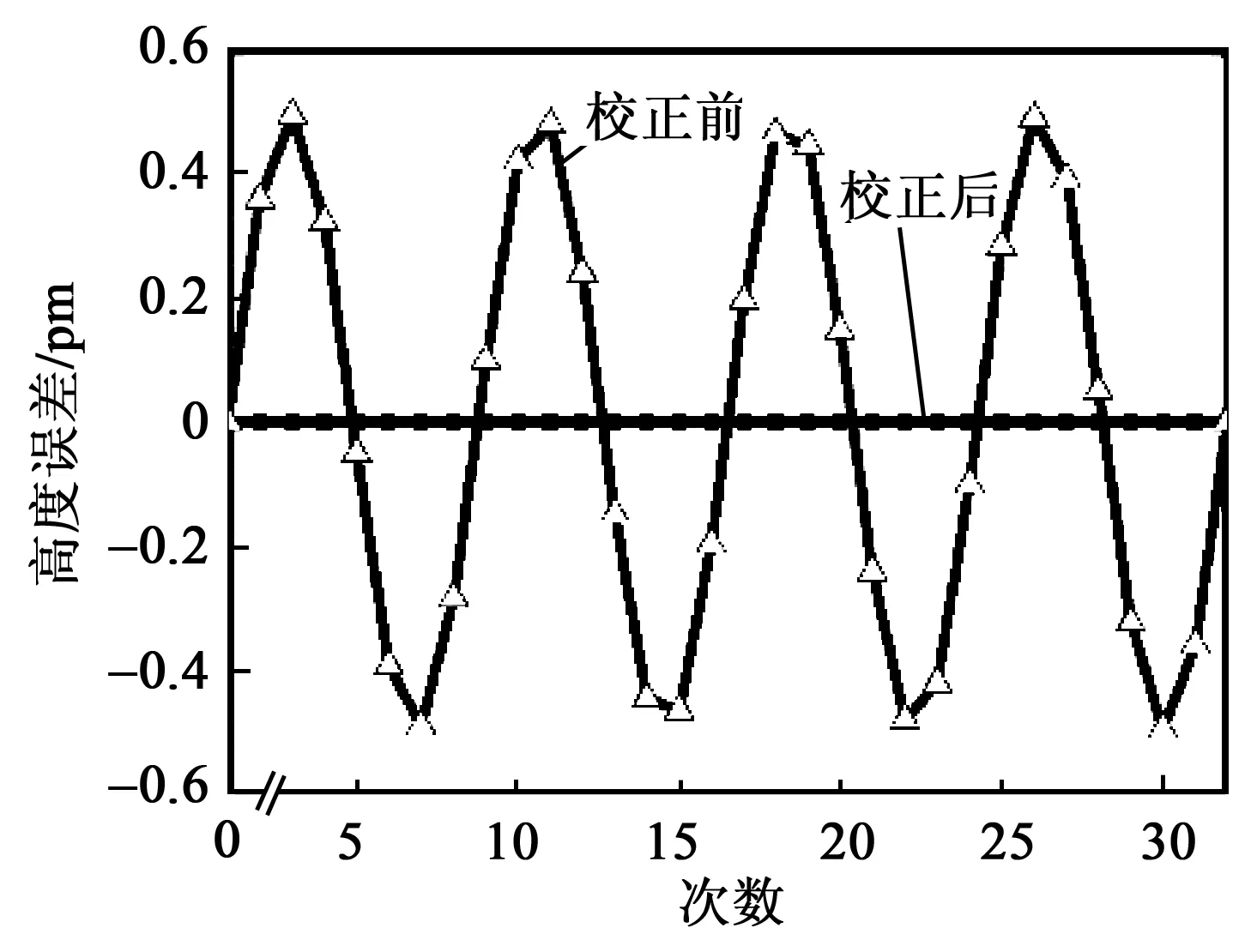
圖9 PZT校正前、后系統(tǒng)的高度誤差

2 結束語

本文結合斐索型干涉儀的實驗平臺，搭建了PZT相移器的控制系統(tǒng)，包括電壓驅動系統(tǒng)與位移采集系統(tǒng)。然后結合前饋開環(huán)控制算法，可有效完成PZT的遲滯非線性校正。實驗中，控制系統(tǒng)的采樣頻率為0.5 kSPS，輸入電壓頻率為0.5 Hz。校正前、后位移差小于10%。校正后，改善了移相誤差，同時改善了相位誤差和高度誤差，從而有效提高了干涉儀的測量精度。