微米級PZT驅動器尺度相關的自由振動分析

陳 明， 鄭世杰 ，田志昌，楊志軍，馮 鑫

(1.內蒙古科技大學 土木工程學院， 內蒙古 包頭 014010；2. 南京航天航空大學 機械結構力學及控制國家重點實驗室，江蘇 南京 210016)

0 引言

鋯鈦酸鉛(PbZrTiO3，PZT)壓電陶瓷擁有優良的壓電特性，廣泛應用于微機電系統中，結構的特征尺度達到微米量級。微納米結構力學行為的尺度相關性已在實驗室得到證實[1-2]。經典的連續介質理論不能準確描述微納米尺度構件的力學行為。

2002年，Yang等[3]在偶應力理論基礎上提出，修正偶應力理論僅包含一個尺度相關的材料內稟尺寸參數，被廣泛應用于分析微納米尺度力學結構。2011 年，Gao等[4]通過修正偶應力理論建立微米級Mindlin板模型，分析了簡支結構板的靜態彎曲和自由振動的尺寸相關性。2014年，Mesut等[5]將修正偶應力理論應用到非線性微米梁靜態撓度、固有頻率的尺寸效應分析。2015年，Mesut等[6]應用Kirchhoff-Love板理論結合修正偶應力理論分析了移動載荷作用下微米板的振動問題。除單一材料組成的微米梁板結構，在復合材料及功能梯度材料方面有較多研究開展。2011年，Chen等[7]基于修正偶應力理論，建立了考慮剪切變形的復合材料層合梁模型，分析模型的尺寸效應；并對比分析了歐拉-伯努利梁和鐵木辛柯梁的解。2011年，Ke等[8]運用鐵木辛柯梁理論結合修正偶應力理論分析了功能梯度梁動力學穩定性的尺寸效應。2015年，Li等[9]將修正偶應力理論應用于分析功能梯度壓電板的靜態彎曲和自由振動的尺寸相關性問題。2014年，Ansari等[10]在考慮電場引起應力變化情況下分析了微米級純壓電梁的振動特性。

上述研究主要集中在微米梁、板結構，關于壓電層合微米梁結構的研究較少。2016年，Zheng等[11]考慮力電的耦合作用，研究了對微米級PZT壓電層合驅動裝置的靜態力學行為進行了分析。本文在Zheng等[11]研究的基礎上，進一步對微米級PZT層合驅動裝置動態力學行為的尺寸效應進行分析。

1 微米級PZT驅動器的運動控制方程

PZT壓電驅動器由壓電片與基體組合而成。根據組合方式的不同可分為非均質和均質PZT雙晶片驅動器，如圖1所示。圖中，hp為PZT層厚度，he為金屬墊層厚度。

圖1 微米級PZT驅動器

下面根據修正偶應力理論和經典的層合梁理論，推導在力-電耦合作用下的微米PZT層合梁結構智能驅動器的運動控制方程。

修正偶應力理論本構關系[3]為

σij=λδijεkk+2μεij

(1)

mij=2l2μχij

(2)

幾何關系為

εij=(ui,j+uj,i)/2

(3)

(4)

(5)

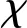
根據歐拉-伯努利梁理論，微米級PZT智能驅動器的本構方程如下：

對于PZT層有:

σx=Exεx-d31ExEz

(6)

(7)

Dz=d31σx+κ3Ez

(8)

對于基體彈性層有:

σx=Exεx

(9)

(10)

式中：Ex為材料的彈性模量；d31為材料的壓電常數；Ez為z方向電場強度；Dz為z方向電位移；κ3為介電常數。

非均質/均質PZT雙晶片驅動器在線彈性階段，電場與力場耦合下的總勢能為

(11)

式中V為體積。

假定梁結構在橫向分布力q(x,t)作用下，不考慮體力和體力偶的作用，則有

(12)

忽略軸向位移對動能(T)的影響，則T可表示為

(13)

式中：ρk為第k層梁的密度；Ak為第k層梁的橫截面積，k為驅動器層數。根據哈密頓原理有

(14)

將式(11)～(13)代入式(14)，得到微米級層合梁的運動控制方程：

q(x,t)

(15)

式中0

(16)

(17)

(18)

式中：D+R為彎曲剛度；Gk為第k層材料的剪切彈性模量。

若不考慮壓電效應，令hp=0，則式(15)、(16)與Kong等[12]給出的微米級歐拉-伯努利梁的振動控制方程一致。若令he=0，僅考慮單層壓電結構；同時，Ansari等[10]取壓電效應引起應力沿厚度均勻分布，并忽略泊松比影響，則與式(16)一致。

對于一端固定、一端自由，尺寸相關的非均質/均質PZT雙晶片驅動器，應用分離變量法，假設方程的通解為

w(x,t)=[C1sin(βx)+C2cos(βx)+

C3sinh(βx)+C4cosh(βx)]·

sin(ωt+φ)

(19)

根據式(19)可得頻率方程為

cos(βL)cosh(βL)=-1

(20)

式(20)的正根為βiL=1.875, 4.694, 7.855, 10.996, …, (i=1, 2, 3, 4, …)。

懸臂結構非均質/均質PZT雙晶片驅動器的自由振動方程為

[sin(βix)-sinh(βix)]}

(21)

對于非均質PZT雙晶片驅動器，固有頻率為

(22)

式中Ee、Ep、Ge、Gp分別表示彈性層和壓電層的彈性模量和剪切彈性模量;z0為中性層到底部壓電層中面的距離(見圖1)，且

(23)

(24)

(25)

若將尺寸參數設為0，則式(22)退化為經典懸臂結構非均質PZT雙晶片的固有頻率為

(26)

利用方程(22)、(26)，可得非均質PZT雙晶片歸一化固有頻率為

(27)

對于均質PZT雙晶片驅動器，固有頻率為

(28)

(29)

利用式(28)、(29)得到均質PZT雙晶片歸一化固有頻率為

(30)

2 算例分析

表1 PZT驅動器相關材料參數

圖3 不同基體厚度的非均質PZT雙晶片的

圖4 不同基體厚度均質PZT雙晶片的

圖5 不同基體材料均質PZT雙晶片的

3 結論

本文采用修正偶應力理論結合哈密頓原理，推導了微米尺度均質、非均質PZT雙晶片驅動器的運動控制方程和自由振動方程，給出了兩種結構的固有頻率。理論模型通過引入的內稟尺寸特征參數成功捕獲了微米尺度結構的尺度效應，并獲得模型隨結構尺寸、基體材料屬性等的變化規律，具體如下：

1) 不同基體材料對于均質/非均質PZT雙晶片驅動器歸一化固有頻率的影響有限，對均質PZT雙晶片驅動器的影響更明顯。

2) 隨著結構橫、縱向及厚度尺寸的增加，無論均質還是非均質PZT雙晶片驅動器，歸一化固有頻率均變小，并趨近于1；在結構特征尺寸達到尺寸參數5倍時，歸一化固有頻率接近1。

3) 隨著內稟尺寸特征參數增大，結構的抗彎剛度增加，歸一化固有頻率變大。