高速沖壓生產線上下料冗余機械臂的運動學分析

王凱強 ，于魯川 ，張建華 ，張志剛

（1.山東大學 機械工程學院，山東 濟南 250061；2.高效潔凈機械制造教育部重點實驗室/國家級機械基礎實驗教學示范中心，山東 濟南 250061；3.濟南二機床集團有限公司，山東 濟南 250022）

汽車產業的競爭日益激烈，汽車部件的生產效率對提高市場占有率具有十分重要的作用，而汽車車身超過60%的外覆蓋件部件是通過沖壓工藝生產制造，并且上下料系統是沖壓生產線最主要的單元，因此，提高上下料機械臂的運動節拍會極大提高汽車覆蓋件的生產效率。

通過機械臂在各個壓機之間進行物料輸送是目前應用最廣泛的上下料方式。上下料機械臂軌跡運動規劃的優劣直接決定著機械臂的運動節拍、工作效率、關節扭矩、整線配合等性能。將上下料機械臂設計成具有一定的冗余自由度可以提高其運行的靈活性，這種機械臂適合在高度受限的空間中工作，在運行平穩性、使用可靠性等方面要明顯優于冗余度低的機械臂[1]。高冗余機械臂可以處理一些非常規功能，但是運動學逆解求解困難，容易出現多解的情況，很多學者在求冗余機械的逆解方法上提供了有效的方法，Samer Yahya等人提出一種幾何方法，該方法能夠在無限解中運用較少的計算量來得出冗余或者超冗余機械臂的最佳解，這種方法適應性較強，可以適合所有的任意平面n序列機械臂[2]。García-Sedano等人[3]提出一種改進遺傳算法將機械臂的運行軌跡進行優化，生成無碰撞的有效的運行軌跡，最大程度的縮短運行周期的時間，此種方法考慮到了機械臂特定組件的幾何形狀，來調整路徑以優化給定沖壓單元中的循環時間。在軌跡規劃過程中還可以用五次均勻B樣條曲線對關鍵點進行擬合，并采用改進遺傳算法對擬合后的曲線進行尋優，然后求得曲線的速度、加速度曲線，通過此方法可以使運行軌跡更加平滑[4]。本文從建立機械臂的正運動學模型出發，對末端執行器軌跡和冗余自由度關節進行規劃，進而求出各關節的逆解，旨在對冗余機械臂的求逆解方法提供參考。

1 正運動學分析

1.1 模型分析

圖1為沖壓生產線上下料機械臂的三維模型，圖2為其結構簡圖，該機構共7個構件，8個低副，可以得出該送料臂的自由度為5，由于其運動全部是在一個平面中運行，所以此機械臂具有兩個冗余的自由度。

1.2 正運動學求解

圖2中各符號表示的意義為：S為參考坐標系，T為工具坐標系。d0表示各關節角度為0時，滑塊D1理論最低點和參考坐標系S原點的距離，d10表滑塊D1初始位置和D1理論最低點之間的距離，d1為滑塊D1的位移，r2為連桿 R2的長度，r31表示滑塊D7的關節點和大擺臂與R2連點之間的距離，d40為滑塊D4初始位置距離滑塊D7之間的距離，d4為滑塊D4的位移，r5為送料臂R5的長度，R6為末端執行器。

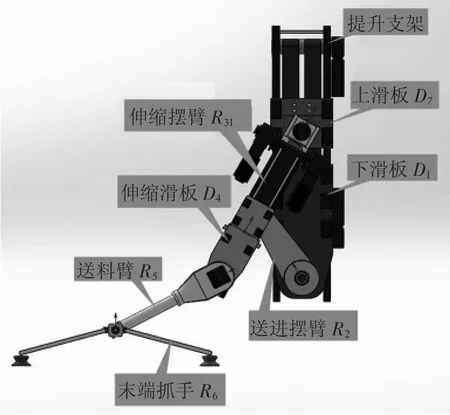
圖1 送料臂三維模型

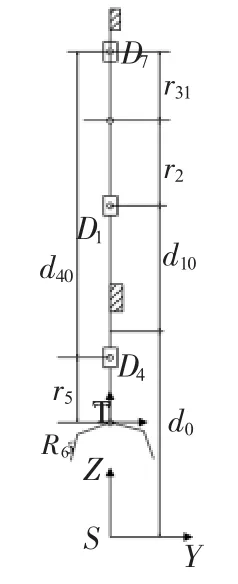
圖2 送料臂簡圖

根據對上下料機械臂的結構分析可知：滑塊D7屬于從動件，其運動軌跡可根據其他關節的軌跡確定，在進行運行學求解時不需要對其求解。旋量理論在正運動學建模中相對于D-H法具有簡潔、幾何關系明顯的優點，只需要建立參考坐標系S和工具坐標系T，不需要在各關節軸上建立局部坐標系，計算過程也比較簡單。

應用旋量理論將參考坐標系S的原點建立在地面和機械臂中軸線的交點，工具坐標系T建立在末端執行器R6的旋轉關節處，當上下料機械臂各個關節角為0時參考坐標系和工具坐標系的坐標轉換關系為：

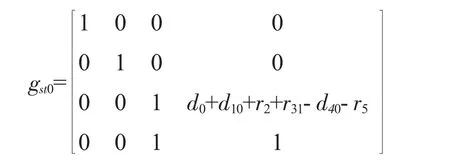
通過分析機械臂的結構可知所有的旋轉運動只繞著旋轉軸線的轉動而沒有沿軸線的移動，其節距為0，各關節軸線的單位矢量分別為：

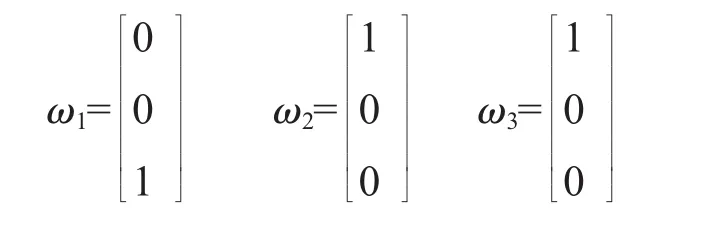
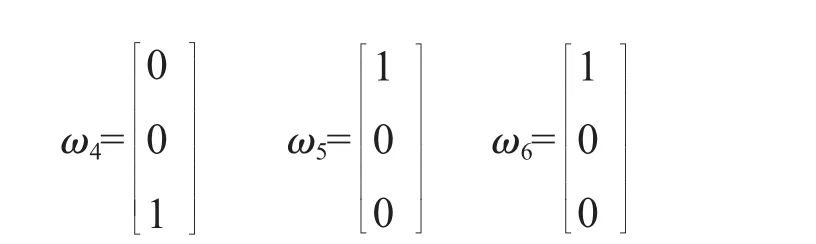
各旋轉關節軸線在各關節角為0時經過的點分為：

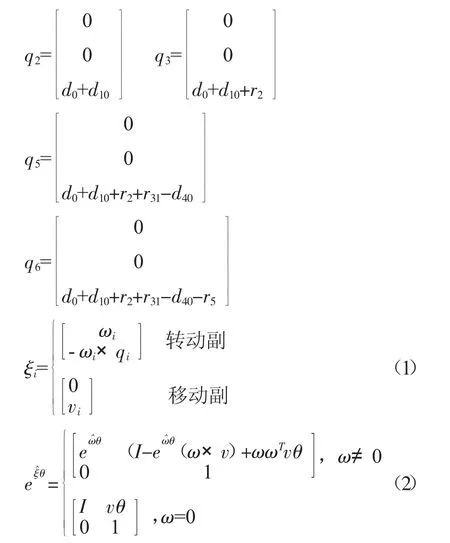
根據旋量理論，關節的運動副旋量計算公式（1）和指數積公式（2）可以得出各關節的指數積公式為：

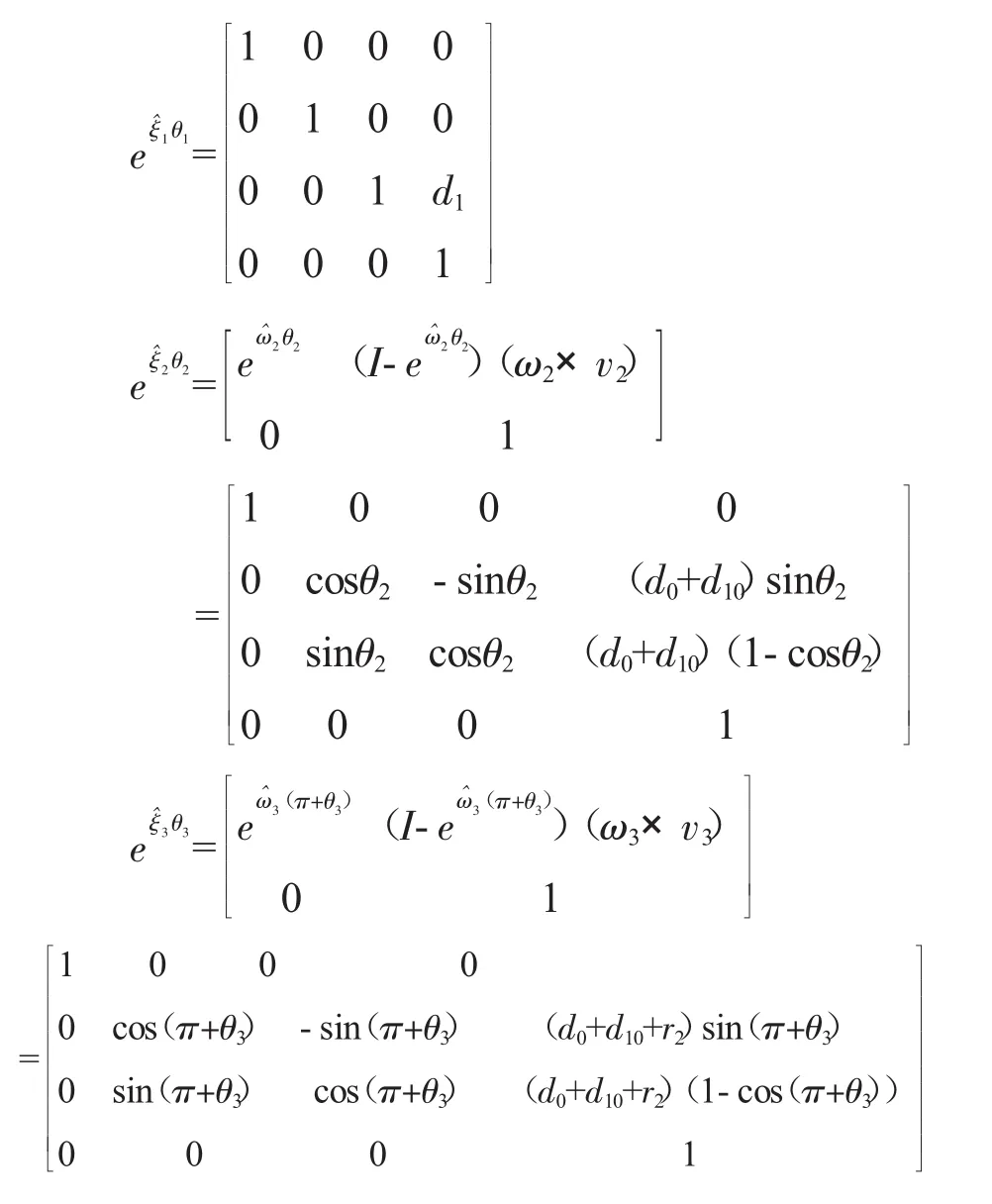
θ3的初始位姿為180°，其角度變化要添加一個相位角，所以其角度為（π+θ3）。

機械臂的正運動學方程可以通過各關節的指數積矩陣相乘得到：

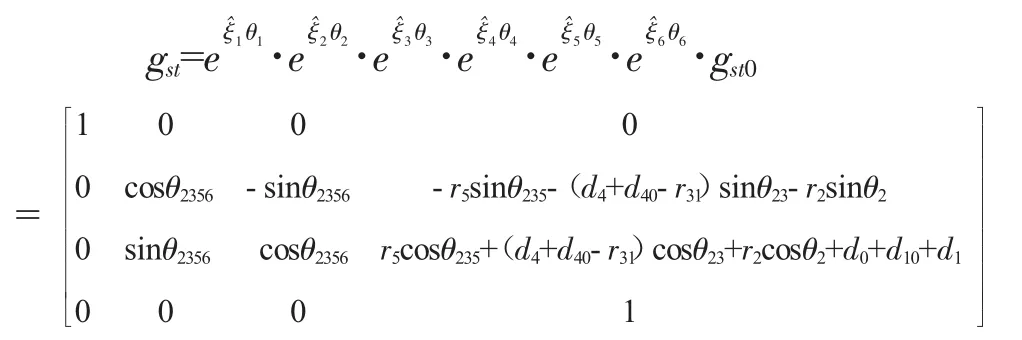
在正運動學方程中，角度和位移都為矢量，在進行指數積方程運算時不需要考慮其正負，在求解時若符號為正則旋轉軸的運動方向表示為在右手坐標系中，沿軸線方向觀察為順時針方向，對于移動軸移動方向為沿Z軸正方向運。其各簡化符號的意義為：

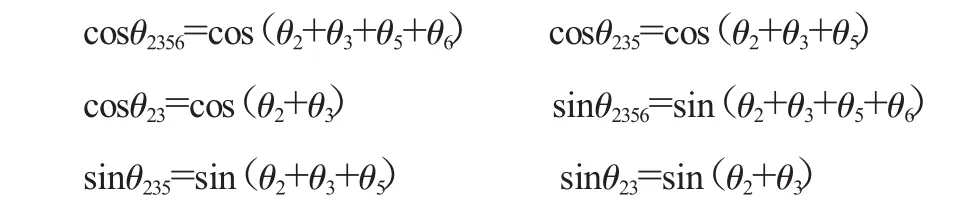
2 逆運動學求解

2.1 末端執行器軌跡規劃

在機械臂的軌跡規劃過程中，連接起點和終點位姿的具有時間序列的點或者曲線叫做軌跡，用多項式或者樣條曲線對曲線關鍵點進行擬合稱為軌跡規劃[5，6]，用算法將規劃后的軌跡進行優化叫做軌跡優化[7]。

在進行末端執行器軌跡進行規劃前，需要對其關鍵點進行設定。送料機械臂末端執行器的運行參數如表1所示，關鍵點主要設置在Home點和模區邊界、取放料點。關鍵點的選取將直接決定末端執行器運行時的速度、加速度、沖擊、關節扭矩等。而其非關鍵點的位置可以在一定范圍內波動，這就能夠提供一定的優化空間。

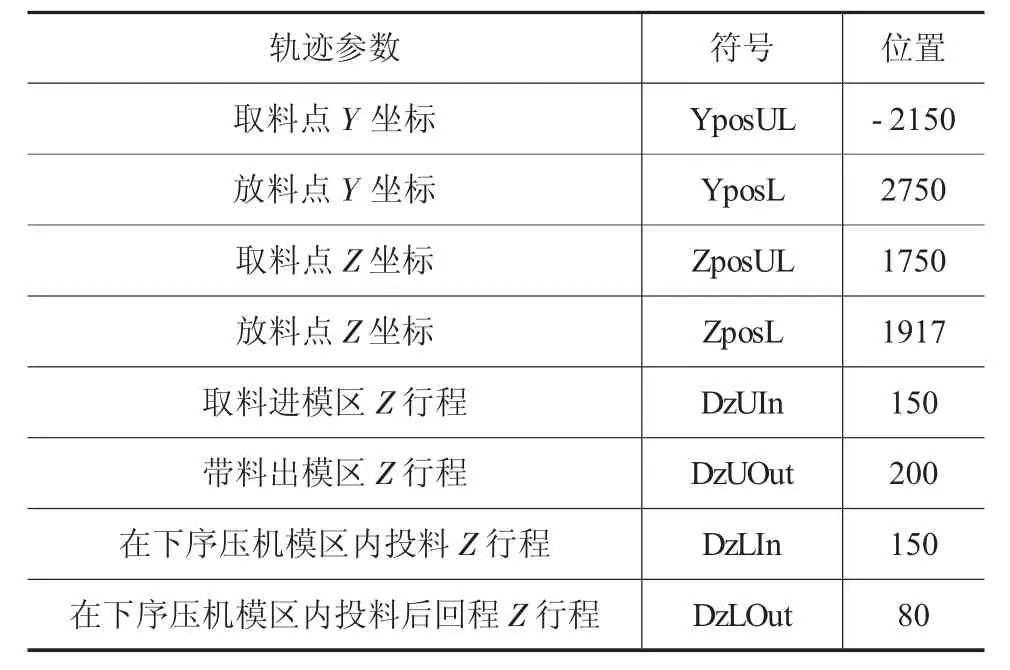
表1 機械臂末端執行器運行參數

B樣條是一種以“逼近”為原理的擬合曲線[8]，根據表1中末端執行器Y方向和Z方向的運行參數可以對其進行初步的規劃，通過在MATLAB中設定關鍵點采用五次B樣條曲線的插值方式形成初步的位移曲線，這樣可以保證擬合后的軌跡曲線的位移、速度、加速度都連續可導，使運行軌跡盡可能的平滑。在機械臂初始運行時選取幾個點為靜點，這樣可以避免運行過程中出現加速度突變或加速度無限大的情況。

沖擊率的定義為加速度相對于時間的變化率，稱之為加加速度[9]。為保證采用五次B樣條差值的位移曲線的沖擊率盡可能的小，可采用算法對其進行優化，使軌跡更加平滑。遺傳算法作為一種通用的智能算法，可以將目標函數進行迭代尋優，最終得到最優解。以加加速度的最大值為優化目標，通過調節非關鍵點處對應的時間使其最大值盡量減少，經過編碼、計算適應度值、選擇、交叉、變異的操作，迭代次數設定為50代，最終得出沖擊率最小的一條曲線。末端執行器Y方向和Z方向運行軌跡的位移、速度、加速度優化前和優化后的圖像如圖3、圖4所示，加加速度優化前和優化后的圖像如圖5、圖6所示。

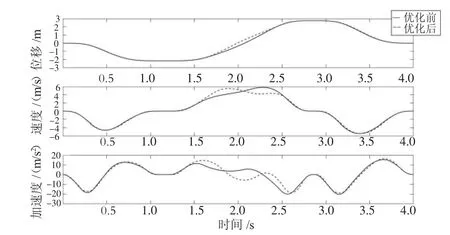
圖3 末端執行器Y方向位移、速度、加速度優化前和優化后對比

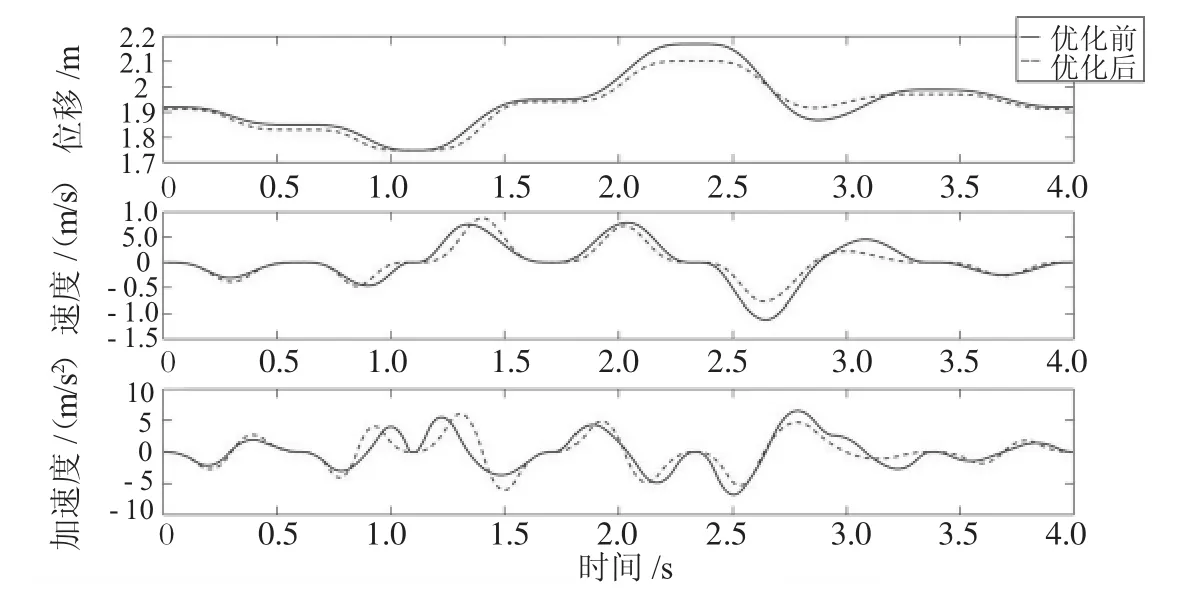
圖4 末端執行器Z方向位移、速度、加速度優化前和優化后對比

從圖3和圖4可以看出，加加速度的調整導致了位移曲線的變化，使運行軌跡在某些非關鍵點處發生了變化。從圖5和圖6中可以看出：末端執行器Y方向和Z方向軌跡的加加速度波動范圍變小，在絕對值最大處經過優化后明顯降低，表明遺傳算法的優化效果使沖擊率變化更加穩定。

在Matlab中進行優化的過程中，記錄每代種群二次加速度的最大值，加加速度的最大值隨迭代次數的變化趨勢如圖7和圖8所示。

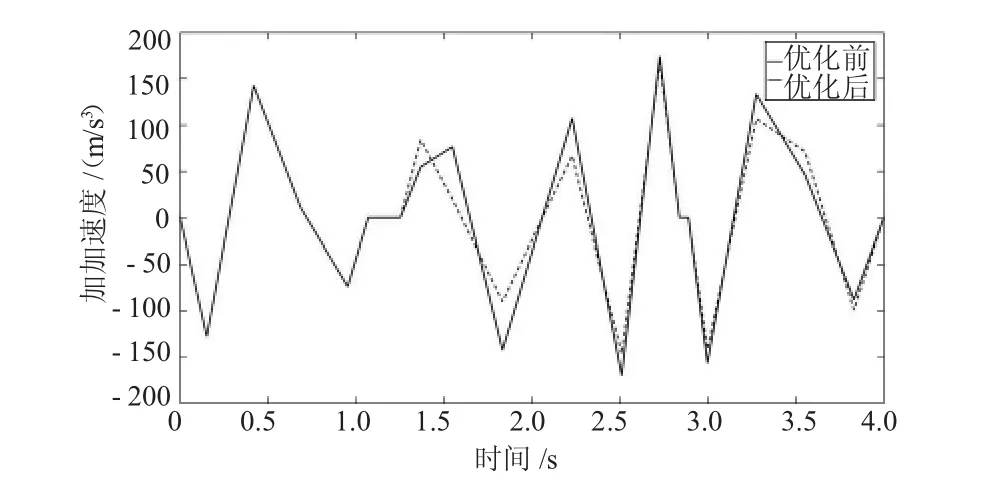
圖5 末端執行器Y方向加加速度優化前和優化后對比

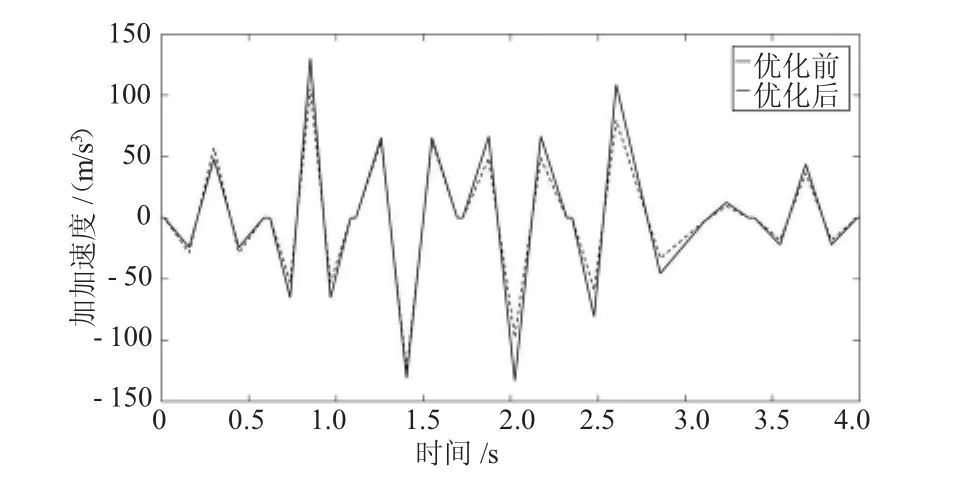
圖6 末端執行器Z方向加加速度優化前和優化后對比

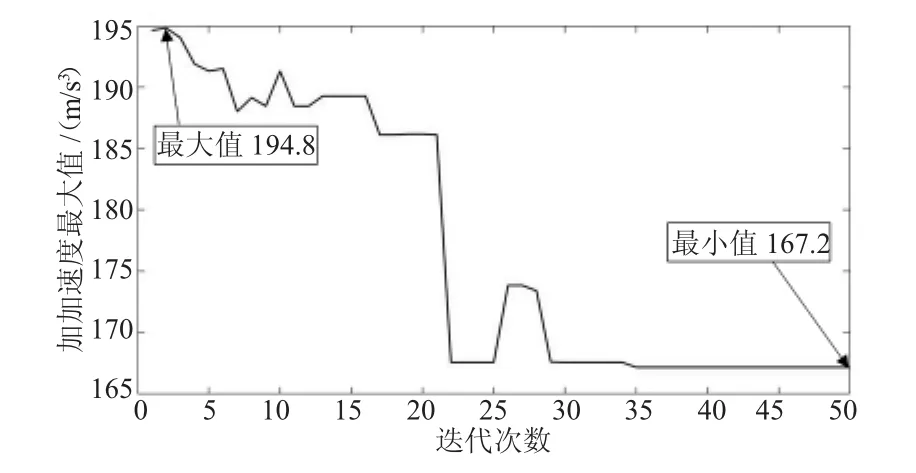
圖7 末端執行器Y方向加加速度最大值變化趨勢

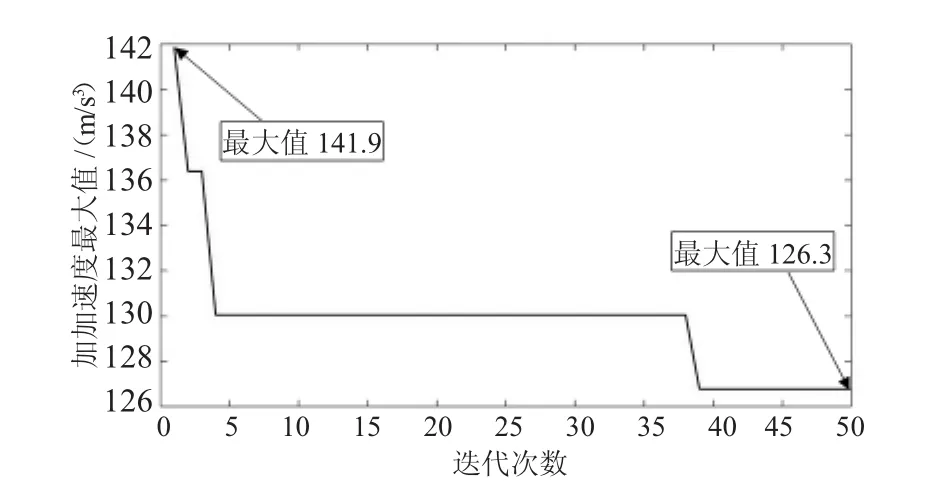
圖8 末端執行器Z軸加加速度最大值變化趨勢

從圖7和圖8中可以看出，Y方向和Z方向加加速度的最大值隨著迭代次數的增加呈減小趨勢，分別在第35代和40代左右達到穩定狀態，加加速度最大值分別減小了14.2%和11.0%，說明遺傳算法沒有提前收斂且優化效果比較明顯。

2.2 冗余關節的軌跡規劃

前面提到此送料機械臂的自由度為5，有兩個冗余自由度，如果直接求運動學逆解，會導致多解或者無解的情況發生。采用消除冗余自由度的方法可以解決這一問題。在選擇消除的冗余自由度時，各個關節都可以作為對象，各關節的求解效率會根據選擇消除自由度的關節的不同差別很大。經過多次測試發現對滑塊D4和R5_R6關節進行規劃，可以大大提高其他關節的求解效率。在對滑塊D4和R5_R6關節進行規劃時采用的方法和末端執行器的方法一樣，固定關鍵位置點然后采用五次B樣條曲線進行擬合，擬合后的運動曲線如圖9和圖10所示。

2.3 其他關節求解

根據正運動學方程和機械臂的幾何關系可得：

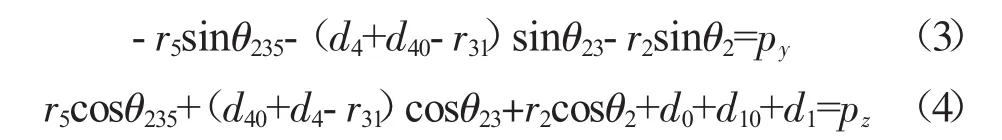
根據 θ2，θ3，r2，r31之間的三角幾何關系，并根據正弦定理可得：

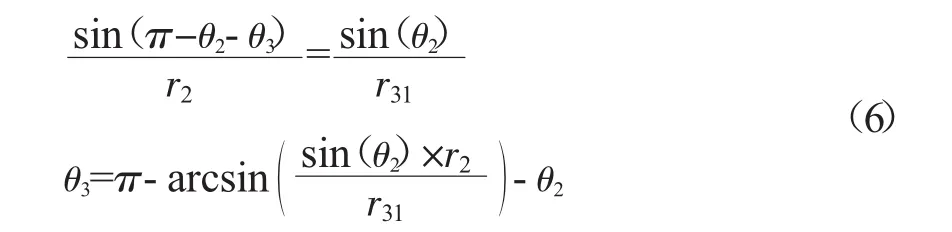
圖9 滑塊D1位移、速度、加速度、加加速度曲線

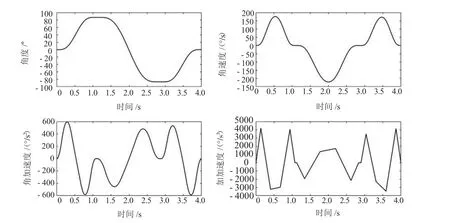
圖10 R5_R6關節位移、速度、加速度、加加速度曲線

式（3）、（4）、（5）、（6）中 py，pz，d4，θ6已經通過軌跡規劃求出，四個方程四個未知量，可以求出唯一的解。利用MATLAB的數值計算功能對其他關節進行求解，求解結果如圖11～圖14所示。

通過圖11～圖14可以看出求出的其他關節解的運動曲線是連續并且比較平滑，各關節運動過程比較平穩，沒有較大的波動，說明前面的軌跡規劃和優化效果比較明顯。

3 結論

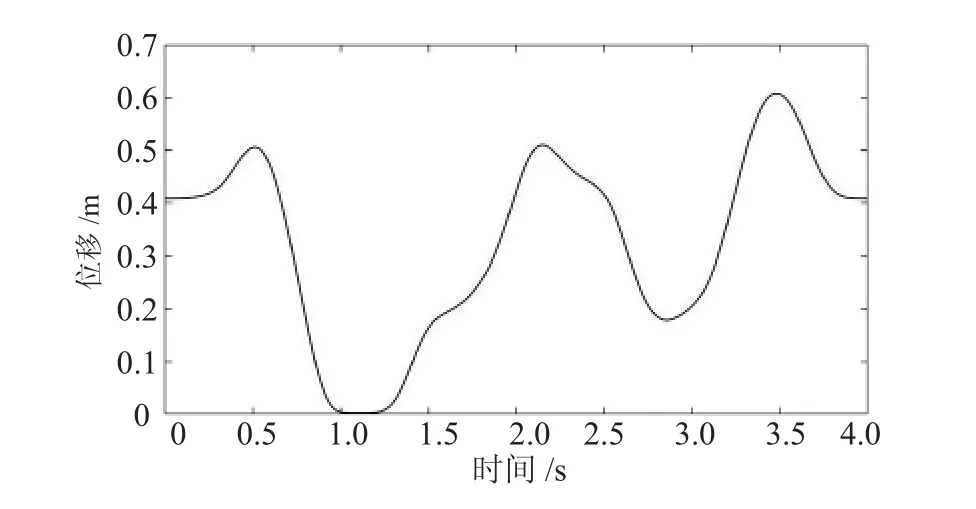
圖11 移動滑塊D1位移曲線

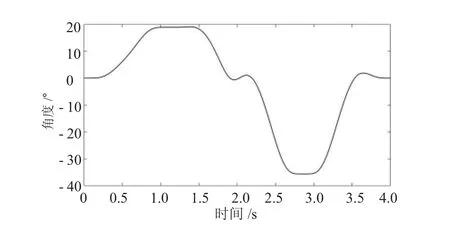
圖12 轉動關節D1_R2角度曲線

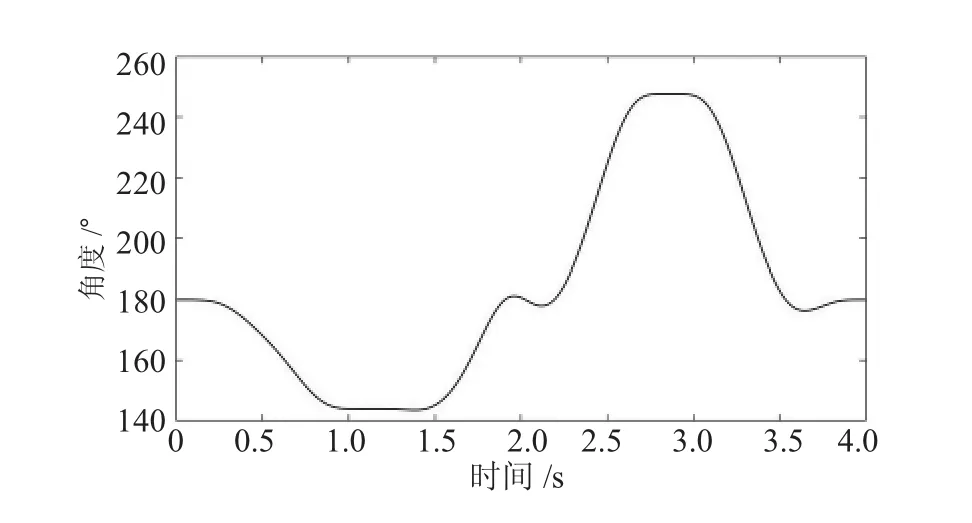
圖13 轉動關節R2_R31角度曲線

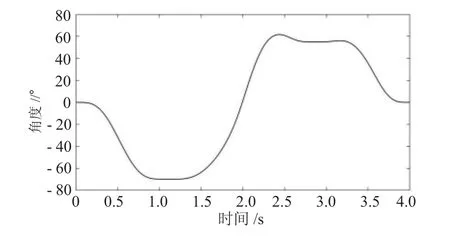
圖14 轉動關節D4_R5角度曲線

軌跡規劃在沖壓生產線的上下料系統中發揮著至關重要的作用，本文根據上下料機械臂的工作過程和冗余機械臂特點提出一種通用的運動學分析方法，主要工作有以下兩點：

（1）采用五次B樣條曲線結合遺傳算法對末端執行器的運行軌跡進行規劃和優化，使運行軌跡更加平滑，能夠將最大沖擊率降低10%以上，從而可提高上下料機械臂的平穩性。

（2）針對冗余機械臂的求逆解特點，選擇首先對滑塊D1和R5_R6關節的軌跡進行規劃，提高其他關節的求解效率。