基于巖性及結構特征的砂巖含水層富水性評價

魏久傳，趙智超，謝道雷，俞功一山，吳 霞

(1.山東科技大學 地球科學與工程學院，山東 青島 266590； 2.山東省煤田地質局 物探測量隊，山東 濟南 250104)

礦井水害是煤礦安全生產(chǎn)的重大威脅，其中煤層頂板砂巖水害是重要災害類型之一。在我國各時代煤田中，可采煤層頂、底板往往廣泛分布著砂巖含水層。在礦井建設和煤炭資源開采過程中，若井巷工程揭露或溝通砂巖含水層富水區(qū)域，可瞬間引發(fā)大量突水，輕者造成淹面淹頭事故，重者可引發(fā)淹井甚至慘重的人員傷亡事故[1-2]。

在傳統(tǒng)研究中，砂巖含水層富水性評價通常建立在大量物探、鉆探、水文地質試驗(抽水試驗、放水試驗等)基礎之上。然而，在實際生產(chǎn)中，抽水鉆孔數(shù)量一般較少，且控制范圍有限，無法滿足對含水層富水性分布規(guī)律的詳細控制；物探方法如瞬變電磁法、直流電法等[3]存在工作量大、費用高等問題，且物探資料的多解性使得對富水區(qū)的解譯成為難題，常出現(xiàn)謬誤。因此，借助大量現(xiàn)有地質勘查鉆孔資料，充分利用數(shù)據(jù)綜合分析方法，提取煤層頂板巖性特征及分布規(guī)律等信息，分析含水層富水性，是一種簡便有效的方法。我國相關領域專家學者對含水層富水性的研究，主要通過對多指標求得權重來構建富水性模型，如：武強等[4]選取含水層厚度、脆塑性巖厚度比、單位涌水量、巖石質量指標、滲透系數(shù)、沖洗液消耗量、斷層、陷落柱、褶皺樞紐軸等9個指標，運用層次分析法確定權重構建富水性評價模型；武旭仁等[5]運用模糊聚類分析法構建含有砂巖厚度、砂泥比和斷層維數(shù)3個指標的評價體系；李哲等[6]選取含水層厚度、巖芯采取率、脆性巖厚度、風化影響指數(shù)作為評價指標，應用人工神經(jīng)網(wǎng)絡得出富水性評價模型。數(shù)據(jù)綜合分析法中關于權重的確定常選取單一方法，其中主觀賦權法重視各指標本身的含義，可以體現(xiàn)決策者對不同指標的重視程度，但客觀性較差；而客觀賦權法具有較強的數(shù)學理論依據(jù)，但缺少決策者的參與和對實際情況的考慮。

本研究結合典型實例，遵循客觀科學性、全面性、定量與定性分析相結合的原則，運用熵權系數(shù)法、主成分分析法和層次分析法，選取砂巖等效厚度等多個評價指標，確定綜合權重并構建預測模型，對砂巖含水層的富水性進行預測分區(qū)，為防治頂板水害提供依據(jù)。

1 研究區(qū)概況

研究區(qū)位于內蒙古自治區(qū)鄂爾多斯市西南部的烏審旗境內(圖1)，內部構造活動較為微弱，構造不發(fā)育，含煤地層為侏羅系中下統(tǒng)延安組，討論的22采區(qū)2煤層可采厚度5.86～8.03 m，平均厚度6.88 m。2煤上覆直羅組砂巖含水層、安定組隔水層和志丹群砂巖含水層，含隔水層結構如圖2所示。安定組發(fā)育多層泥巖、砂質泥巖、粉砂巖等，其巖性較致密，透水性能差，為相對隔水層。因此，2煤頂板直羅組砂巖含水層、志丹群砂巖含水層為影響2煤開采的主要含水層。

2 含水層富水性因素分析

2.1 富水因素的確定

研究區(qū)營盤壕煤礦處于鄂爾多斯盆地中部，內部構造活動較弱，構造不發(fā)育，沉積環(huán)境是控制該地區(qū)地層中含(隔)水層空間分布與含水層富水規(guī)律的主要因素，因此在指標的選取中主要考慮巖性對富水性的影響。選取砂巖等效厚度(M)、砂巖巖性系數(shù)(S)、巖芯采取率(P)、砂泥巖層比率(Q)4個因素作為研究區(qū)富水性分區(qū)評價指標，對煤層頂板砂巖含水層的富水性做出預測。

圖1 研究區(qū)位置示意圖

圖2 含、隔水層結構示意圖

1) 砂巖等效厚度(M)

砂巖厚度作為含水層富水性評價的主要指標之一[7-8]，其厚度越大富水性越強。然而在已有的富水性評價研究中，砂巖厚度往往僅將含水層內不同砂巖厚度簡單相加，而忽略了粗、中、細砂巖的孔隙度及滲透性差異，結果往往與實際有較大出入。本研究引入砂巖的等效厚度(M)，將砂巖孔隙度比值作為不同砂巖厚度換算的比例系數(shù)，乘以各類砂巖的真實厚度得到砂巖等效厚度，具體公式為：

M=M粗+k1M中+k2M細，

(1)

其中：M粗、M中、M細分別為粗砂巖、中砂巖、細砂巖的真實厚度，m；k1為中砂巖厚度換算等效系數(shù)；k2為細砂巖厚度換算等效系數(shù)。

本研究按照覆壓下巖石孔隙度和滲透率測定方法(SY/T 6385—1999)標準對研究區(qū)直羅組不同層段巖芯進行了測試(表1)，并以粗砂巖為基礎(設定為1)，折算中、細砂巖對粗砂巖厚度換算的等效系數(shù)。結果顯示k1=0.8，k2=0.7。

表1 2煤頂板直羅組巖層孔隙度統(tǒng)計分析表

2) 砂巖巖性系數(shù)(S)

砂巖巖性系數(shù)(S)是砂巖的實際厚度與研究范圍直羅組厚度的比值，該比值越大，說明該段巖層中砂巖占比越高，富水性越強。

3) 巖芯采取率(P)

巖層的孔隙、裂隙為地下水的賦存提供了重要空間，選取巖芯采取率(P)能夠直觀地反映巖體完整程度，了解裂隙發(fā)育程度。巖芯采取率越高，說明巖層越完整，其中裂隙發(fā)育的就越少，富水性就越弱，故巖芯采取率和富水性成負相關。

4) 砂泥巖層比率(Q)

砂-泥巖的組合特征直接影響含水層的滲透性，砂泥互層越多，隔水性能越好，然而，單層砂巖或者泥巖厚度也對富水性有顯著影響，為克服這一局限性，提出砂泥巖層比率這一評價指標，即一定巖層厚度范圍內，砂質巖層和泥質巖層的總層數(shù)與該組地層厚度的比值，本文將每10 m巖層中的砂泥互層數(shù)定義為砂泥巖層比率，該值越大，表明隔水能力越強，富水性越弱。

2.2 數(shù)據(jù)標準化

文中確定的影響含水層富水性的指標具有不同的量綱，為了使數(shù)據(jù)之間具有可比性和客觀性，對原始數(shù)據(jù)進行標準化處理，采用的極差標準化公式為：

(2)

其中：X為該指標原始數(shù)值；Xmax、Xmin分別為該指標原始數(shù)據(jù)中的最大、最小值，Xi為該指標標準化結果值。

原始數(shù)據(jù)經(jīng)過標準化后的結果見表2。各指標標準化后單因素專題圖如圖3所示。

表2 直羅組含水層富水性各影響因素數(shù)據(jù)標準化值匯總表

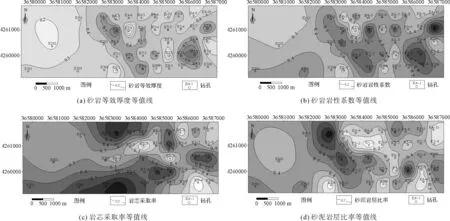
圖3 直羅組含水層富水性評價單因素評價專題圖

3 評價指標權重確定

熵權系數(shù)法確定權系數(shù)具有客觀性強、數(shù)學理論完善等優(yōu)點，但評價指標之間可能存在一定的相關性；主成分分析能夠有效消除樣本中冗余的信息，但在變量降維的過程中不得不付出使變量帶有模糊性的代價；層次分析法能夠將對象視作一個系統(tǒng)，使定性與定量相結合，可以將專家針對不同開采地質條件下的分析經(jīng)驗應用到評價中。三種方法的結合，可以減少單一評價方法對某一指標權重的絕對影響，削弱或消除單一方法的弊端。經(jīng)試算比較，將三種計算方法相結合能夠提高計算結果的準確度。

3.1 熵權系數(shù)法確定權重

熵權系數(shù)法(entropy weight method，EWM)的基本思路是根據(jù)指標變異性的大小來確定客觀權重，熵值越小，變異程度越大，權重也就越大[9]。具體步驟如下：

1) 求各指標的信息熵

根據(jù)信息論中信息熵的定義，一組數(shù)據(jù)的熵值為

(3)

其中

(4)

2) 確定各指標權重

根據(jù)信息熵的計算公式，計算出各個指標的信息熵為H1,H2,…,Hm。通過信息熵計算各指標的權重：

(5)

計算4個評價指標M、S、P、Q的權重并進行歸一化處理，得到權重結果分別為0.353 4、0.258 3、0.022 1、0.366 2。

3.2 主成分分析法確定權重

主成分分析法(principal component analysis，PCA)是將原有變量重新組合生成少數(shù)幾個彼此不相關的變量即主成分，使它們盡可能多地提取原有變量的信息[10-11]。通常做線性組合使原變量重新組合成主成分：

(6)

其中：a1i，a2i，…，api(i=1，2，…，m)為X的協(xié)方差陣特征值對應的特征向量；X1，X2，…，Xp是原始數(shù)據(jù)經(jīng)過標準化的值。

評價因子的權重，數(shù)學表達式如式(7)所示。

(7)

其中，gq為第q主成分的方差貢獻率，aqi(q=1,2,…,m;)為i因子在q主成分中的系數(shù)，所求的wi為第i個指標的權重值。

利用SPSS軟件對數(shù)據(jù)進行分析，結果見表3和表4。

按照主成分特征值大于1選取成分1(F1)和成分2(F2)兩個主成分，其累積貢獻率分別是50.887%，83.770%(表3)。

表3 主成分貢獻率與累積貢獻率 Tab. 3 Principal component contribution rate and cumulative contribution rate

表4 成份得分系數(shù)矩陣

根據(jù)表3和式(6)得到主成分表達式：

F1=0.470M+0.475S-0.151P+0.150Q，

(8)

F2=0.047M-0.059S+0.626P+0.601Q。

(9)

根據(jù)式(7)，主成分所求權重w1=|0.470×50.887%+0.047×32.884%|=0.254 6，同理可得w2=0.222 3,w3=0.129 0,w4=0.274 0。歸一化后得4個評價指標M、S、P、Q的權重分別為0.289 4、0.252 7、0.146 6、0.311 4。

3.3 層次分析法確定權重

層次分析法(analytic hierarchy process，AHP)，是一種定量和定性相結合將決策問題分解為多準則、多目標、多指標的實用決策方法[12-14]。本研究借助專業(yè)層次分析軟件yaahp確定各個影響指標的權重。

1) 建立層次結構模型

將決策目標、中間層要素、備選方案繪制層次結構圖如圖4。

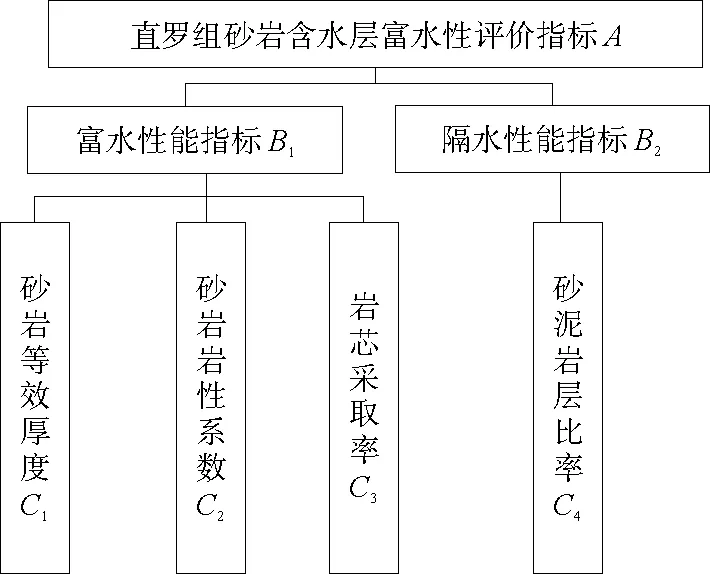
圖4 直羅組含水層富水性分析層次結構模型

2) 構造判別矩陣

依據(jù)Seaty等[15]提出的1～9標度法，根據(jù)各個評價指標對決策目標所起作用的大小進行兩兩比較，按重要程度評定等級，建立判別矩陣。例如：以研究對象A為目標，bi、bj(i，j=1，2，…，n)為第二層指標因素，bij代表了bi對bj的相對重要性，由此建立判別矩陣如式(10)、式(11)所示。

(10)

(11)

計算得4個評價指標M、S、P、Q的權重分別為0.221 7、0.351 8、0.093 1、0.333 4。

3) 確定各評價指標權重

將熵權系數(shù)法求得的權重w1、主成分分析法所得權重w2和層次分析法所得權重w3相結合確立綜合權重w，在保證結果客觀準確的前提下，結合實踐經(jīng)驗，對各權重進行約束求得組合權重(見表5)。

(12)

其中：w為綜合權重；n為影響因子個數(shù)。

表5 組合權重的計算

根據(jù)式(12)求得：

w=(0.288 1,0.287 6,0.087 3,0.337 0)。

(13)

4 富水性預測模型的建立及驗證

4.1 富水性預測模型的建立

依據(jù)式(12)計算的組合權重得出直羅組砂巖含水層富水性預測模型為：

D直羅=0.288 1M+0.287 6S-0.087 3P-0.337 0Q。

(14)

其中，D代表組合權重所計算的富水性指數(shù)，M、S、P、Q代表每個指標標準化值。指標P、Q與富水性呈負相關關系，因此P、Q指標前取負號。

根據(jù)式(14)得到研究區(qū)各個鉆孔的富水性指數(shù)，將富水性指數(shù)歸一化處理，再利用surfer軟件進行插值，統(tǒng)計得到富水性指數(shù)頻數(shù)直方圖(圖5)，確定分區(qū)閾值(0.2，0.5，0.6)。

同樣方法求得志丹群砂巖含水層富水性預測公式(15)，富水性指數(shù)頻數(shù)直方圖(圖6)。

D志丹=0.334 6M+0.254 6S-0.092 9P-0.317 9Q。

(15)

圖5 直羅組砂巖含水層富水性指數(shù)頻數(shù)直方圖

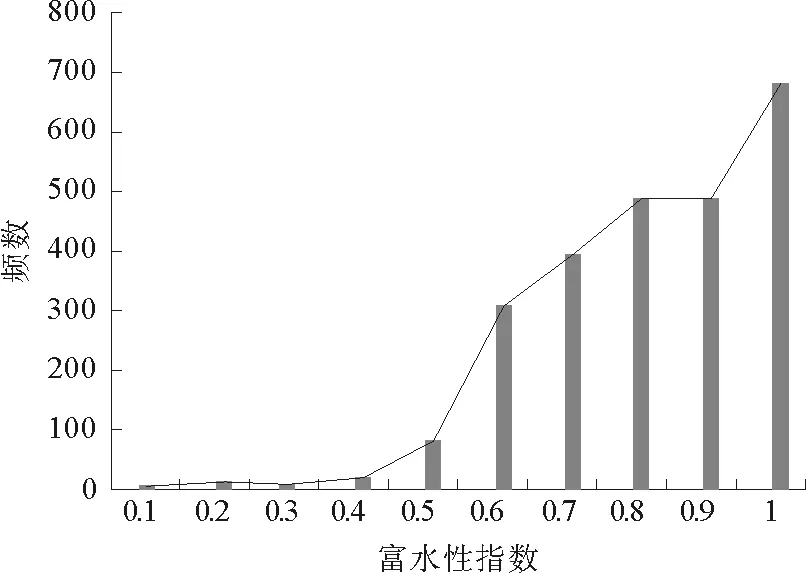
圖6 志丹群砂巖含水層富水性指數(shù)頻數(shù)直方圖

4.2 結果及驗證

鉆孔抽水層位于直羅組的鉆孔有K4-7、K4-9、X202、K8-4，單位涌水量q分別為：0.050 6、0.043 4、0.306 8、1.140 2 L/s·m。

根據(jù)《煤礦防治水細則》，含水層富水性依據(jù)鉆孔單位涌水量q值進行等級劃分，分為弱、中等、強和極強4個等級[16]。K4-7、K4-9鉆孔單位涌水量小于0.1 L/s·m，為富水性弱區(qū)；X202鉆孔單位涌水量區(qū)間為(0.1，1] L/s·m，為富水性中等區(qū)；K8-4鉆孔單位涌水量大于區(qū)間為(1，5] L/s·m，為富水性強區(qū)。因此，將富水性評價指數(shù)(0，0.2]定為弱富水性區(qū)，將(0.2,0.5]定為中等富水性區(qū)，(0.5，0.6]和(0.6,1]區(qū)間合并定為富水性強區(qū)，即研究區(qū)內不存在富水性極強等級。繪制22采區(qū)2煤頂板直羅組砂巖含水層富水性分區(qū)圖，如圖7所示。

抽水層位位于志丹群的檢3鉆孔、ZD-1鉆孔，單位涌水量分別是0.348、0.418 L/s·m。這兩個鉆孔均位于富水性中等區(qū)域，根據(jù)抽水試驗結果對富水性進行分區(qū)，繪制22采區(qū)志丹群砂巖含水層富水性分區(qū)圖如圖8所示。

富水性評價結果表明，直羅組砂巖含水層在22采區(qū)西北部大部分地段、東北部部分地段的富水性弱，東部和中部大部分地段富水性中等，有小范圍為富水性強區(qū)(圖7)。志丹群砂巖含水層大部分屬于富水性中等區(qū)域，西部、東南部富水性較強，東部和中部部分地段為弱富水性區(qū)(圖8)。

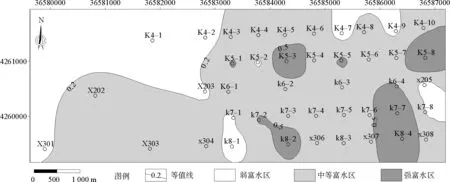
圖7 直羅組砂巖含水層富水性分區(qū)圖

圖8 志丹群砂巖含水層富水性分區(qū)圖

4.3 分區(qū)結果差異對比與分析

基于傳統(tǒng)單一主成分分析法得到的直羅組富水性分區(qū)圖如圖9所示，由圖可知，兩種方法所得結果總體相似，但由于賦值方法側重不同，在局部區(qū)域分區(qū)結果方面存在一定差異，如：①研究區(qū)西南部，EWM-PCA-AHP三種方法結合分區(qū)結果表現(xiàn)為較大面積的中等富水區(qū)，而單一主成分分析法表現(xiàn)為弱富水區(qū)；②K4-6鉆孔附近區(qū)域，EWM-PCA-AHP三種方法結合分區(qū)結果表現(xiàn)為中等富水區(qū)，而單一主成分分析法表現(xiàn)為弱富水區(qū)。以上差異反映了兩種方法在衡量富水性強弱上存在不同，主要因為，EWM-PCA-AHP三種方法綜合考量了各方法各指標在富水性上的全面表現(xiàn)，而主成分分析法一般只能提取解釋80%以上的成分，忽略了部分特殊因子，導致在相同級別下的富水性區(qū)間面積較三種方法結合得到的結果更大。

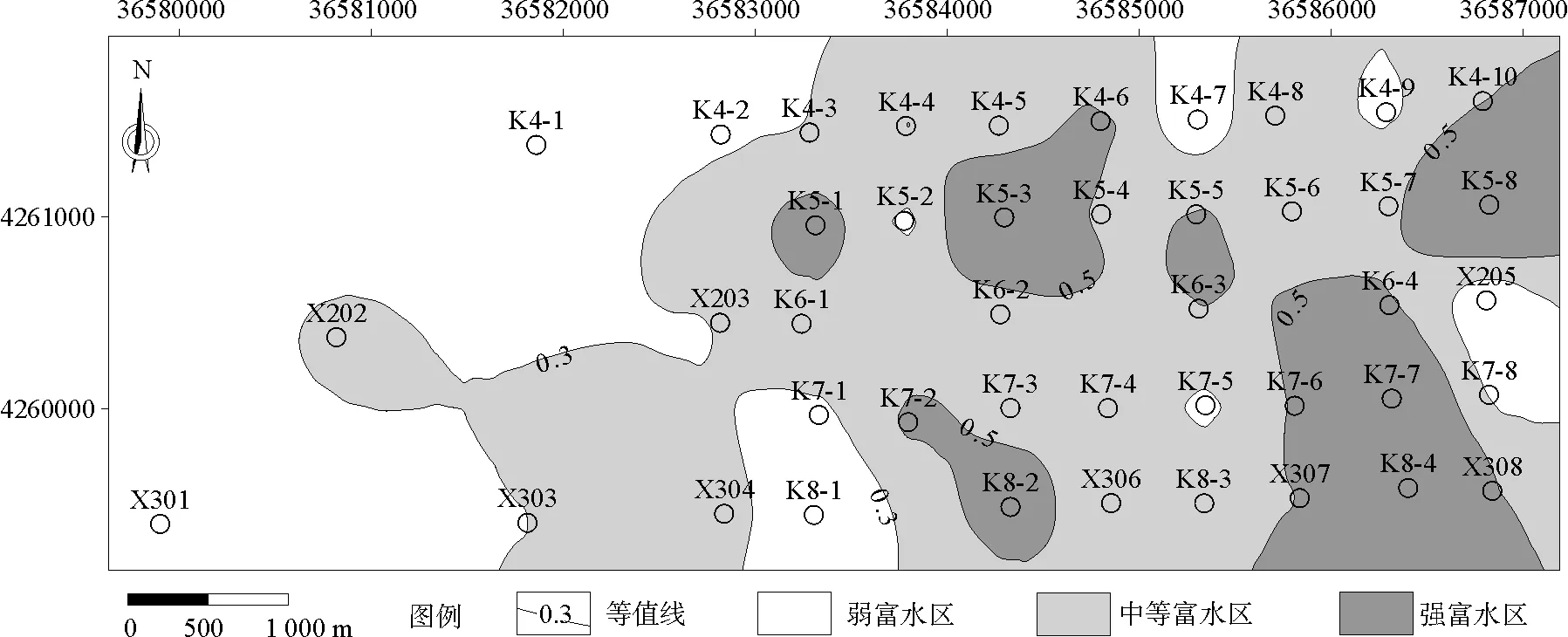
圖9 基于主成分分析法的直羅組砂巖含水層富水性分區(qū)圖

5 結論

1) 在構造簡單地區(qū)，沉積環(huán)境是控制該地區(qū)地層中含(隔)水層空間分布與含水層富水性的主要因素。研究區(qū)域構造活動微弱，砂巖含水層含水介質主要為孔隙，選取砂巖的等效厚度、砂巖巖性系數(shù)、巖芯采取率以及砂泥巖層比率4個因素作為判別指標構建模型。

2) 基于砂巖含水層的巖性及其結構特征，運用熵權系數(shù)法、主成分分析法和層次分析法確定的綜合權重建立頂板砂巖富水性評價模型，并作出預測及分區(qū)，三種方法優(yōu)勢互補，避免了單一方法的片面性，提高了評價結果的可靠度和準確性。

3) 評價結果表明，研究區(qū)直羅組和志丹群砂巖含水層富水性變化于弱-強范圍，不存在極強富水區(qū)，其中直羅組砂巖含水層富水性以弱-中等為主，志丹群砂巖含水層富水性以中等-強為主。經(jīng)與鉆孔抽水試驗獲得的單位涌水量資料進行對比，富水性分區(qū)結果合理，說明該預測方法是可行和有效的。