基于小批量K均值預分類的多波束反向散射強度角度影響改正

韓 冰，馮成凱，印 萍，梅 賽，張 凱，陽凡林,3

(1.山東科技大學 測繪科學與工程學院，山東 青島 266590；2.青島海洋地質研究所，山東 青島 266071；3.自然資源部海洋測繪重點實驗室，山東 青島 266590)

多波束聲吶(multi-beam echosounder，MBES)作為海洋測量的重要手段，具有高效、穩定、準確等突出優點，廣泛應用于海底地形地貌測量、海洋地質調查、海洋環境調查等諸多領域[1-2]。多波束聲吶系統以條帶測量方式實現海底全覆蓋測量，在獲得水下地形地貌的同時還可獲得高分辨率海底聲吶圖像，為測區大范圍海底底質分類、海底目標探測提供了可靠技術支撐。由于海洋環境以及聲吶系統本身的復雜性，聲信號在傳播過程中受到海水吸收、聲信號擴展、海底地形起伏、環境噪聲和海底混響等影響。隨著聲學理論及散射理論的日趨完善，對于上述影響因素基本都可去除或削弱[3]。受聲散射模型機理影響，不同入射角度下的回波強度不同，稱為角度響應(angular response，AR)[2,4-5]。由于波束的實際入射角直接影響AR曲線形狀，AR改正前需考慮換能器安裝偏差、聲線彎曲、地形起伏變化等因素的影響以建立嚴密的海底入射角計算模型[6-8]。

目前，國內外諸多學者已開展對AR模型及改進模型的研究。現有的AR模型建立方法主要有聲學模型法和數學統計法，聲學模型法主要是通過聲散射公式推導反向散射強度與入射角的關系，進而建立散射理論模型，目前主要有Lambert模型[9-10]、Jackson模型[11]、Hellequin綜合聲學模型[12]等；數學統計法通過統計反向散射強度隨不同入射角的變化規律而建立AR數學模型，主要有高斯擬合模型[13]、二次微分AR模型[3]等。前者雖考慮聲散射機理，但只是近似模型，不能夠準確描述不同儀器設備、復雜海洋環境下的角度響應，改正入射角效應時也引入了模型誤差；后者通過數學統計來描述角度響應曲線，但在底質變化復雜的區域，角度響應曲線會發生突變，AR改正時會引起聲吶圖像局部異常。

為此，通過研究上述問題的成因，提出一種基于海底點預分類的反向散射強度AR改正方法，以期提高多波束聲吶成圖質量。

1 多波束聲散射原理

多波束換能器能通過波束導向向海底發射并接收獲得一系列波束，得到不同強度的波束回波信號。如圖1所示，聲波到達海底后，只有在特定方向發生聲反射，剩余部分聲能量將在海底發生散射和折射，其中只有少部分反向散射能量被換能器接收(通常為-10～-40 dB)[14]。經過系統改正后，回波強度除與海底入射角相關外，還與聲波頻率、海底底質類型等因素相關[3]。海底粗糙度影響海底聲散射過程，當粗糙度大于波長時，海底回波強度與頻率無關；當海底粗糙度中有部分小于波長時，海底回波強度隨頻率增加，聲波頻率效應對海底回波強度的影響需預先去除[1]。通過對實測數據統計發現，泥質海底的固有反向散射強度為-19.7 dB，砂質海底為-20.2 dB，沙礫海底為-11.7 dB，巖石海底為-5.6 dB[1]，其中巖石、沙礫等為高阻抗平滑底質，對聲波有較強的散射性；細沙、泥質等為低阻抗粗糙底質會吸收較多的聲能量，表現為較弱的散射回波[14]。

對于小入射角，回波信號主要為反射回波，且包含較多噪聲干擾[15]，稱為小入射角區(D1區)；隨入射角的增加，回波信號主要來自海底底質的反向散射回波，稱為漫發射區(D2區)；D2區之外的大入射角區域，回波強度隨入射角表現為線性相關，稱為高入射角區(D3區)[16]。

圖1 海底聲散射示意圖

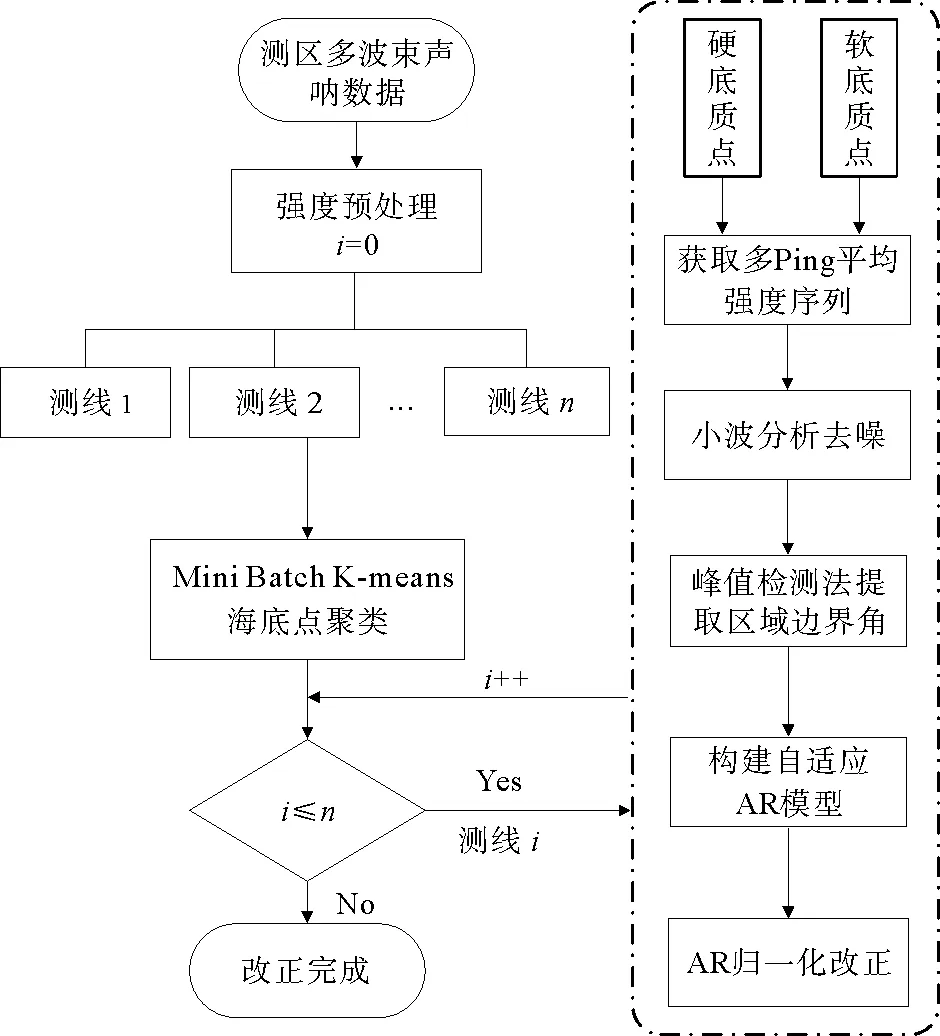
圖2 本文方法流程圖

2 基于預分類的多波束AR改正

準確獲取反向散射強度圖像是進行底質分類和聲吶圖像判讀的基礎。在進行AR改正時，發現聲吶圖像局部條紋和拼接異常通常發生在高阻抗平滑底質和低阻抗粗糙底質的交界處。這是由于高阻抗平滑底質和低阻抗粗糙底質反向散射強度相差在10 dB以上，在利用傳統方法進行統計和AR建模時會因為角度響應曲線突變造成模型誤差。因此，如何在AR改正前對高阻抗平滑底質和低阻抗粗糙底質進行區分成為關鍵問題。為方便描述，將高阻抗平滑底質稱為硬底質，低阻抗粗糙底質稱為軟底質。首先，利用小批量K均值(mini batch K-means)聚類算法[17]對強度預處理后的海底點預分類為硬底質點和軟底質點。在已知海底硬底質點和軟底質點分布的前提下，考慮局部海底底質變化且避免偶然誤差的影響，對連續多次聲脈沖(Ping)回波強度數據取均值獲取其局部平均角度響應曲線。然后，對角度響應曲線進行小波分析去噪、峰值探測區域邊界等步驟構建自適應AR改正模型。最后，去除反向散射回波信號的AR效應，通過地理編碼準確地獲取測區海底聲吶圖像。本文方法流程如圖2所示，其中i為當前所處理的測線，n為所處理測線總數。

2.1 Mini batch K-means海底點聚類

為保證測區條帶間聚類標準一致，應對所有測線海底點進行整體聚類。就淺水多波束系統而言，單條測線的海底點云數量可達100多萬，整個測區點云數量則更為龐大，對于計算效率和計算機性能也是極大的考驗。K-means算法計算復雜度低、聚類效果好，非常適于大型數據集的探索性聚類分析，但直接采用K-means算法對原始點云進行聚類時計算效率并不高。Sculley等[17-18]提出的mini batch K-means算法通過每次選取小批量數據進行K-means聚類，利用學習稀疏簇中心的方法，減小了計算耗時和存儲開銷。為避免角度因素對強度聚類的影響，聚類應在同角度間隔下進行，本mini batch K-means海底點聚類算法如下：

1) 初始化：海底點強度樣本按等角度間隔α劃分為子樣本Iu(u=1,2,3…)，聚類簇數g=2，最大迭代次數M，記每個類別的樣本數量為：N1,N2,…,Nk，樣本總數為N，mini batch個數b=1 000，中心計數v=0。

2) 從子樣本Iu中隨機選取g個樣本點作為初始的強度聚類中心點:{μ1,μ2,…,μj}。

3) 從子樣本中Iu中隨機選取b個海底點。

4) 計算樣本點bi到各聚類中心的距離

(1)

5) 利用梯度下降法，對每個樣本點bi(i=1,2,…,b)對應的最近聚類中心μj(j=1,2,…,g)據式(2)～(4)進行更新：

v[μj]=v[μj]+1，

(2)

(3)

μj=(1-η)μj+ηbi。

(4)

6) 重復3)～5)步，直至達到最大迭代次數，則子樣本Iu聚類結束。

7) 所有子樣本Iu完成聚類，輸出聚類結果。

2.2 反向散射強度AR改正

多波束反向散射強度同時受入射角和底質類型的影響。2.1節中算法可將海底點區分為硬底質點和軟底質點，但巖石和沙礫等雖同屬硬底質，其AR曲線也表現出細微差別，為更好地顧及海底局部底質變化，本研究分別針對硬底質點和軟底質點前后連續100 Ping作為滑動窗口，對同角度下反向散射強度取均值獲取平均AR曲線。

2.2.1 AR曲線小波去噪

平均AR曲線可以較好地表達反向散射強度隨入射角的變化趨勢，然而實際曲線中局部仍有較小的波動，特別表現在受反射影響較大的小入射角區(D1)[15]，為消除偶然誤差及粗差的影響，需要對曲線進行去噪平滑處理。

離散小波變換(digital signal processing，DWT)可通過小波基的尺度變換和位移對原始信號進行多尺度和多分辨率的探測，進而通過時頻域轉換去除信號中的高頻干擾。

(5)

其中，x(t)為待處理的平均強度序列，ψj,k表示母小波，j為縮放因子，k為平移參數。

Daubechies小波[19]為離散正交小波(簡寫為dbN，N是小波的階數)，具有時域、頻域局部處理能力，常用于信號去噪分析。dbN沒有明確的表達式，但轉換函數h的平方模是明確的。選取db4小波基對平均角度響應曲線進行n層分解得到信號低頻系數和高頻系數，然后通過逐層去除分解后的高頻系數進行平滑處理。如果分解層數過多，則曲線過于平滑，不利于邊界角的提取，如果分解層數較少，則會干擾邊界的提取。圖3為不同分解層數下的平均AR曲線小波去噪效果，通過對比分析發現，當n=3時曲線已經足夠平滑，n>3時會過平滑，則n=3即為最優分解層數。最后通過分解系數波形重構，可得到準確的AR曲線。

圖3 不同分解層數下的平均角度響應曲線小波去噪效果

2.2.2 AR曲線邊界提取

對去噪后的平均AR曲線可采用峰值探測法快速獲得分區邊界[20]。經驗數據表明D1～D2區的邊界角在10°～35°之間，D2～D3區的邊界角在40°～60°之間，兩邊界角位置對應的強度值均為局部極小值，因此可在上述兩角度區間內對平滑后的平均強度序列提取局部極小值點。極小值點處對應的入射角為：

θ=A(find(diff(sign(diff(BS)))<0)+1)。

(6)

其中：BS為平均強度序列，A為對應的角度序列，diff為差分運算，sign為符號函數，find指查找滿足條件的序列號。

由于隨機誤差及復雜底質的影響，在兩角度區間內可能存在多個局部極小值點，因此須將極小值點進行篩選。如圖4所示，Port表示左舷，Starboard表示右舷，在10°～35°區間，AR曲線在小入射角區呈大斜率變化，在漫反射區大致符合Lambert法則，通過計算兩相鄰局部極小值點的斜率k，其中k發生突變的點對應的角度θD1～D2即為D1～D2區邊界角；在40°～60°區間，對獲得的局部極小值進行排序，其中最小值對應的角度θD2～D3即為D2～D3區邊界角。為平穩過渡D1、D2區，還應在θD1～D2左右一定范圍內設立過渡區D1,2。

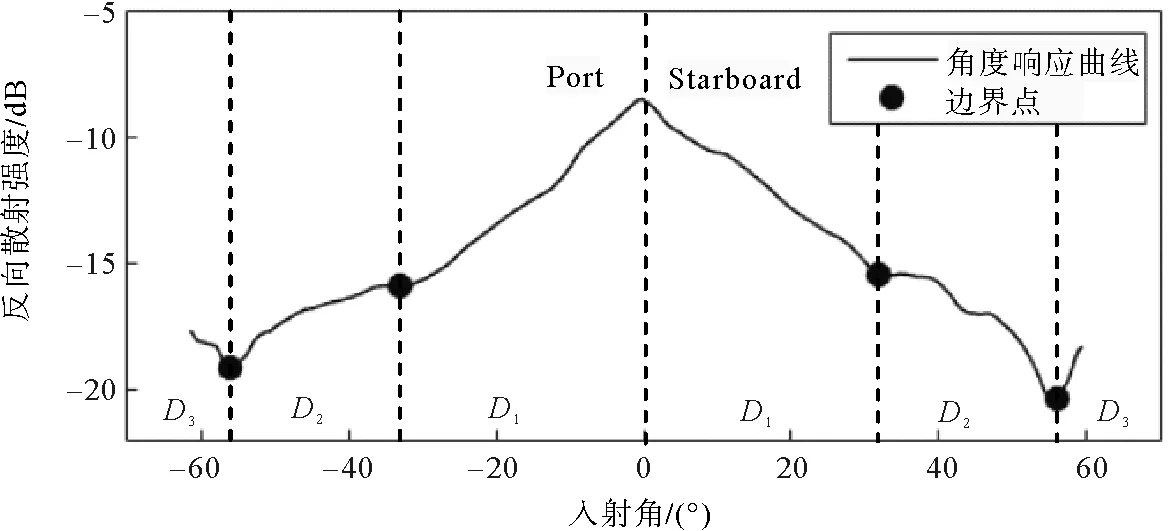
圖4 峰值探測法多波束角度響應曲線邊界角提取

2.2.3 AR自適應模型構建

從圖4可以看出，真實的AR曲線并不完全服從傳統Lambert法則模型，且在不同的區域表現為不同的曲線類型。為了克服Lambert法則模型存在的不足，針對三個主要分區及過渡區的特點，依據2.1節中提取的區域邊界，并綜合二次微分AR模型給出改進的自適應AR模型：

(7)

k=k2-[10lg(cos2θ2)-10lg(cos2θ1R)]/(θ2-θ1R) 。

(8)

式(7)～(8)中，θ為波束海底入射角；BSi(i=1,2,3)為Di區的起始強度值；θi為分區邊界角，θ1L和θ1R為過渡區邊界角；ki(i=1，2，3)為Di區的平均斜率，可由平均角度響應曲線離散點序列線性回歸求取；k為D2區的補償斜率，用于補償自適應AR模型與Lambert法則之間的的差值；fit函數為過渡區擬合函數，本研究選取三次多項式擬合函數；BSm為自適應AR模型值。

2.2.4 AR影響去除

對于中國農民而言，“糾紛寶塔理論”所刻畫的由下至上的糾紛解決層級結構并非是一個需要“攀爬”的實體[14]，而是一個可以靈活選擇而跳躍達至的扁平結構。鄉土正義系統是糾紛解決過程中以農民的法律資源選擇為主的法律秩序公共品集合體。就本文的分析所及，鄉土正義供給系統看似具有層級性，但在農民進行法律資源選擇的過程中，正義系統中的部件結構卻是扁平化的，農民既可以找村干部調解糾紛，也可以向派出所尋求幫助，也可以綜合利用鄉鎮政府的熟人關系網絡來促成糾紛的解決。

2.2.3節中給出自適應AR模型可以很好地表達不同入射角下反向散射強度的變化規律，因此要去除AR的影響，可針對單Ping的反向散射強度減去自適應AR模型值。為獲得底質的真實反向散射強度，應再加上左右舷波束在漫反射區(D2區)的平均回波強度[13]，海底點真實強度值由式(9)～(10)計算。

BSn=BS-BSm+BSmean，

(9)

BSmean=(BSport+BSstarbord)/2。

(10)

其中，BSn為AR改正后反向散射強度值，BS為AR改正前反向散射強度，BSm為AR模型值，BSmean為底質在漫反射區的平均回波強度，BSport與BSstarboard分別為左、右舷波束漫發射區平均強度。

圖5 海底預分類效果圖

3 實驗與分析

為驗證本文算法，選取2016年4月于浙江舟山某海域實測多波束數據進行分析，選取4條相鄰測線來說明。測量采用R2Sonic2024多波束測深系統，波束開角120°，聲吶頻率400 KHz，波束個數256個，測區位于長江入海口,水深20～30 m，海底底質較為復雜，原始數據已進行傳播損失、聲吶參數、聲照區面積等改正，經上述步驟改正后的回波強度主要受AR效應的影響。

3.1 實驗結果

3.1.1 預分類結果

將預處理后的海底點按照其強度屬性進行mini batch K-means聚類，4條測線上共計海底點487萬個，聚類簇數為2，為保證分類準確率，設置角度間隔α=1°，迭代次數為500次，聚類總耗時10.03 s。圖5為海底點預分類效果圖，其中圖5(a)為經過地理編碼的AR改正前海底聲吶圖像，圖5(b)為經噪點剔除及地理編碼的軟、硬底質分布圖，通過對兩圖分析可以發現，本文算法可以有效區分軟、硬海底底質，且分界明顯、自然，可見本mini batch K-means算法對于數據量龐大的海底點預分類具有可行性。

3.1.2 AR改正結果

從圖5(a)可以看出，角度響應對回波強度有較大影響，很難直接對AR改正前的聲吶圖像進行海底目標判別和底質分類。在預分類完成后，針對每條測線逐類進行AR改正。為便于比較，選取Lambert模型法、二次微分法與本文方法改正結果進行分析。對改正后的4條測線進行地理編碼，拼接后的測區海底聲吶圖如圖6所示。利用Lambert模型法改正(圖6(a))后，一定程度上去除了AR，但測線重疊區有明顯拼接痕跡，圖像整體較為模糊；二次微分法改正(圖6(b))后測線整體散射強度較為均衡，而從圖中仍可看到測線邊緣痕跡；本文方法改正(圖6(c))后，有效去除了AR，測區整體圖像清晰，測線過渡自然。

圖6 不同方法改正效果比對

3.2 討論與分析

最大信息系數(maximal information coefficient，MIC)[20]可以很好地檢測變量之間的非線性相關性，MIC值越接近0，說明反向散射強度與入射角的相關性越小，AR去除效果越好。通過與其他方法比較發現，本文方法MIC值最小，為0.123，說明本文方法AR去除效果最佳。為直觀表達，選取底質均一的相同區域20 Ping數據繪制強度散點圖，擬合其趨勢線，結果如圖8所示。

圖7 不同方法改正局部(圖6方框)效果比對

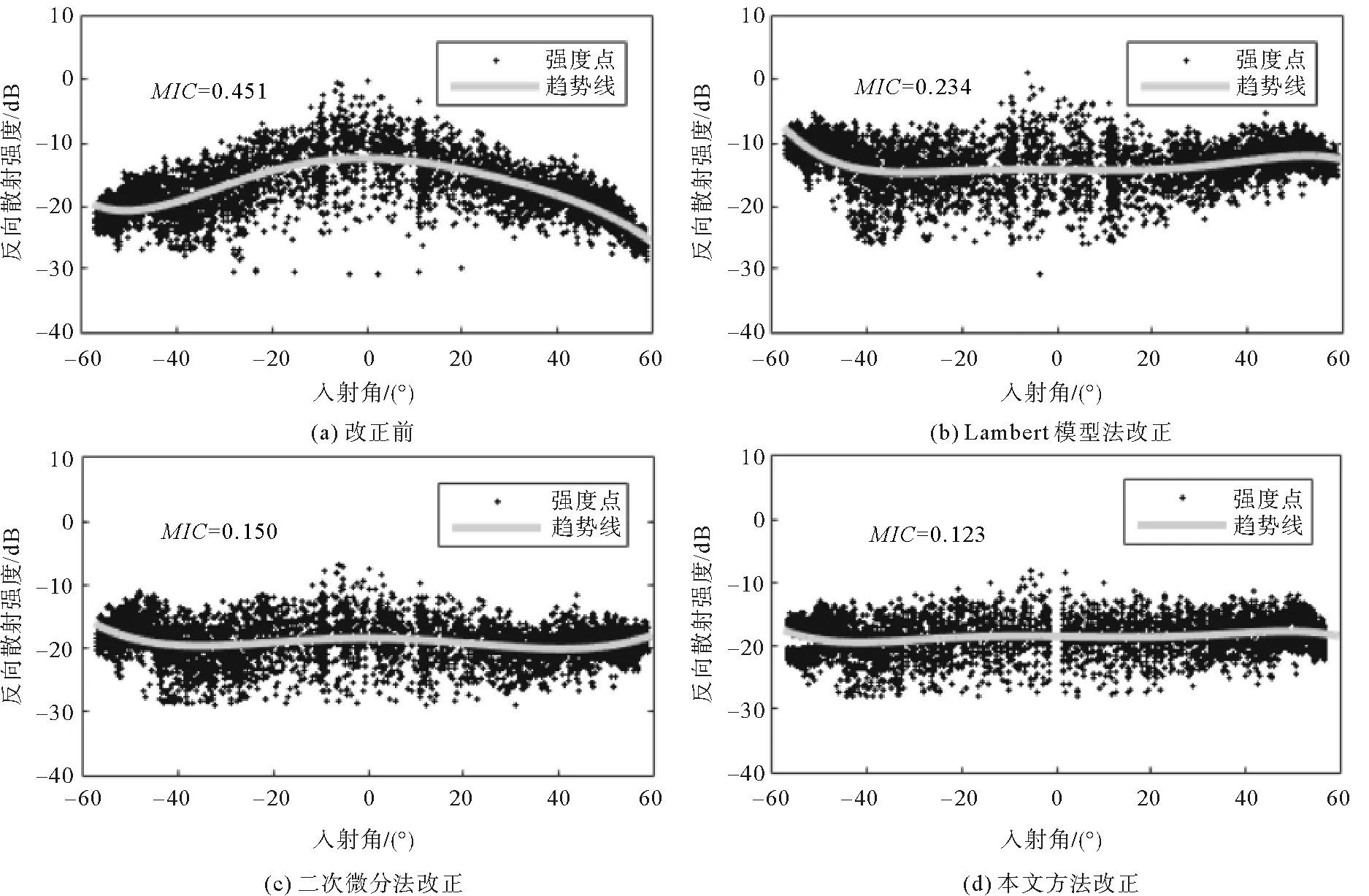
圖8 不同方法的AR去除效果

從圖8可以看出，三種方法均在一定程度上去除了角度響應的影響。由于Lambert模型邊界角的固定性，改正時反而引入了一定的誤差，其趨勢線仍然呈一定彎曲；相較于Lambert模型法，二次微分法對于AR的去除較好；本文方法改正后趨勢線基本呈直線，AR去除效果最好。

為進一步驗證評估該算法條帶拼接的一致性，選取4條測線的重疊區域進行分析。提取不同測線相同位置的回波強度差值，并統計其概率密度分布、均值和中誤差如圖9所示。

改正前測線重疊區回波強度值均值存在明顯的系統偏差，均值為-0.63 dB，標準差為5.48 dB；經Lambert模型法改正后系統偏差得到了修正，均值為-0.22 dB，但其標準差仍然較大，為3.32 dB；二次微分法改正后均值為0.73 dB，標準差有進一步改善，為1.83 dB；本文方法改正后重疊區強度差值概率分布峰值出現在0附近，均值為0.22 dB，基本符合正態分布，標準差為1.46 dB，較其他方法最小，進一步證明了本文方法的有效性。

圖9 測線重疊區強度差值概率密度分布

4 結論

基于聲散射理論研究并分析現有多波束AR改正模型的不足，提出了基于預分類的反向散射強度AR改正方法。通過對回波強度固有屬性差別較大的硬底質和軟底質進行預分類，保證了復雜海底底質環境下多波束AR曲線的準確提取，同時提高了測線間回波強度水平的一致性；利用小波函數進行角度響應曲線去噪，削弱了偶然誤差和粗差對角度響應曲線的影響；峰值探測法提取邊界角以及自適應AR模型的構建，實現回波強度AR效應的去除。

選取浙江舟山海域實測4條相鄰測線進行分析，并采用Lambert模型法、二次微分法與本文方法分別進行了反向散射強度角度響應去除。對比發現，本文方法處理后有效去除了多波束回波強度AR效應，角度因素與反向散射強度的相關性最小(MIC=0.123)，條帶重疊區反向散射強度標準差為1.46 dB，較其他方法小。從海底聲吶成像質量來看，本文方法處理后海底聲吶圖像清晰，不同底質分界明顯，有效解決了復雜底質環境下聲吶圖像局部條紋和整體明暗不一的問題，為后續底質分類等工作奠定了基礎。