通過連續多次課堂實驗開展博弈論教學

金誠杰 王昊 陳峻

摘要：通過課堂實驗進行博弈論教學，能夠有效促進學生對知識的理解。但在以往的實踐中，此類實驗通常只進行一次，效果不夠顯著。因此嘗試在連續幾周的課堂上開展博弈論實驗，并在每次實驗之間講解前一次實驗結果，對學生進行集體訓練。連續實驗結果表明，第一次實驗不可能達到納什均衡點，但在三周實驗之后，學生的集體選擇會逐漸接近均衡點，并且如果繼續重復下去，最終可以達到目標。這一過程有效地強化了學生對博弈論原理的認識。同時通過博弈論知識的學習，交通專業的學生也進一步加深了對交通分配中Wardrop第一和第二原理本質的理解。

關鍵詞：博弈論;課堂實驗;納什均衡;Wardrop原理

中圖分類號：G642.0? ? ?文獻標志碼：A? ? ?文章編號：1674-9324（2020）15-0378-04

一、引言

博弈論是研究理性人互動的理論。1928年，馮-諾依曼證明了博弈論的基本原理，宣告了博弈論的誕生。1944年，他和摩根斯坦合著的《博弈論與經濟行為》將二人博弈的情況推廣到多人博弈結構，并且將博弈論系統應用于經濟領域，奠定了這一學科的理論體系。在1950年，納什用不動點定理證明了均衡點的存在，為博弈論的一般化奠定了基礎。到今天，博弈論已經成為社會科學的通用方法論，對于理解各種社會現象具有非常重要的價值[1]。

為此，我國高校中很多專業都開展了博弈論知識的教學。由于博弈論的數學模型非常復雜，公式和符號抽象，學生通常不易理解，因此近年來很多學者開始在傳統課堂講授的基礎上，引入博弈論實驗的手段[2-6]。這種互動的教學模式更加有趣，有利于學生理解博弈的基本思想，也有助于活躍課堂氣氛和提高教學效率，是值得廣泛推廣的。但在以往的博弈論課堂實驗中[2-6]，基本上都只進行了一次實驗，內容過于簡單。有些學者在期末考試中引入了實驗內容[7]，它的效果也等同于單次實驗。事實上在一學期的連續多周課程里，完全有條件開展連續多次的重復課堂實驗，從而更深入地揭示博弈論原理，進一步強化學習效果。因此我們針對這一點展開了嘗試，取得了較好的效果，具體過程將在下文詳述。

二、第1輪實驗：初嘗試

我們設計的實驗內容如下：

在0—100之間選取一個數字，當所有學生的數字收上來之后，計算所有數字的平均數。選取數字最接近大家平均數2/3的學生是贏家，可以得到10元錢獎勵。如果有多個贏家，則每人都有10元錢獎勵。你將如何選擇這個數字？

實驗說明：

1.共有42名實驗參與者，均為東南大學交通學院一年級研究生，大部分學生專業為交通運輸規劃與管理，少數為道路、載運、ITS等專業，均無相關實驗經驗，也從未學習過博弈論知識。

2.實驗時間為15分鐘，在實驗過程中不允許和別人交談，也不允許上網查找資料，完全獨立完成。

3.參與者在白紙上寫上自己的姓名，學號，選擇的數字和理由。

這一實驗內容和文獻[6][7]描述的實驗基本一致，主要區別在于文獻[7]在期末考試中進行，將實驗內容設定為試題，而文獻[6]中要求為“數字最接近大家平均數1/2的學生是贏家”。在這次實驗過程中，學生非常投入，很多人在時間結束時仍然在反復思考和推算。實驗結束后，學生們對這個實驗表達出了強烈的興趣，例如下課時有學生表示希望能當場統計，當場出結果。

課后我們將42名學生的結果進行統計分析，按照每10個數為1個區間的方式進行劃分，結果如表1所示。由于沒有學生填寫80以上的數字，所以表格中的最大區間為（71，80]。在42個數字中，最小值為0，最大值為75，平均值為28.53，它的2/3為19.02。由于無人選擇19，所以最終贏家為2名選擇20的學生。

這一實驗存在著納什均衡點0或者1，具體的分析和推導過程可參見文獻[6]，本文不再贅述。此處主要討論實驗中發現的一些現象：

1.67以上的選擇肯定是非理性的，因為即便平均值為100，它的2/3也只有66.7。本次實驗中仍然有一名學生填寫了75，并且說理由是“我喜歡”，可以看到即便對于一年級的工科研究生而言，仍然有少數人不具備基本的理性思維能力。

2.有的學生雖然給出了理論上可能的數值，但理由很不充分，事實上他們并未進行合理的分析。例如一名學生填寫了61，理由是“我覺得大部分人會往黃金分割點靠近”。還有學生填寫了50或40，理由是“我猜的”。

3.一些學生努力地進行了推理演繹，并且接近了最終的答案。例如在42人中，有多達10名學生選擇了22，其中有代表性的理由是：

“如果沒有假設條件，平均分布的結果應該是50，則50*2/3=33。可能大家都會想到這一角度，所以答案平均值會接近于33，則2/3應該為33*2/3=22”。

4.也有學生在22的基礎上進一步演繹，繼續乘以2/3，并得到了14或者15的結果。但即便是考慮到了“無限循環”的情況，他們也并未選擇更小的數字（本次實驗中無人選擇1—10的數字）。

5.總共有2名學生選擇了0，他們分析出了納什均衡點，意識到在“無限循環”后，確實結果會趨向于0。但在這次實驗中，寫0事實上是一種非理性行為，因為如果大多數人未考慮到這一步的話，平均值必然遠大于0，寫0的人根本不可能成為最后的贏家。

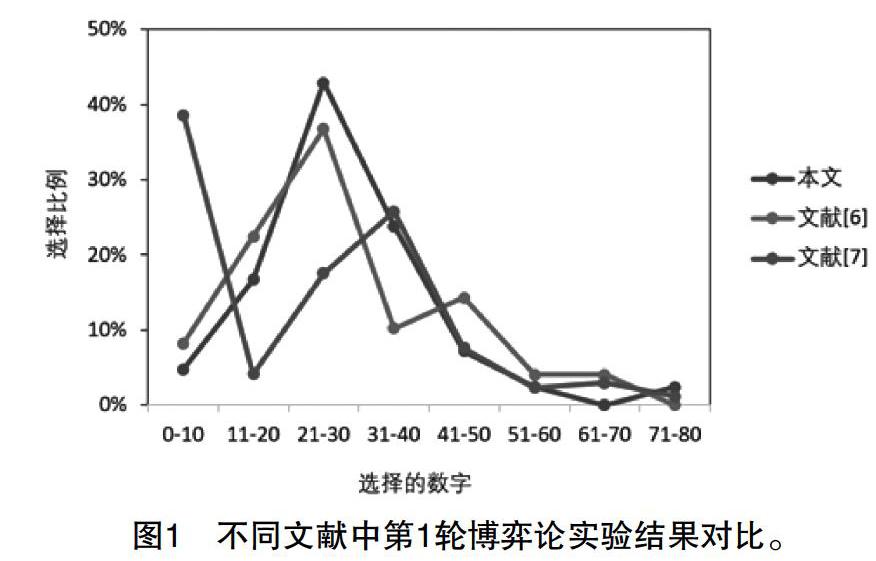
此處還可以將本文的實驗結果與前人的實驗結果進行對比。我們采集了文獻[6]和[7]的統計數據，并呈現在圖1中作比較。可以看到當選擇的數字較大（N>30）時，3次實驗的結果非常接近，尤其是N>50時幾乎完全一樣。在數字較小時，本文結果和文獻[6]的結果仍然基本一致，但文獻[7]呈現出不同的狀態，明顯有較多學生選擇了0-10這一區間，即更為接近納什均衡點。另外從平均數而言，本文實驗的結果為19.0，也明顯大于文獻[7]中的平均數14.6。

通過分析學生背景，可以發現文獻[7]中的實驗參與者是選修課邏輯與科學方法基礎的學生，并且這一實驗是期末考試中的一道題。此門課程的教師曾經以講座的形式給他們講授過博弈論知識，所以他們經歷過一定的訓練，具備了更強的思維能力。而本文和文獻[6]的實驗參與者，在實驗前并未系統學習過博弈論，相對而言思維能力較弱，所以能考慮到納什均衡點的學生明顯較少。

三、第2輪實驗：訓練的效果

如前文所述，第1輪實驗過程事實上與文獻[6][7]幾乎一樣，并無多少創新之處。為了進一步加強學生對博弈論的理解，教師決定接下來進行更多更深入的實驗。

首先，在第2周的課堂上，教師對第1輪實驗的結果進行了介紹，包括公布了選擇不同區間的人數比例和最終平均值，并且向學生具體分析了實驗原理，指出選擇0是納什均衡點，但事實上在第1次實驗中選0不可能成為贏家等等。此時學生開始對博弈論有了基本的認識，初步具備了策略性思維的能力，并且學習興趣得到了進一步加強。

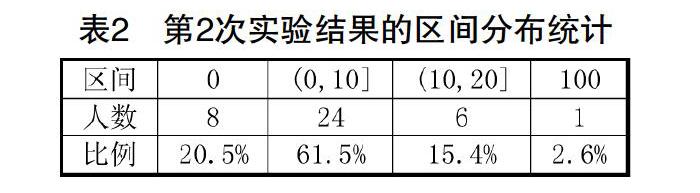
然后，教師立即在課堂上開展了第2輪實驗，并且實驗內容、過程和第1輪完全一樣。但因為參加實驗的學生經過了一次訓練和學習，效果必然會有所不同。這次實驗的結果如圖2所示■，可以看到在了解了原理之后，大家的選擇普遍更接近于0，平均值比第1次實驗小了很多，并且有更多的學生（8名）直接選擇了納什均衡點。其中有2名學生在選擇理由中直接指出，所有人選擇0會導致系統最優，即“這樣每個人都是贏家，每個人都可以獲得10元錢獎勵”。但與此同時，仍然有很多人考慮到“參與者不可能絕對理性，不可能大家都選0”，所以大多數學生（24名）選擇了1—10之間的數字，并且有少數人（6名）選擇了11—20之間的數字。這種對他人的普遍懷疑導致第2輪實驗仍然沒有出現系統最優的結果，平均值最終為7.76，2/3結果為5.17，最終贏家為2名選擇5的學生。

值得一提的是，這次實驗中有一名學生選擇了數字100，并且在理由中寫道：“反正我拿到錢的概率很小（或者說沒有概率），就來做個不理性的破壞者吧。”由于他在平時是一個做事認真細心、守規矩、學習成績比較好的學生，做出這樣的行為可以說是令人意外的。但其實在生活中，我們也經常能觀察到類似于“損人不利己”的非理性行為;一個人在分析過形勢之后，感覺自己完全沒有勝算，于是選擇和對手“同歸于盡”，道理上也算是說得通。這一情形充分體現出博弈論的一些基本假設、例如假設“參與者是絕對理性的”往往與事實不符，這一點和前人研究結論[1，7]一致。可以說我們的實驗結果也是復雜人性的一次鮮活的體現。

四、第3輪實驗：接近納什均衡點

在第3周的課堂上，教師首先對第2周的實驗結果進行了介紹，公布了選擇不同區間的人數比例和最終平均值，并對大家的選擇做了進一步分析。學生們對實驗結果同樣非常感興趣，并且針對這輪實驗中有人故意選擇100的意外情況展開了熱烈的討論。

然后，教師在課堂上開展了第3輪實驗，并且實驗內容、過程和第1第2輪完全一樣。此時學生們已經意識到，這個實驗的最佳策略是所有人合作，全部選擇0，這樣所有人都是贏家，所有人都可以獲得10塊錢獎勵。但同時，由于“前車之鑒”的存在，大家也會擔心是否又有人搞破壞。在這兩項因素的綜合作用下，這次實驗的結果比上一次更加接近于納什均衡點，但并沒有達到。具體結果如表3所示，這次的平均值為3.67，2/3結果為1.97，最終贏家為4名選擇2的學生。

在第3次實驗中，雖然有幾名學生在寫理由時談到可能會有人搞破壞，甚至有學生預測說“這輪一定有更多的人搗亂，我猜應該有5—6個人”，但最后并沒有出現這種情形：這次的最大值只有16，并且選擇（11，20]的人只有2名。事實上正如另一名學生所預測的那樣，“本次會有更多的人寫得更小，搞破壞的人在一次之后會覺得無聊，不會增加多少”。

總的來說，通過這次實驗我們可以觀察到，系統在逐漸向納什均衡點靠近，但這個靠近速度是很慢的。例如選擇0的學生數量只從8增加到了10，并且有4名上一輪選擇0的學生基于對整體的判斷，這次反而選擇了略大一些的數字。另外，已經有很多學生逐漸意識到了多輪重復實驗的意義所在，例如有學生在理由中分析到“想問的是，到底要經歷多少次實驗才會實現共贏呢”。

五、未進行的下一輪實驗：最后的討論

在第4周的課堂上，同樣地，教師首先對第3周的實驗結果進行了介紹，公布了選擇不同區間的人數比例和最終平均值，并對大家的選擇做了進一步分析。雖然學生仍然對實驗本身有興趣，但對于是否還要繼續重復相同實驗，已經有些爭議。事實上在第3次實驗的結果中，已經有不止一名學生寫到“對實驗失去興趣”或者“無法分析”。

顯然，當學生對實驗內容失去興趣時，這個實驗就無法再促進教學了。因此這次課上，教師先請學生們針對“是否要繼續做第4輪實驗”舉手表決，結果發現大約80%的學生都認為沒必要再做，并且大家普遍相信，假如繼續做下去最終必然會達到納什均衡點，所有人都會寫0。唯一的懸念是還需要幾輪才能達到，但這一輪數似乎并不重要。到此時，博弈論實驗可以說圓滿結束了：通過連續4周的學習和討論，學生親身體驗了決策過程，在與集體的互動中深刻領會了博弈論的含義與樂趣，實現了較好的教學效果。

六、與交通工程知識的聯系：以Wardrop原理為例

前文所述的幾次博弈論實驗，雖然非常有意義，但和交通工程領域并無直接聯系。對于交通運輸規劃與管理的學生而言，還需要學以致用，能夠將博弈論知識用于自己的專業領域。事實上很多交通問題都屬于博弈論的范疇，只是由于交通參與者通常數量較多，往往難以使用博弈論直接求解。但使用博弈論的思維方式，仍然可以解釋一些交通現象，加深學生的理解和認識。

此處我們以交通分配中的Wardrop原理為例，進行簡單的詮釋。Wardrop第一原理認為，網絡上的交通分布結果，會使得所有使用的路線都比沒有使用的路線費用小。Wardrop第二原理認為，車輛在網絡上的分布，使得網絡上所有車輛的總出行時間最小。如果交通分配模型滿足Wardrop第一、第二原理，則該模型為平衡模型，并且滿足第一原理的模型稱為使用者優化平衡模型（User—Optimized Equilibrium），滿足第二原理的模型稱為系統優化平衡模型（System—Optimized Equilibrium）。如果模型不滿足這兩條原理，而是采用了模擬方法，則被稱為非平衡模型。

交通工程教科書上[8]會指出，非平衡模型在實際工程中得到了廣泛應用，效果良好，但卻沒有具體說明為何平衡模型使用效果不佳，為何Wardrop原理經常失效，導致學生往往并不明白其中原因。但如果結合博弈論和納什均衡，則可以給出解釋：

Wardrop第一原理基于用戶的理性假設，認為用戶總是盡可能地最小化自己的通行時間，所有的用戶都如此選擇的結果形成了用戶均衡。Wardrop第二原理假設用戶是合作的，最終使得系統總的通行時間最少。然而從納什均衡的結果來看，Wardrop第一和第二原理之間根本不存在關聯性，并且很多時候恰好相反：當所有用戶試圖滿足Wardrop第一原理時，經常導致Wardrop第二原理得不到滿足，系統的總時間會變大。這在著名的“囚徒困境”中有充分的體現：每個囚徒都會選擇坦白，從而導致所有人都坐牢更長時間。而在我們的課堂實驗中，會有很多學生在認真思考后仍然選擇較大的數字，從而提升整體平均值，延緩系統達到均衡點的速度。更特殊的是，在少數時候，用戶甚至不滿足Wardrop第一原理：例如在我們的課堂實驗中有學生故意選擇100，干擾大家的結果。另外即便有教師指導，在大家經過3輪的集體學習和訓練之后，仍然只是接近、而未達到系統均衡點，換言之系統的收斂速度沒有之前想象中快。由此可以看出，要想在現實中讓交通分配結果同時滿足第一和第二原理，根本是不可能的，這也就是非平衡模型更實用的原因。

當我們在課堂教學中分析了這一點之后，學生普遍感覺到了學習博弈論對解決交通問題的幫助，同時也對交通分配方法和Wardrop原理有了更深刻的認識。

七、結論

為了提升教學效果，克服單次實驗的缺陷，本文通過開展連續多次的課堂實驗進行博弈論教學。結果表明，第一次博弈論實驗不可能達到納什均衡點，但在三周實驗之后，學生的集體選擇會逐漸接近均衡點，并且如果繼續重復下去，最終可以達到。通過這一系列的實驗，學生充分地了解了博弈論的基本原理，親身體會了決策過程，學習興趣得到了充分的激發。另外通過博弈論知識的學習，交通專業的學生也加深了對交通分配中Wardrop第一和第二原理本質的理解。在今后的教學實踐中，我們計劃針對更多的學生開展類似的實驗，比較各次實驗結果之間的相同點和不同點，進一步促進學生對博弈論和相關知識的理解和掌握。

注釋：

（1）由于少數學生請假和曠課的緣故，第2次實驗只有39名學生參加，第3次實驗有40名學生參加，但這種差異對實驗結果的影響基本可以忽略不計.

（2）為保護隱私，選擇100的學生姓名并未公布，大家只是知道班里有一個人做出了這樣的行為.

參考文獻：

[1]劉曉麗.博弈實驗對博弈論的方法論意義[J].學術探索，2013，（3）：24-28.

[2]李軍軍，黃茂興.課堂實驗在理論經濟學教學中的應用與創新[J].福建師范大學學報：自然科學版，2011，27（3）：110-113.

[3]李太龍.博弈論公選課的教學內容與方法探析[J].教育探索，2012，（1）：42-44.

[4]喬磊.實驗教學在經濟學課堂教學中的應用[J].教育教學論壇，2012，（7）：218-219.

[5]李攀藝，周伍陽.經管類本科專業博弈論課程教學探悉[J].科教導刊-電子版（中旬（，2014，（7）：59.

[6]王新輝，黃鶯，彭怡.博弈論策略性思維的課堂教學實現[J].西南民族大學學報：自然科學版，2015，41（3）：345-34.

[7]劉曉麗.從博弈實驗看博弈論作為社會科學方法論的局限性[J].東南大學學報：哲學社會科學版，2012，14（4）：20-22.

[8]王煒，過秀成，等.交通工程學[M].南京：東南大學出版社，2003.