電能質量異常數據在線檢測方法
劉 杰,房 俊,雷峰津
1.北方工業大學 計算機學院,北京100144
2.大規模流數據集成與分析技術北京市重點實驗室,北京100144
1 引言
異常數據(Outlier)的定義由Hawkins 于1980 年給出,它指的是在數據集中偏離絕大部分數據的數據,由于其偏離了絕大多數數據以至于人們常常懷疑這些數據是由與大多數數據完全不同的機制產生的[1]。
電能質量異常數據檢測識別作為國家電網“電網諧波監測分析模塊”的重要研究內容,其在電網安全隱患發現,運維檢修輔助決策等方面起著至關重要的作用。從長期(如季、年)來看,電網系統是一個不斷變化的系統;從短期(如天、月)來看,它是一個相對穩定的系統,同一個監測點的同一指標數據都以天為周期呈現規律性的變化,具有一定的時序特性,如圖1 所示(數據來源:由國家電網“電網諧波監測分析模塊”采集的2018年6月1日至4日電壓偏差數據)。

圖1 電壓偏差日數據變化對比
目前數據異常識別方法主要有經驗閾值法、基于數據挖掘的方法和基于數理統計的方法[2-3]。經驗閾值的確定具有一定的主觀性,一旦閾值確定就不輕易更改;基于數據挖掘方法通常是根據數據的特點進行建模,然后進行數據的異常檢測;基于數理統計的方法要求數據具備一定的統計特性,服從一定的分布[2-5]。由于電能質量數據的特殊性和以上方法自身的局限性,無論是經驗閾值、數據挖掘還是數理統計方法都無法完整、有效地識別出電能質量數據中的異常數據。
控制圖(如圖2 所示)是一種將顯著性統計原理應用于控制生產過程的圖形方法[6-7]。它利用從可重復過程所得到的數據,建立由中心線(CL)、上控制線(UCL)和下控制線(LCL)組成的一個帶狀區域來識別過程的穩定性和控制過程的調整。控制圖在建立上下控制線的過程中會剔除訓練數據中的異常數據,使控制線處于穩定狀態。在在線數據異常檢測過程中,過程控制圖可以在O(1)時間復雜度內滾動更新控制線。統計控制圖方法成熟,在生產程序控制中得到廣泛運用并取得良好效果,其經驗參數具有很好的實用價值,并形成了相關國標[7-8]。
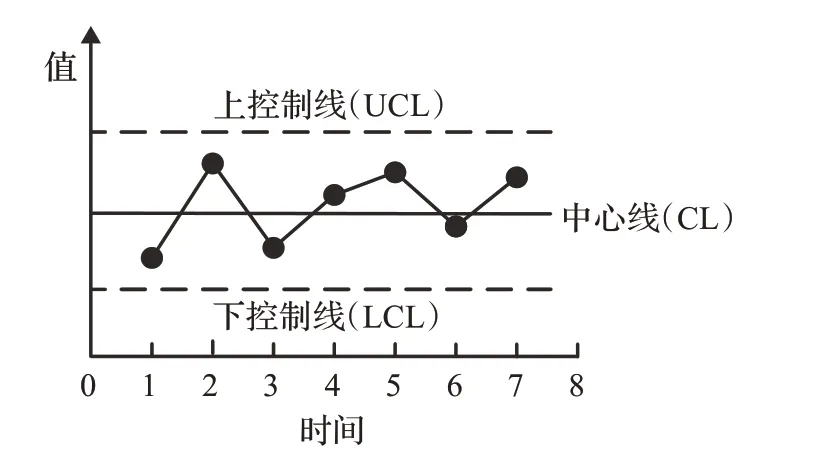
圖2 傳統控制示意圖
控制圖在生產過程控制和產品質量檢測中都有廣泛的運用,在這些運用領域,數據大多均值恒定,樣本總體服從正態分布。但是,電能質量數據與工業生產產生的數據存在較大差別:(1)電能質量數據呈現周期性變化的特點;(2)短時間內的數據波動范圍較大(如圖1 所示)。因此,傳統控制圖在對具備上述特征的數據的異常檢測方面適應性較差。本文根據電能質量數據的特點,結合控制圖和時間序列數據預測,對控制圖進行了改進,提出了基于控制圖的動態閾值電能質量異常數據在線檢測方法。
本文的主要創新點有:
(1)改進控制圖中控制線的計算方式,將控制圖控制線化直為曲,以適應數據的變化趨勢。
(2)將控制圖和時間序列預測相結合,實現控制圖控制線的動態調整,實現電能質量異常數據的在線檢測。
2 相關工作
從Hawkins 提出異常數據的概念開始,很多專家和學者分別針對各自面對的研究問題提出了不同的異常數據的檢測算法和檢測思路,其中也不乏針對電力行業數據的異常檢測研究,但是這些方法都無法完整、有效地檢測出電能質量數據中的異常數據。根據待檢測數據的有序性可將這些檢測辦法分為無序數據集的異常檢測和有序數據集的異常檢測兩類。
無序數據集的異常檢測方法大致可分為基于數理統計的異常檢測方法和基于數據挖掘的異常檢測方法。基于數理統計的異常檢測方法以統計學的統計量作為判斷異常值的準則,其基本思路是假定數據服從某種分布,然后建立概率模型,并將低概率區的數據判定為異常值。相關文獻有[4-5,9-11]。文獻[4]針對總體樣本方法確定的異常閾值受樣本隨機不確定性影響較大以及總體樣本方法對正常數據波動正常數據波動檢測失效問題,提出了一種基于云模型檢測諧波電流異常數據的方法;文獻[5]針對諧波電流監測數據經常偏離正態分布,利用正態分布確定的異常閾值不適用問題,采用三參數威布爾分布模型確定異常數據閾值;文獻[9]通過對供電端和用戶端的數據計算用戶用電欺詐系數,實現異常檢測;文獻[10]通過計算數據協方差矩陣中元素的變化實現異常數據的檢測;文獻[11]利用中位數原理估計方差殘差序列的期望和方差實現了數據的異常檢測;文獻[12]提出了一種動態閾值的變壓器異常狀態檢測算法,通過計算不同電壓等級、裝機容量下變壓器運行參數閾值,并計算不同狀態發生的概率來實現異常檢測。基于數據挖掘的異常值檢測方法較多,但是基本可以歸為分類和聚類兩類,基于分類的異常檢測需要大量的異常數據樣本;基于聚類的異常檢測結果受聚類結果的影響較大,如果聚類簇結果較差,異常檢測結果也較差;異常點對聚類個數敏感,不同的聚類簇個數可能會導致識別出差異較大的異常點。相關參考文獻有[13-14]。文獻[13]針對快速密度峰值聚類算法用于異常值檢測時未考慮數據的局部特點以及局部密度依賴于截斷距離選取的不足,提出了基于KNN 的快速密度峰值異常檢測算法;文獻[14]提出了一種基于神經網絡的數據建模方法識別火電廠中鍋爐的異常行為,但其實質還是對數據進行分類。
有序數據集的異常檢測方法主要是時間序列檢測算法。基本思想是對時間序列進行預測,然后通過估計值與測量值的差值來確定異常值。相關文獻有[15-17]。文獻[15]采用基于高階統計量的時間序列挖掘算法檢測異常數據,但閾值的確定受滑動窗口大小的影響。文獻[16]提出了一種基于時間序列提取和維諾圖的異常數據檢測方法,但是該方法適用于高維電能質量數據的異常檢測,并且方法中的重要點分段時間序列提取算法中參數k 的選擇對結果影響較大;文獻[17]提出了一種基于數據曲線斜率變化率進行異常檢測的辦法,其本質是突變檢測。
控制圖在電力行業的研究相對較少,文獻[18]提出了基于控制圖的電能質量數據動態限值分析方法,是控制圖在電能質量數據分析中的典型應用,但是其研究的時間窗口較大(如:月、季、年),通過該方法得到的限值仍然無法有效識別出更小時間窗口內(如:天)的異常值;文獻[19]給出了一種根據數據變化周期動態調整異常值閾值的方法(本文簡稱周期模型法),但是該方法主要是從整體上判定某一天狀態是否可控,而非檢測某一天的所有數據是否異常。
3 異常數據在線檢測方法
在使用控制圖進行異常數據檢測前,首先需要利用歷史數據對控制圖進行訓練使其達到初始穩態。在利用具備周期性變化規律、數據波動范圍大的特點的電能質量數據進行控制圖訓練時,由于數據波動較大,大量數據會被整組剔除以至于幾乎無法達到初始穩態,因此具備上述特點的原始電能質量數據不能用于計算控制圖的控制線,傳統控制圖對此類數據的異常識別適應性較差。
雖然傳統控制圖在進行具備周期性變化規律且波動范圍較大的電能質量數據異常檢測適應性差,但是,結合數據的周期性變化規律,可以將控制圖的中心線化直為曲,用數據的變化趨勢線替代控制圖的中心線,然后計算出控制圖的上下控制線,通過判斷數據是否處于上線控制線之間而判斷數據是否異常,改進控制圖示意圖如圖3所示。
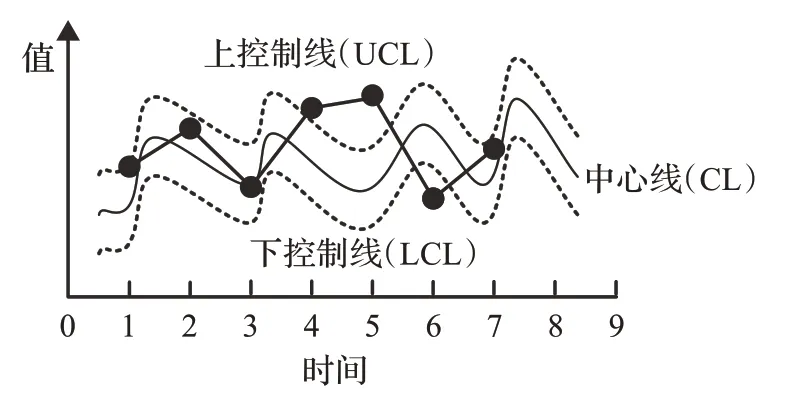
圖3 改進控制圖示意圖
利用如圖3 所示的改進控制圖對電能質量異常數據進行在線檢測可分為兩個階段:第一階段為數據預處理及控制圖初始穩態訓練;第二階段利用穩態控制圖對在線數據進行異常檢測。整個電能質量異常數據在線檢測任務可分為以下四個步驟:
(1)對電能質量歷史數據進行計算,獲得電能質量數據變化趨勢數據(即改進控制圖的中心線)。
(2)利用趨勢數據和電能質量歷史數據訓練控制圖,讓其達到初始穩態。
(3)預測下一時刻的趨勢數據。經過步驟(1)和步驟(2),控制圖已經達到初始穩態。此時如果已知下一時刻的電能質量數據變化趨勢數據,即可計算出控制圖上下控制線,通過對比下一時刻的實測數據和上下控制線的值就能判斷數據是否異常。但是,下一時刻的趨勢數據在當前時刻無法直接獲得,因此需要對下一時刻的變化趨勢數據進行預測。
(4)當下一時刻電能質量數據到達時,檢測數據是否異常,如果正常則更新控制圖。
3.1 電能質量歷史趨勢數據計算
定義(平滑度SD)平滑度描述了二維平面中曲線L上相鄰兩個點之間數值的平均變化量。設L是二維平面上的一條曲線,P=(X,Y)是曲線L上的點,令集合Points={pi,1 ≤i ≤n}是曲線上的n個點,并且pi=(xi,yi),其中xi表示第i 個點的橫坐標,yi表示縱坐標,pi-1、pi、pi+1之間滿足關系式:xi-xi-1=xi+1-xi,則曲線L 的平滑度SD定義如下:

平滑度SD 越小,表示曲線越平滑,當SD=0 時,L退化成為一條水平直線。
雖然電能質量數據變化波動性較大,但數據變化具有一定的特點:如圖4 所示,數據大致呈帶狀分布,數值的增減具有一定的趨勢,并且原始數據在其趨勢線上下均勻分布。因此,數據趨勢線的計算可采用數據平滑的方法。常見的數據平滑算法有中值濾波、均值濾波、高斯濾波、移動窗口最小二乘多項式平滑和滑動平均值平滑[20]等,本文采用滑動平均值平滑法對數據進行平滑,算法如下所示。

圖4 電壓偏差日數據趨勢圖
算法1 數據平滑算法
Input:
souPoints,原始數據集
k,數據窗口大小,k >0
ε,平滑度控制下限,0 <ε <SD(原數據平滑度)
Output:
trendPoints,平滑后的數據集
1.begin
2.SD:=computeSD(souPoints);//計算原數據的平滑度
3.trendPoints=[]
4.while True:
5.if SD <ε:
6. break;
7.for i in range(souPoints.size()):
8. sum:=0;
9. if i <k:
10. for j in range(i):
11. sum:=sum+souPoints[i];
12. mean:=sum/k;
13. trendPoints.add(mean);
14. else if souPoints.size()-i <k:
15. for j from i to souPoints.size():
16. sum:=sum+souPoints[i];
17. mean:=sum/k;
18. trendPoints.add(mean);
19. else
20. for j from i-k/2 to i+k/2:
21. sum:=sum+souPoints[i];
22. mean:=sum/k;
23. trendPoints.add(mean);
24.end for
25.souPoints:=trendPoints
26.SD:=computeSD(souPoints)
27.end while
28.return trendPoints
29.end
在算法中用前k-1個周期的數據與當前時刻的數據的均值來替代當前時刻的數據,其實質是將當前時刻平移k/2個周期。如果k 值過大,則平移的周期較長,平滑后數據與原數據誤差較大,無法作為原數據的趨勢數據;如果k 值較小,局限性較大、平滑效果較低且容易受異常數據的干擾,如極端情況下k 取1 則平滑數據與原始數據一致,通常情況下,k 的取值建議控制在3 至8 之間,具體情況需看數據采樣周期而定。
ε控制著數據的平滑程度,其取值介于0和1倍原始數據的平滑度SD 之間,如果ε 取值太大,則平滑效果不明顯,尤其是數據出現抖動的情況下,容易受抖動數據的影響,不能正確反應數據的變化趨勢;當ε 取值太小時,數據平滑過渡,接近于一條水平直線,無法體現數據的波動性,也不能作為原數據的趨勢數據。通常情況下,ε取值建議控制在0.2至0.5倍原數據的平滑度下。
3.2 傳統控制圖改進及初始穩態訓練
通過對原始數據souPoints的平滑操作,得到原始數據的變化趨勢數據trendPoints。原始數據本身是非平穩的,如果直接用原始數據訓練控制圖可能用盡所有數據最終也無法使控制圖達到穩態,因此,將原始數據和趨勢數據中的每個對應的點進行差值運算得到新的數據集dataSet={}用于控制圖的訓練。差值運算規則如下:
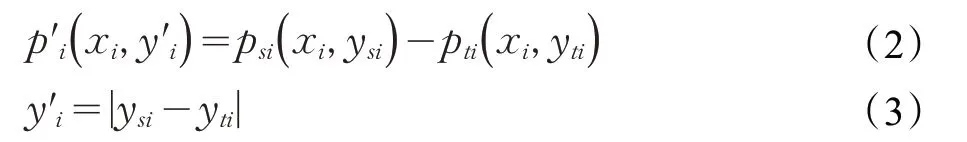
其中,psi和pti分別表示原始數據和趨勢數據的第i 個點。
控制圖的中心線和上下線的確定過程也是穩態控制圖的訓練過程,該過程需要經歷數據分組、統計特征計算、判斷數據是否穩定等過程,求解步驟如下:
(1)準備歷史數據樣本并對樣本進行分組。選取需要分析的某個指標某粒度的歷史數據樣本,數據可分為m 組樣本組(m 的選擇參考文獻[6]中合理子組的選擇),每組數據點數為n(n >2),n的取值取決于分析窗寬。以電壓偏差為例,數據粒度為1 min,分析窗是0.5 h,則0.5 h 內的數據為一組,每組數據點數n=30,假如取25組數據,則訓練樣本的時間跨度是12.5 h。
(2)對每組數據進行統計特征值計算(計算均值Xˉ和標準差S)。計算每組樣本數據的均值和標準差,設共有m 組樣本組,每組數據點數為n,則第i 組樣本點的均值和標準差Si的計算公式如下:
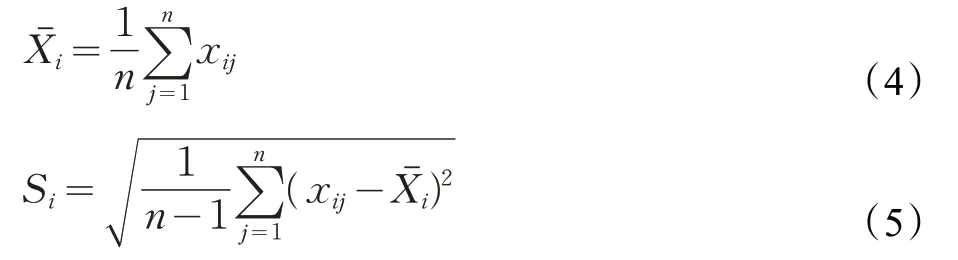
(3)計算S統計控制參數并繪制S控制圖;計算所有樣本組的均值X?和平均標準差Sˉ,公式如下:

計算標準差圖(S 圖)的上控制限(UCL)、中心線(CL)、下控制限(LCL)。差值運算產生的數據具有非負性,并且僅僅需要確定一個數據波動的最大范圍即可完成正常數據范圍的界定,因此只需要求得控制圖的上控制線(UCL)就能確定控制圖的中心線(CL)和下控制線(LCL)。三條控制線的計算公式如下:
其中,系數計算公式如下,當n >25時:
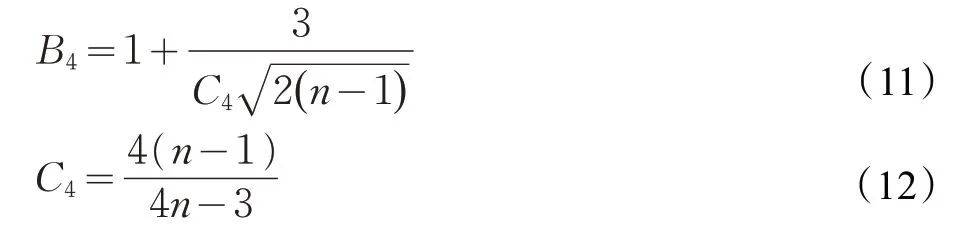
當2 ≤n ≤25,B4取值參見文獻[6]。
(4)在S控制圖上打點,判斷數據是否穩定,如果不穩定則轉到步驟(5),否則轉到步驟(6)。本步驟以及步驟(7)的數據穩定與否的評判標準為:數據處在上控制線或者下控制線以外判定為不穩定,否則判定為穩定。
(5)剔除不穩定樣本數據組,補充備用樣本數據組并回到步驟(2)。

當2 ≤n ≤25 時,A3取值參見文獻[6],當n >25 時,系數計算公式如下:

(7)在Xˉ控制圖上判斷數據是否穩定,如果不穩定回到步驟(5),否則繼續。
(8)形成穩態Xˉ,S統計控制圖。
3.3 電能質量趨勢數據ARIMA預測
ARIMA(Autoregressive Integrated Moving Average model)模型是經典的時間序列預測模型,它包含三個參數p、d 和q,也記做ARIMA(p,d,q),其中p為自回歸階數,d 為差分次數,q 為移動平均階數。ARIMA 模型在預測具備周期性變化規律的數據方面準確率較高。電能質量數據的趨勢數據是本文所提方法的核心數據,趨勢數據能否真正反映數據的變化趨勢對該方法檢測效果好壞起著決定性的作用。結合ARIMA模型和電能質量數據的特點,文章選擇ARIMA 模型進行電能質量趨勢數據的預測。
ARIMA預測的關鍵是確定p、d、q的取值,d 的取值可以通過單位根檢驗(Augmented Dickey-Fuller,ADF)來確定,如果ADF檢驗的結果小于1%、5%、95%置信區間臨界值則當前的差分次數d 就是模型的最終差分次數。p和q的值可以通過計算自相關系數和偏自相關系數并通過觀察它們是拖尾還是截尾來確定,通過觀察通常只能得到p和q的取值范圍,具體的取值需要從p和q的范圍中選擇,選擇的標準是模型的信息準則(Akaike Information Criterion,AIC)值最小。為了降低模型選擇的難度,本文給出了ARIMA模型選擇算法如下。
算法2 ARIMA模型選擇算法
Input:
ts:趨勢歷史數據
P,p的候選值,P={x|x ∈N}
Q,q的候選值,Q={x|x ∈N}
Output:
p,d,q:最優ARIMA模型的三個參數
1.begin
2.dif_n:=0//差分次數
3.isStable:=False//數據穩定標志
4.do
5. adf:=computeADF(ts)//單位根檢驗
6. criVal:=computeCritical(ts)//計算臨界值
7. isStable:=check(adf,criVal)//檢驗數據是否平穩
8. if isStable==False:
9. ts:=diff(ts)//差分
10. dif_n:=dif_n+1
11. end if
12.while(isStable==False)
13.AIC:=INF//初始化AIC為無窮大
14.for temp_p in P:
15. for temp_q in Q:
16. model:=ARIMA(ts,temp_p,dif_n,temp_q)//創建ARIMA模型
17. result:=model.fit()//ARIMA模型訓練
18. temp_AIC:=result.aic
19. if temp_AIC 20. p:=temp_p 21. q:=temp_q 22. d:=dif_n 23. end if 24. end for 25.end for 26.return p,d,q 27.end 由于數據的不斷變化,在進行數據的在線異常檢測過程中,需要不斷地更新控制圖參數。控制圖參數的更新依賴數據異常檢測的結果。當數據被判定為異常時,保持當前控制圖參數不變;當數據被判定為正常時,將差分數據與歷史穩定數據進行合并,并重新計算控制圖的UCL、CL 和LCL,實現控制圖參數的動態更新,更新算法如下。 算法3 穩態控制圖參數動態更新算法 Input: groupSize:歷史穩態數據的組數 ts:新穩態數據 Output: UCLS,CLS,LCLS,UCLXˉ,CLXˉ,LCLXˉ:更新后的控制圖參數 groupSize':新穩態數據組數 1.begin 6.UCLS= 7.CLS=0 8.LCLS=- 9.UCLXˉ= 10.CLXˉ=0 11.LCLXˉ=- 12.groupSize′=groupSize+1//數據組數 14.end 實驗分為兩個部分,第一部分為ARIMA 時間序列預測,通過計算預測結果平均絕對百分比誤差驗證本文預測方法的可用性;第二部分為異常數據檢測結果對比分析。 本文的異常檢測辦法實質上是基于閾值的異常檢測辦法,基于機器學習的檢測辦法和大多數基于數理統計的方法與本文的方法均不屬于一個體系,故本文不作比較。基于云模型的異常檢測方法[4]和基于正態分布的異常檢測辦法(目前項目中使用的方法)都是基于靜態閾值的異常檢測辦法;文獻[21]提出EWMA(指數加權平均)控制圖方法(簡稱EWMA 方法),是控制圖的典型研究成果,它和文獻[19]中的方法都屬于動態閾值方法。本文將本文方法和上述四個方法進行了對比,最后計算各自方法的查全率和查準率驗證本文方法的有效性。 準確的預測數據的變化趨勢是實現數據異常檢測的關鍵。本文選取河南某監測點電壓偏差、電壓有效值等多個指標一個月的數據進行預測對比,圖5 為電壓偏差(左圖)和電壓有效值(右圖)的某一天的預測結果對比圖(由于預測結果與原始數據較接近,為了區分原始數據和預測數據,故采用雙坐標軸分別展示,左坐標軸均代表原始值,右坐標軸均代表預測值),其中電壓偏差和電壓有效值預測平均絕對百分比誤差分別為1.54%和3.29%,預測結果較好。 圖5 電壓偏差和電壓有效值ARIMA預測結果對比圖 實驗數據為河南省某監測點2018 年6 月15 日的數據。選取的指標有電壓偏差、電壓有效值、零序電壓、電壓總諧波畸變率、基波電流有效值等。由于篇幅有限,本文只對電壓偏差和零序電壓實驗結果進行展示。 圖6 為電壓偏差數據和零序電壓數據散點圖,其中零序電壓數據中正常數據441 個,異常數據39 個;電壓偏差數據中正常數據1 060 個,異常數據380 個。針對上述數據,實驗分別采用前文提到的四種方法以及本文方法對測試數據進行異常檢測,其中圖7 為五種異常檢測辦法分別對電壓偏差和零序電壓進行檢測的結果,左圖為電壓偏差檢測結果,右圖為零序電壓檢測結果;表1為五個模型檢測結果,表2 為五種檢測方法對測試數據進行檢測的對應的查全率和查準率。 圖6 測試數據集 圖7 電壓偏差和零序電壓下五種方法檢測結果對比 從圖7 和表1、表2 的對比結果可以看出,云模型和正態模型判定異常時都以某一個固定的閾值作為異常判定標準,沒有充分考慮數據的波動是正常波動還是異常波動,沒有充分考慮到時序數據的變化趨勢,導致把本該判定為異常的數據也判定為正常,本該判定為正常的數據反而判定為異常,檢測結果較差;周期模型雖然是動態閾值檢測方法,但是如圖8 所示,相較于本文提出的方法產生的趨勢數據,周期模型的產生趨勢數據受異常數據影響較大,最終導致波動性較大,不夠平滑,無法真正描述原始數據的變化趨勢,因此檢測結果較差;EWMA 模型雖然也考慮到動態調整閾值,但是該方法也只是微調控制圖上下線,并未從根本上突破傳統控制圖的限制,針對本文這種波動范圍較大的數據,檢測結果仍然較差。本文提出的方法充分考慮了時序數據的變化趨勢,并且在更新控制圖參數的過程中動態地改變異常值判定閾值,能很好地適應數據的變化趨勢,檢測結果較好,無論是查全率還是查準率都較高,在針對具有周期性變化規律并且波動范圍較大等特征的數據的異常值檢測方面具有較大的優勢。 表1 三種方法異常檢測結果 表2 三種檢測方法查全率、查準率對比 % 圖8 周期模型和本文模型趨勢數據對比 本文針對常規的異常數據檢測方法無法有效檢測變化范圍較大且具有周期性變化規律特征的電能質量異常數據的問題,將傳統控制圖的控制線化曲為直并結合時間序列預測方法,提出了基于控制圖和動態閾值的電能質量異常數據在線檢測方法。實驗證明該方法針對具備波動范圍較大且具有周期性變化規律的時序數據的異常檢測效果較好。 本文方法準確檢測出異常值的前提是能準確地預測數據趨勢的變化。為了保證預測的準確性,本文采用每次進行趨勢數據預測前都重新訓練ARIMA模型的方法,雖然這種方法預測準確性較高,但是這種方式存在潛在的性能問題:通常P、Q 的參數取值較少,模型可以正常工作,但是當給定的參數P、Q 取值較多時,訓練模型的時間成本增大,可能造成數據堆積,本文希望在以后的研究中對其進行改進。3.4 電能質量異常數據檢測及參數更新
4 實驗效果評價
4.1 ARIMA時間序列數據趨勢預測

4.2 異常數據檢測結果對比

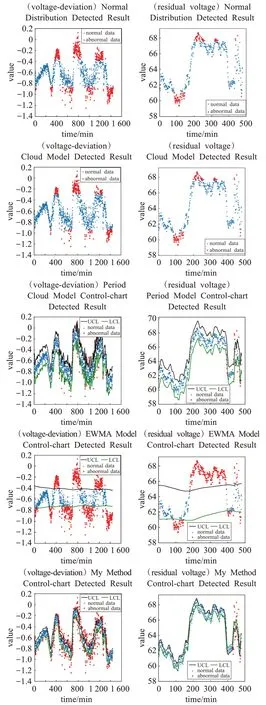
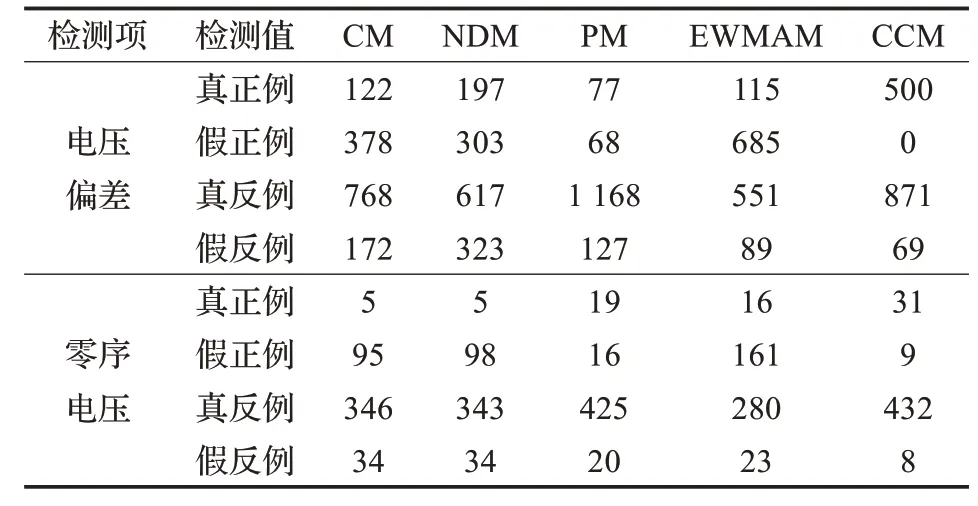
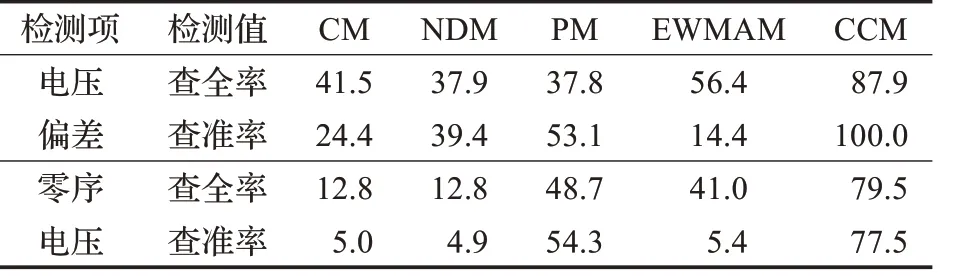

5 結論

