基于視覺感知的圖像放大

杜宏偉，喬美麗，宋 剛，張云峰，包芳勛

1.山東財經大學 計算機科學與技術學院，濟南250014

2.山東省數字媒體技術重點實驗室，濟南250014

3.山東省教育招生考試院，濟南250011

4.山東大學 數學學院，濟南250100

1 引言

圖像放大是指由低分辨率（Low Resolution，LR）圖像通過插值獲得高分辨率（High Resolution，HR）圖像的一種圖像處理技術[1]。從信號角度來說，插值是一個離散采樣點與插值核函數卷積的過程，如果一個信號是帶限信號，則此信號可以完全由采樣信號利用理想濾波器sinc 函數重建[2]，但是sinc 函數只能通過近似來實現。早期的插值算法如最近鄰插值、雙線性插值、雙三次插值[3]和三次樣條插值[4]等都是近似sinc 函數，它們相對簡單且易于實現，但重建后的圖像會出現不同程度的鋸齒和模糊現象。

為此，學者們做了更深入的研究。一般來說，插值算法大致可分為離散方法和連續方法兩類。離散方法是指利用已知像素點通過某種變換確定未知像素點。文獻[5]提出一種新的邊緣指導的圖像插值方法（New Edge-Directed Interpolation，NEDI），該算法根據LR 與HR協方差系數的幾何對偶性計算出插值函數中的權重系數，從而求出未知點的像素值。文獻[6]提出一種基于多方向濾波和數據融合的圖像插值方法（an edgeguided image interpolation algorithm via Directional Filtering and Data Fusion，DFDF），將每個待插點的鄰域分成兩個觀測子集，并從正交的兩個方向估計待插點的灰度值。文獻[7]提出了一種基于軟決策的圖像插值方法，其參數和數值估計采用最小二乘法。文獻[8]提出一種邊緣指導圖像插值方法，利用泰勒級數展開的近似方法，對于待插像素點沿其四個方向估計像素值。基于非局部幾何相似性和方向梯度，文獻[9]對周圍像素點加權平均確定插值點像素值，根據正則化最小二乘法確定權重系數。以上這些算法能較好地保持插值圖像的空間相關性，且具有良好的主觀視覺質量和圖像客觀質量評價值。但是，這些圖像插值算法主要基于離散思想，不能夠對圖像進行任意倍數的放大，而且與傳統的方法相比，時間復雜度相對較高。雖然這些插值算法能夠把圖像邊緣部分處理地較好，但是在細節部分會出現走樣、噪聲等現象。

連續方法是指將圖像離散采樣數據轉換為連續的灰度曲面，然后確定未知像素點。文獻[10]提出了一種基于分段常張力基樣條的插值方法，與傳統的三次樣條方法相比，它可以有效避免圖像出現振鈴現象。文獻[11]使用圖像數據作為約束構造擬合曲面來還原采樣過程。基于構造的有理插值函數，文獻[12-15]提出的插值模型能夠很好地刻畫圖像的結構，可以在插值數據不變的前提下通過調整參數獲得更好的圖像質量，此類方法能夠有效保留圖像的細節信息。

近年來，深度學習作為人工智能方面的一個重要分支，得到人們的廣泛關注。目前基于學習的方法主要分為兩類：一類是基于圖像自身的學習，一類是利用圖像外部信息的學習。前者根據圖像的自相似性進行圖像重建。將稀疏編碼與深度學習方法相結合，文獻[16]提出了一種基于深度卷積神經網絡的圖像超分辨重建算法（Cascaded Sparse Coding Network，CSCN）。此算法利用圖像自身的相似冗余信息，避免了圖像出現人工痕跡，但若LR中沒有足夠的冗余信息，此類算法會導致細節丟失。后者借助附加的圖像庫的信息進行圖像重建。文獻[17]通過端到端的方式學習LR 圖像與HR 圖像之間的映射關系，提出了一種基于全卷積神經網絡的超分辨率算法（Super-Resolution Convolutional Neural Network，SRCNN），提高了重建效果。然而，該算法的重建效果取決于的訓練的圖像庫，且訓練時間較長。

圖像插值實際上是一個主客觀（人眼視覺感知和圖像）相統一的過程。根據人眼視覺感知特性，人眼更關注于圖像的邊緣區域而非平滑區域。文獻[18]提出了一種基于人眼對比敏感度的圖像增強算法，通過單一參數對圖像局部梯度的調節來增強局部圖像對比度。將對比度增強視為最優化問題，通過感知約束最大化圖像的平均局部對比度，文獻[19]提出了一類新的人類視覺系統（Human Visual System，HVS）指導的以神經網絡為技術支撐的自適應插值方法。根據HVS 的特征建立了一個模糊決策系統，把輸入圖像的像素分為人眼感知敏感類和非敏感類，不同的區域使用不同的插值手段。但此方法的局限性在于圖像像素的劃分方法與所用的插值方法不一致，這樣可能導致圖像內在的自然屬性（非線性、多尺度特性、方向性）遭到破壞。在插值過程中，如果把人眼視覺特性、圖像區域劃分、圖像插值等融合在一個模型中，最大化保護圖像自然屬性，具有重要的理論意義。

本文把圖像插值與人眼視覺感知相結合，提出了一種自適應視覺感知的圖像放大方法。根據圖像結構，構造一類新的含有可調參數的有理函數插值模型，當形狀參數都取1 時，此有理插值模型退化為多項式插值模型。該模型通過調節形狀參數，可以獲得最佳的插值曲面。基于本文構造的模型進行圖像插值，首先利用等值線方法將輸入圖像自適應地劃分為邊緣區域和非邊緣（平滑）區域。然后，在圖像結構簡單且人眼關注度低的平滑區域，采用多項式模型插值；在圖像結構復雜且人眼關注度高的邊緣區域，采用有理模型插值，其形狀參數根據人眼視覺感知特性進行自適應調節。最后，獲得高質量的插值圖像。

2 插值模型

2.1 雙變量有理插值函數

令f(x,y)為平面區域Ω:[a,b;c,d]上的雙變量有理插值 函 數，{(xi,yj,fi,j),i=1,2, …, n, n+1j;=1,2,… ,m,m+1}為Ω 上給定數據點集，fi,j=f(xi,yj)。對xy 平面上任何點 (x,y)∈[xi,xi+1;yj,yj+1]，hi=xi+1-xi，θ=(x-xi)/hi，lj=yj+1-yj，η=y-yj/lj，對每個y=yj,j=1,2,… ,m+1，構造x方向的插值曲線：

其中αi,j＞0，且

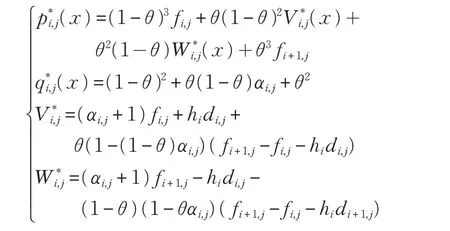
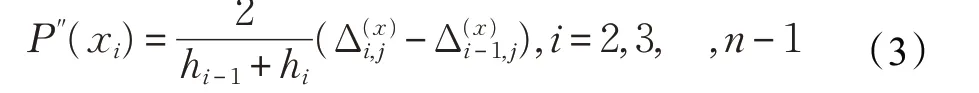
在節點x1和xn處，偏導數定義為：

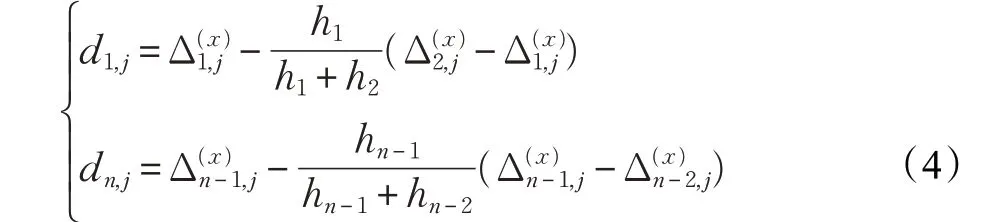
對每個點對(i,j);i=1,2, …,n-1和j=1,2, ,m-1，使用x 方向的插值函數(x)來定義上的有理插值函數Pi,j(x,y)如下：

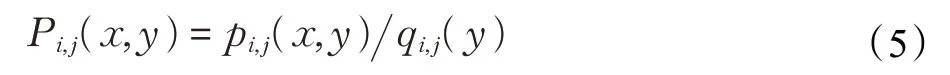
其中

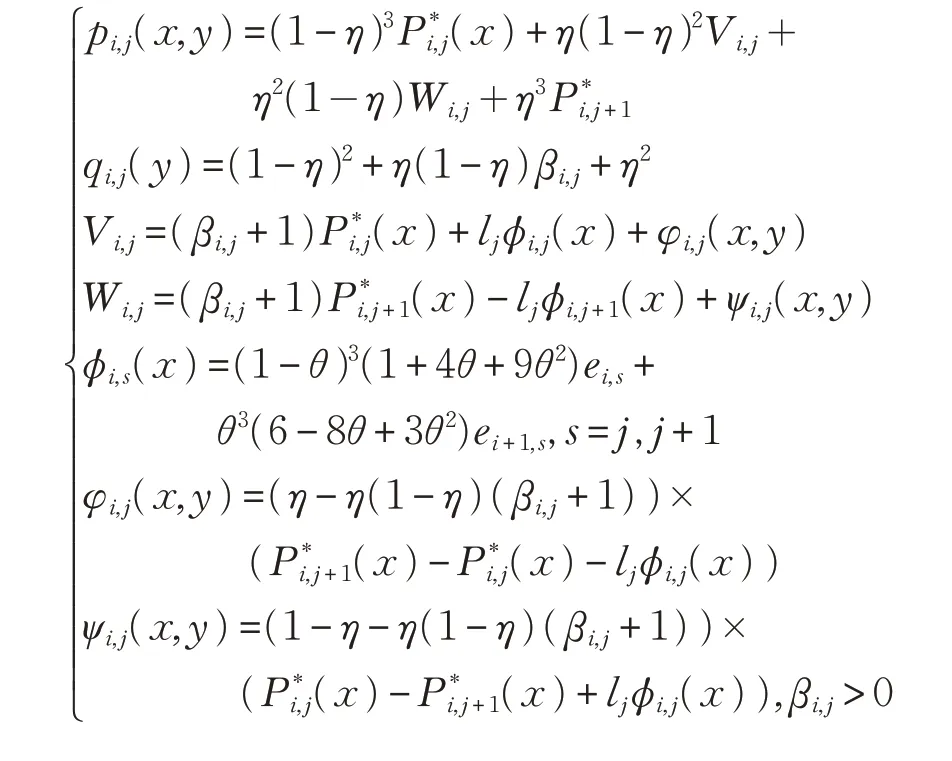
該插值函數由插值數據和形狀參數確定，形狀參數取值不同，表達形式也不相同，特別地，當αi,j=βi,j=1時，該模型退化為多項式插值模型。

圖像可視為二維平面上的等距節點數據。給定一幅m×n的圖像Im,n，fi,j(0 ≤i ≤m-1,0 ≤j ≤n-1)是Im,n內坐標為(i,j)的像素值，目的是得到圖1 中紅色像素點所在面片的數學表達式，從而確定圖像中的任一點fi,j的像素值。

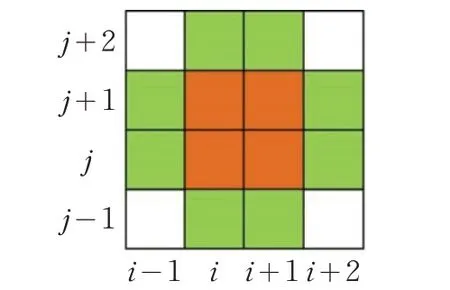
圖1 有理插值模型

如圖1 所示，根據公式（5）定義的插值函數Pi,j(x,y)，給 定12 個 像 素 點 fi,j-1，fi+1,j-1，fi-1,j，fi,j，fi+1,j，fi+2,j，，fi,j+1，fi+1,j+1，fi+2,j+1，fi,j+2，fi+1,j+2，可以構造一個過4個像素點fi,j,fi+1,j,fi,j+1,fi+1,j+1的矩形面片。

2.2 插值函數的性質

性質1 設Pi,j(x,y)為定義在[xi,xi+1;yj,yj+1]上的有理插值函數，對于任意的正參數αi,j和βi,j，則

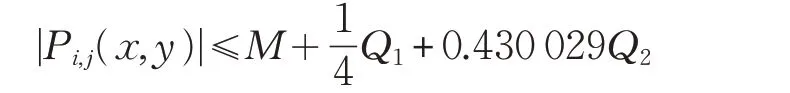
定理1 設為等距節點，即hi=(b-a)/n。若參數 βi,j滿 足 βi,j=βi+1,j,i=1,2,… ,n-2，則 插 值 函 數Pi,j(x,y)在插值區間[x1,xn;y1,yn]上C2連續。

公式（5）定義的插值模型含有形狀參數，插值曲面的形狀可以通過形狀參數來調節。但性質1 給出了曲面的有界性質，即無論參數如何調整，曲面的變化都被約束在邊界內。考慮到圖像灰度值[0，255]的限制，所以在調整曲面的過程中，曲面要同時滿足邊界約束和灰度范圍限制。與C1連續的有理插值函數相比，本文構造的C2連續有理插值函數在插值面片的內部和拼接處光滑性更好，可有效保持插值圖像清晰的邊緣結構。

2.3 人眼視覺感知特性

人眼對于空間不同對比度的敏感度符合韋伯定理。韋伯定理是指感覺的差別閾限與標準的刺激強度之比是一個常數。令C 為局部對比度增強閾值，?C 表示對比度感知變化，超出差別閾值，則?C 和C 滿足：

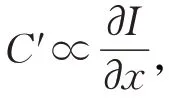
基于韋伯定理，通過自適應調整公式（5）中的參數α,β 來改變曲面的梯度。插值區域的平均梯度表示為δ，若插值區域像素變化劇烈，δ就越大，意味著圖像梯度變化也越大。面片梯度grad( Pij( x,y ))表示為：

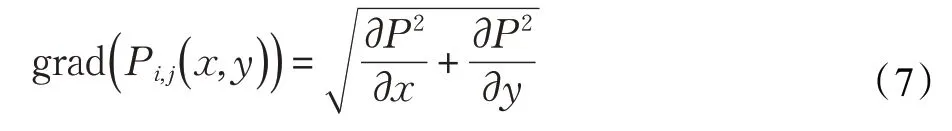
由以上公式可知，曲面的拉伸程度與曲面的梯度成正相關非線性關系。人類的視覺適應具有S 型非線性特點，通常用Sigmoid 函數來刻畫[20]。Sigmoid 函數模型如下

其中，? 為最大值和最小值的差值，μx為S函數在x軸上的偏移，k 表示邊緣的傾斜程度，μy為S函數在y 軸上的偏移。如圖2 所示，Sigmoid 函數滿足人眼視覺特性且具有非線性[21]，用它來表示δ與grad(Pi,j(x,y))的非線性、正相關關系。

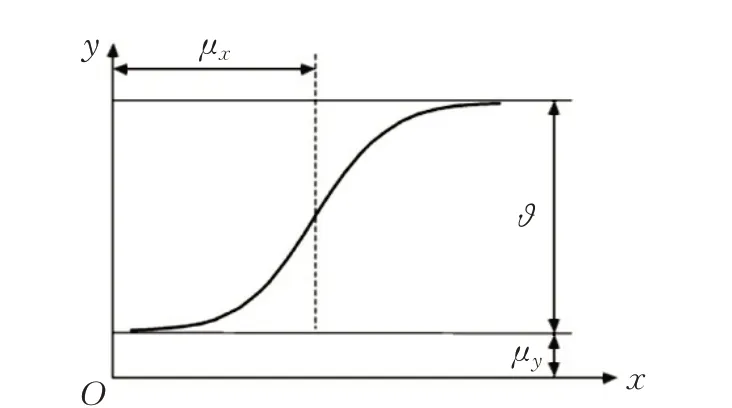
圖2 Sigmoid型函數模型

3 本文算法

用等值線方法對圖像進行邊緣檢測，檢測出來的平滑區域結構相對簡單，采用多項式模型插值；邊緣區域結構復雜，基于人眼對比敏感度準則對公式（5）自適應調整αi,j和βi,j。

3.1 自適應區域劃分

目前，經典的邊緣檢測方法如Roberts算子、Laplace算子等可以利用圖像梯度將圖像的邊緣檢測出來。但是，Roberts 算子對圖像邊緣附近的區域內產生較寬的響應，不能有效檢測到圖像的高頻細節，處理后圖像缺失細節信息；Laplace 算子對孤立像素的響應比對邊緣或線的響應更強烈，所以處理后圖像會產生很多孤立點。以上檢測方法的結果不能很好地反映圖像的自然屬性。本文根據構造的插值模型來選擇邊緣檢測方法，實現了圖像劃分與圖像插值的有機統一，最大化保護圖像的自然屬性。

根據等值線繪制原理，對每個插值單元繪制等值線。插值單元指圖1 中由[ ]i:i+1;j:j+1 圍成的矩形（即紅色像素點圍成的矩形）。存在等值線的插值單元為邊緣區域，否則為平滑區域。區域檢測的閾值應能概括描述該插值單元的灰度信息，且信息相關性最大，所以選取插值單元上的4個像素點及其四鄰域點共12個像素點的均值作為自適應區域檢測的閾值，即自適應檢測閾值為：

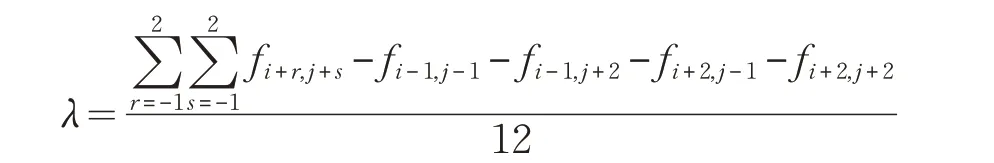
令Δxm,n=fm,n-λ,m,n=0,1，根據等值線繪制原理，若Δxm,n是同號，則此插值單元屬于平滑區域，反之屬于邊緣區域。因此，可以利用等值線方法對圖像進行區域劃分。如圖3 所示，若在一個插值單元中四個頂角符號不同，則該插值單元屬于邊緣區域。圖3（a）中Δxm,n表示一個插值單元中對應的四個頂點。（b）～（e）表示在一個插值單元中四個頂點的符號不同時的邊界檢測結果。圖4 為圖像邊緣檢測結果。其中，（a）是原圖像，（b）～（d）分別是圖像用等值線方法、Laplace算子和Roberts算子的邊緣檢測結果。可以看出，等值線方法可以有效地檢測到圖像的紋理和邊界。

圖3 基于正負號的紋理檢測

圖4 圖像邊緣檢測結果

3.2 圖像插值

對于平滑區域，采用多項式插值模型。對于邊緣區域，采用有理插值模型，形狀參數根據人眼視覺敏感度自適應設置。

當α 和β 都等于1 時，公式（5）就變成了多項式插值，表達式如下：

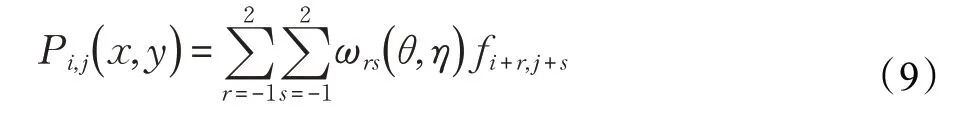
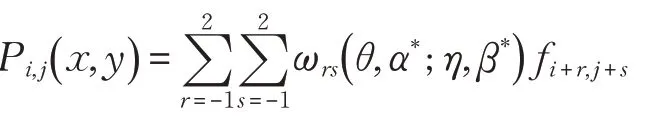
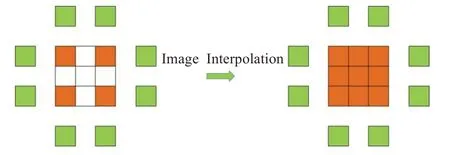
圖5 圖像插值示意圖

單元周圍12 個像素點構造出該插值單元的曲面，確定插值點的灰度值，右圖為圖像插值后的示意圖。

3.3 基于人眼視覺感知的參數自適應調節

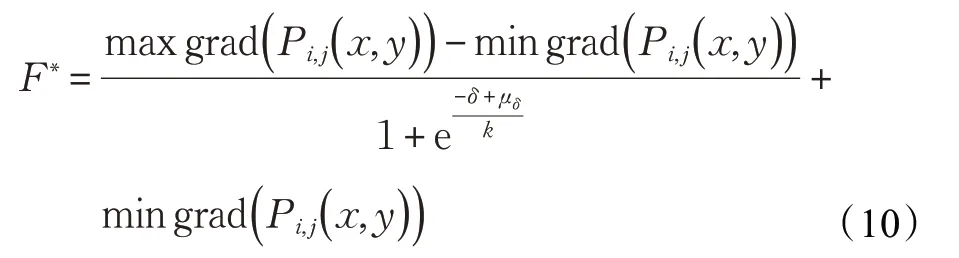
其中，k 代表此S 型函數的陡峭程度，μδ代表S 型函數向δ 軸 正 方 向 移 動 的 距 離，max grad( Pi,j( x,y ))和min grad( Pi,j( x,y ))分別表示梯度的最大值和最小值。在2×2 的面片上，數值計算每一個像素點的梯度值，由此確定對應最大、最小梯度值所在像素點的曲面坐標，將相應坐標代入插值函數，即可得到max grad( Pi,j( x,y ))、min grad( Pi,j( x,y ))。此時，F?是一個關于α、β 的二次函數，其值是S型函數在梯度最大時的函數值。由曲面的有界性可知，一張面片的插值函數在閉區域上梯度有界。最后，根據F?的值確定α?、β?的取值。2×2面片上四個像素點梯度的數值計算公式為：

其中，G(r,s),r=i,i+1,s=j,j+1為像素點在(r,s)處的梯度值。

若在點( x?,y?)處Pi,j( x,y )取得最大值Pi,j?( x,y)，且要 重 新 定 義 為 ：

圖像的信息熵反映了圖像包含的信息量，圖像的信息熵越大，圖像的對比度就越高，圖像的視覺效果就越好，從表1 中可以看出，基于人眼視覺感知對形狀參數調節后，圖像的信息熵變大，圖像的視覺效果提高。

4 實驗

實驗選取9 幅標準測試圖像，如圖6 所示。采用隔行隔列下采樣，選取具有代表性的算法bicubic、NEDI[5]、DFDF[6]、RSAI[7]、SRCNN[17]、CBI[22]、DCCI[23]、A+[24]與 本文算法進行比較。下面主要從主、客觀效果和時間復雜度3個方面來測試本文算法的效果。

表2 給出了不同插值算法的客觀評價數據：峰值信噪比（Peak Signal To Noise Ratio，PSNR）和結構相似性（Structural Similarity Index，SSIM）。從表1 可以看出，與其他方法相比，本文提出的方法擁有最高平均PSNR和SSIM值，具有較強的競爭力。

表1 形狀參數自適應調節后圖像信息熵值比較

圖6 標準測試圖像

圖7 ～圖11 提供了各插值算法的視覺效果比較，并將局部細節放大顯示。其中，圖7 和圖8 突出顯示了不同算法對圖像邊緣區域的重建效果，圖9、圖10 和圖11展示了對圖像紋理細節區域的刻畫效果。如圖7 所示，由bicubic、A+、SRCNN 重建的圖像出現了嚴重的鋸齒現象，RSAI、ICBI、DCCI和DFDF方法出現了模糊、鋸齒現象，本文算法和NEDI有效保持了圖像邊緣的光滑性。如圖8 所示，bicubic 出現了邊緣模糊現象，NEDI 算法出現了斑點噪聲，RSAI、A+和SRCNN 算法產生了不連續的條紋，ICBI 也出現了邊緣失真現象，其余各算法保持了清晰的邊緣。在處理圖像紋理細節方面，如圖9 所示，NEDI、RSAI、ICBI、DCCI 都出現了嚴重的扭曲變形、紋理錯亂現象，DFDF 算法也丟失了圖像細節信息，A+和SRCNN 出現了紋理變形、噪聲現象，不能有效保持圖像的結構特征，本文方法有效地保持了圖像的結構特征。從圖10 可以看出，本文算法較好地恢復了圖像的細節，其余算法出現了不同程度的細節扭曲現象。圖11 是Barbara 圖像的局部細節展示（圖6 紅框標注的部分），從對桌布、桌腿等細節的重建效果來看，本文算法的視覺效果最好。因此，從圖像細節的刻畫效果來看，本文算法優于其他算法。

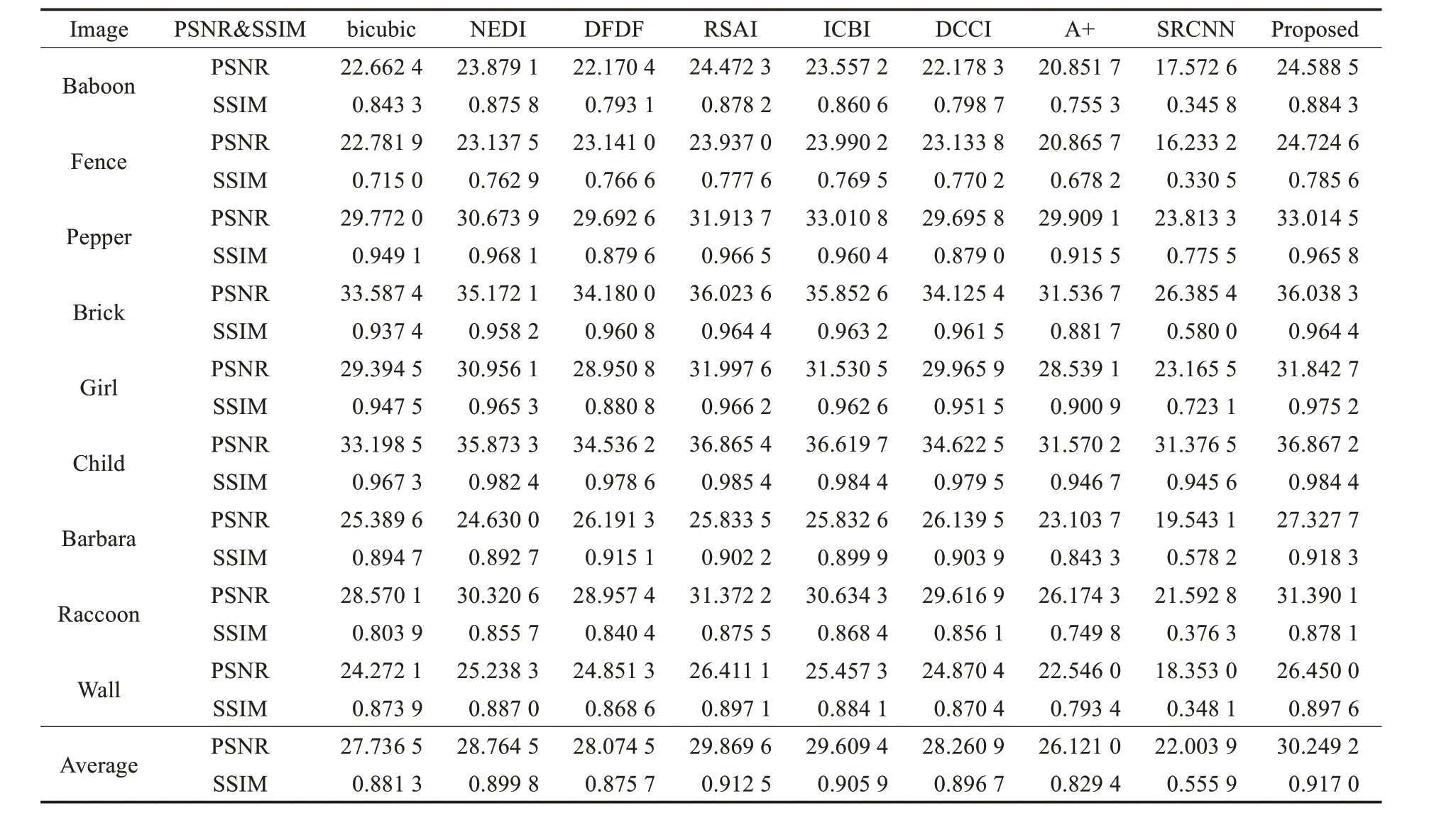
表2 不同方法的PSNR和SSIM值比較

圖7 不同算法Girl對比圖

圖8 不同算法Fence對比圖

圖9 不同算法Wall對比圖

圖10 不同算法Raccoon對比圖

在實際的應用中，不僅要求獲得好的圖像質量，同時，圖像的處理速度也是非常重要的。從理論上分析，本文方法對一個插值面片進行插值包括自適應區域劃分，構造插值模型，形狀參數確定，它們都是簡單的代數運算，時間復雜度是O(1)。對于一個m×n大小的圖像，插值面片有(m-3)×(n-3)個，整幅圖像遍歷一遍時間復雜度是O(m×n-3m-3n+9)，所以本文算法總的時間復雜度是3×O(1)×O(m×n-3m-3n+9)≈O(m。×n)上述分析可以看出，本文算法的時間復雜度與多項式插值算法處于同一量級。如表3 所示，本文算法在保證圖像質量的情況下，擁有較低的運行時間。

圖11 不同算法Barbara對比圖

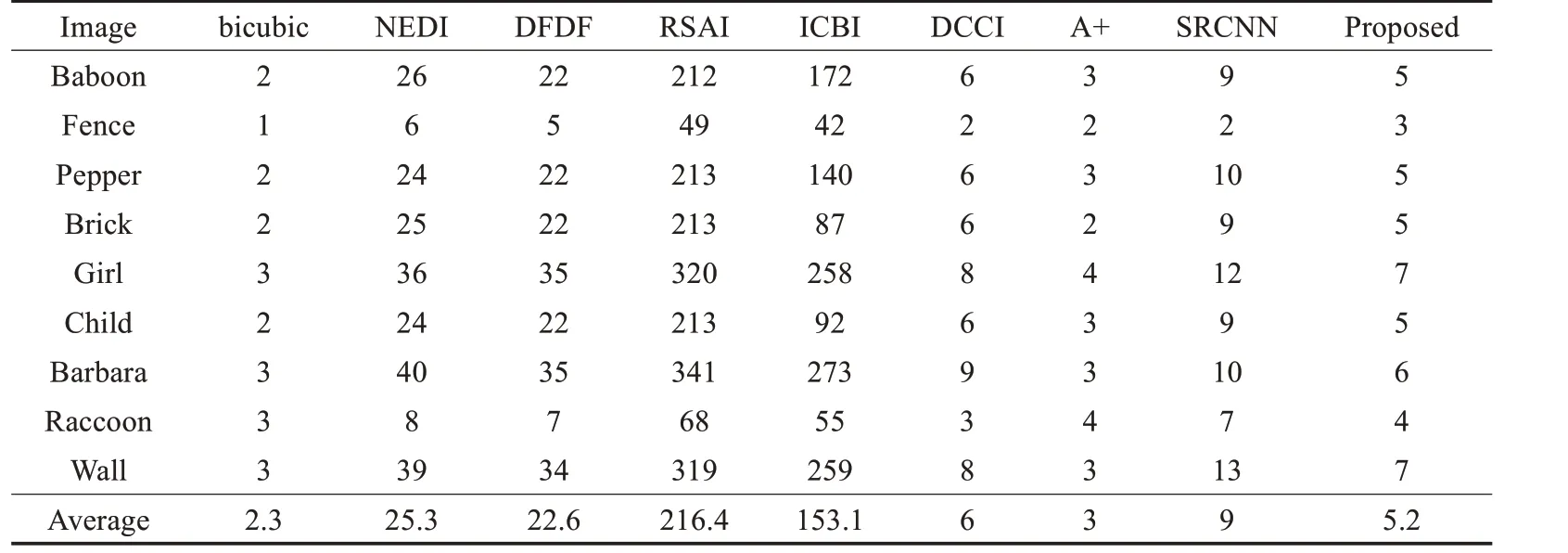
表3 不同插值算法運行時間對比s

基于以上分析，bicubic總體上插值效果不及其他插值算法，尤其在圖像的邊緣區域。NEDI 算法是基于邊緣指導的插值算法，此方法可以保持圖像清晰的邊緣結構，而在處理紋理細節較多的區域時，會導致紋理扭曲、變形或產生噪點。DFDF 算法不會使圖像的紋理細節扭曲變形，但是視覺效果不理想，尤其在圖像的非邊緣區域容易出現細節信息丟失現象。RSAI算法在一定程度上保持了圖像的細節信息，而在圖像的邊緣區域容易產生鋸齒現象。ICBI 算法可以獲得較高的客觀評價數據，但在圖像的紋理細節區域容易出現扭曲變形現象。DCCI 算法對圖像邊緣區域的重建效果較為理想，在圖像的紋理細節區域也容易出現扭曲變形現象。A+和SRCNN 算法的重建效果依賴于訓練圖像庫，當測試圖像與訓練圖像不屬于同一類圖像庫時，容易產生紋理失真，邊緣鋸齒現象。相對于上述算法，在視覺效果上，本文算法保持了圖像原有的結構信息，在客觀數據方面，PSNR提高了0.37～8.24 dB，且時間復雜度較低。

5 結束語

基于構造的雙變量有理函數插值模型，本文提出了一種自適應視覺感知的圖像放大算法。利用人眼視覺感知規律，對插值函數的形狀參數進行適應性調節，實現最優插值。根據等值線繪制原理，提出等值線方法來檢測圖像的邊緣信息，基于構造的插值模型選取邊緣檢測的閾值，將區域劃分與圖像插值融合在一個模型里，最大化保護圖像的自然屬性。因構造的插值模型具有簡單的顯性表達式，本文算法具有較低的時間復雜度。實驗證明本文算法取得較好的主客觀效果。