“童畫”釋義，讓概念內涵看得見

李艷梅

[摘要]數學概念教學中，由于教師忽視概念命名的“講理性”，導致學生不知概念為什么命此名而不命彼名，及命此名比命彼名好在哪里。在概念教學中，采用“童畫”釋義的方式，可讓概念內涵看得見，有效促進概念教學質量提升。

[關鍵詞]童畫;概念內涵;命名;看得見

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2020）11-0049-02

數學概念是數學知識表征的形式之一。在數學概念教學中，教師應重視概念建構過程，力求最大限度地讓學生理解、感悟、概括概念的本質屬性。

采用“童畫”釋義的方式，讓學生明白概念為什么命此名而不命彼名，或者讓學生通過對關鍵字詞進行理解、比較、辨析，體會到命此名比彼名更好，這樣才算是徹頭徹尾的“講理”，學生對概念的理解也才是多維度的、多層次的，對概念的學習也才是可持續的。

一、顧名思義，“童畫”釋義，激活數學直覺明理

在教材中，有不少知識板塊的概念教學是以類屬關系呈現的，即先學習上位概念再學習下位概念。如蘇教版教材四年級上冊“角的認識”單元，在學習角的認識與度量之后才學習角的分類。當學生學習角的分類時，更側重于下位概念在上位概念中的同化。因此，在教學這一內容時，可以把概念的形成融在對概念名稱的釋義中。

【案例一】

師：通過上節課的學習，我們知道根據角的大小形狀可把角分成直角、銳角、平角、鈍角、周角。請大家根據角的名稱猜想每種角是什么樣的，說說自己的感覺，并拿出活動角操作一下。

生1：我感覺平角的樣子應是平平的。（操作活動角，如右圖）

師：為什么有這樣的感覺？

生1：平角的“平”字說明這種角的樣子是平平的。

師：大家畫一個平角，并量一量它是多少度。（學生畫出平角并匯報平角是180°）

生2：我覺得周角是角的一條邊轉動一周后彤威

的角。（操作活動角，如右圖）

師：大家通過活動角來演示一個周角并想想周角是多少度。

生3：我通過測量知道周角是360°。

生4：在轉動活動角的一條邊時，其實出現了兩個平角，所以周角是360°。

師：平角和周角的度數是一個定值。平角是180°，周角是360°。

生5：我覺得銳角的角比較尖。

師：你怎么想到銳角比較尖呢？

生5：因為銳角的頂部像刀尖。

師：“銳”表示什么意思？

生5：尖銳、銳利。

師：可見銳角的樣子真是尖尖的。大家都來用活動角制作一個銳角。請把自己制作的銳角畫在本子上，并量一量它們的度數。

（學生自由操作，并匯報各自所畫銳角的度數）

師：同樣是銳角，度數卻不同，你有什么想法？

生6：銳角的度數不全是同一個度數。

生7：銳角的度數有大有小，但都沒有超過180°。

生8：銳角度數不超過90°。

師：平角和周角都是一個固定的度數，而銳角的度數也在一定的范圍內。銳角應該是低于哪個度數呢？

生9：應該低于90°。

師：90°的角就是直角了。為什么把90°的角稱作直角呢？操作活動角看看。（學生操作后交流）

生10：我感覺當直角的一條邊是橫線時，另一條邊就是豎線。

師：你想到哪個詞？

生10：我想到“橫平豎直”這個詞。

師：如果把一條邊橫著放，另一條邊則是豎直的，這時直角的兩條邊的狀態就是橫平豎直。

“透過現象看本質是數學學習的精髓。”而引導學生領悟則是教師教學的關鍵。上述教學中，教師借助“童畫”迅速表征每種角的形狀差異，盡管沒有分析與綜合的過程，但個性的感知與表達已經讓角的不同特征深深地印在學生腦海中。在命名極具形象性的同級概念時，可以充分發揮學生的數學直覺，使學生形成“第一印象”，讓每個概念的本質與關鍵在學生的學習伊始就扎下根基。

二、望名究義，“童畫”詮釋，利用數學自覺析理

善于思考問題并提出問題，是自覺學習的重要表現之一。學生長期處于被動接受狀態時，就容易形成懶性思維。因此，應培養學生學習的自覺性。當學生“勇敢”提出問題時，教師既要充分肯定問題的價值，更要對其做出深度回應，并通過多種方式進行“講理”，以化解學生心中的“惑”。而要做到這一點，教師可采用“童畫”釋義的方式。

【案例二】

在引導學生做正比例和反比例的練習時，一學生突然提問：“我覺得反比例不像比例，怎么還說它是反比例呢？”解決這個問題不僅有利于鞏固正、反比例的意義，還可以強化正、反比例間的內在聯系。因此，筆者組織學生先討論再用圖示表示正比例和反比例之間的關系。

師：從字面上來看，正比例的“正”應該怎樣理解？

生1：我認為“正”是“真正”的意思，正比例是真正的比例。

生2：也可以理解為“正宗”，那正比例就是正宗的比例。

生3：正比例既然是比值相等的兩種量，兩組不同的對應量組成的比例就是正確的，我認為“正”可以理解為“正確”。

師：請試著從正比例的意義中找到“正”的含義。

生4：在正比例中，相關聯的兩種量，比值一定，就是說兩種量同時擴大，或同時縮小，變化是一致的。

師：這樣也可以說是變化方向相同。

生5：正比例中兩種量的變化相同，所以就稱它為正比例了。

生6：是不是因為相同才稱為“正”，就像以前學過的等邊三角形也稱為正三角形，四條邊和四個角均相等的四邊形稱為正方形。正比例中兩種量的變化方向是相同的。

師：你說的都很有道理，也很有說服力！那反比例的“反”又該怎樣解釋呢？

生7：反比例的“反”可以理解為“不是”，反比例就是“不是比例”。

生。：反比例可以稱為非比例，“非”是是非的“非”。

師：大家借助工具書查查“反”有沒有“不是”“非”的意思。

（學生查工具書后，一致認為“反”是顛倒、方向相背（跟“正”相對）的意思）

生9：因為反比例中兩種量的變化方向相反，所以稱它為反比例。

生10：反比例與正比例是相對的。

師：說得好！那反比例是不是比例呢？

生11，：不是比例，它正好與比例相反，所以才叫反比例。

師：正好與比例關系相反的數量關系，我們起名為反比例是相當合適的。

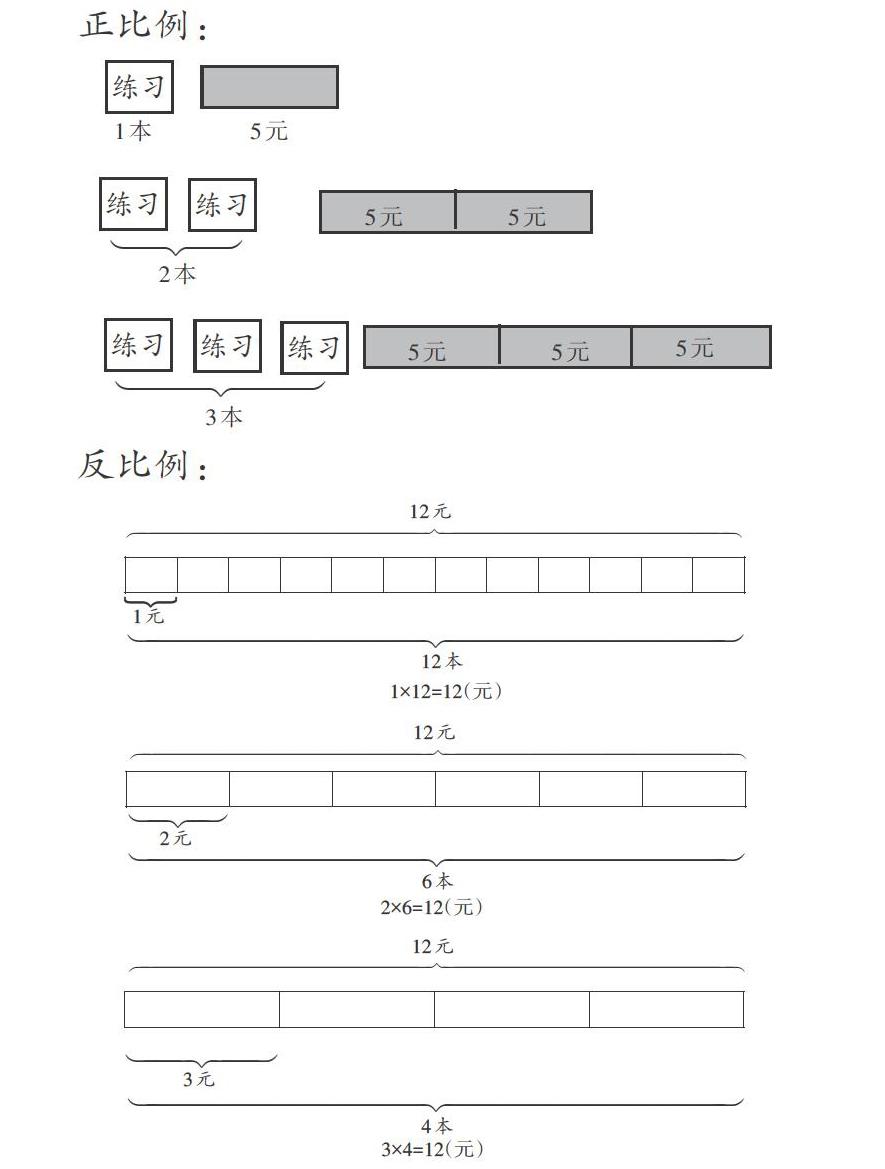
正比例：

反比例：

明確正、反比例的意義，與真正建構正、反比例數學模型是不能完全等同的。因為抽象化的數學語言可以背出來，但并不意味著能把這種語言轉化成數學性的思考。上述案例中，教師先引導學生對正、反比例中“正”“反”的意思進行理解，再利用“童畫”釋義，是對學生數學自覺的因勢利導，也是對數學模型建構的加固催成。

概念學習過程“既不能依賴于對幾個例子的邏輯推演，也不能異化為對個別詞語的理解與合成過程”。因此，概念學習絕不能把對概念命名的濃縮過程當作概念學習的核心內容，也不是所有概念的學習都需要經歷命名過程。不過，通過“童畫”釋義的方式，把概念內涵外顯出來，有助于概念的嚴密表達和真正建構。

【本文系徐州市教育科學“十三五”規劃課題“數學‘童畫，讓兒童的思維過程看得見”的實踐研究（立項號：GH-13-L227）階段性成果。】

（責編黃春香）