用于單相組合式同相供電的CPD結構可靠性研究

王久琿,王 果,2,周子軒,王 繁,田銘興,2

(1.蘭州交通大學自動化與電氣工程學院,蘭州 730070； 2.甘肅省軌道交通電氣自動化工程實驗室,蘭州 730070)

隨著國內學者在電氣化鐵道供電領域不斷地研究，同相供電技術也在飛速的發展當中。近年來為解決高速鐵路大容量負荷補償需要、降低有源補償裝置容量，文獻[1]首次提出了基于模塊化多電平換流器(modular multilevel converter，MMC)與組合式接線變流器相結合的有源補償同相牽引供電系統。文獻[2]提出基于MMC的組合式同相供電裝置的拓撲結構和工作原理，并且對其進行了控制策略的研究和仿真分析等。

目前對用于單相組合式同相供電的CPD研究相對成熟的基礎上，其可靠性已成為領域內的熱點關注問題。在同相供電領域已有相關文獻對多種具體結構進行了系統可靠性的分析。文獻[3-4]考慮了大功率電子元器件的物理損傷機理，對同相潮流控制器中的潮流控制器的可靠性以及IGBT(Insulated gate bipolar transistor，IGBT)模塊的可靠性進行了分析。文獻[5]使用貝葉斯網絡和故障樹模型對同相供電牽引變電所的可靠性進行了評估。文獻[6]通過k/n(G)可靠性模型，針對不同結構同相供電裝置分析其可靠性，并選擇適當的可靠性優化方式進行備用情況的優化設計。

上述文獻在同相供電領域從不同角度對不同對象和結構進行了可靠性方面的研究，而涉及到單相組合式同相供電MMC-CPD可靠性的研究并未深入。本文將首先介紹單相組合式同相供電系統以及單相組合式同相供電級聯式CPD和MMC-CPD的詳細拓撲結構。其次對級聯式變流器和MMC以及CPD進行可靠性分析。最后，結合算例對比分析級聯式CPD和MMC-CPD的可靠性并且進行MMC-CPD子模塊冗余配置優化。

1 系統簡介

1.1 組合式同相供電系統

單相組合式同相供電系統在直接供電方式的結構如圖1所示。

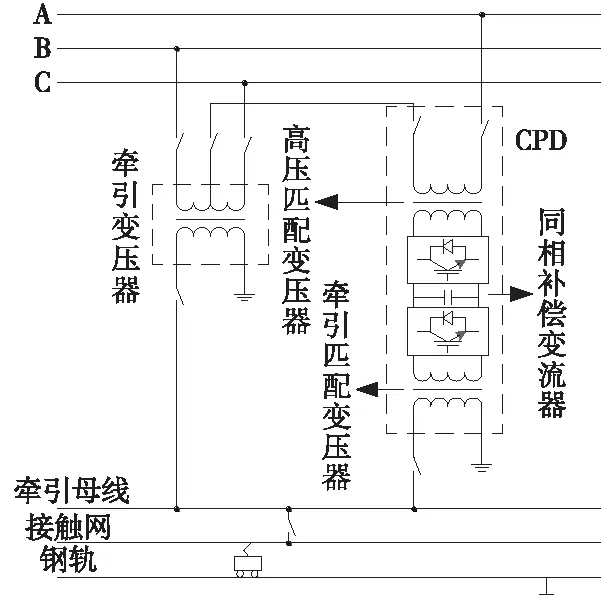
圖1 直供方式單相組合式同相供電系統

單相組合式同相供電系統的牽引變電所包含兩個部分，牽引變壓器以及同相供電裝置CPD。CPD由高壓匹配變壓器，同相補償變流器，交流電抗器和牽引匹配變壓器組成。組合式同相供電系統的工作原理是：當牽引負荷功率小于等于同相補償變流器額定容量的2倍時，牽引變壓器和同相供電裝置各承擔牽引負荷功率的一半，此時負序電流得以全部補償，三相電壓不平衡度為0；當牽引負荷功率大于同相補償變流器額定容量的2倍時，同相供電系統按照同相補償變流器的額定容量供給，牽引變壓器承擔剩余牽引負荷功率，此時，負序電流未得到全部補償，但它引起的三相電壓不平衡度滿足我國電能質量要求[7]。

1.2 單相組合式同相供電MMC-CPD拓撲結構

單相組合式同相供電MMC-CPD拓撲結構如圖2所示[8]，其中牽引側和負載側分別有高壓匹配變壓器HMT和牽引匹配變壓器TMT。同相補償變流器MMC包括兩個橋臂，每一個橋臂有上下兩個半橋臂，各包含N個子模塊SM。Lc是橋臂緩沖電感。

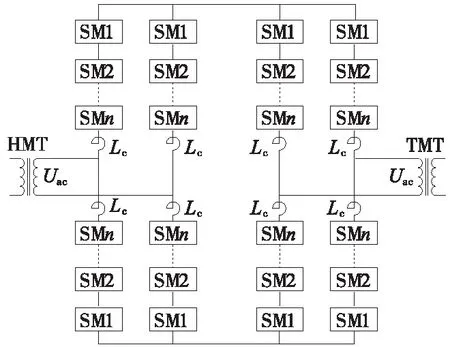
圖2 單相MMC-CPD拓撲

值得一提的是MMC的子模塊結構選擇有很多，比如全橋子模塊、半橋子模塊或者混合結構子模塊。采用全橋子模塊或混合結構子模塊的MMC具有相應的故障穿越能力，然而隨著元器件數量的增多，其損耗與成本也會隨之提高。故采用了經濟性相對較高的單相半橋子模塊[9]，結構如圖3所示。

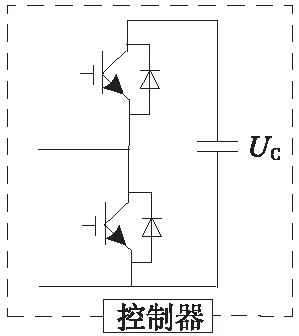
圖3 半橋子模塊

1.3 單相組合式同相供電級聯式CPD拓撲結構

級聯式CPD是由多個相同的功率模塊級聯，從而滿足實際工程需求。其中每一個功率模塊都是BTB(Back to Back，BTB)式的交直交變流器，如圖4所示。

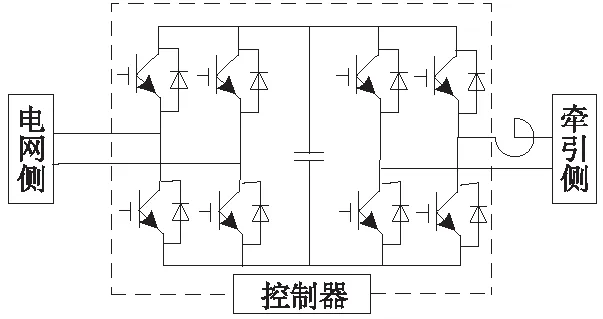
圖4 功率模塊

單相級聯式CPD的拓撲結構如圖5所示，其中L為連接電感。

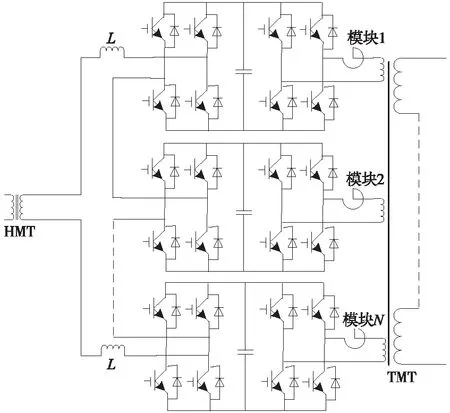
圖5 單相級聯式CPD拓撲

2 CPD可靠性模型

CPD包括高壓匹配變壓器和牽引匹配變壓器以及變流器，將分別討論級聯式變流器和MMC的可靠性。

2.1 k/n(G)系統可靠性模型

假定目標系統是由n個相互獨立且具有相同壽命分布的元件組成，k/n(G)系統也稱作n中取k的冗余表決系統，是指當n個元件中至少有k個元件正常工作時，系統正常工作，即失效的元件數≤n-k，反之則系統失效。設每個元件的不可靠度為q，可靠度為p，顯然元件只有2種狀態，即p+q=1，所以k/n(G)系統的可靠度為[4，10]

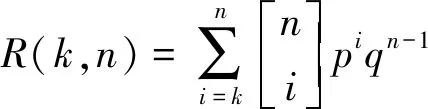
(1)

在元件的壽命服從指數分布的條件下，設故障率為常數λ，則系統的可靠度為

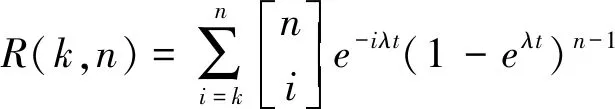
(2)

2.2 元件可靠性

元件可靠性分析的影響因素在于其運行條件，如電壓、電流、濕度、結溫和環境溫度等多種應力。而考慮元件的各種影響因素的物理失效模型結合系統可靠性的分析相對較為困難，如今的研究是建立在不同型號元件在實驗中產生數據的擬合。圖6所示為元件運行的壽命曲線[11]，本文主要研究穩定運行期的可靠性。

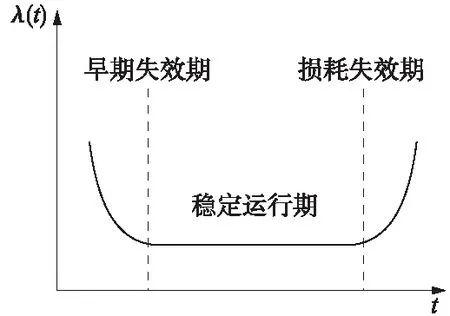
圖6 浴盆曲線

此時，各個元件的可靠度R(t)均服從指數分布[12]

R(t)=e-λt

(3)

其中，λ為元件故障率；t為時刻。

2.3 級聯式變流器可靠性模型

級聯式變流器由相同的數個功率單元級聯而成。根據某段同相供電線路實際工程設計情況，在必要的功率模塊數量之上增加了單元功率模塊，其中每一個功率模塊是相同的(圖4)。故可采用k/n(G)可靠性模型對其進行分析。當變流器正常運行時，需要單個功率模塊中每一個元件都能正常運行，功率模塊可靠度R1(t)由公式(3)可得

R1(t)=[RIGBT(t)]8·Rc(t)·Rsc(t)·RL(t)

(4)

其中，RIGBT(t)為IGBT模塊可靠度，Rc(t)為子模塊電容可靠度，Rsc(t)為控制器可靠度，RL(t)為串聯電抗器可靠度。

由圖5可知，級聯式變流器是由兩個連接電容以及數個相同功率模塊組成。利用k/n(G)可靠性模型對級聯式變流器進行可靠性建模可得

RJL(t)=[RL(t)]2·

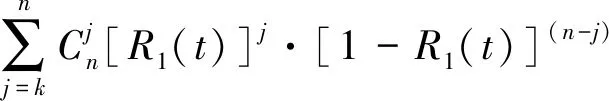
(5)

2.4 MMC可靠性模型

MMC分為整流和逆變兩部分，其分別由相同結構單相橋臂構成。各橋臂包含一定個數的子模塊和一個橋臂緩沖電感。在此之外，變流器的正常運行與控制系統和冷卻系統也是密不可分的[8]，控制系統包括觸摸屏、PLC、輔助供電系統和主控板。冷卻系統包括內冷系統、外冷系統和監控系統。根據其運行原理控制系統和冷卻系統可視為串聯模型。

MMC在正常運行中任意各子系統故障都會導致系統無法正常運行，橋臂結構組合關系和MMC結構組合關系分別如圖7、圖8所示。

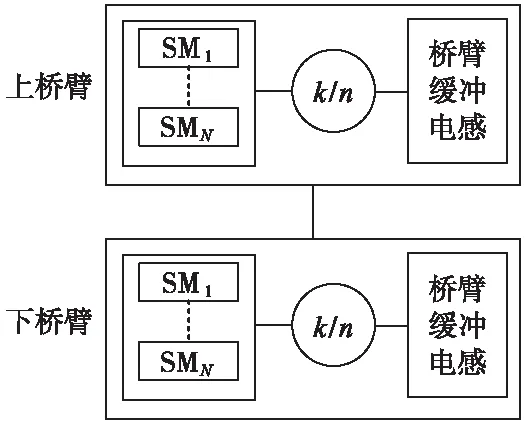
圖7 橋臂結構組合關系

圖8 MMC結構組合關系

2.4.1 MMC子模塊可靠性模型

采用單相半橋子模塊(圖3)。各個橋臂里的單相半橋子模塊均為兩個IGBT模塊和單個子模塊電容以及控制器構成，其可靠性由它們共同決定，任意元器件損壞則無法正常運行。

半橋子模塊在t時刻可靠度RSM(t)的計算如下

RSM(t)=RIGBT1(t)·RIGBT2(t)·Rc(t)·Rsc(t)

(6)

其中，RIGBT1(t)和RIGBT2(t)為IGBT模塊可靠度，由于其結構相同，取值亦相同。

2.4.2 MMC可靠性模型

由上文可知每條橋臂是通過上下兩部分子模塊以及橋臂緩沖電感串聯而成。可得上、下橋臂可靠度Rarm(t)均為

Rarm(t)=[RSM(t)]k×RL(t)

(7)

其中，RSM(t)為子模塊可靠度，RL(t)為緩沖電感可靠度，可根據失效率代入公式(3)計算，k為不考慮容錯措施下每條橋臂必要子模塊數量。

在同相供電裝置實際運行中，安全穩定的運行是極為重要的，一般考慮通過增加冗余設計以提高系統運行的可靠性。冗余設計分為冷備用和熱備用兩種模式，本文主要討論熱備用策略下橋臂的可靠性。

熱備用策略指在變流器正常運行狀態下，使備用子模塊和原有必要子模塊同時工作，當某時刻出現一定數量子模塊故障時，仍然能確保可工作的子模塊數量≥k，橋臂電壓滿足變流器正常運行要求。在此情況下，橋臂可靠度可利用k/n(G)模型計算，即當有n-k+1個子模塊故障時，橋臂將無法正常運行

[1-RSM(t)](n-j)

(8)

其中，Rarm(t)為熱備用下橋臂可靠度。

由圖2可知，變流器包括4條結構相同的橋臂，其中每條橋臂都包含上橋臂、下橋臂兩部分以及兩個緩沖電感。在此之外，變流器單元還包括冷卻系統和控制系統，控制系統的可靠度函數Rkz(t)和冷卻系統可靠度函數Rcs(t)可表示為

Rkz(t)=Rts(t)·Rplc(t)·Raps(t)·

Rmcp(t)·Rcs(t)

(9)

Rcs(t)=Rin(t)·Rout(t)·Rjk(t)

(10)

式中，Rts(t)、Rplc(t)、Rcs(t)、Raps(t)和Rmcp(t)分別為觸摸屏、PLC、輔助供電系統和主控板的可靠度；Rin(t)、Rout(t)和Rjk(t)分別為內冷系統、外冷系統和監控系統的可靠度，通過式(2)可計算得出。由此MMC可靠度可得

RMMC(t)={[Rarm-h(t)]2}4·Rkz(t)·Rcs(t)

(11)

考慮到同相供電系統的高可靠性需求，控制系統和冷卻系統一旦出現故障也會直接導致整個系統的停運，所以一般可設置1套熱備用系統。如果裝置中一套系統出現故障時，它將即刻停運。而另一套系統將立即變為使用狀態，同樣能保證同相供電系統的正常運行。控制系統和冷卻系統熱備用情況下的可靠度Rkz-h(t)和Rcs-h(t)可表示為

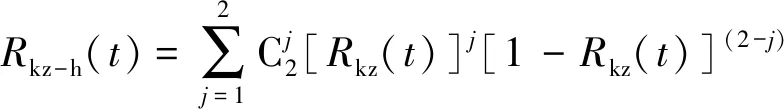
(12)

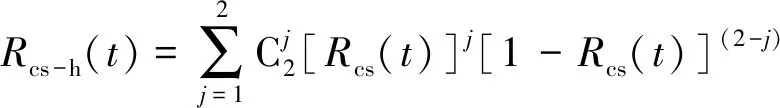
(13)

其中，Rkz(t)和Rcs(t)為上文無備用情況時控制系統和冷卻系統的可靠度。此時MMC的可靠度可表示為

RMMC-h(t)={[Rarm-h(t)]2}4·Rkz-h(t)·Rcs-h(t)

(14)

2.5 單相組合式同相供電CPD可靠性模型

單相組合式同相供電CPD是由高壓匹配變壓器和牽引匹配變壓器以及變流器組成的。由于兩個匹配變壓器工程上一般不做冗余設計，視為串聯結構。故，CPD可靠度RCPD(t)可表示為

RCPD(t)=RConverter(t)·RTMT(t)·RHMT(t)

(15)

其中RConverter(t)將分別代入級聯式變流器和MMC的可靠度進行計算。通過CPD可靠度函數RCPD(t)，可以求得系統的平均無故障工作時間TMTTF為[13]

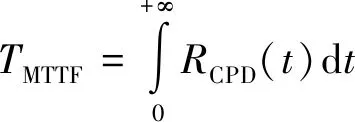
(16)

3 算例分析

3.1 橋臂子模塊數量計算

在考慮容量需求的前提下，決定必要子模塊數量的關鍵因素是功率器件的耐壓、耐流水平，故其數量可通過如下公式計算[2]

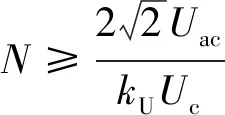
(17)

式中，N為橋臂子模塊數量；Uac為變流器輸入電壓；kU為調制比；Uc為直流支撐電容額定電壓；本文采用額定電壓為1 100 V的直流電容。在實際工程使用當中，應當考慮冗余設計。

3.2 無備用分析

單相組合式同相供電裝置(CPD)結構如圖1所示，高壓匹配變壓器HMT可完成220 kV(110 kV)/27.5 kV(10 kV/6 kV)的電壓變換[7]，綜合考慮輸出電壓的質量以及各子模塊的耐壓水平，本文采用10 kV的輸入電壓。根據公式(17)并選擇調至比0.95的控制方法，可計算得出MMC必要橋臂子模塊數量為28。

用于單相組合式同相供電的MMC-CPD尚未應用于實際工程當中，可靠性統計數據暫時缺失，本文所采用的數據為已經應用于實際工程的組合式同相供電匹配變壓器、級聯式變流器以及MMC的統計數據，并結合工程經驗部分修正，如表1所示。

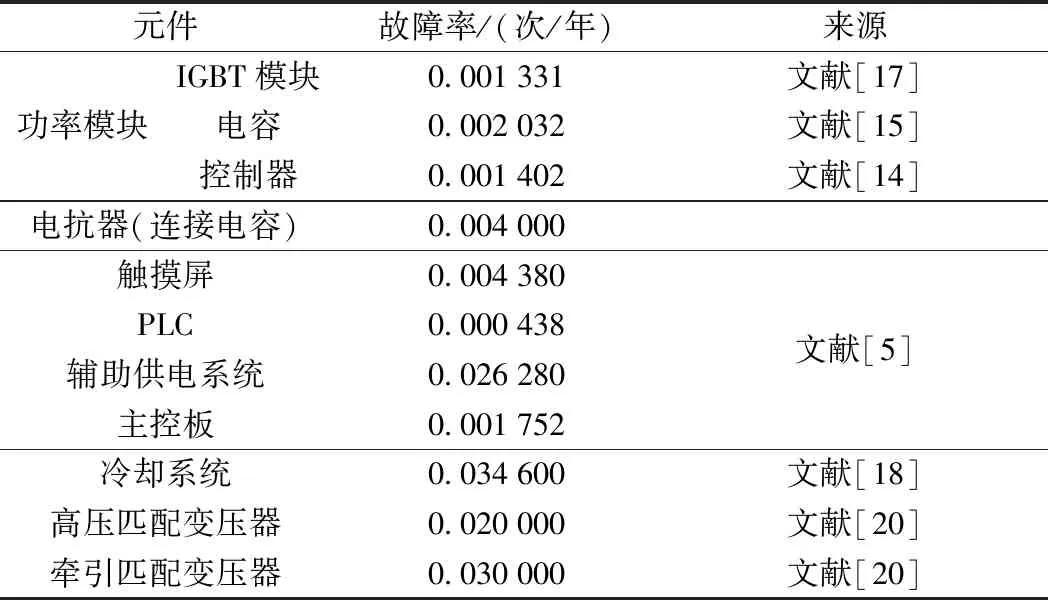
表1 器件失效率

在不考慮備用策略的情況下，CPD均包含1個高壓匹配變壓器、1個牽引匹配變壓器以及分別加入級聯式變壓器和MMC。

根據某段鐵路同相供電運營中的級聯式CPD，其必要功率模塊數量為13個[4]。通過公式(15)和公式(16)可分別計算求得在無備用情況下CPD的可靠度曲線如圖9所示、平均無故障工作時間TMTTF如表2所示。

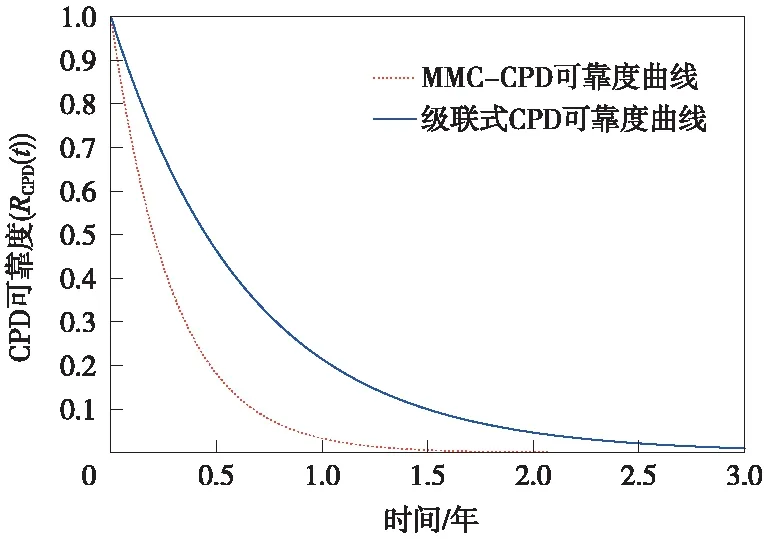
圖9 CPD可靠度曲線

表2 無備用運行CPD TMTTF

由此可以看出，在滿足正常運行需求的情況下，級聯式同相供電裝置的可靠性高于MMC-CPD。

3.3 MMC-CPD冗余分析

由于MMC-CPD在提高有源補償容量、減少開關頻率、減少開關器件應力、降低開關器件損耗、節約場地等方面表現出明顯的優勢，針對子模塊冗余度對可靠度的影響進行了分析。由上文可知滿足同相供電需求的MMC-CPD的單個橋臂必要子模塊數量為28個，以每次2個子模塊的數量增加冗余配置，MMC-CPD的可靠度增量曲線如圖10所示。

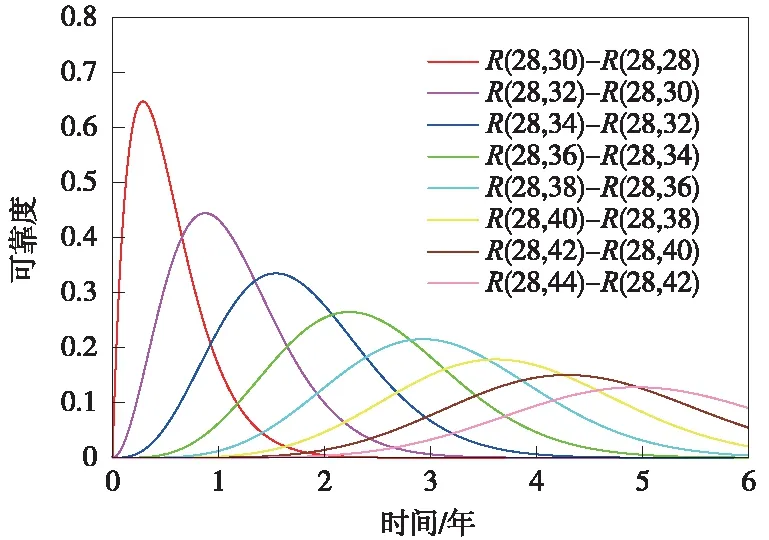
圖10 可靠度增量曲線

k/n(G)系統主要的意義是提升短期的系統可靠性[21]。對MMC-CPD運行1年時的可靠度在不同冗余配置下的表現進行計算，結果如表3所示。

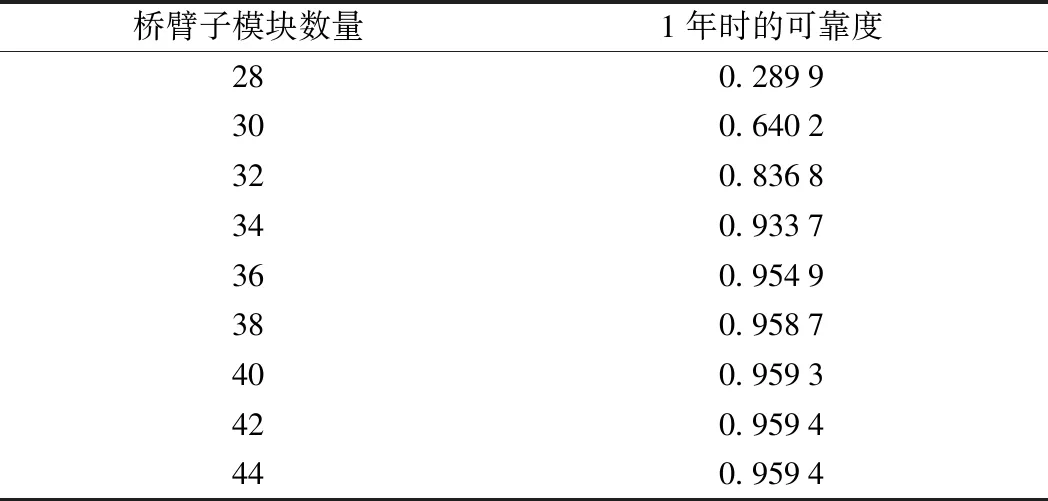
表3 不同冗余配置下MMC-CPD可靠性指標

由表3可以看出，橋臂子模塊對MMC-CPD有明顯的影響，但是隨著冗余度的增加，其貢獻程度呈下降趨勢。可以觀察出在每個橋臂增加8個子模塊之后，運行時間為1年時的可靠度將不再有明顯的提升。

4 結論

本文分別分析了兩種單相組合式同相供電裝置(級聯式CPD、MMC-CPD)的拓撲結構，在此基礎上建立了基于k/n(G)可靠性模型的級聯式CPD和MMC-CPD在熱備用下的可靠性模型。通過可靠性模型對比兩種變流器在滿足同相供電裝置正常運行的必要需求下的可靠性指標。此外，對MMC-CPD的冗余配置進行了探討，得出如下結論。

(1)基于k/n(G)可靠性模型，計算出級聯式CPD和MMC-CPD在正常運行的必要條件下的TMTTF，證實了在此情況下，級聯式CPD的可靠性高于MMC-CPD。

(2)MMC-CPD隨著橋臂子模塊冗余配置的增加，對其可靠性的貢獻顯著。

(3)根據運行1年為基準，對MMC-CPD橋臂子模塊冗余配置和可靠度的關系，優化了冗余配置，為將來MMC-CPD的冗余設計提供了依據。