用于列車定位的RAIM算法改進研究

趙 妍,米根鎖

(蘭州交通大學自動化與電氣工程學院,蘭州 730070)

引言

在實際列車運行過程中，導航系統中存在故障衛星會使可見衛星數目不足或衛星結構分布不良，從而導致車載接收機到衛星之間的偽距值出現偏差，進而計算的列車實際位置結果不準確威脅行車安全[1，2]。因此，針對如何及時檢測識別故障衛星進行研究顯得十分重要。RAIM(Receiver Autonomous Integrity Monitoring，接收機自體完好性監控)算法是接收機內部通過接收機自身多余觀測值，對衛星的多個導航解進行一致性檢驗，從而達到監測列車定位完好性的目的[3-4]，以保證列車的安全運行。

目前，RAIM算法逐步在鐵路領域展開研究。文獻[5]對RAIM算法在鐵路領域的可用性做出判斷，但未對故障衛星的檢測與識別做出研究；文獻[6]提出用傳統RAIM算法計算的檢驗閾值，但直接檢驗的漏警率較大。文獻[7]提出一種基于擴展卡爾曼濾波器的RAIM算法，新算法性能增益無明顯提高，但為后續EKF-RAIM算法的研究奠定了基礎。文獻[8]設計了一種雙遞歸粒子濾波器的RAIM算法用于分離定位和速度估計，但對鐵路領域未進行驗證。文獻[9]提出加權最小二乘法，針對北斗/GPS組合導航系統的電離層、對流層干擾因子進行研究。

針對上述問題，根據我國自主研發的北斗衛星導航系統運用到列車定位中的特殊形式，提出以ATPL(沿股道方向保護級別，Along Track Protect Level)為判據的RAIM算法，同時，在故障衛星識別環節引入加權因子C。以青藏鐵路某路段實際運行數據為例進行仿真驗證，證明改進算法的有效性。

1 北斗導航列車定位原理

北斗衛星導航定位系統通過測量出已知位置的衛星到車載接收機之間的距離(偽距)，綜合多顆可見衛星的數據，根據三曲面相交確定動態點計算車載接收機的位置信息[10-12]。北斗衛星導航系統定位框圖如圖1所示。

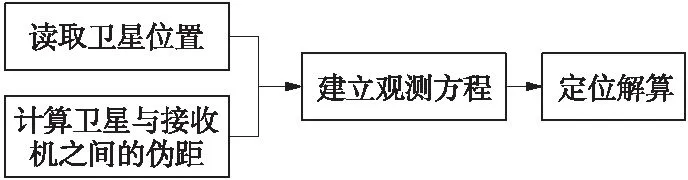
圖1 北斗導航系統定位框圖

2 基于ATPL的RAIM算法

2.1 基于ATPL算法的RAIM可用性判斷

2.1.1 使用參數

(1)可見衛星判斷

在實際工程中，衛星的高度角h>15°(衛星遮蔽角)時，表明該衛星為可見衛星[13]。可見衛星判別如圖2所示。

圖2 可見衛星判別

(2)完好性水平告警限值

文獻[14]指出完好性水平告警限值(HAL，Horizontal Alert Limit)是RAIM算法可用性重要影響因素之一，RAIM算法可用性要求衛星保護級別必須小于告警限值，保護級別越低表明算法使用的可靠性越高。見表1。

表1 不同線路HAL值及可用性

2.1.2 RAIM算法可用性判斷

RAIM算法可用是故障衛星檢測和識別的前提，圖3為RAIM可用性判斷流程。

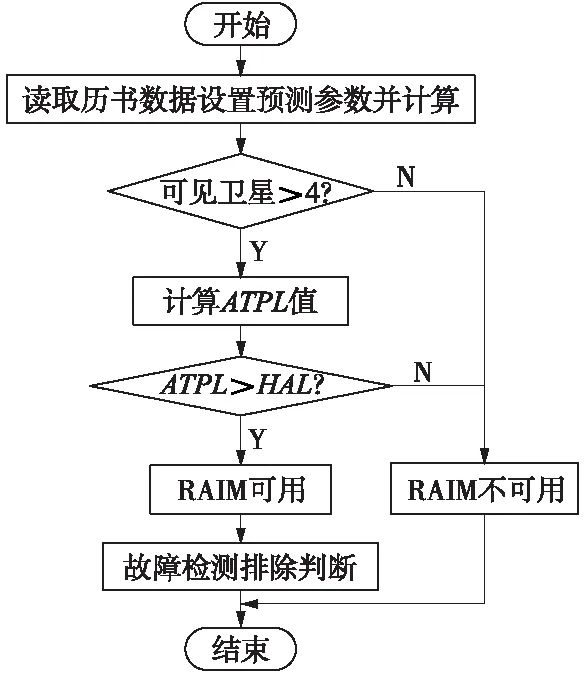
圖3 RAIM可用性判斷流程

在鐵路領域，列車沿固定方向，在固定路線上行駛(一維坐標)，進而直接定義ATPL作為RAIM算法是否可用的判據，在計算ATPL過程中加入列車質心速度方向與鋼軌的夾角(航向角)，對傳統RAIM算法進行改進。

根據讀取的廣播星歷計算得出，當可見衛星數>4時，表明可以進行RAIM算法可用性判斷；當可見衛星數目>5時，表明RAIM算法可以檢測到故障衛星，同時可將故障衛星排除。

ATPL的計算

ATPL=KAT×dAT

(1)

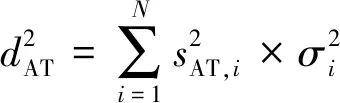
(2)

(3)

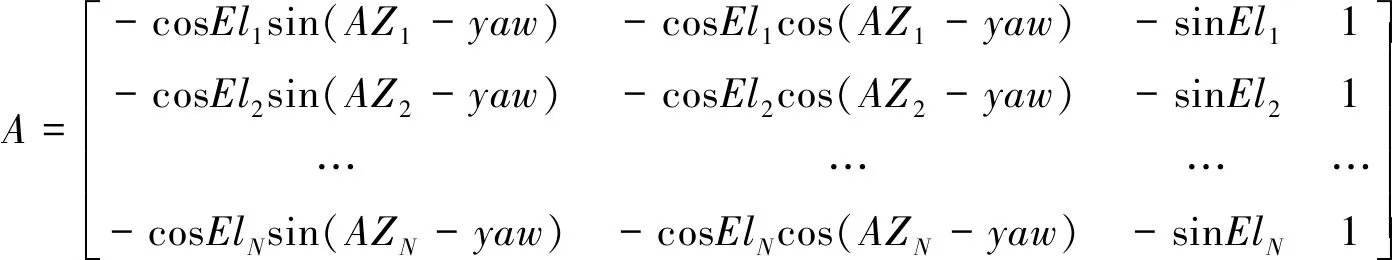
(4)

其中，KAT指一維高斯分布情況下的常數6；σi指第i顆衛星偽距測量誤差的標準差；H為加入導航角后的N×4的觀測陣；yaw指東北天坐標系下列車航向角；AZi指每個衛星方位角；Eli指每個衛星高度角。

將計算的ATPL與HAL進行比較，判斷RAIM算法是否適用。當ATPL>HAL時，說明RAIM算法可用，可進行下一步故障衛星的檢測與識別。

2.2 最小二乘殘差法故障衛星檢測識別

2.2.1 使用參數

(1)故障檢測參數

RAIM的技術性能由系統的完好性參數決定，航空無線電委員會(RACA，Radio Technical Commission for Aeronautics)指出完好性參數有漏警率PMD、誤警率PFA、告警時間TTA[15-18]。

PMD是指已出現故障衛星，而RAIM技術沒有檢測出故障衛星的概率。

PFA是全球衛星導航系統(GNSS，Global Navigation Satellite System)在未超出所設定限制的情況下，采用RAIM算法進行檢測發出告警的概率。北斗衛星導航系統的最大誤警率為0.333×10-6。

TTA是指從發現衛星故障到做出報警的時間間隔。一般導航系統告警時間為6 s。

(2)位置精度因子

位置精度因子(PDOP，Position Dilution of Precision)是可以反映用戶所在位置誤差與衛星所在位置誤差關系，且準確度較高的定位結果計算的PDOP值越小[19]。

(3)故障衛星分類

接收機自主完好性檢測的故障模式主要包括以下3種。

①衛星信號發播異常，如信號失鎖，信噪比降低。

②故障衛星被提前告知為“不健康”衛星，這主要由導航電文提供。

③發生軟故障導致偽距產生偏差。

2.2.2 最小二乘殘差法故障衛星檢測

當可見衛星數大于5個時，采用RAIM算法對故障衛星進行檢測和識別，圖4為RAIM算法故障衛星檢測與識別流程。

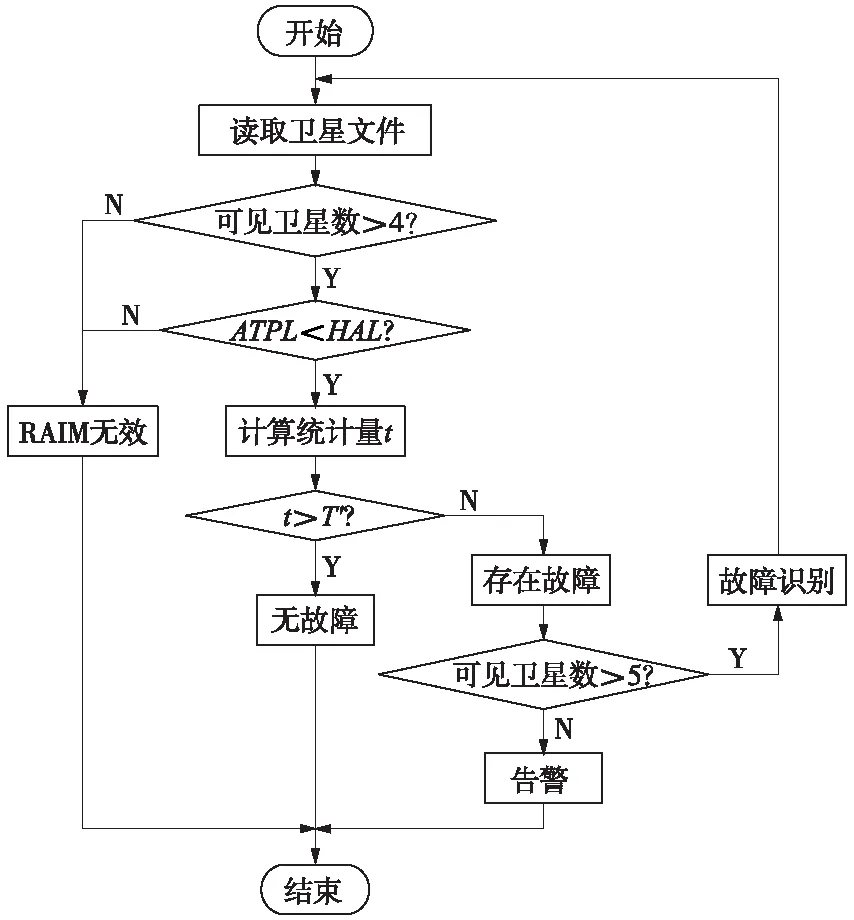
圖4 故障衛星檢測識別流程

(1)北斗衛星導航系統觀測模型

根據北斗衛星導航系統檢測原理，線性化后的在東北天坐標下的接收機偽距觀測方程為

y=Ax+ε

(5)

其中，y指偽距觀測和近似計算偽距差分向量，維數n，y∈RN，N指可見衛星數；A為由衛星到接收機的方向余弦構成的觀測矩陣，A∈RN×4；ε指測量誤差向量，ε∈RN，ε的每個元素分量在衛星無故障時是均值為零的高斯白噪聲。

由最小二乘法可得x的最小二乘估值

(6)

偽距殘差向量

(I-A(ATA)-1AT)(Ax+ε)=

(I-A(ATA)-1AT)ε

(7)

令Q=I-A(ATA)-1AT則(3)式可化簡為

v=Qε

(8)

基于殘差平方和的故障檢測

SSE=vTv

(9)

式中，SSE指衛星偽距殘差向量平方和。

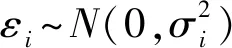
H0(無故障)：E(ε)=0，則SSE/σ2～χ2(n-4)；H1(有故障)：E(ε)≠0，則SSE/σ2～χ2(n-4，λ)。

PFA(誤警率)計算公式

(10)

已知PMD(漏警率)的情況下，當存在故障衛星時，且SSE/σ2～χ2(n-4，λ)，λ的計算公式

(11)

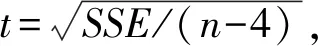
當可見衛星結構分布不良時，故障衛星會對列車定位結果產生較大的誤差，同時，會產生漏檢率。而通過上述算法計算出的t，會有較大漏警發生，為保證RAIM算法在檢測故障衛星時漏檢率的要求，對檢測閾值引入加權因子C，則有T′=CT，0T′時，說明有故障衛星存在。

2.2.3 基于殘差元素的故障衛星識別

當檢測到存在故障衛星后，通過最小殘差二乘法和極大似然估計法進行故障衛星的識別。當被測噪聲滿足正態分布且期望值為零時，用公式(12)識別故障

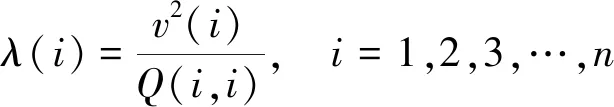
(12)

式中：v(i)指第i號衛星的偽距殘差向量；Q(i，i)指Q矩陣第i行第i列元素。

利用公式(12)計算出每顆衛星的λ值，其中故障衛星的λ值最大。

PDOP值的計算

H=(ATA)-1

(13)

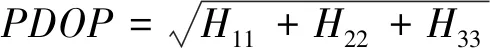
(14)

式中，Hii指H矩陣第i行第i列元素。

3 仿真驗證

3.1 RAIM算法可用性驗證

(1)RAIM算法可用性驗證

根據中國衛星導航系統管理辦公室測試評估研究中心數據可知，亞太地區可見衛星數一般為7～14顆。文獻[20]指出青藏鐵路屬于低密度線路，保護級別為50m。

目前常用以HPL(Horizontal Protect Level)法為判據來判斷RAIM算法的可用性，通過改變判據改進RAIM算法。本次驗證選取青藏鐵路同一路段運行軌跡數據，設置檢測時間720 min，對改進前后RAIM算法可用性進行驗證。圖5是在相同運行軌跡情況下改進前后保護級別對應的保護級別曲線，其中HPL值的波動范圍為11.2～22.6 m，ATPL值的波動范圍為6.1～11.6 m，由于ATPL僅為沿股道方向的保護限值，在同一時間點，ATPL值始終小于HPL值，且在低密度線路保護級別閾值內。經過改進，明顯使該路段的保護值降低，也說明RAIM算法可用。

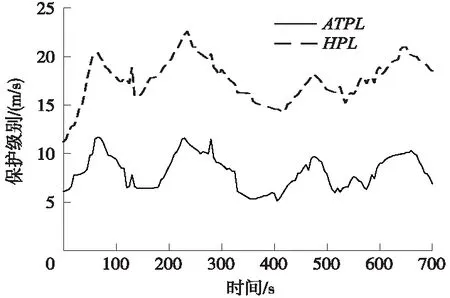
圖5 青藏鐵路某段路線ATPL、HPL曲線對比

(2)加權因子C對RAIM算法的影響

當RAIM算法可用時，根據某型號接收機的誤警率PFA=1/15 000，漏警率PMD=0.001，完好性告警限值HAL=556 m，計算不同C對PFA、PMD及RAIM算法的可用性的影響。見表2。

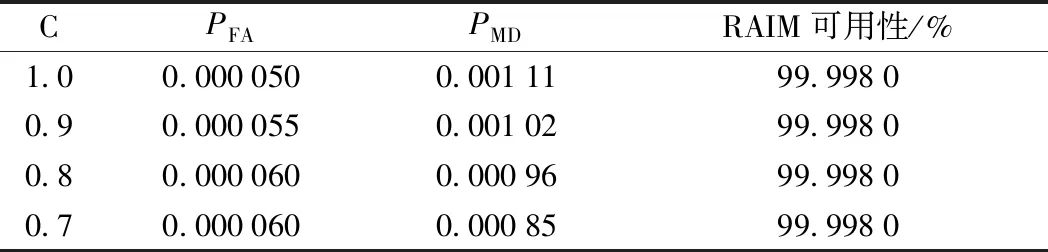
表2 不同C對RAIM可用性及完好性的影響

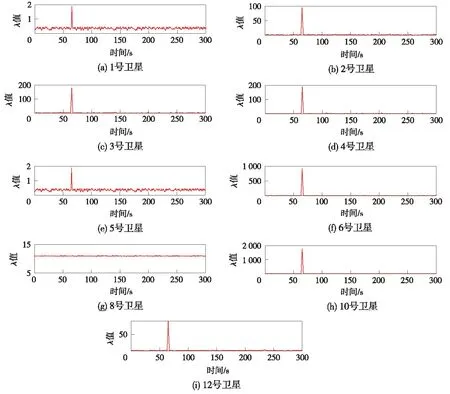
圖7 各衛星λ計算值

根據表2可知，通過引入加權因子C，使PFA及PMD的值有效降低，達到提高RAIM算法可靠性的目的，且在提高可靠性的同時，不影響RAIM算法的有效性。

3.2 RAIM算法故障檢測識別驗證

當RAIM算法可用時，進一步檢測故障衛星和識別故障衛星。由于缺少北斗衛星導航系統在鐵路列車定位應用時的故障數據，因此，結合3.1節數據通過MATLAB仿真軟件對RAIM算法的故障檢測識別功能進行驗證。

本次驗證過程中選取9顆符合列車運行地區的無故障可見衛星，設定檢驗閾值T=4時，設定檢測時間為300 s。對檢測中的10號衛星的第65 s增加90 m的偽距值，制造故障衛星。

對10號衛星增加偽距值后，通過改進的RAIM算法驗證故障衛星是否存在。從圖6可知，檢測過程的第65 s處衛星的檢測量遠大于檢驗閾值T，說明在第65 s處有故障衛星存在。

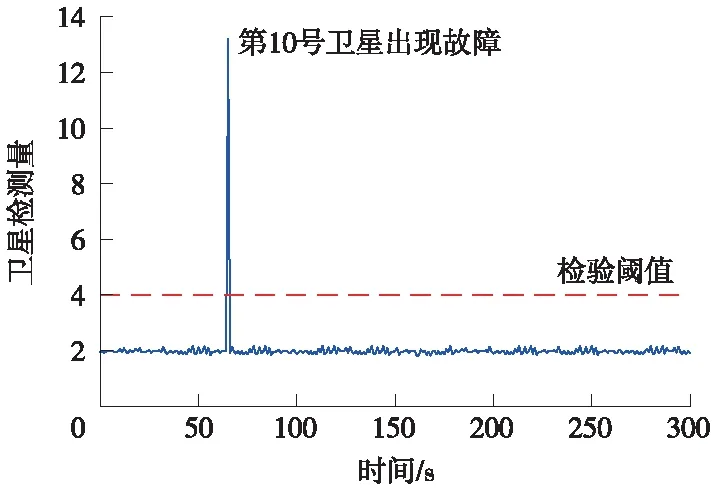
圖6 故障衛星檢測

通過式(12)計算每顆衛星的λ值，曲線如圖7所示圖。根據圖7可得10號衛星的λ值最大，符合制造的故障衛星。因此說明以ATPL為參量的RAIM算法可以識別北斗衛星導航系統中的故障衛星。

通過式(13)式(14)計算得到剔除故障衛星前后的列車運行PDOP曲線(圖8)。根據圖8可得，剔除故障衛星后的PDOP始終小于剔除故障衛星前。通過改進的RAIM算法剔除故障衛星，可以有效降低故障衛星對定位結果PDOP的影響，從而改善衛星故障場景下的定位精度。

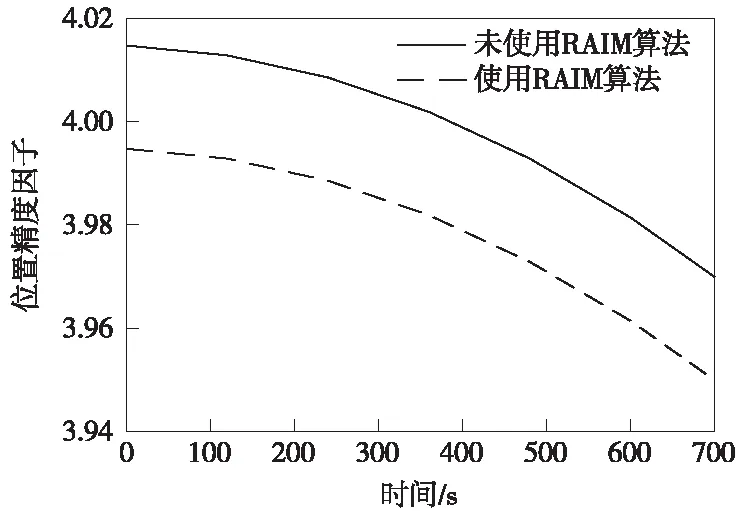
圖8 PDOP變化曲線

5 結論

從提高北斗衛星導航系統列車定位精度和降低漏警率的角度出發，提出了一種改進的RAIM算法。在定位過程中，通過改變RAIM算法判據及檢測閾值，使得保護值及漏警率有效降低，在不影響RAIM算法可用性的同時達到提高可靠性的目的。通過采用青藏鐵路實際列車定位數據進行仿真驗證，結果表明改進的RAIM算法優于傳統RAIM算法，可準確識別故障衛星，降低漏警，減少故障衛星對PDOP影響，能改善列車定位精度，提高北斗衛星用于列車定位的安全可靠性。