內孤立波環境下柱體的受力特性
王 寅,王玲玲,計 勇,席芝橙,張雯雯
(1.南昌工程學院水利與生態工程學院,江西 南昌 330099; 2.河海大學水利水電學院,江蘇 南京 210098)
內波通常發生于密度穩定分層的水體內部[1]。在海洋、河口、湖泊等流體系統中,溫度、鹽度以及其他環境因素引起的密度沿水深方向上的改變,會導致水體密度的分層[2]。在此類環境中,微弱的外界擾動就可能在密度分界面(密度躍層)上引發攜帶巨大能量的內波現象。內孤立波是一種特殊的非線性內波,其振幅大、周期短、所攜能量大[3],大振幅內孤立波對近岸及河口復雜水動力環境中工程結構物的安全穩定性有非常大的影響[4]。內孤立波在傳播過程中以密度躍層為界上下水層呈反向流動,由此產生的剪切流所攜帶的巨大能量會導致異常強大的流速。內孤立波2.1m/s波致流作用下的柱體所承受的最大荷載相當于波長300 m、波高達到18 m的表面波作用[5],這種強烈的作用力可能對近岸及河口復雜水動力環境中水下立管及水下支撐樁柱的安全穩定性造成嚴重的威脅[6]。深入研究內孤立波對水下結構物的作用機理以及結構物內波動力學問題具有非常重要的工程應用價值。
柱體所受水平力可分為壓差阻力和摩擦阻力兩部分[7]。壓差阻力是由于柱體迎流面和背流面的壓差所產生的水平力;摩擦阻力是由于流體黏性作用所產生的水平力,即黏滯力。以往受力研究多只計算出內孤立波對柱體的整體作用力[8-10],并未考慮在不同分層水體中柱體不同部分受力隨水深分布情況,因此并不能獲知柱體詳盡的受力特性。本文借助三維數值波浪水槽,采用大渦模擬(large-eddy simulation,LES)技術模擬內孤立波的產生和傳播,通過提取數模計算結果中不同水層柱體表層的壓強分布及切向速度,采用微元法積分出柱體在各水層所受壓差阻力以及黏滯力,由此獲取受力沿水深分布特性,以揭示分層流環境下柱體的受力機理。
1 控制方程及求解方法
1.1 動量輸運方程
基于連續性假設,可用Navier-Stokes方程(N-S方程)描述不可壓縮黏性流體三維瞬態運動過程:
(1)
(i,j=1,2,3)
(2)
式中:ρ為密度項;t為時間;xi、xj為笛卡爾坐標系的3個方向坐標;ui、uj為笛卡爾坐標系中的3個流速分量;p為壓力項;μ為動力黏性系數;fi為i方向的單位體積力。
1.2 標量輸運方程
采用考慮了兩層水體之間的質量交換作用以及對流-擴散影響的標量輸運方程:
(3)
ρ=C+ρ0
(4)
式中:C為鹽度,kg/m3;k為分子擴散系數;S為源項;ρ0為清水密度,kg/m3。
1.3 大渦模擬
大渦模擬技術是對紊流脈動的一種空間平均,通過濾波函數將大尺度的渦和小尺度的渦分離開[11-14]。過濾后的動量和質量方程可表示為
(5)
(6)
(7)
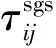
1.4 柱體壓差阻力的求解方法
1.4.1圓柱
如圖1所示,P為水深為y的截面圓柱表面上受到的點壓強(基于數值模擬結果提取),則該截面圓周所受水平方向的壓差阻力fc可定義為
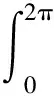
(8)
式中:θ為點壓強P與x軸的夾角,(°),以逆時針為正;l為弧長,cm。

圖1 圓柱壓差阻力計算方法示意圖
基于微元法,可將式(8)離散為
(9)
式中:Pi為作用在第i個微元上的壓力,Pa;θi為第i個微元法線延長線與x軸的夾角,(°),以逆時針為正;n為圓周被等分數,本文取n=360;Δli為第i個微元的弧長,Δli=2πr/n=0.087 cm(r為圓柱半徑,本文取r=5 cm)。
1.4.2方柱
如圖2所示,假定水深為y的截面方柱表面上受到的點壓強為P,則該方柱截面所受水平壓差阻力fs定義為
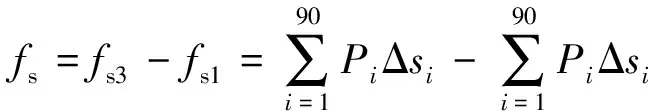
(10)
式中:fsj為作用在方柱截面第j(j=1,2,3,4)條邊上的壓力,N;Pi為方柱各邊第i個微元上的壓力,N;Δsi為第i個微元的邊長,Δsi=4s/m=0.11 cm(s為方柱周長,本文取s=10 cm;m為方柱周長被等分數,本文取m=360)。
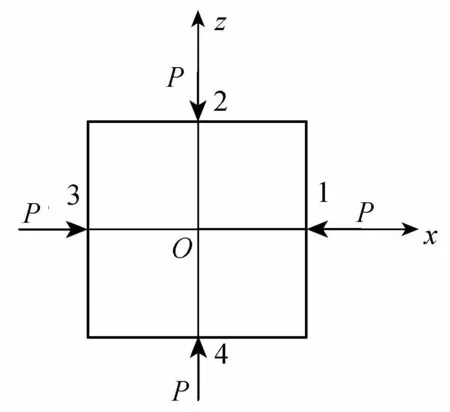
圖2 方柱壓差阻力的計算方法示意圖
1.5 柱體黏滯力的求解方法
1.5.1圓柱
如圖3所示,可將距離圓柱表面最近一層網格上某微元a的切向速度uτ和徑向速度uγ(基于數值模擬結果提取)定義為
uτ=uzcosθ-uxsinθ
(11)
uγ=uzsinθ+uxcosθ
(12)
式中:ux、uz分別為該微元的x方向和z方向速度,cm/s;θ為微元a與x軸的夾角,(°),以逆時針為正。則某微元i所受水平方向上的黏滯力Δfcτi為
(13)
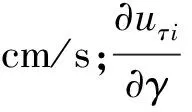
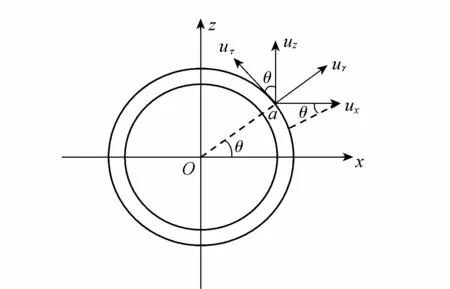
圖3 圓柱黏滯力計算方法示意圖
基于微元法,圓柱表面所受水平方向上的黏滯力fcτ為
(14)
1.5.2方柱
如圖4所示,沿用上述圓柱黏滯力的計算方法,可求得水深為y的截面方柱表面所受水平方向上的黏滯力fsτ:
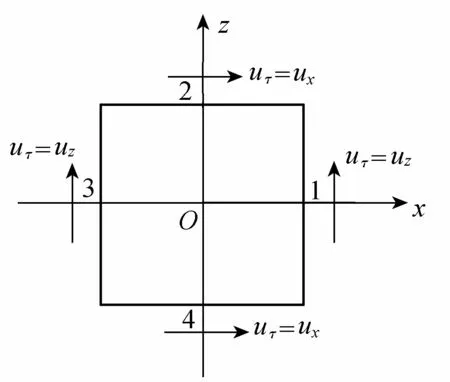
圖4 方柱黏滯力計算方法示意圖
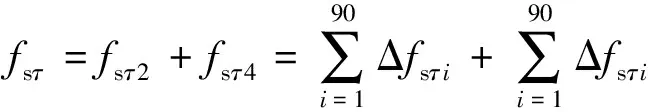
(15)
其中
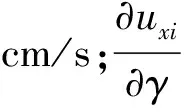
2 數學模型
建立三維數值波浪水槽如圖5所示,水槽長12 m、寬0.6 m、高0.8 m,柱體周圍水平網格和水槽垂向網格劃分方法如圖6、圖7所示。
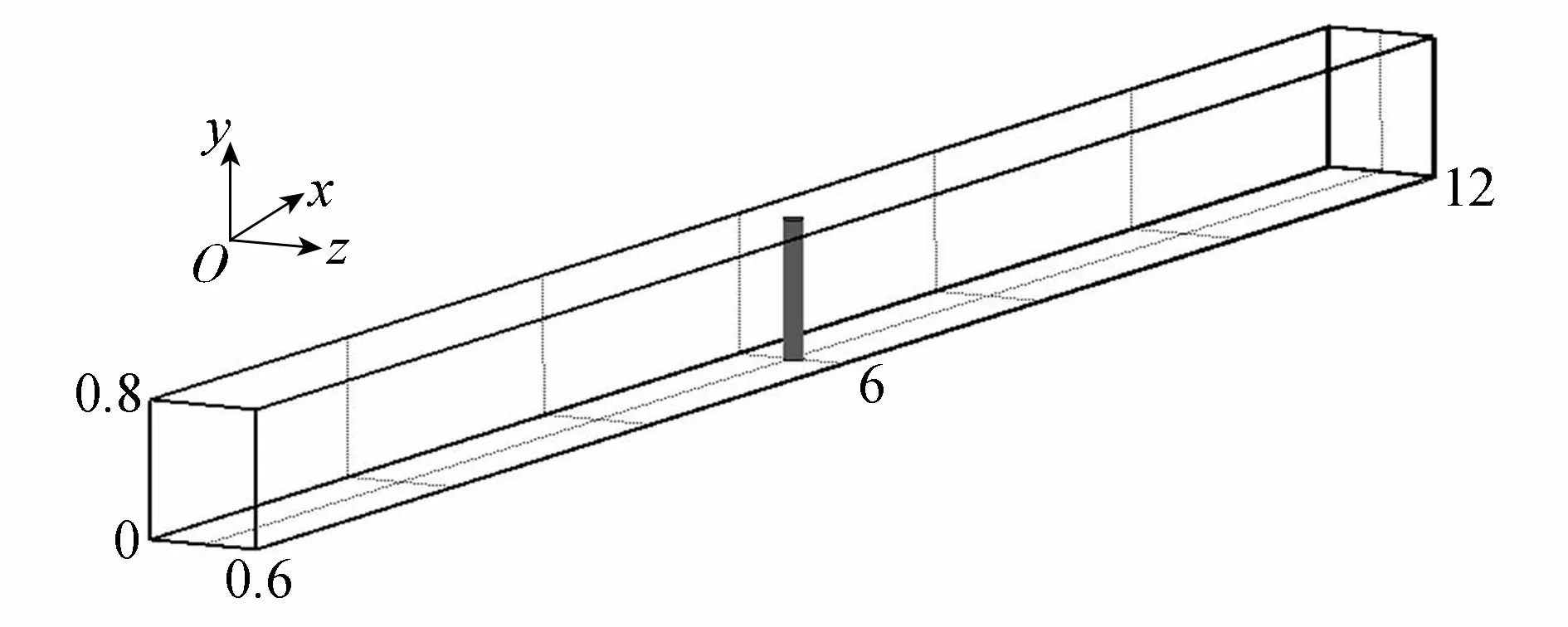
圖5 三維數值波浪水槽示意圖(單位:m)
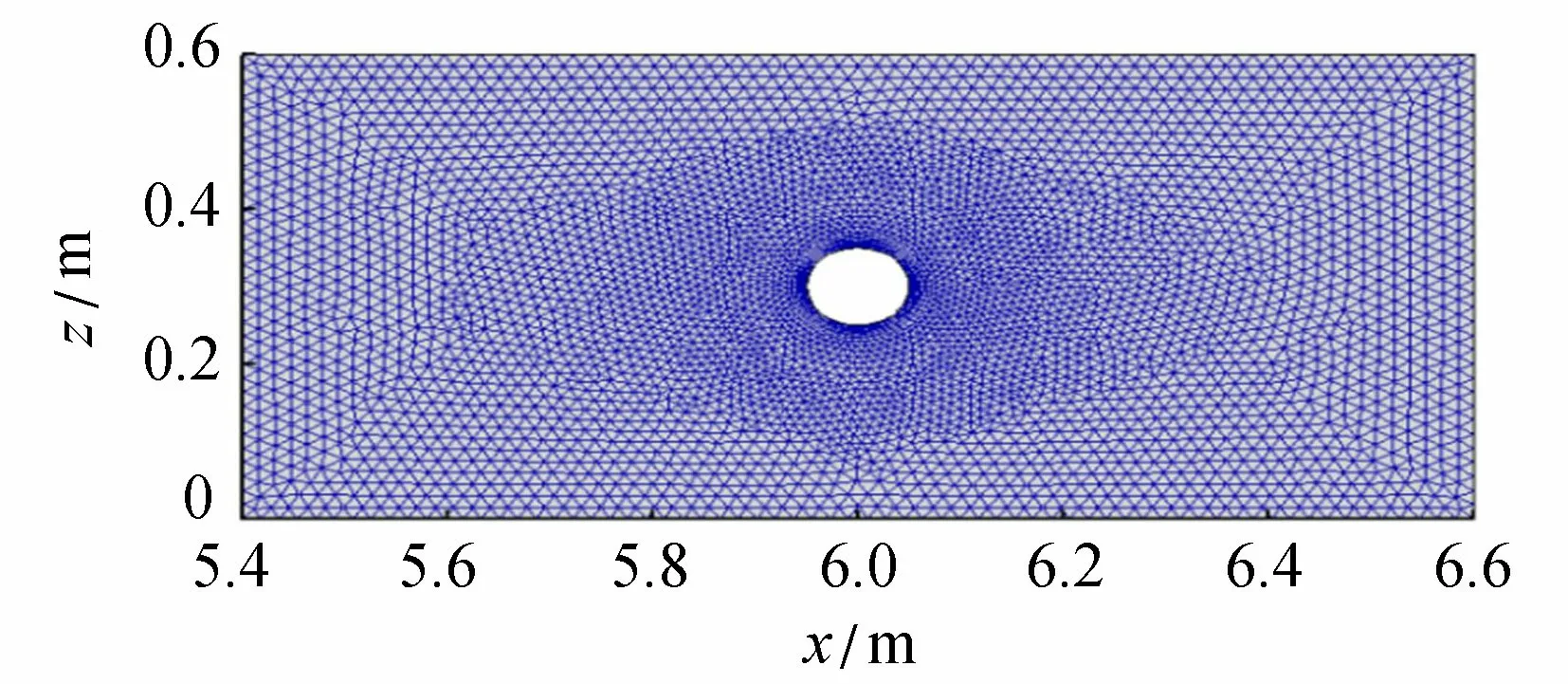
圖6 柱體周圍水平網格劃分方法
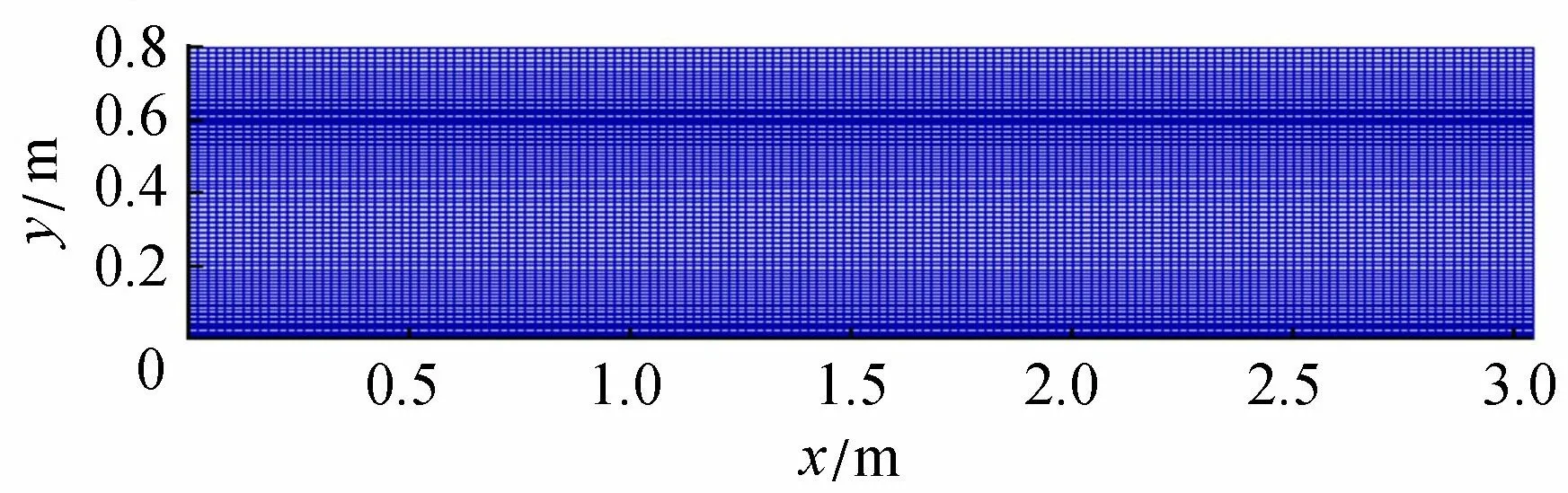
圖7 垂向網格劃分方法
定義在數值模擬中柱體所受的無量綱水平合力F′的計算公式[15]為
(16)
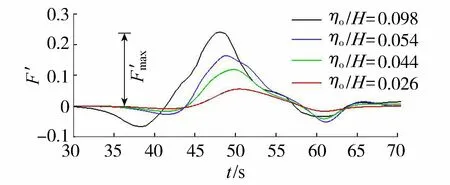
圖8 不同波幅時柱體的F′隨時間t的變化過程
式中:F為數值模擬中計算所得的柱體所受水平力合力,N;A為柱體的迎風面積,cm2;H為水槽總水深,cm;g為重力加速度,m/s2。
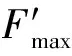
2.1 計算工況
數值模擬采用的波形為下凹型,參數設定及工況選定具體為:上層為清水,密度ρ1=0.998 g/cm3,水層厚度h1=0.2 m;下層為鹽水,密度ρ2=1.017 g/cm3,水層厚度h2=0.6 m,總水深H=0.8 m,設定4種工況N1、N2、N3、N4,相對波幅ηo/H分別為0.026、0.044、0.054和0.098。如圖9所示,采用重力塌陷法制造內孤立波[16],圖中造波區兩側密度躍層高度差ho稱為階躍高度,造波區長度Lo稱為階躍長度。
圖9 重力塌陷法造波示意圖
2.2 數值模擬方法和邊界條件
三維數值波浪水槽中下凹型內孤立波的形成和傳播采用大渦模擬技術模擬;利用SIMPLE算法對流速-壓力項進行耦合,以保證質量守恒,并由此得到壓力場;利用二階中心差分格式及隱式格式分別對空間和時間進行離散。造波區端邊(圖9中的左邊壁)、數值水槽底部以及柱體壁面均采用無滑移固壁邊界,水槽兩側采用滑移固壁邊界。為了使內波不發生反射,水槽右端采用Sommerfeld輻射型邊界[17];頂部采用“剛蓋”假定,以此忽略表面波的影響[17]。
2.3 數學模型驗證
采用與文獻[18-19]相同的方法驗證了建立的數學模型,比較了不同波幅情況下,圓柱和方柱模型試驗與數值模擬中內孤立波作用力的時歷曲線。結果表明模型試驗與數值模擬結果吻合較好,驗證了建立的數學模型的可靠性,可用于后續試驗的模擬。
3 模擬結果與分析
內孤立波環境下的速度場和壓力場與密度均一流環境區別較大,在內孤立波作用下柱體受力三維特性更加明顯[18]。準確剖析柱周流場及柱表壓強分布是科學研究和預測近岸及河口地區樁柱受力的必要條件。柱體所受水平力可分為壓差阻力和摩擦阻力(黏滯力)兩部分,這兩類力求解的基本思路:①在柱身沿垂直(y)方向每隔一定距離截取1個斷面,基于模擬結果在每個斷面上沿柱周向選取360個點,并提取這些點的壓強值及流速值(得到柱周的壓強分布及流速分布);②采用微元法,通過積分不同斷面柱周的壓強分布和流速分布可分別得到圓柱及方柱的壓差阻力f(式(9)(10))和黏滯力fτ(式(14)(15))。
3.1 柱體壓差阻力沿水深的分布
定義柱體在水深y處所受無量綱水平壓差阻力f′為
(17)
3.2 柱體黏滯力沿水深的分布
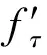
(18)

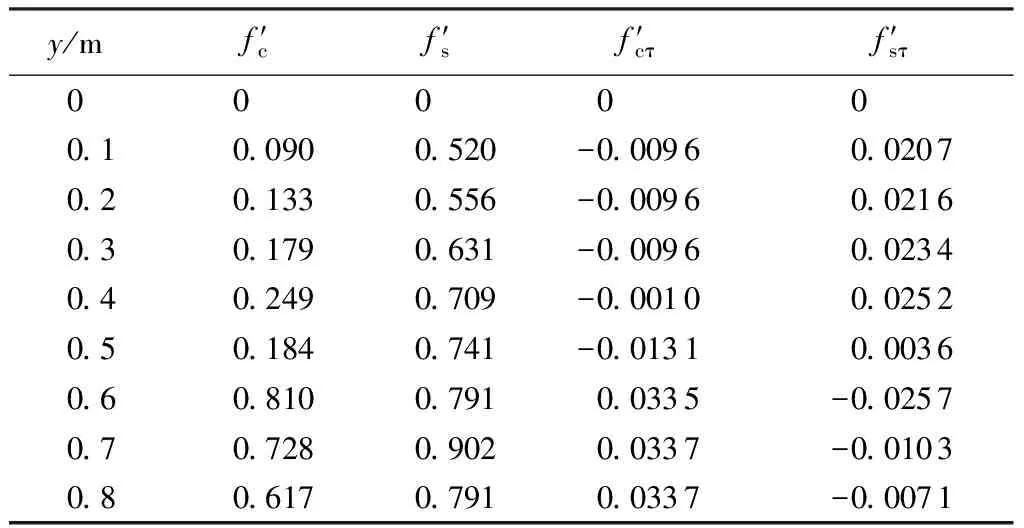
表1 圓柱和方柱的無量綱化水平壓差阻力
3.3 單柱受力的量化分析
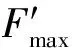
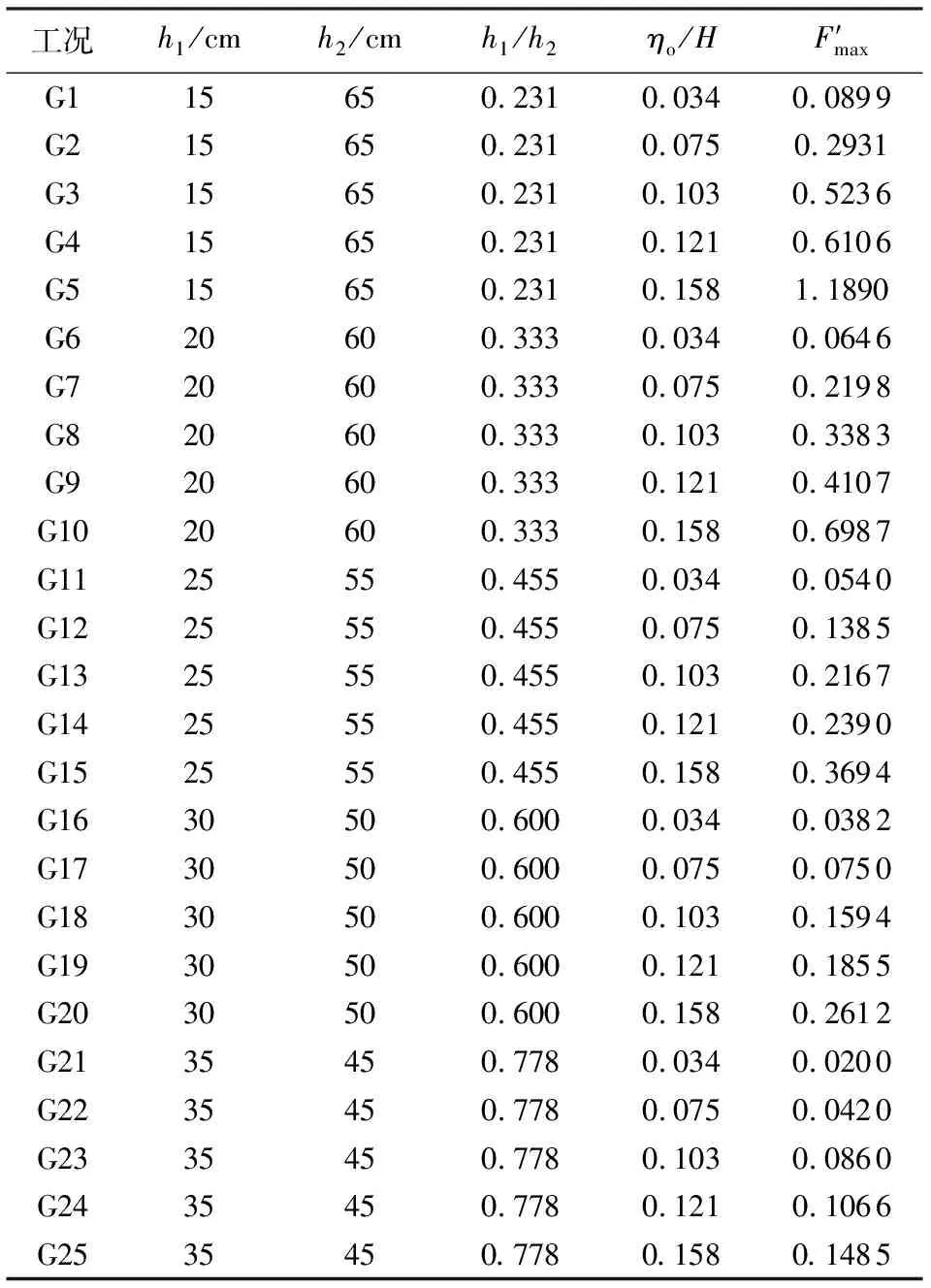
表2 柱體受力量化分析工況設置及相關參數
(19)
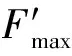
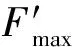
m=-0.88h1/h2+3.72η0/H+0.34
(20)
(21)
此時R2=0.957,擬合優度高(圖10)。綜合影響系數m雖是擬合過程中得到的,但其具有一定的物理意義:內孤立波相對波幅越大、上下水層厚度差距越大,則m值越大,對應柱體受力越大。m為兩參數η0/H和h1/h2對柱體受力的影響提供了量化的指標,且m與η0/H正相關,與h1/h2負相關(式(20))。綜上可知,柱體受力在不同分層條件下均隨相對波幅η0/H的增大而增大;而在同一波幅條件下,水深比h1/h2越大,柱體受力越小。
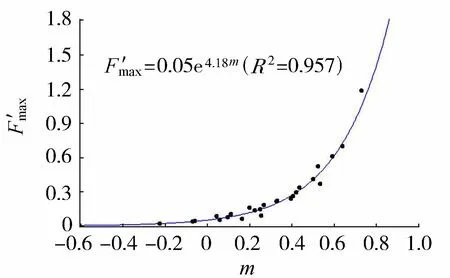
圖與ηo/H和h1/h2的相關關系
4 結 論
a. 波幅相同時,以密度躍層為界,方柱于上下水層中所受到的壓差阻力均大于圓柱:上層水體中方柱受力約為圓柱的1.5倍;下層水體中方柱受力約為圓柱的3.5倍。
b. 作用于柱體上的黏滯力比壓差阻力小1或2個數量級,因此可忽略流體的黏性效應,只考慮壓差阻力的作用效果。
c. 受力峰值系數與相對波幅及水深比具有較強的相關性,且與綜合影響參數呈明顯的指數分布關系,兩者擬合優度為0.957,擬合優度高。受力峰值系數與相對波幅正相關,與水深比負相關。

