運營期上硬下軟型雙層地基動力損傷評價
曹海瑩,杜 量,徐 珊
(1. 燕山大學 建筑工程與力學學院,河北 秦皇島 066004;2. 燕山大學 河北省土木工程綠色建造與智能運維重點實驗室,河北 秦皇島 066004)
0 引言
由于水分蒸發、鹽分沉積和地下水位變幅等原因,在我國沿海和平原地區廣泛分布著一層硬度較大的土層,稱之為硬殼層。由于上硬下軟型雙層地基(簡稱雙層地基)存在具有一定承載能力的硬殼層,一直備受國內外學者的關注[1-2]。文獻[3]詳細闡述了路基中硬殼層的工程特性,并展望了天然硬殼層的利用前景。利用天然硬殼層作為路基持力層,可以節省地基處理的費用,利于優化工程設計。為了降低硬殼層承擔荷載的風險,往往采用低路堤設計方案,這導致了車輛荷載作用下傳遞至路基土動應力的增加,加大了路基運營期失穩的風險性。因此,運營期雙層地基動力特性與工程設計方面仍有諸多問題亟待解決。由于土體動力學性質的復雜性和車輛荷載的隨機性等因素制約[4],相關研究鮮有報道。
目前,關于車輛荷載作用下路基土動力學特性的研究正處于活躍期,許多學者的努力正在使該領域的成果不斷完善和發展。文獻[5-6]開展路基土動應力現場監測工作,收集了寶貴的實測數據,但是因投入的人力、物力大,數據量還未積累到一定規模。文獻[7-9]分別通過室內動三軸試驗、空心圓柱扭剪儀試驗和掃描電鏡試驗,得到了土體動力特性和微觀演化特征方面的有益結論,由于采集的土樣離散性較大,相關結論尚未達成一致共識。文獻[10]構建了車輛-路面-路基相互作用的動力學模型。文獻[11]基于動力互易定理推導出移動荷載作用下的土體振動解析解。文獻[12] 利用累積孔壓模型展開了交通荷載作用下的地基沉降計算,鑒于理論解具有前提假定,需結合具體工況進行應用。文獻[13]借助數值模擬手段再現了車輛運動過程中的加、卸載過程。文獻[14]計算得到路基土中動應力、動應變的時程變化曲線,而參數大小和模型選擇是困擾計算精度的關鍵因素,其結果仍需結合實際工程進一步驗證。
文獻[15]研究表明,車輛荷載作用于低路堤時,動應力的有效影響深度范圍為2.5~6.0 m,而硬殼層的厚度一般為1.0~5.0 m之間,這說明下臥軟土層也被納入路基土的實際工作區之內,因此,研究運營期雙層地基的受力狀態至少需要考慮硬、軟兩個土層。研究層狀路基傳力特性的代表性方法包括:文獻[16-17]采用彈性層狀體系理論及傳遞矩陣法計算動應力傳遞;文獻[18]應用薄層法分析彈性波在層狀介質中的傳播規律;文獻[19]通過數值積分算法獲得了成層地基動應力的簡化計算方法等,而以上方法并未考慮土層界面處動應力非連續的情況。文獻[20-21]分別借助室內模型試驗和有限差分法曾驗證上硬下軟型土層結構在界面處存在動應力突變現象,因此,已有計算手段并不適用于運營期雙層地基的情況,相關研究工作仍有待現場監測數據的支撐和理論方法的改進。
本研究在前人研究的基礎上,以河北省境內的邢臺-臨西高速公路(以下簡稱邢臨高速)雙層地基為研究對象,基于現場監測數據提出硬、軟土層界面處動應力突變的表征參數;結合室內動三軸試驗結果和非線性疲勞損傷累計模型,構建硬、軟土體關聯性損傷變量和雙層地基動力損傷演化方程;借助數據統計手段,對地基土損傷演化信息進行挖掘,給出運營期雙層地基設計的指標依據。
1 現場監測
1.1 監測方案
邢臨高速公路分兩期建設,一期工程邢臺市至威縣段于2003年7月28日開工建設,二期工程威縣至山東界段于2004年5月28日開工,2005年12月21日兩期同步建成通車。設計標準為:雙向四車道、全封閉、全立交高速公路,全長104.64 km,路基寬26 m,設計行車速度100 km/h。低路堤路段路堤高度約2 m左右,最大路堤高度可達到7~9 m。主要路面結構形式:綜合穩定土底基層、水泥穩定碎石基層、中粒式瀝青混凝土下面層和中面層、細粒式瀝青混凝土上面層。
邢臨高速分布著典型的雙層地基土,硬殼層厚度為1.5~4.1 m,主要分布在K33+550~K39+990和K51+550~K60+455區段。對于天然硬殼層作為路基持力層的路段而言,如果增加路堤高度,路堤可近似作為硬殼層的一部分,對動應力擴散起到關鍵作用。與此同時,路堤荷載的增加勢必會加劇硬殼層的承載負擔,如果降低路堤高度,會導致車輛荷載產生的動應力傳遞到更深的地基土中,進而對道路的運營狀況和受力狀態產生不利影響。經過前期試驗路段的摸索,將K33+550~K39+990和K51+550~K60+455區段采用低路堤方案,路堤高度定為2 m左右。共選擇14個典型監控斷面,采用螺旋鉆孔輔助自制夾具的方法埋置動態土壓力盒(XHZ-4XX型電阻應變式),對硬、軟土層界面處的動應力展開監測。監控斷面如下:K33+650,K38+650,K39+990和K51+650共4個監控斷面和K39+750~K39+950路段(每隔20 m設置1個監控斷面),土體物理力學參數見表1。
儀器布設見圖1,在硬殼層底部和軟土層頂部埋設1#和2#動態土壓力盒。有效監控斷面為12個,監測期為1 a(以運營期伊始為起點),每隔10 d收集1次監測數據。
1.2 監測數據整理
以K39+770斷面為例,對監測數據的處理過程進行說明。該斷面路堤填高為2.1 m,為瀝青混凝土路面,監測起止日期為2007年6月—2008年6月,其動應力監測數據如圖2所示。
圖2中每個土壓力盒的監測數據獲取過程如下:每個斷面的監測間歇時間為10 d,每次采集約40~50組數據(即同類型車輛經過該監測斷面40~50次,每組數據均對應1條動應力波動曲線,取動應力峰值作為該曲線的代表值),然后對各組數據中的動應力峰值取平均作為本次監測的數據點(剔除異常數據)。在獲取樣本時,每次采集數據所針對的車輛荷載類型是相同的,但是同一斷面相鄰次的車輛荷載類型不同,例如:第1次僅監測大型貨車(起始時間),第2次僅監測中型貨車(第10天),第3次僅監測小轎車(第20天)。
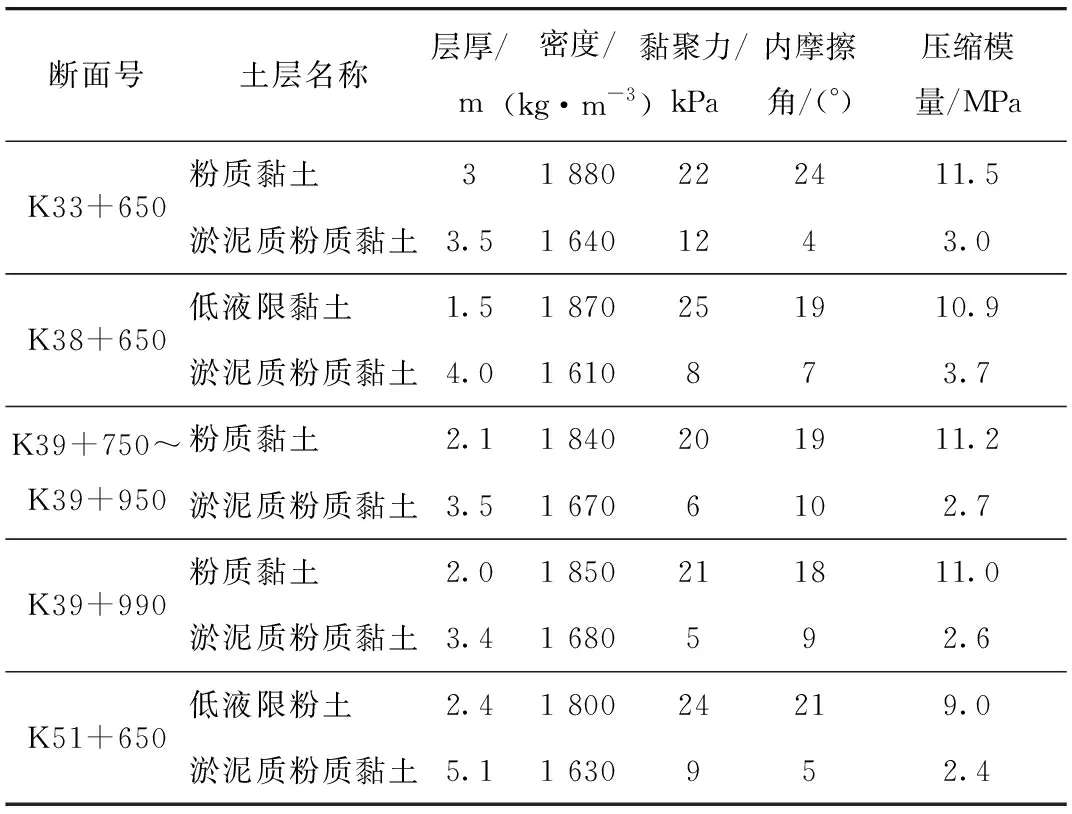
表1 土體物理力學參數Tab.1 Physico-mechanical parameters of soils
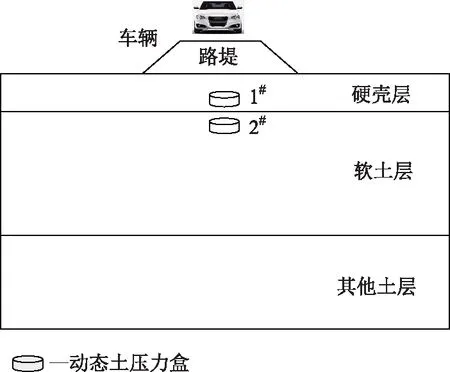
圖1 監測儀器布設Fig.1 Layout of monitoring instrument
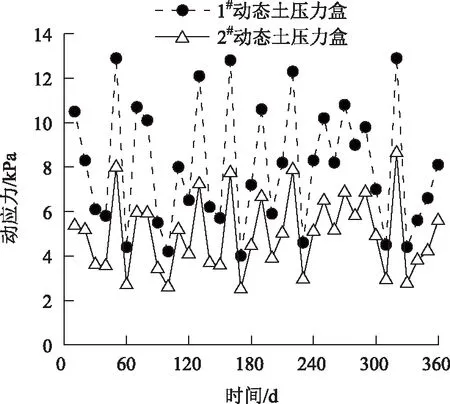
圖2 K39+770斷面動應力監測數據的平均值Fig.2 Average values of dynamic stress monitoring data (section K39+770)
由圖2可知,受到車輛荷載大小、車速變化等多種因素的影響,1#和2#動態土壓力盒的監測數據波動性較大,真實反映了車輛荷載作用下土層中動應力的響應特征,符合統計學中抽樣隨機性的原則。依據文獻[20]室內模型試驗結果驗證和文獻[22]理論計算公式的估算,圖2中的數據具有可靠性。
定義動應力界面傳遞系數為ξ,即:
(1)
式中,σd1為硬殼層底部的動應力幅值(1#動態土壓力盒;σd2為下臥軟土層頂部的動應力幅值(2#動態土壓力盒)。
利用式(1)對圖2中的原始數據進行處理,計算結果如圖3所示。
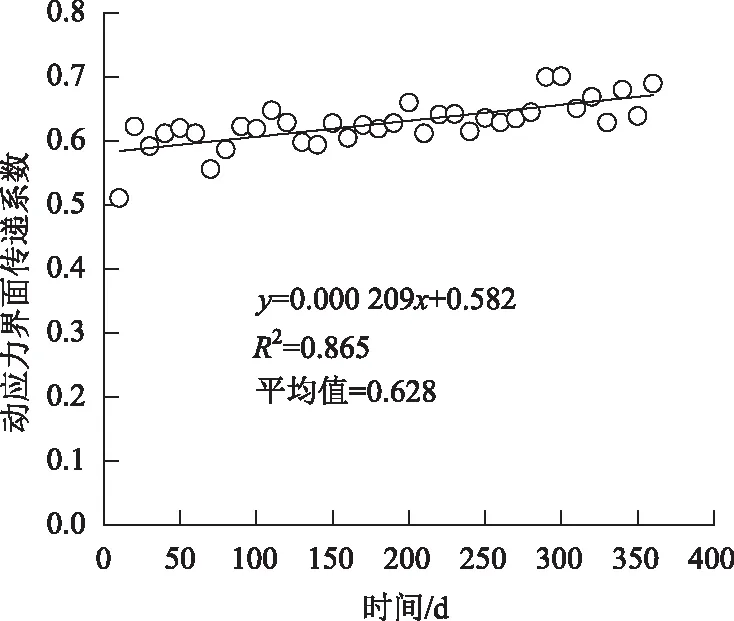
圖3 動應力界面傳遞系數隨時間的變化曲線Fig.3 Curve of dynamic stress interface transfer coefficient vs. time
由圖3可以看出,K39+770斷面動應力界面傳遞系數隨時間變化曲線具有良好的線性擬合特性,其平均值為0.628(明顯小于1.0),這說明在土層界面處發生了動應力突減現象。這主要是由于上硬、下軟兩種土體介質的波阻抗具有差異性所導致的,即當車輛荷載產生的應力波傳遞至土層界面時,反射波的存在使得透射波的能量被消減,進而誘發動應力的突變。由擬合直線的斜率可知,隨著交通運營期的增加,動應力界面傳遞系數的數值略有升高,這說明硬殼層經受車輛荷載長期作用后其力學性能產生了劣化(波阻抗降低),對動應力的界面突減作用在消弱;而擬合直線的斜率值很小,證明硬殼層的力學性能劣化是一個非常緩慢的過程,如果近似按照圖3中擬合直線方程展開預測,當交通運營時間為5.6 a時,動應力界面傳遞系數ξ=1.0,即硬殼層對動應力的突減作用消失。
依照K39+770斷面對監測數據的處理過程,可獲得12個斷面的動應力傳遞系數平均值(其他11個斷面的傳遞系數時程曲線同樣具有較好的線性擬合特性),見表2。
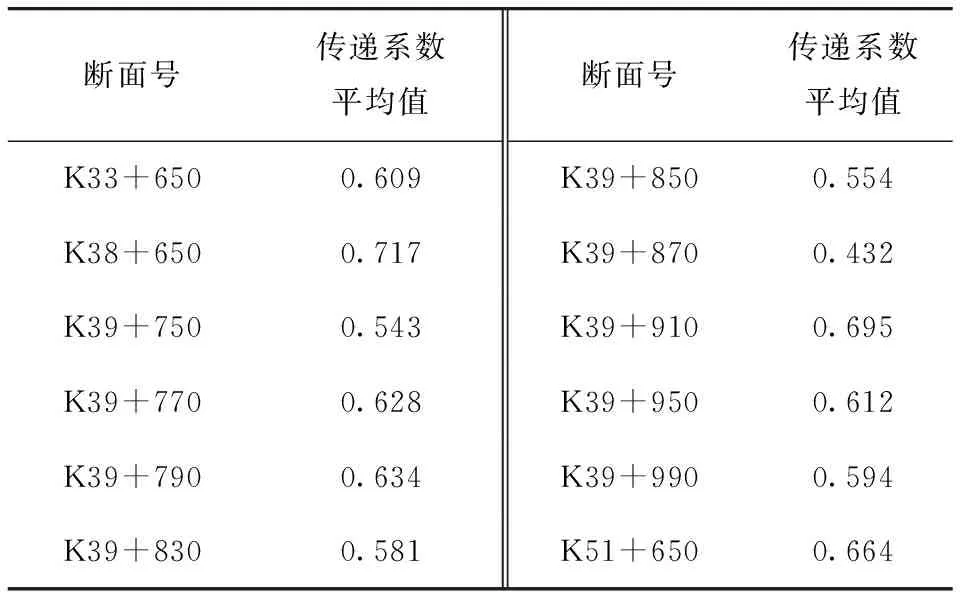
表2 動應力界面傳遞系數平均值Tab.2 Average value of dynamic stress interface transfer coefficient
由表2可知,動應力界面傳遞系數介于0.4~0.6之間的斷面有5個,介于0.6~0.8之間的斷面有7個。因此,土層界面處的動應力突減現象是客觀存在的(以下簡稱界面效應)。工程設計中往往假定土體為均質材料,忽視了層狀地基的界面效應,顯然過高估計了雙層地基中的應力水平,致使設計方案過于保守。同時,界面效應的存在有利于低路堤設計方案的實施,對降低路基土動應力水平起到積極作用。
2 室內動三軸試驗
為了獲得硬、軟土體的臨界動應力值,采用套筒式土鉆分別在硬殼層底部、軟土層頂部采集土樣,制備出若干試樣進行室內動三軸試驗,試樣尺寸:直徑d=39.1 mm,高h=80 mm。試驗采用國產SDT-10型微機控制電液伺服動三軸儀,選用的振動波形為正弦波,加載次數為10萬次,臨界動應力的確定標準為:隨著動應力水平的逐級增大,土樣的累積應變-加載次數曲線將會呈現出穩定型曲線、臨界型曲線、破壞型曲線3種類型,其中臨界型曲線對應的動應力為臨界動應力[23]。選擇圍壓、振動頻率和動應力幅值作為試驗控制條件,見表3。

表3 試驗條件Tab.3 Experimental condition
圖4和圖5分別為軟土和硬土的臨界動應力曲線。
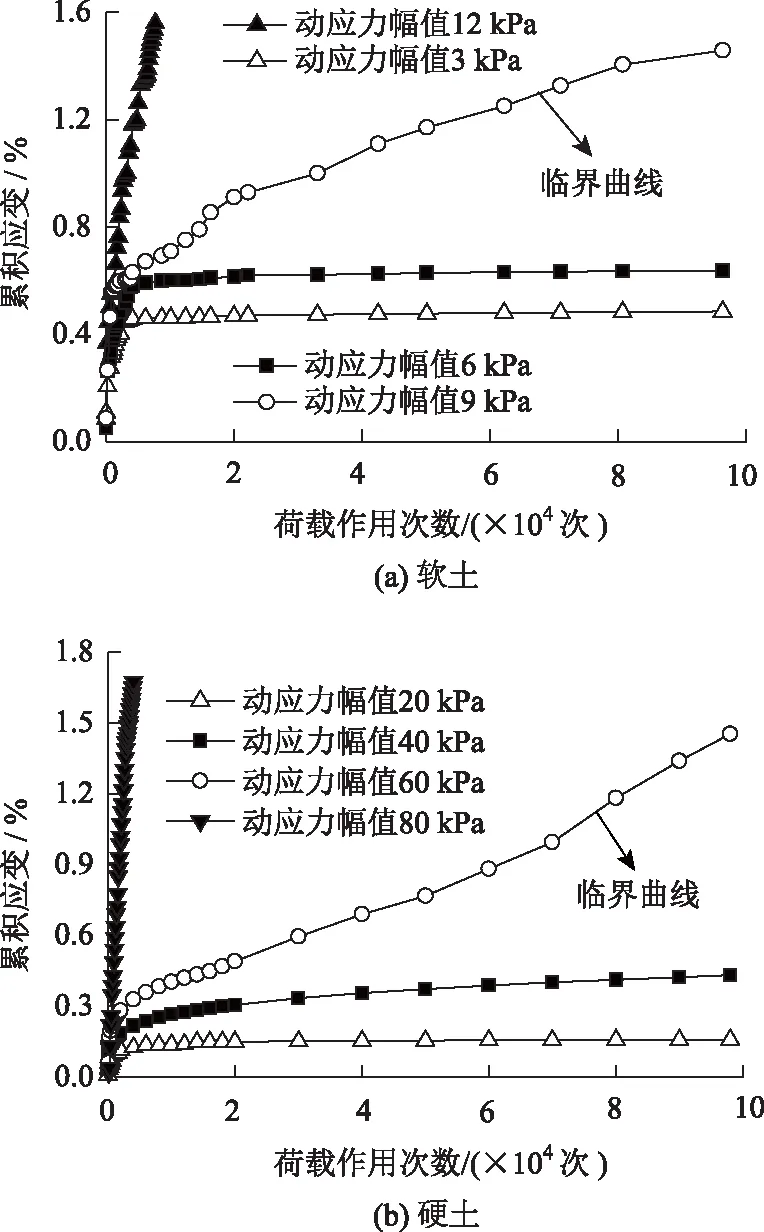
圖4 臨界動應力Fig.4 Critical dynamic stresses
依照圖4,找到臨界曲線對應的動應力幅值,即為該土樣的臨界動應力。經對動三軸試驗數據進行統計分析,得到的結果為:硬土的臨界動應力范圍為50~75 kPa,軟土的臨界動應力范圍為9~21 kPa。
3 運營期路基土損傷評價
由于高速公路的設計使用年限一般為15~20 a,在運營期內路基土承受車輛荷載作用達幾千萬次,屬于典型的低應力水平誘發高周疲勞破壞情況,路基土的力學性能由原狀土逐漸演變為損傷土。從這個認知角度出發,引入路基土損傷評價機制能夠有效反映路基土的運營狀況和受力狀態。
3.1 損傷演化方程構建
文獻[24]應用的Richart-Newmark模型(簡稱R-N模型),是一種非線性疲勞損傷累計模型。該模型能夠有效地考慮荷載幅值和加載次序對材料變形損傷的影響,不僅適用于高周疲勞條件,且還能很好地反映巖土工程材料的非線性變形特征。但是R-N模型以往的應用對象往往為單一土體,為便于雙層地基土體的損傷評價,將其拓展為包含硬、軟兩種土體的整體損傷演化方程,如式(2)所示:
(2)
式中,Dmi為前m個車載序列引起的總土體損傷值,無量綱;nm為第m個車載序列的加載次數;Nm為動應力幅值σdi作用下的土體臨界循環次數;cmi為與土體動應力水平相關的計算參數,無量綱;i代表土體的類型,即:當i=1時表示硬土,當i=2時表示軟土。
兼顧雙層地基土的動力學特點和cmi值的屬性,構建如下cmi值的計算公式:
(3)
(4)
式中,σdcri為土體的臨界動應力;σdi為土體中的動應力幅值;Si為土體的動應力水平。
(1)當σdi=0時,cmi=1,此時式(2)演變成P-M線性損傷累積模型;
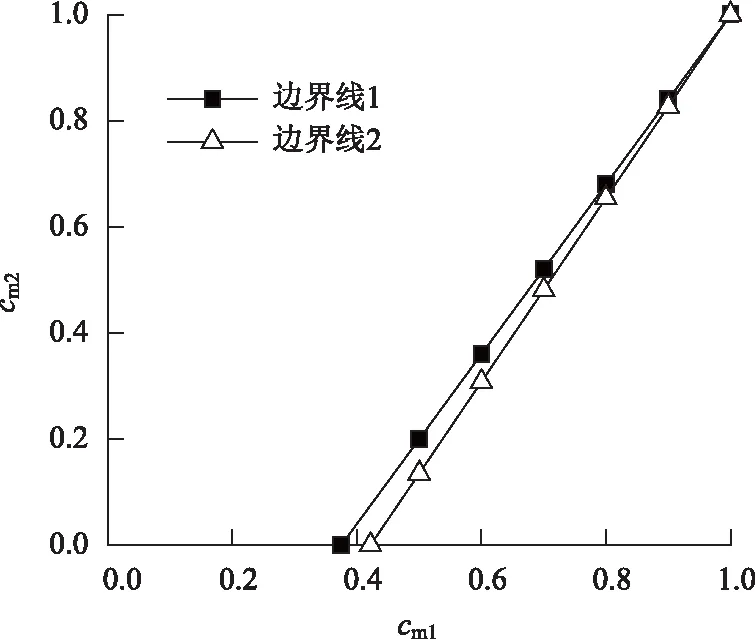
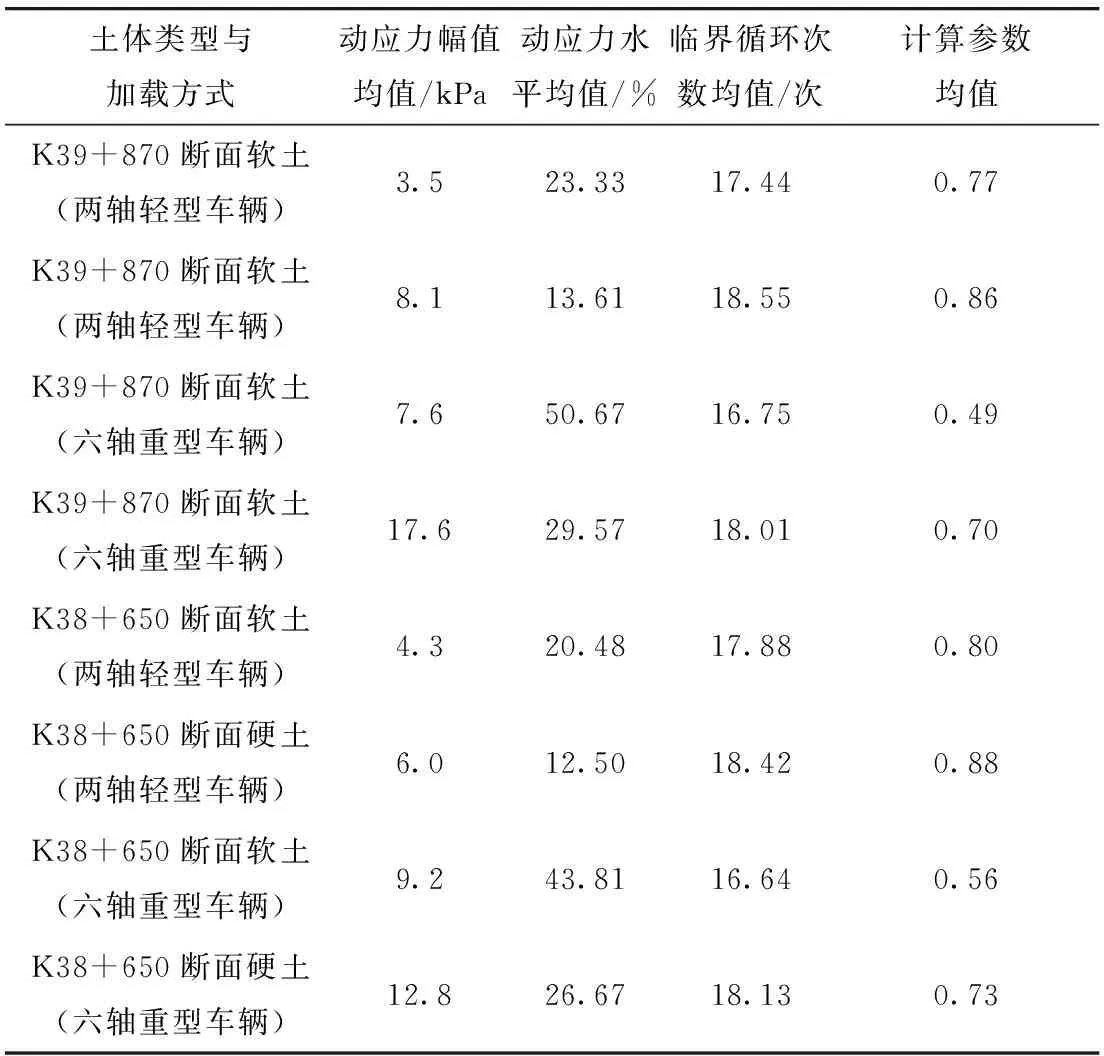
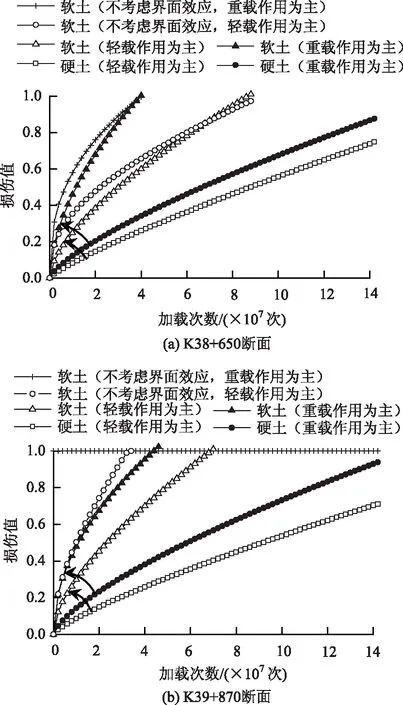
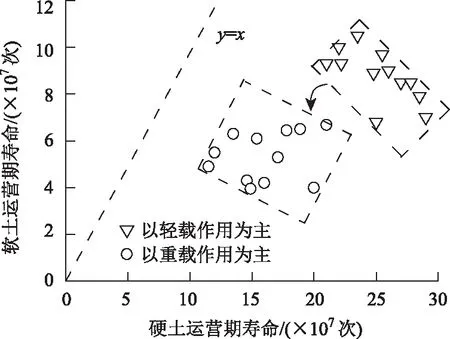
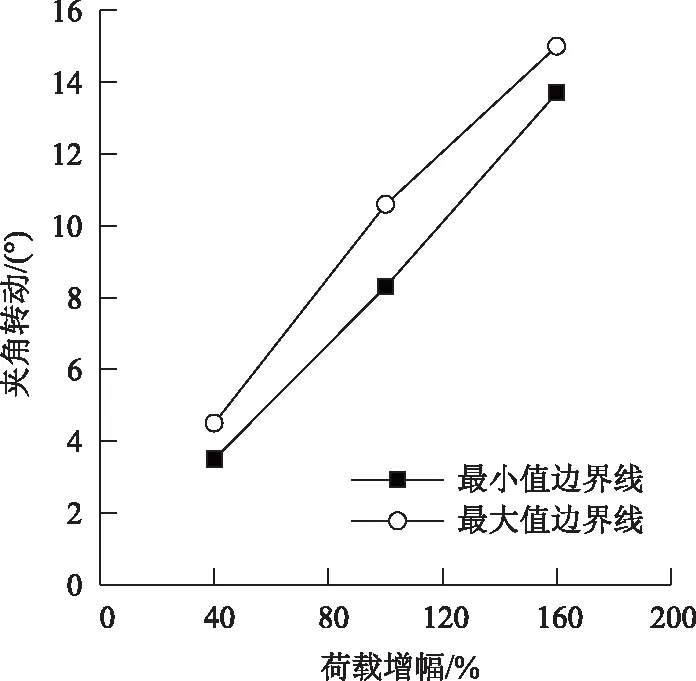
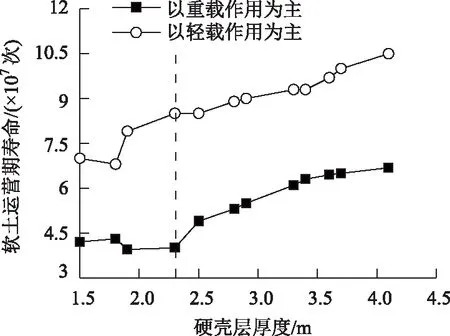
(2)當0<σdi<σdcri時,0 (3)當σdi=σdcri時,cmi=0,Dmi=1,此時土體處于完全損傷狀態。 定義λ為硬、軟土體的動應力水平關聯性系數(同一車輛荷載作用下): (5) 式中,S1為硬土的動應力水平;S2為軟土的動應力水平。 將式(1)和式(4)代入式(5),可得: (6) 式中,σdcr1為硬土的臨界動應力;σdcr2為軟土的臨界動應力。 由式(6)可知,界面動應力傳遞系數ξ與土體臨界動應力比σdcr1/σdcr2均可表現硬、軟土動力特性的差異性,但兩者的變化趨勢正好相反。將表1中的12組現場實測ξ值及臨界動應力的試驗結果代入式(6),得到λ=1.60~1.73,λ值在一個很小的范圍內波動,其波動誤差不超過6.25%,說明硬、軟土的動應力水平具有較強的關聯性。 將式(5)代入式(3)可得: cm2=1-λ(1-cm1), (7) 式中,cm1為硬土損傷模型的計算參數;cm2為軟土損傷模型的計算參數。 利用式(7)可以得到硬、軟土模型計算參數之間的關系曲線,如圖5所示。兩種參數取值范圍局限于兩條邊界線之內,可見兩者也具有較強的相關性。 圖5 R-N損傷模型參數關聯曲線Fig.5 Relevance curves of R-N damage model’s parameters 為得到高速公路準確的加載情況,需要對車輛載荷譜進行統計分析。為研究方便,分別以100%輕型車輛作用、80%輕型車輛+20%重型車輛作用(以下簡稱輕載作用為主)、50%輕型車輛+50%重型車輛作用、20%輕型車輛+80%重型車輛作用(以下簡稱重載作用為主)4種工況展開計算,其中20%,50%,80%和100%指加載車輛出現的概率。以K39+870斷面和K38+650斷面為例,其R-N模型計算參數見表4,土體損傷曲線如圖6所示。 表4 R-N損傷模型計算參數Tab.4 Calculation parameters of R-N damage model 圖6 土體損傷曲線Fig.6 Curves of soil damage 定義硬、軟土損傷曲線在原點處切線之間的夾角為θ(以下簡稱夾角),該夾角的數值變化可分解為兩部分:數值不變而位置發生轉動,以及位置不變而數值發生改變。將第1部分轉動的角度用β表示(以下簡稱夾角轉動),將第2部分數值的改變量用Δθ表示(以下簡稱夾角增量)。將圖7導入CAD軟件中,借助CAD軟件的繪圖和測量功能,可以較為便捷地獲取到夾角θ和夾角轉動β的數值大小。在圖7中只需將各損傷曲線與損傷值Dmi=1對應的直線取交點,該交點的橫坐標即為運營期壽命的數值大小。 圖7 硬、軟土運營期壽命的統計關系Fig.7 Statistical relation between operation period lives of hard soil and soft soil 由圖7可知,對于K38+650斷面而言,輕載作用為主時夾角θ1=32.2°,重載作用為主時夾角θ2=41.5°,θ2相對θ1繞原點逆時針發生夾角轉動β=8.8°,同時產生夾角增量Δθ=9.3°;對于K39+870斷面而言,輕載作用為主時夾角θ3=35.1°,重載作用為主時夾角θ4=39.2°,θ4相對θ3繞原點逆時針發生夾角轉動β=9.8°,同時產生夾角增量Δθ=4.1°。K38+650斷面、K39+870斷面的夾角轉動β和夾角增量Δθ均未超過10°,但是兩者的運營期壽命(當Dmi=1時對應的加載次數)降低值卻相差很大,前者降低4 200萬次,后者降低2 700萬次。可見,夾角轉動β與夾角增量Δθ對路基運營期壽命十分敏感,是評價路基損傷的兩個關鍵指標(其他10個斷面的計算結果也得出了相似結論)。 值得關注的是,在不考慮界面效應且輕載作用為主時,軟土的運營期壽命為8 700萬次(圖7(a))和3 500萬次(圖7(b));在不考慮界面效應且重載作用為主時,軟土的運營期壽命僅為3 800萬次(圖7(a))和0次(圖7(b))。計算結果與工程實際嚴重不符,這說明雙層地基設計中不能忽視界面效應的影響。 夾角轉動β、夾角增量Δθ及運營期壽命用來表征土體損傷演化特征比較直觀,但用于工程設計中操作性不強,下面對12個斷面的土體損傷曲線信息進行統計分析。 分別以硬、軟土的運營期壽命為橫、縱坐標建立坐標系,如圖7所示。 由圖7可知,所有數據點均在y=x直線的下方,說明在相同工況下軟土的運營期壽命短于硬土,即軟土的損傷程度大于硬土,路基的總體運營期壽命取決于軟土層,軟土層是控制路基穩定性的關鍵土層,這與文獻[25]的結論基本一致。由式(6)的計算結果不難得出,這是軟土動應力水平均高于硬土所導致的結果。 由于下臥軟土層并不位于地表,且車輛荷載傳遞至此的動應力數值很小,其潛在的破壞行為和對路基穩定性的影響程度往往被忽視,這一點在雙層地基設計中應引起高度重視。 以100%輕型車輛作用為基準,將12個斷面其他3種工況產生的夾角轉動β最大值、最小值與荷載增幅(例如,輕載作用為主較100%輕型車輛作用的荷載增幅為40%)繪制在同一個坐標系,如圖8所示。 圖8 夾角轉動與荷載增幅的擬合曲線Fig.8 Fitting curves of intersection angle rotation and load increment 由圖8可知,夾角轉動β與荷載增幅之間基本呈線性關系,說明夾角轉動β主要受車輛荷載大小影響,車輛荷載加大時β為逆時針,反之為順時針。車輛荷載每增幅10%夾角轉動β相應增加約1°,運營期壽命降低約270~480萬次,這為估算超載運營工況的雙層地基壽命提供了依據。 此外,從圖8的兩類數據點分布特征看,輕載作用為主的數據區域向重載作用為主的數據區域發生了逆時針偏轉,這說明車輛荷載的增加使得軟土層的運營期壽命縮短速度快于硬土,導致整個路基的運營期壽命呈現加速降低的趨勢。 由于傳遞路徑的增加,硬殼層厚度直接影響到車輛荷載傳遞至軟土層的動應力大小,繼而影響到軟土的運營期壽命。將12個斷面的硬殼層厚度與對應的軟土層運營期壽命(包括輕載作用為主和重載作用為主兩種工況)建立在同一坐標系下,如圖9所示。 圖9 硬殼層厚度與軟土運營期壽命關系曲線Fig.9 Curves of hard crust’s thickness vs. soft soil’s operation period life 由圖9可知,兩種工況下的關系曲線基本呈上升走勢,即隨著硬殼層厚度的增加,軟土運營期壽命得以延長。重載作用為主工況下曲線相對平緩,主要是由于重載交通導致硬殼層性能劣化嚴重,界面效應減弱明顯,致使傳遞至軟土層中動應力增加,與硬殼層厚度增加引發動應力減小兩者呈抵消之勢。 在開始階段兩條曲線趨于平緩,并出現了小幅波動,這主要是因為硬殼層厚度較小,承載能力相對薄弱,其力學性能劣化明顯,導致上述動應力抵消現象顯著造成的。找出兩條曲線共有的穩定上升段起點,對應的硬殼層厚度為2.3 m,該數值可以作為高速公路工程設計中的重要參考值。 圖10 夾角增量平均值與壓縮模量比的擬合曲線Fig.10 Fitting curve of average intersection angle increment and compression modulus ratio 經過10余年的通車檢驗,發現在利用天然硬殼層作為路基持力層的路段中,其硬殼層厚度超過2.3 m 且硬、軟土體壓縮模量比大于4.6的斷面,其路面出現明顯裂縫、車轍的情況很少,且路基監控斷面的沉降量未超過預先設定的報警值。2013年7月至8月對重載交通作用較為頻繁的上覆厚硬殼層軟土路基段展開現場調查,結果表明,5%的區段運營效果較差或一般,15%的區段運營效果較好,80%的區段運營效果優良。 因此,對于同時滿足上述兩個條件的高速公路路基斷面,建議在工程設計中應優先考慮利用天然硬殼層作為路基持力層,而非直接采用地基處理的方式(具體設計時也要兼顧路堤高度、硬殼層剛度等因素的影響)。 (1)借助工程現場實測數據的統計結果,揭示出上硬下軟土層界面處存在明顯的界面效應,即動應力突減現象。而動應力界面傳遞系數的引入,有助于客觀估計動應力在層狀地基中的傳播規律。 (2)依據硬、軟土體臨界動應力比值和動應力界面傳遞系數,推演得出上硬下軟土層的動應力水平具有較強的關聯性,繼而將兩種土體的損傷模型計算參數建立起邏輯關系,這為構建雙層地基動力損傷演化方程提供了有效的解決途徑。 (3)軟土層是誘發雙層地基失穩的關鍵層。車輛荷載的增加使得軟土層的運營壽命縮短,且縮短速度快于硬土,導致整個路基的運營期壽命加速降低。硬殼層厚度超過2.3 m,且硬、軟土體壓縮模量比超過4.6時,在高速公路工程設計中應優先考慮利用天然硬殼層作為地基持力層。3.2 兩種土體計算參數的關聯性

3.3 硬、軟土體損傷演化特征
4 工程設計指導
4.1 路基失穩關鍵層的確定
4.2 車輛荷載增幅影響
4.3 硬殼層厚度的利用范圍
4.4 硬、軟土壓縮模量比拐點值
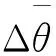

5 結論

