季節凍土區公路隧道三維溫度場時空分布規律

張玉偉，宋戰平，賴金星，李又云

(1.西安建筑科技大學 土木工程學院，陜西 西安 710055；2. 西安建筑科技大學 陜西省巖土與地下空間工程重點實驗室，陜西 西安 710055；3.長安大學 公路學院, 陜西 西安 710064)

0 引言

我國高緯度和高海拔地區均屬于典型的季節性凍土區，這些地區溫度周期性變化常常對建筑物造成凍融損害[1-5]。對于隧道工程而言，襯砌容易發生凍脹破壞，出現襯砌漏水、路面結冰等凍害[6-10]。探明隧道溫度場規律是解決凍害的前提。丁浩[11]等通過現場測試分析了隧道圍巖和襯砌溫度變化規律；張學富[12]等自編程序分析了風火山隧道環境-圍巖熱傳導變化規律；譚賢君[13]等考慮通風影響，推導了圍巖溫度場模型；Li[14]等分析了隧道開挖后圍巖溫度場的分布、初期支護以及二次襯砌的溫度變化規律；Zhou[15]等基于季節凍土隧道，建立了保溫層優化計算模型；Zhang[16]等研究了熱棒在淺埋寒區隧道工程中應用，并分析其溫度變化特性；Zeng[17]等分析了對流傳導耦合效應下的隧道溫度場變化規律；Jun[18]等采用現場測試手段分析了隧道內部冬季溫度變化規律。寒區隧道凍害是凍脹力周期性作用于襯砌，導致襯砌疲勞劣化而出現病害，凍脹力又由于溫度變化而產生。因此建立隧道三維溫度場模型、明確溫度演化規律是解決寒區隧道凍害問題的基礎。

關于寒區隧道溫度場研究多以數值模擬手段為主，基于現場測試的溫度場研究則相對較少，且測試數據完整性尚顯不足，在現場測試基礎上進行三維溫度場的研究更是很少涉及。為建立寒區隧道三維溫度場模型，本研究采用溫度傳感器開展了現場監測，獲得隧道環境溫度和圍巖溫度變化規律，并推導了圍巖凍結深度隨隧道進深和時間的變化規律。通過測試結果分析，建立了三維溫度場數學模型，模型可以預測溫度場的時空變化特征，研究結果可為寒區隧道保溫設計提供依據，也為進一步研究凍脹力提供了基礎。

1 現場測試分析

1.1 工程概況

某寒區公路隧道位于川西高原，海拔高程4 200 m 左右，隧道長度2 745 m，為單洞雙車道的二級公路隧道，隧道斷面凈空尺寸(寬×高)為 9 m×5 m。隧址區屬于青藏高原氣候，夏季溫和，冬季寒冷，極端高溫超過30 ℃，極端低溫低于-20 ℃。5月至10月多為東南風，最大風速大于5.7 m/s，頻率27%；11月至次年4月多偏北風，最大風速20 m/s，平均風速4 m/s，頻率23%，隧道內風速多為3～5 m/s。隧址區域內水系發育，受圍巖溫度場變化，發生凍害的可能性較大。

1.2 測試方案

隧道溫度場主要指洞內環境溫度場和圍巖溫度場，因此測試主要針對洞內溫度和圍巖溫度展開，隧道洞口段氣溫變化明顯，而越往隧道內部，溫度變化越小，因此主要布置在洞口段，第1個斷面位于洞口處，依次向內分別間隔20，30，50 m和100 m。斷面布置見圖1和圖2，其中5個測試斷面均進行環境溫度測試，選取斷面1和斷面4進行圍巖溫度測試，圍巖溫度傳感器采用湖南某公司生產的YH5101型溫度傳感器。主要技術參數為：理論可工作溫度區間為-50～50 ℃，靈敏度為0.1 ℃。布設方法為在圍巖打4 m深的孔，將溫度傳感器間隔1 m 固定在1根鋼筋上，然后插入到孔中，用砂漿回填(見圖2)。采用某公司配套的自動化采集系統，圍巖內溫度值監測頻率為每天4次，測定時間為每天2：00，8：00，14：00，20：00。

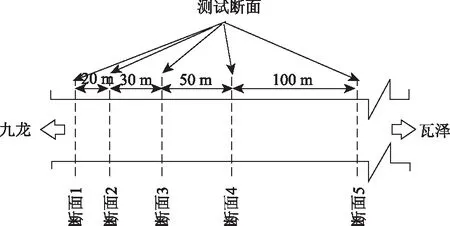
圖1 測試斷面Fig.1 Test section

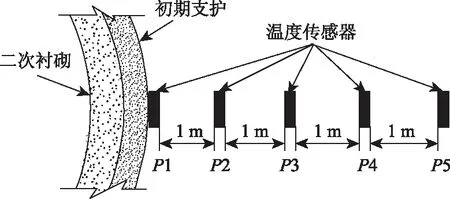
圖2 圍巖溫度測點布設Fig.2 Layout of temperature measuring points on surrounding rock

1.3 測試結果分析

隧道環境溫度通過溫度計直接測得，取每月中日平均溫度的均值作為隧道環境溫度的月平均值。圖3和圖4分別給出了不同斷面環境溫度隨時間和進深的變化規律。圖3可以看出5個斷面的環境溫度均呈正弦函數規律變化，但5個斷面的最高溫度和最低溫度不同，即正弦函數的振幅不同，圖4表明隧道洞口段溫度隨時間變化更加明顯，越往隧道內部，溫度變化越小，即溫度振幅隨著隧道進深增加而逐漸趨于穩定，說明隧道具有一定自保溫效果，洞口段應著重保溫。

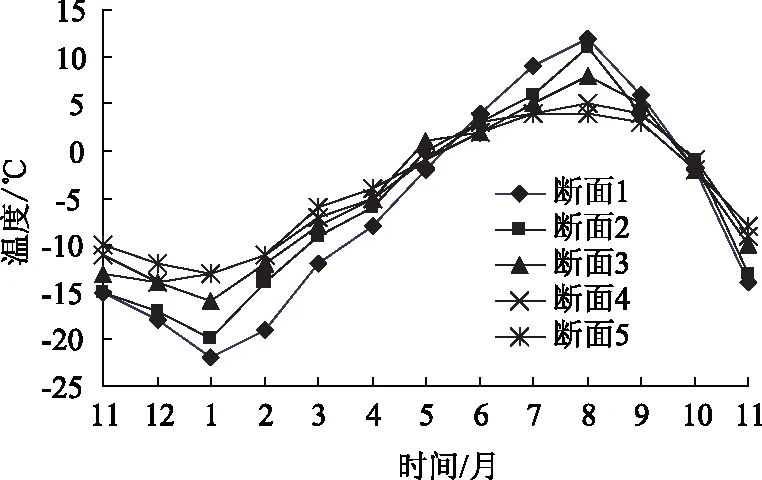
圖3 環境溫度隨時間變化Fig.3 Ambient temperature varying with time

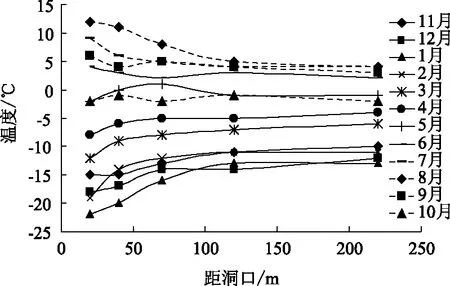
圖4 環境溫度隨進深變化Fig.4 Ambient temperature varying with length

取每月日均溫度的平均值作為月平均溫度，圖5給出了斷面1不同徑向深度圍巖溫度隨時間變化規律，圖6給出了圍巖溫度隨徑向深度的變化規律。圖5表明某一斷面處圍巖徑向溫度受環境溫度的影響也呈正弦函數變化，且隧道圍巖徑向深度的增加影響效果逐漸減小，越靠近襯砌表面正弦規律變化越明顯，測點4,5溫度基本不變說明徑向深度達到3 m時基本不受影響，溫度影響范圍主要集中在距襯砌2 m范圍內。圖6表明圍巖溫度隨徑向深度的變化關系，在圍巖受影響的2 m范圍內負溫月份的溫度與徑向深度近似呈線性關系，隨著深度增加溫度逐漸趨于原始圍巖溫度。

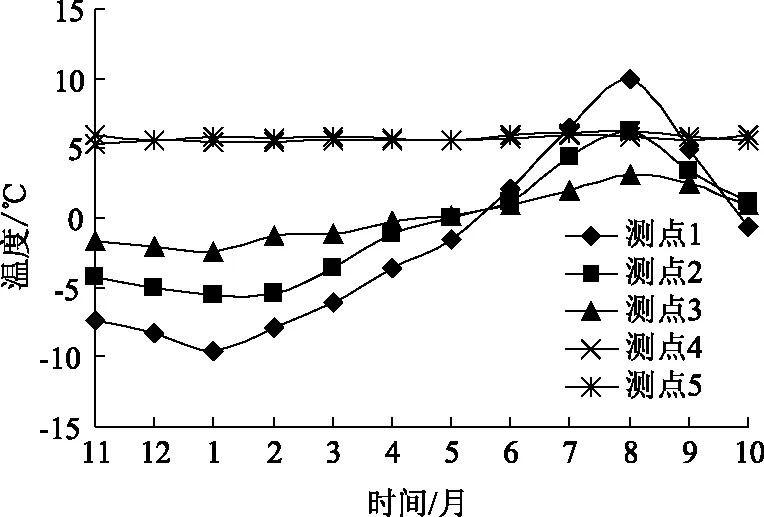
圖5 圍巖溫度隨時間變化Fig.5 Temperature of surrounding rock varying with time

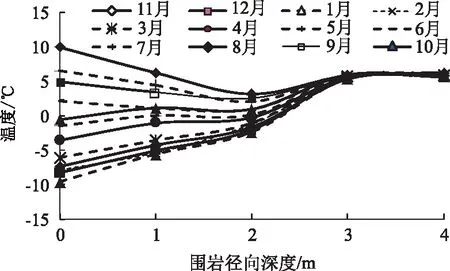
圖6 圍巖溫度隨徑向深度變化Fig.6 Temperature of surrounding rock varying with radial depth

2 溫度場時空分布模型

2.1 環境溫度場

通過分析結果可看出環境溫度隨時間呈正弦規律變化，環境溫度可表達為[7]：

(1)

式中，Tm為某一斷面的溫度；T0為平均溫度；A0為振幅；t為月份；t0為相位。式(1)即描述了環境溫度隨時間的正弦函數演化特征，式(1)中未涉及隧道進深，由測試結果我們知道T0和A0均隨隧道進深變化而改變，如果得到T0和A0隨隧道進深的函數關系，并代入式(1)即可得到環境溫度的時空變化規律。下面根據現場測試數據分析T0和A0與隧道進深的變化關系。

表1給出振幅A0與平均溫度T0隨隧道進深變化規律，為了得到近似函數關系，采用非線性擬合回歸分析得到兩者隨隧道進深的函數表達式，通過擬合圖7為近似擬合效果，通過圖7可看出，平均溫度隨隧道進深呈近似線性關系，振幅隨隧道進深呈近似對數關系，可采用線性函數和對數函數近似描述評價溫度和振幅，見式(2)，式(3)。

表1 振幅與平均溫度隨進深的變化Tab.1 Amplitude and average temperature varying with length

圖7 環境平均溫度和振幅Fig.7 Average ambient temperature and amplitude

Ay=alnx+b，

(2)

Ty=cx+d，

(3)

式中，a,b,c,d分別為擬合值，本研究中a取-3.96，b取 29.14，c取0.007 3，d取-5.14；x為距洞口距離。將式(2)，式(3)代入式(1)得：

(4)

式(4)即為隧道環境溫度時空分布規律(圖8)。

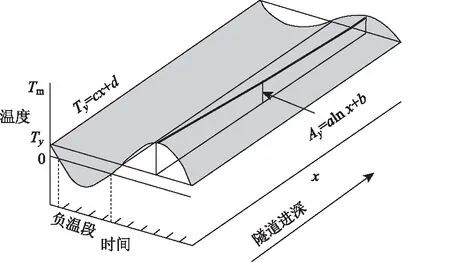
圖8 環境溫度場時空分布圖Fig.8 Spatial-temporal distribution of ambient temperature field

2.2 圍巖徑向溫度場

圍巖溫度場受環境溫度的影響，變化規律較為復雜。圍巖溫度場可通過傳熱學原理推導得出嚴格的解析解[13-14]，但需要做諸多假設，且推導過程繁瑣，結果表達也相當復雜，實際應用不是很方便，本研究從實用的角度出發，依據現場測試結果，旨在給出圍巖溫度場的擬合經驗公式，文獻[7]做過類似的工作，但是只給出了某一斷面處圍巖溫度沿徑向的變化規律，沒有建立圍巖溫度場與軸向深度時間的三維關系。本研究通過圍巖溫度測試成果，建立圍巖溫度場表達式。圍巖溫度與隧道進深、時間和圍巖徑向深度3個變量有關，屬四維問題，而圍巖溫度與環境溫度密切相關，因此首先建立圍巖溫度與環境溫度的關系，即暫不考慮隧道進深的影響，減少一個變量。

由圖5可看出徑向一定深度范圍內圍巖溫度也呈正弦函數規律變化，即圍巖溫度場也可以用式(1)描述，考慮某一斷面處圍巖溫度場，圍巖平均溫度和振幅與徑向深度的關系見表2，并將兩者關系繪制于圖9。

圖9中可看出圍巖平均溫度和振幅均隨徑向深度有一定關系，文獻[9]也指出年溫度振幅隨圍巖徑向深度呈指數規律降低，一定深度后振幅為0，圍巖平均溫度呈對數規律變化，因此文中假定以上規律進行擬合：

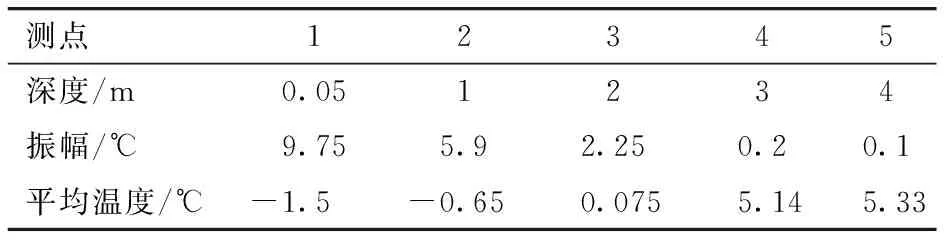
表2 振幅與平均溫度隨徑向深度的變化Tab.2 Amplitude and average temperature varying with radial depth

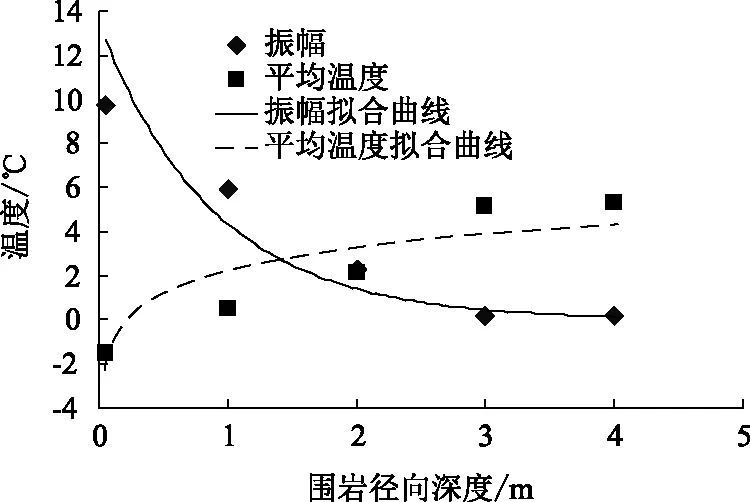
圖9 圍巖振幅與平均溫度Fig.9 Amplitude and average temperature of surrounding rock

Aw=a′exp(b′r)，

(5)

Tw=c′lnr+d′，

(6)

式中，a′,b′,c′,d′分別為擬合值，文中a′取13.42，b′取-1.13，c′取1.48，d′取2.26，r為圍巖徑向深度Aw為圍巖的平均溫度。將式(5)～(6)代入式(1)得：

(7)

式中,Tw為某一斷面處圍巖溫度隨徑向深度和時間的變化規律;t′0為圍巖溫度月相位。

可以看出，式(7)給出了某一斷面處圍巖溫度與時間和圍巖徑向深度的關系，并未建立與隧道軸向深度的關系，我們知道圍巖溫度與環境溫度密切相關，而環境溫度沿隧道進深關系為對數關系，因此假設圍巖溫度與軸向深度關系也呈近似對數關系：

Tw(x)=αlnx+β，

(8)

式中α,β為擬合參數。式(7)和式(8)共同建立了圍巖溫度與時間、徑向深度、隧道軸向深度的關系。

事實上我們主要關心圍巖凍結月份(11月至次年3月)的溫度變化，分析圖6可以看出，圍巖凍結月份溫度隨徑向深度增加逐漸增大，在2 m范圍內可近似認為是線性的，隨著徑向深度進一步增大，溫度逐步趨于原始圍巖溫度。因此可假設圍巖在受影響的范圍內溫度也是近似線性變化的，可直接建立圍巖溫度與環境溫度的關系。

Tw=k1Tm+k2r，

(9)

式中，k1為熱量散失及滯后效應引起的溫度損失系數；k2為擬合系數；r為圍巖徑向深度。其中k1可通過數值分析或室內試驗進行確定。

2.3 凍結深度的確定

在溫度場基礎上可進一步確定圍巖凍結深度，從而為凍脹力研究和防凍保溫設計提供理論依據，在季凍區圍巖的凍結深度可由Stephen公式確定：

(10)

Qw=qρd(ω-ωc)，

(11)

式中，hw為凍深；λw為導熱系數；∑Tw為凍結指數；Qw為單位體積相變潛熱；q為水結冰相變潛熱；ρd為干密度；ω為總含水率；ωc為含冰量。

式(10)表明圍巖凍結深度與圍巖凍結指數相關，而圍巖凍結指數與隧道環境溫度有關，隧道環境溫度具有時空變化特征，可由式(4)來表示，溫度變化見圖10。式中，x1=(12/2π)arcsin[-(cx+d)/(alnx+b)]，圍巖凍結指數可由積分求得：

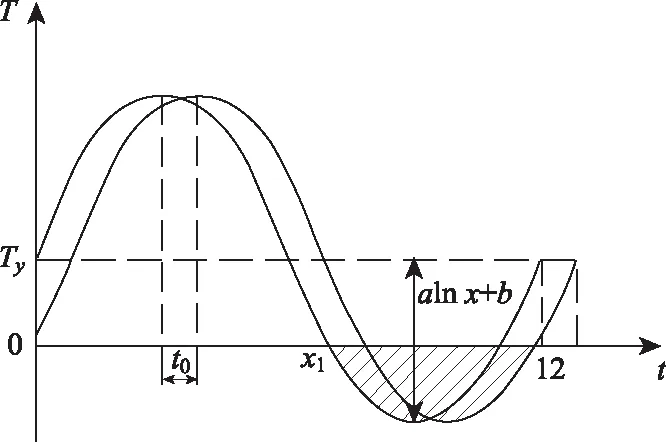
圖10 溫度變化示意圖Fig.10 Schematic diagram of temperature change

(12)

聯立式(11)～式(13)可得圍巖最大凍結深度隨隧道深度的變化：

(13)

式(13)即為圍巖凍結深度隨隧道進深的變化關系，但無法描述凍結深度隨時間的變化關系，實際中圍巖凍結深度與環境溫度密切相關，前述分析表明隧道環境溫度隨時間呈正弦規律變化，因此，可近似認為圍巖凍結深度也隨時間呈正弦規律變化，即：

(14)

式(13)和式(14)即描述了圍巖凍結深度隨隧道進深和時間的變化規律。

3 結果對比分析

3.1 環境溫度

圖11和圖12分別給出環境溫度隨時間變化規律和空間變化規律的模型計算值與實測值對比，可以看出計算值與實測值總體吻合較好，隨軸向深度溫度變化幅度逐漸減小，不同深度的平均溫度與振幅擬合函數能夠很好地描述環境溫度變化，隨進深增加有自保溫效果，保溫設計時應予以考慮。

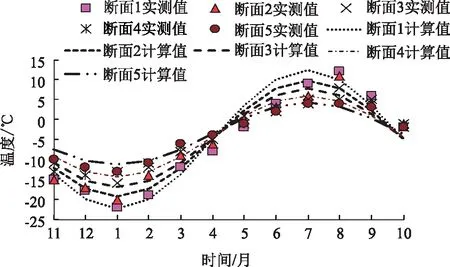
圖11 環境溫度隨時間變化對比Fig.11 Comparison of Ambient temperatures varying with time

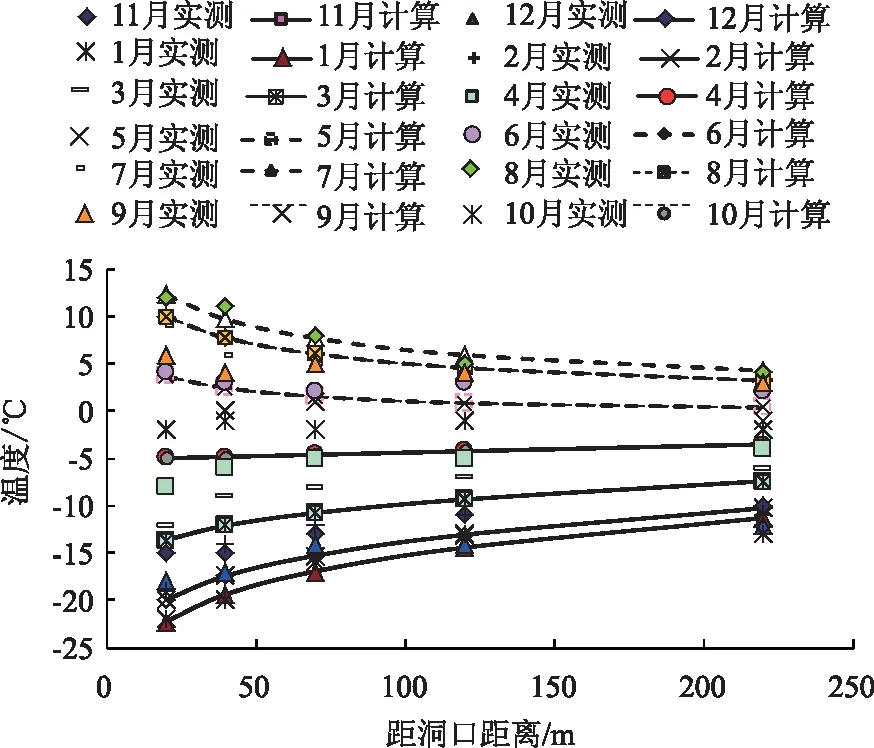
圖12 環境溫度隨進深變化對比Fig.12 Comparison of Ambient temperatures varying with length

3.2 圍巖溫度

圖13和圖14為圍巖溫度隨時間和圍巖徑向深度的對比，可看出受環境溫度的影響圍巖徑向一定范圍內溫度也呈正弦規律變化，隨徑向深度增加變化逐漸減小，距離襯砌表面越近變化越明顯，模型預測值與現場測試值吻合較好，說明本研究模型能夠準確預測圍巖溫度隨時間和圍巖徑向深度的變化規律，通過模型可初步預測某一斷面處圍巖徑向溫度。

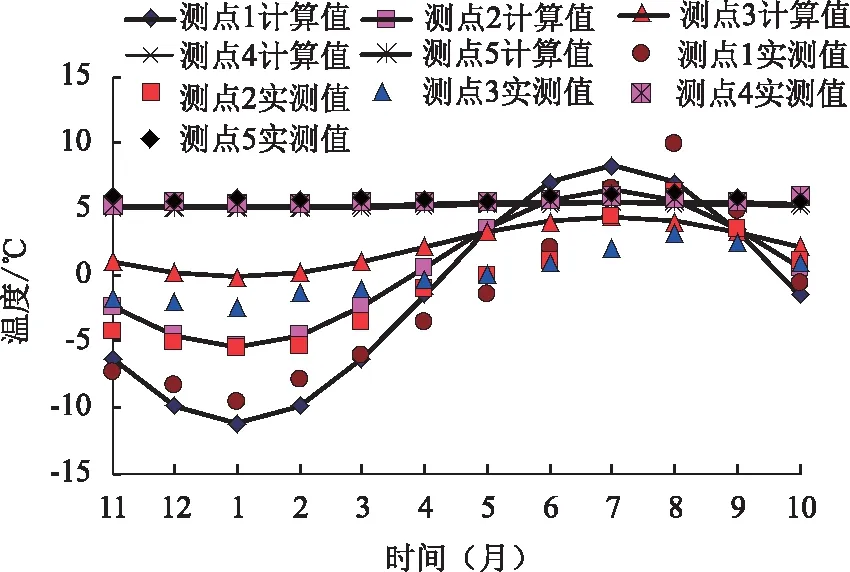
圖13 圍巖溫度隨時間變化對比Fig.13 Comparison of surrounding rock temperatures varying with time

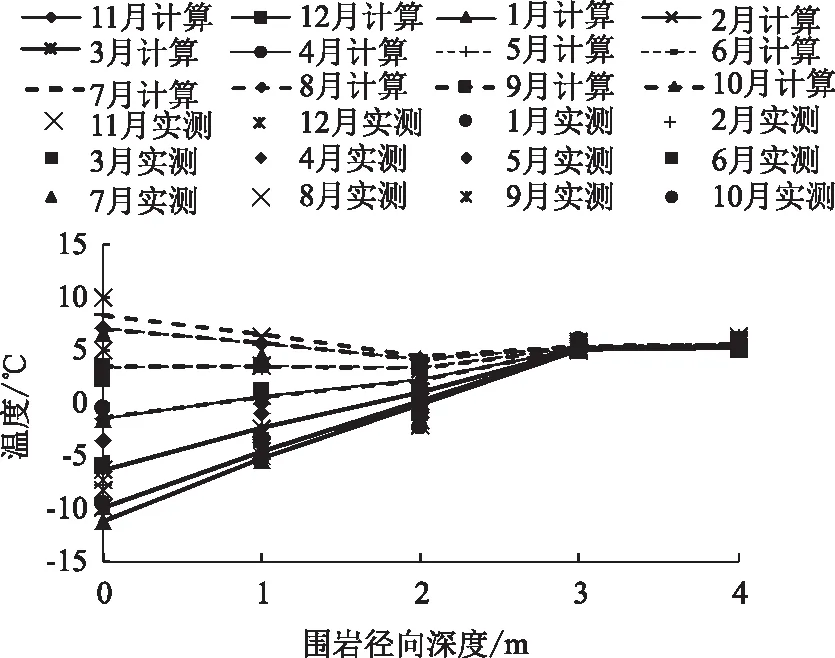
圖14 圍巖溫度隨徑向深度變化對比Fig.14 Comparison of surrounding rock temperatures varying with radial depth

3.3 凍結深度

由設計資料，λw取1.12，平均氣溫T0為1.1 ℃，溫度振幅A為年溫度差一半取18 ℃，水結冰相變潛熱q為333.56 kJ/kg，圍巖干密度ρd為2.35 kg/m3，圍巖總含水率ω為46.2%，凍結圍巖中含冰量ωf為41.7%，由式(13)求得圍巖凍結深度。圖15為圍巖凍結深度隨隧道軸向深度的變化規律，凍結深度隨軸向距離的增加而逐漸減小，斷面1為1.83 m，斷面5為1.45 m，由前文環境溫度結果可以看出越往隧道內部環境溫度越高，隧道有一定的自保溫效果，因此圍巖凍結深度逐漸減小，與模型計算結果相吻合；通過斷面1和斷面4的圍巖溫度測試結果也可以看出，因為斷面4位于隧道內部，斷面1圍巖凍結深度要大于斷面4，這也與模型計算結果相一致。

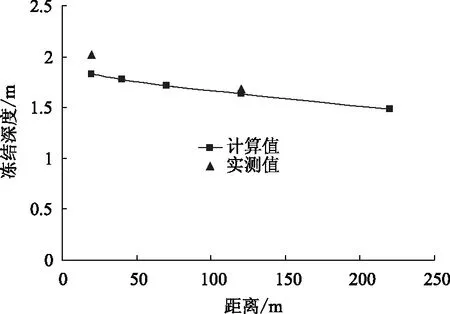
圖15 凍結深度隨軸向距離變化Fig.15 Frozen depth varying with axial distance

現場測試和模型計算結果說明，寒區隧道洞口段環境溫度受環境溫度影響周期性變化明顯，隨著軸向深度的增加，溫度振幅減小，隧道有自保溫效果，圍巖溫度在徑向一定范圍內受環境溫度的影響也呈正弦函數周期性變化，這種影響隨著圍巖深度增加逐漸減弱，影響范圍主要集中在2 m范圍內，基于溫度場進一步求解圍巖凍結深度，其規律在空間上表現為隨著軸向深度增加逐漸減小，隧道洞口段應加強保溫措施。溫度場分布規律一方面為寒區隧道保溫設計提供理論依據，另一方面也為下一步研究凍脹力提供了理論基礎。

4 結論

(1)依托某寒區隧道工程現場布設若干測試斷面，分別測試了隧道洞內溫度、圍巖徑向溫度，結果表明，隧道洞內溫度與時間和軸向距離呈三維變化關系，同一斷面溫度與時間呈正弦函數變化，同一時間時平均溫度與軸向距離呈線性變化，溫度振幅與軸向距離呈對數變化，隧道洞內溫度在洞口段200 m范圍內變化劇烈，圍巖溫度在2 m范圍內變化明顯。

(2)以現場測試成果為基礎建立寒區隧道洞內溫度場時空分布模型和圍巖徑向溫度場模型，在此基礎上分析圍巖凍結深度變化規律，洞口處斷面1最大為1.83 m，隨著隧道進深增加，圍巖凍結深度逐漸減小,斷面5僅為1.45 m，與現場測試結果基本吻合。

(3)建立了三維溫度場模型，當類似寒區隧道缺乏溫度實測資料時,可根據本研究的方法對溫度場進行初步預測。文中計算模型中的參數是根據本隧道測試結果得出的，對于氣候條件相似的寒區隧道具有一定的適用性，但是對于氣候溫度相差較大的隧道具有局限性，建議以后有條件增加溫度場測試工作，對模型中參數進一步修正，并建立氣候溫度條件與模型參數的對應關系，使其具有更廣泛的適應性。