借用思維導圖 提升思維能力
趙旭
在小學數學教學中,能夠借助思維導圖,可幫助學生梳理所學的內容,理清不同數學知識之間的關聯和邏輯關系,發展學生的數學思維能力。
一、再現知識脈絡,濃縮教材要點
教師可以結合教材內容設計思維導圖,濃縮數學概念,讓學生直觀地看到數學知識之間的脈絡。
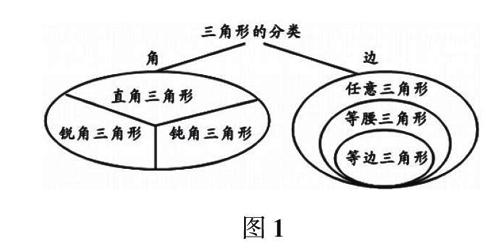
教學部編版教材四年級上冊《三角形的分類》時,為了讓學生清晰地梳理不同三角形的分類方法,筆者讓學生圍繞角和邊兩個維度對三角形展開探究。學生經過交流合作,發現根據角來分類,能夠將三角形分成銳角三角形、直角三角形和鈍角三角形3種類型;根據邊來分類,可以將三角形分成三邊不相等的三角形,兩邊相等的三角形和三邊都相等的三角形3種類型。根據角分成的3類,它們之間是什么關系?根據邊分成的3類,它們之間是什么關系呢?根據角和邊分別分成的3類之間,又是什么關系?學生經過觀察與思考,發現根據角分成的3類之間是并列關系,根據邊分成的3類之間是包含關系,而根據角和邊分別分成的3類之間,又是并列關系。這樣表述十分抽象,學生理解起來有困難,所以筆者借助直觀形象的思維導圖,給學生出示三角形相關知識之間的關聯,如圖1所示。
從思維導圖中,學生不僅能夠清晰地看到不同分類方法之間的數學關系,還能夠看出三角形相關分類的本質內涵。
二、經歷推演過程,呈現思維路徑
教師運用思維導圖幫助學生經歷推演過程,能清晰地呈現出思維的發展路徑,培養學生分析問題和解決問題的能力。
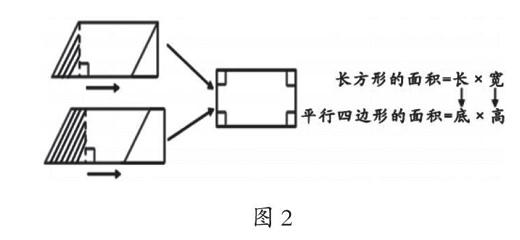
在執教部編版五年級上冊《平行四邊形的面積》時,筆者讓學生從長方形的面積計算入手,自主探索推導出平行四邊形面積的計算方法。推導過程中,學生發現可以通過剪切、拼接或者轉化等數學方法,先將平行四邊形剪出一個直角三角形,再向右平移拼成一個長方形;還有學生發現,可以沿著平行四邊形任意一條高剪出一個直角三角形,并將其向右平移,拼成一個長方形。學生比較兩種方法后得出結論:根據拼接前后兩個圖形的面積不變這個現象,可以知道平行四邊形面積等于長方形的面積,而且長方形的長等于原來平行四邊形的底,長方形的寬就是原來平行四邊形的高。根據這個關系繼續推理,學生很快根據長方形的面積為“長×寬”,推導出平行四邊形的面積為“底×高”。這兩者之間有什么關系呢?為了清晰呈現整個推理邏輯,讓學生一目了然地看到面積推理的全過程,筆者運用思維導圖呈現推導過程,如圖2所示。
以上思維導圖將拼接、平移、轉化的過程清晰地呈現出來。學生借助它在頭腦中建立起長方形和平行四邊形面積的本質關聯,還為下一步繼續學習三角形面積、梯形面積等積累了經驗。
三、強化擴展設計,把握疑難要素
學習的過程是一個不斷分析問題、解決問題的過程。教師可以通過思維導圖,直觀呈現數學條件之間的關系,引導學生進行數學猜想,從而找到關鍵元素,深入理解數學所學知識。
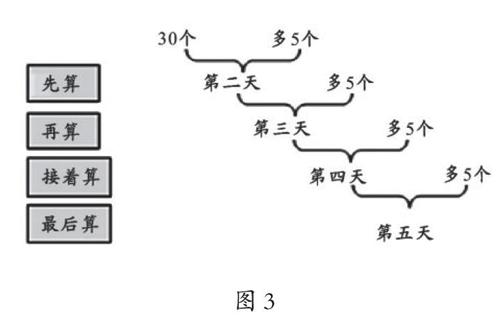
部編版教材三年級上冊《解決問題的策略》中有這樣一個數學表達:“以后每天都比前一天多摘5個。”教學中,不少學生難以準確理解這句話表達的意思。為了解決這個疑惑,筆者運用思維導圖(如圖3),向學生直觀呈現整個探究過程——讓學生思考:假設第一天是30個,第二天是多少個?假設第二天是35個,第三天是多少個?假設第三天是40個,第四天是多少個?假設第五天是35個,能求出第6天多少個嗎?
學生根據思維導圖,由上而下循著條件和問題之間的關系,找準了兩個關鍵元素,從而實現了條件和問題的有效對接,讓疑難問題得到解決。
四、整合知識結構,構建認知系統
運用思維導圖能夠將學生平時習得的零散的知識加以整理和歸納,幫助學生獲得探索數學知識的策略,有效提升數學思維。
部編版五年級下冊《因數和倍數的整理與練習》的知識點比較繁雜,需要對所學的有關倍數、因數、質數、合數等相關知識歸納整理。為了讓學生對所學的知識有清晰地把握,筆者設計了如圖4所示的思維導圖。
通過以上思維導圖,學生把握住了質數、合數、因數、倍數等已學知識的內涵,并從橫向和縱向兩個方面貫通了因數和倍數之間的復雜關系,建構起系統化的知識體系。
(作者單位:襄陽市松鶴路小學)

