最大風速的估算方法與應用

孫 超，湯 超，韓俊杰

（1.黑龍江省太平國際機場氣象臺，黑龍江 哈爾濱 150001；2.黑龍江省氣象科學研究所，黑龍江 哈爾濱150030）

1 引言

風速是指空氣質點在單位時間內所移動的水平距離，以m/s 為單位，精度為一位小數。最大風速是指一段時間內出現的最大10 min 平均風速極大值。 極大風速（陣風）是指某個時間段內出現的最大瞬時風速值[1]。 依據《建筑結構荷載規范》中的《全國基本風壓分布圖》 的風壓和運行維護經驗估算不同重現期水平的線路基本風壓和最大風速是目前國內建筑規劃設計施工和電力設計施工單位獲取最大設計風速的主要方法。 但是由于以前氣象資料站點少，而且沒有考慮地形影響，在地形相對復雜、受臺風影響頻繁的東南沿海地區， 應用這種方法則往往會出現較大偏差。

為此， 在沿海和山地地區最大風速的獲取方法與技術方面國內外相關部門單位已經進行了大量研究，并取得了很多成就。 如龐文保、李懷川[2]等人應用經驗頻率法和P-Ⅲ型分布分析獲得15 m 高度的15 a 一遇的最大風速。 莊垂鋒[3]曾經利用福州氣象站的1953-1982 年的最大風速觀測資料分析過福州的最大風速時空分布特征，用極值Ⅰ型分布(即Gumbel 分布) 理論估算福州市不同重現期內可能的最大風速值。 龐文保、白光弼等[4]應用皮爾遜Ⅲ型和極值Ⅰ型分布曲線對陜西省乾縣和扶風兩個氣象站1972-2004 年10 min 平均最大風速資料進行30 a 一遇和50 a 一遇自記10 min 平均最大風速進行極值推斷，認為兩種方法用于電力部門所需最大風速估算都是可行的。

但是以上這些分析研究都是以地面氣象站的實際觀測資料為基礎展開的。 由于地區內不同氣象站的建站早晚以及開始自記風速風向觀測的時間不同，開始階段通常是以每日4 次或3 次定時2 min 平均風速觀測記錄， 即使在觀測氣象站有自記風速風向觀測記錄， 有些年份也存在缺測現象或者因觀測站搬遷而受到影響。 因觀測高度不同和時次差異須進行相應訂正。 訂正模式的系統誤差以及不可避免的偶然誤差都會對計算結果的準確性產生影響。

廣東地區處于我國華南南部沿海地區， 地形復雜且易受臺風等惡劣天氣影響導致大風等災害。 劉少群，黃澤文，陳麗佳等人曾對廣東省的風災狀況展開過調查， 認為導致廣東地區風災的主要原因有熱帶氣旋以及中尺度強對流中的颮線與龍卷， 并給出了相應的風災防范治理意見[5]。 但目前對該地區的最大風速分布特征以及其極值估算的相關研究分析還較少。 本文使用ECMWF 的REA 分層格點資料對廣東及其近海地區風速分布情況進行描述， 統計獲得該地區地面以及近地層不同高度上最大平均風速分布特征， 應用皮爾遜Ⅲ型和極值Ⅰ型分布得到本地10 a、20 a、50 a 一遇的最大風速極值，為以后本地的氣候狀況研究和當地建設規劃提供參考。

本文中主要通過對數據的統計分析，總結（18°-26.5°N,108.75°-118.5°E） 地區的不同高度風場的時空分布特征。

應用極值Ⅰ型分布和皮爾遜Ⅲ型曲線兩種方法對ECMWF 的多層風場REA 數據資料的不同高度層的年最大風速序列展開分析，并獲得各層10 a、20 a、50 a 不同重現水平下的最大風速估計值， 并與初始資料加以比較分析， 總結了這兩種方法在實際生產中的應用價值。

2 數據與方法

2.1 數據

初始風速資料是源自ECMWF 的空間分辨率為0.75°×0.75°的 REA 多層 10 min 平均風速格點資料。所取用資料空間為 18°-26.25°N，108.75°-118.5°E 區域，基本覆蓋廣東省全境以及附近近海地區。 資料為從 1979-2012 年共 34 a 每天 4 個時次的 10 min 平均風速, 再分析資料中距地面高度分別為10 m、30 m、60 m、100 m 四層的平均風速數據，可較好的代表東南沿海地區的最大風速特征。

2.2 研究方法

本文中主要通過對數據的統計分析，總結（18°-26.5°N,108.75°-118.5°E） 地區的不同高度風場的時空分布特征。

應用極值Ⅰ型分布和皮爾遜Ⅲ型曲線兩種方法對ECMWF 的多層風場REA 數據資料的不同高度層的年最大風速序列展開分析，并獲得各層10 a、20 a、50 a、不同重現水平下的最大風速估值，并與初始資料加以比較分析， 總結了這兩種方法在實際生產中的應用價值。

3 不同高度最大風速分布特征分析

3.1 歷史最大風速分布特征

文中所研究的區域為華南南部地區， 以及其毗鄰的近海海域，空間分辨率為0.75°×0.75°，所占總面積大約8×105km2。 其中陸地主要包括廣東省全部和附近的廣西東北部、湖南南部、江西南部、福建省西南部以及海南島。

在研究區域，根據現有資料分別對100 m、60 m、30 m、10 m 四個高度按格點統計獲取全風速的最大值， 并繪制了不同高度層1979-2012 年年最大風速變化曲線如下（圖1）。

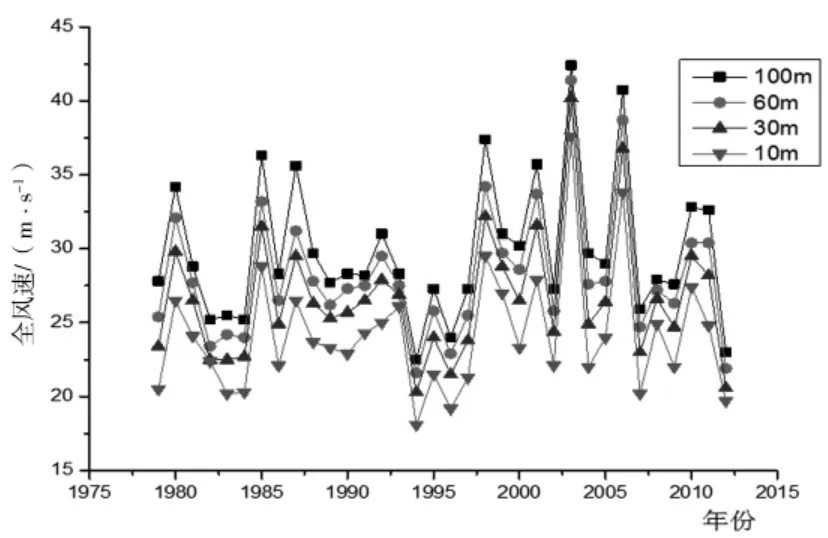
圖1 各層年最大風速年紀變化曲線

在研究區域(18°-26.25°N，108.75°-118.5°E)內年最大全風速值從高到低逐漸減小。100 m 高度層的年際差異在22.5-42.5 m/s 之間， 平均年最大風速為29.8 m/s；60 m 高度層的年際差異在 21.6-41.4 m/s之間，平均年最大風速為28.0 m/s；30 m 高度層的年際差異在20.3-40.2 m/s 間， 平均年最大風速為26.6 m/s；10 m 高度層的年際差異在18.1-37.6 m/s 之間，平均年最大風速為24.2 m/s。其中年最大風速的年際極大值出現在2003 年，次大值出現在2006 年；年際極小值出現在1994 年，次小值出現在1996 年。

由圖1 可見，在所研究范圍內，全風速的年最大值的空間極值有著非常明顯的年際變化， 不同高度層的變化趨勢十分吻合。 所統計歷史范圍內，年最大風速的極大值出現在2003 年， 次大值出現在2006年，極小值出現在1994 年。 從曲線的波動情況來看,自2000 年以來曲線波動相對增強，即出現的極大值有所增大。 這充分說明了年最大風速的不確定的特點， 因而需要通過科學的統計以獲得在一定時間范圍內一遇的可能最大風速。

研究區域內各層最大全風速的極大值均出現在近海的海上， 極小值一般出現在粵北或粵東北的山地地區。 在研究區域內的各個高度層上歷史最大全風速有明顯的較差（最大值和最小值之差），較差值一般在10-12 m/s 之間。沿海海岸線附近由于下墊面性質的突然變化， 下墊面粗糙度增大， 摩擦作用變強。 風速的梯度最大，從海上到陸地風速迅速減小，從海岸到內陸的狹窄地帶內風速能夠迅速減小4-6 m/s。從海岸附近的平原和臺地向內陸的山區延伸，各層風速也因下墊面性質的改變而減弱。 在近海、沿海岸線以及內陸山區，最大風速有著不同的分布特點。在100 m 高度層上最大風速的極大值與極小值的較差為12 m/s，其中極大值出現在海上，極小值出現在粵北的山區， 而且在海岸線附近風速等值線走向與海岸線相吻合。 在 60 m、30 m、10 m 三個高度層上也有類似的分布特征。

由研究區域歷史的年最大風速分布狀況， 可將研究區域按照近海、沿海岸線、內陸山地劃分為三類區域。 在每類區域內選取兩個代表點對其最大風速的分布特征加以分析，并估算該點上的最大風速值。在近海類區域中選擇 A （21°N,112.5°E） 和 B (21°N,115.5°E) 為代表點， 在沿海岸線類區域中選擇C（21.75°N,111.75°E）和 D（22.5°N,113.25°E）為代表點，在內陸山地類區域中選擇 E（24°N，112.°5E）和 F(24°N,115.5°E)為代表點。

3.2 代表點最大風速年內分布特征

為確定年最大風速出現的季節， 須對各代表格點月最大風速的變化趨勢進行統計分析。 根據氣候統計學的統計規律， 一般在30 a 周期內某地的氣候條件一般不會有明顯的變化， 所以選擇最近1 a，即2012 年各代表格點的月最大風速資料為代表考察研究區域月最大風速的變化規律。

分別對六個代表格點 A、B、C、D、E、F 處 2012 年的月最大風速變化情況統計如下圖2：

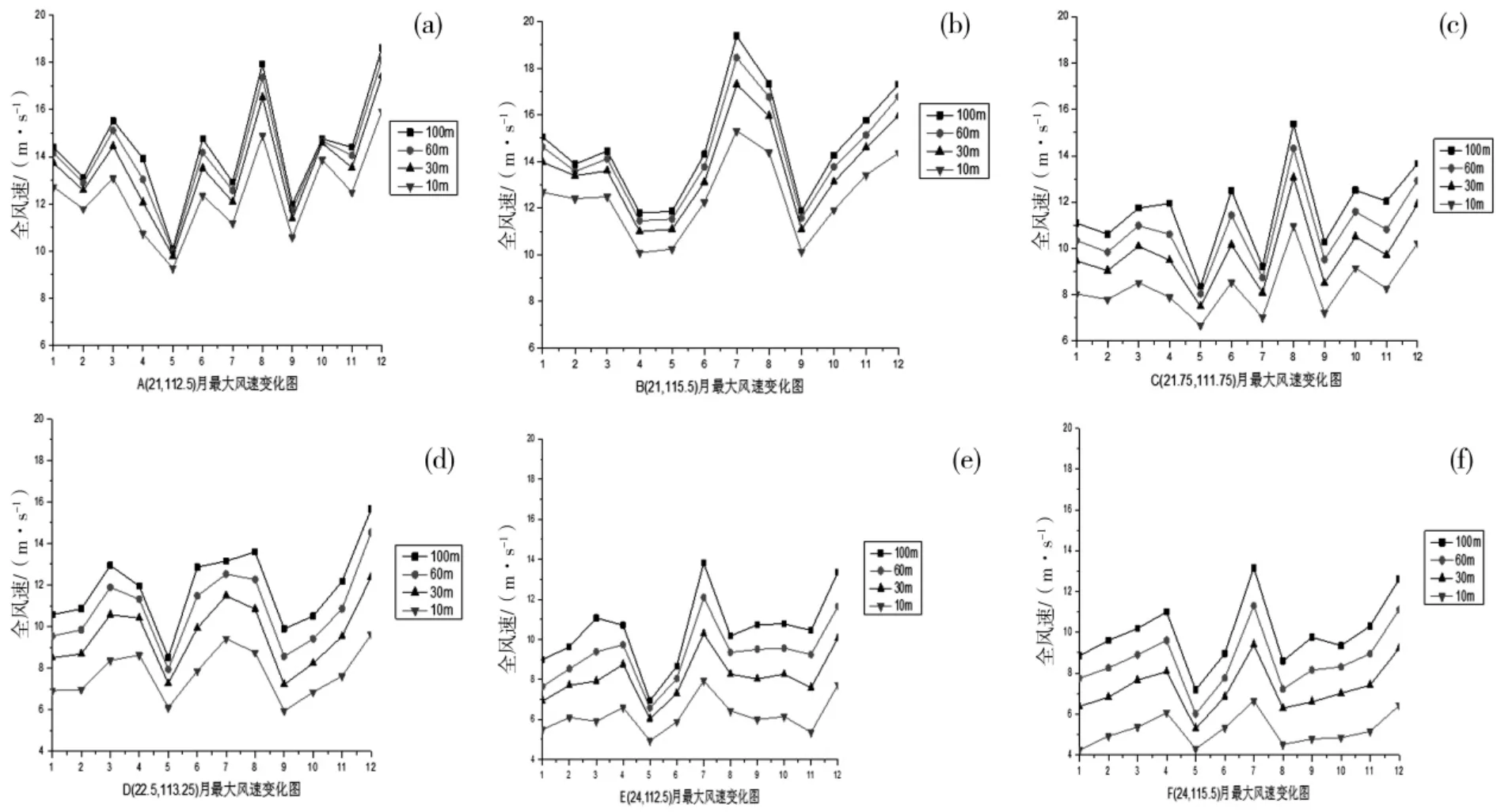
圖2 (a)A、(b)B、(c)C、(d)D、(e)E、(f)F 六點 2012 年月最大風速變化

分別分析以上各點月最大風速變化情況可見，在近海類區域代表格點A、B， 其月最大風速的極大值一般出現在7 月或者8 月； 在沿海岸線類區域代表格點C， 其月最大風速極大值一般出現在6、7、8月，即氣候意義上的夏季，而D 點月最大風速的極大值出現在12 月份，次大值出現8 月；在內陸山地類區域代表格點E、F，其月最大風速極大值也是出現在7、8 月份， 但相對近海類域其極大值并無明顯突變。在所有格點上， 月最大風速的極小值都出現在5 月份、9 月份和10 月份，這與太陽直射點的南北移動而使西太平洋副熱帶高壓控制本地有著必然關系。 夏季的7、8 月份， 是西太平洋副熱帶高壓最靠北的時間，這段時間研究區域位于副熱帶高壓后部，經常會受到來自菲律賓以東太平洋和中國南海溫暖洋面上的熱帶氣旋甚至臺風的影響。

比較各圖可見， 在近海類區域月最大風速的變化情況極為明顯，夏季和冬季有明顯的突變。 而在沿海岸線類區域次之， 并以內陸山地區域的變化最為平穩。 綜合以上月最大風速的分布變化特征，可認為形成研究區域年最大風速值的主要原因是海上的熱帶氣旋及臺風， 但是冬季如果有強的冷空氣翻越南嶺南下也可能形成年最大風速。

4 不同重現期最大風速推算

4.1 極值Ⅰ型分布估算最大風速極值

極值Ⅰ型分布方法是近年來最大風速概率計算以及不同概率下最大風速值極值估算中最常用的方法之一。

根據不同重現水平的概率公式P＝1/R（其中R 為重現水平，以年為單位），可以通過查詢極值Ⅰ型ψp值分布表[6]確定 10 a、20 a、50 a 重現水平下的 ψp 值分別為1.3、1.87、2.59。 這種方法中僅有一個參數ψp與被估計最大風速極值的概率相關， 對于某些特定的概率水平計算方法比較簡單，易于實現。

4.1.1 100 m 層最大風速極值估算

用第Ⅰ型極值分布方法估算各代表研究點100 m 高度不同重現水平下的最大風速可能極值， 得如下結果。

在表1 中可見， 所選取的各代表點100 m 高度上年最大風速序列的變差系數Cv 在0.10-0.20 之間，其中變差系數最大的是代表近海類區域的A 點，值為0.1890， 變差系數最小的是代表內陸山地類區域的E 點，值為0.1072。 在三類區域中，近海類區域、沿海岸線類區域、 內陸山地類區域的變差系數依次減小， 表明從海上到內陸山地區域年最大風速序列的相對變動程度依次減小， 即年最大風速序列從近海到內陸的波動逐步減小。

根據第Ⅰ型極值分布估算得到的研究代表點10 a 重現水平下的最大風速極值介于16-28 m/s 之間，20 a 重現水平下的最大風速極值介于17-29 m/s 之間，50 a 重現水平下的最大風速極值介于18-33 m/s之間。 與1979-2012 年的34 a 年最大風速極大值相比較重現水平為50 a 時估算的最大風速極大值與之比較接近。

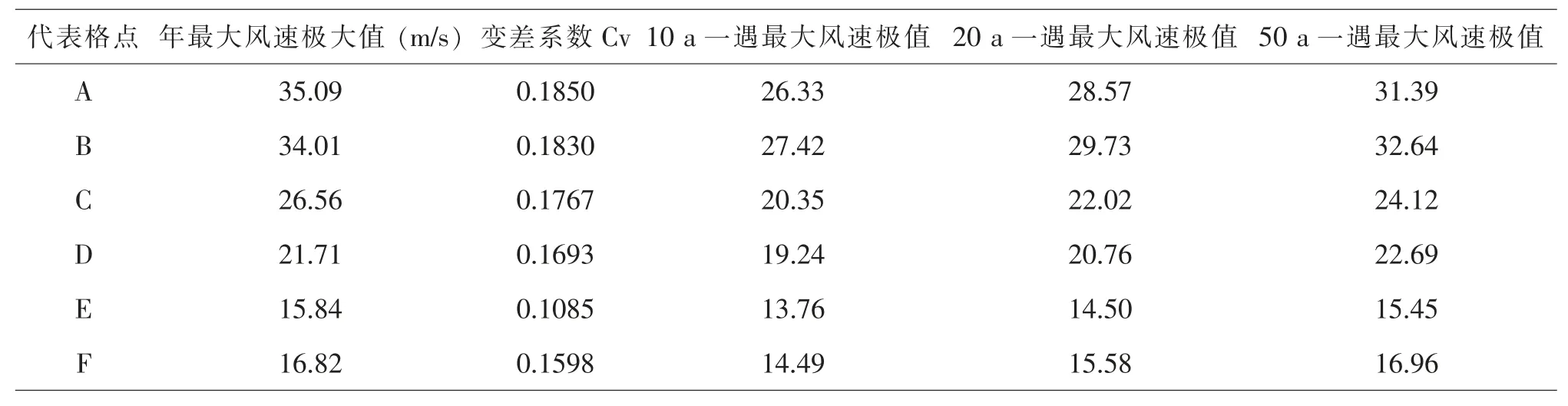
表2 60 m 高度各代表點極值Ⅰ型分布的最大風速極值估計表

4.1.2 60 m 層最大風速極值估算

用第Ⅰ型極值分布方法估算各代表研究點60 m高度不同重現水平下的最大風速可能極值， 得如下結果。

在表2 中可見，對所選取研究代表點A、B、C、D、E、F 各點60 m 高度年最大風速序列的變差系數與100 m 高度基本一致。10 a 重現水平下的最大風速極值介于14-27 m/s 之間，20 a 重現水平下的最大風速極值介于15-29 m/s 之間，50 a 重現水平下的最大風速極值介于16-32 m/s 之間。所計算各重現期水平下的年最大風速的估算極值相對實際資料統計的年最大風速極大值偏小。

4.1.3 30 m 層最大風速極值估算

用第Ⅰ型極值分布方法估算各代表研究點30 m高度不同重現水平下的最大風速可能極值， 得如下結果。

在表3 中可見，對所選取研究代表點A、B、C、D、E、F 各點30 m 高度10 a 重現水平下的最大風速極值介于12-25 m/s 之間，20 a 重現水平下的最大風速極值介于13-27 m/s 之間，50 a 重現水平下的最大風速極值介于14-30 m/s 之間。所計算各重現期水平下的年最大風速的估算極值相對實際資料統計的年最大風速極大值偏小。

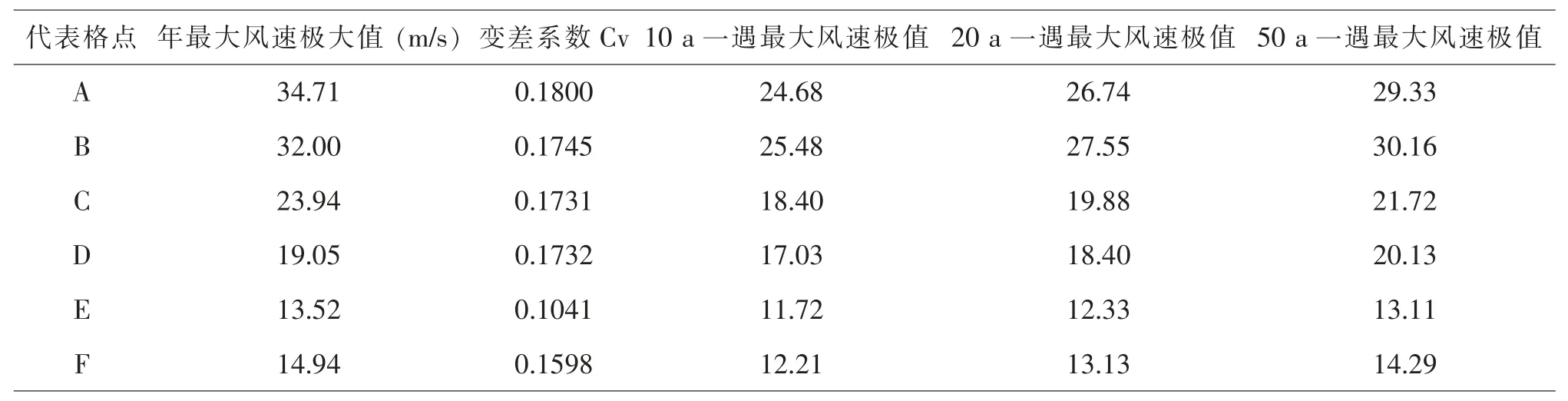
表3 30 m 高度各代表點極值Ⅰ型分布的最大風速極值估計表

4.1.4 10 m 層最大風速極值估算

用第Ⅰ型極值分布方法估算各代表研究點10 m高度不同重現水平下的最大風速可能極值， 得如下結果。

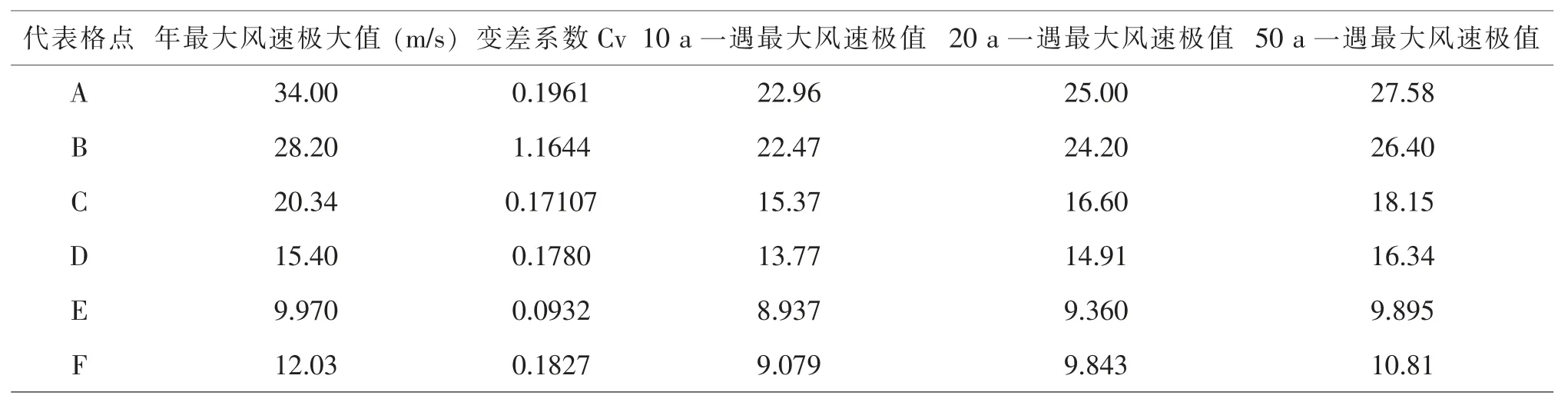
表4 10 m 高度各代表點極值Ⅰ型分布的最大風速極值估計表

在表4 中可見，對所選取研究代表點A、B、C、D、E、F 各點10 m 高度10 a 重現水平下的最大風速極值介于9-23 m/s 之間，20 a 重現水平下的最大風速極值介于9-25 m/s 之間，50 a 重現水平下的最大風速極值介于10-28 m/s 之間。所計算各重現期水平下的年最大風速的估算極值相對實際資料統計的年最大風速極大值偏小。

4.2 皮爾遜Ⅲ型分布估算最大風速極值

最大風速極值作為氣候隨機變量在數學意義上是不穩定的,但它隨時間變化過程在概率上卻是穩定的。 最大風速這一氣象要素在概率上的分布特征暫時還沒有確定。 上文已經利用正態分布的極值Ⅰ型分布這一正態分布模型， 對其隨時間變化的概率特征進行了一定分析。 現選用皮爾遜Ⅲ型這一偏態分布模型對其隨時間變化的概率分布特征加以分析，并比較兩種不同分布模型的特征分析結果， 總結不同分布模型下隨時間變化的概率分布特征的異同。同時， 皮爾遜Ⅲ型分布在我國電力部門工程設計的最大風速估計和水文單位洪量分析估計中有著廣泛的應用， 是極值估計中應用極為普遍的一種統計分布方法。

4.2.1 100 m 層最大風速極值估算

用皮爾遜Ⅲ型分布方法估算各代表研究點100 m 高度不同重現水平下的最大風速可能極值， 得結果如下表：

在表5 中可見， 根據皮爾遜Ⅲ分布估算得到的研究代表點100 m 高度層10 a 重現水平下的最大風速極值介于16-28 m/s 之間，20 a 重現水平下的最大風速極值介于17-31 m/s 之間，50 a 重現水平下的最大風速極值介于18-34 m/s 之間。與1979-2012 年的34 a 年最大風速序列的極大值相比較， 重現水平為50 a 時估算的最大風速極大值與之比較接近。 但是在近海類區域和沿海岸線類區域中， 估算的極大值相比實際風速序列小2 m/s 左右。

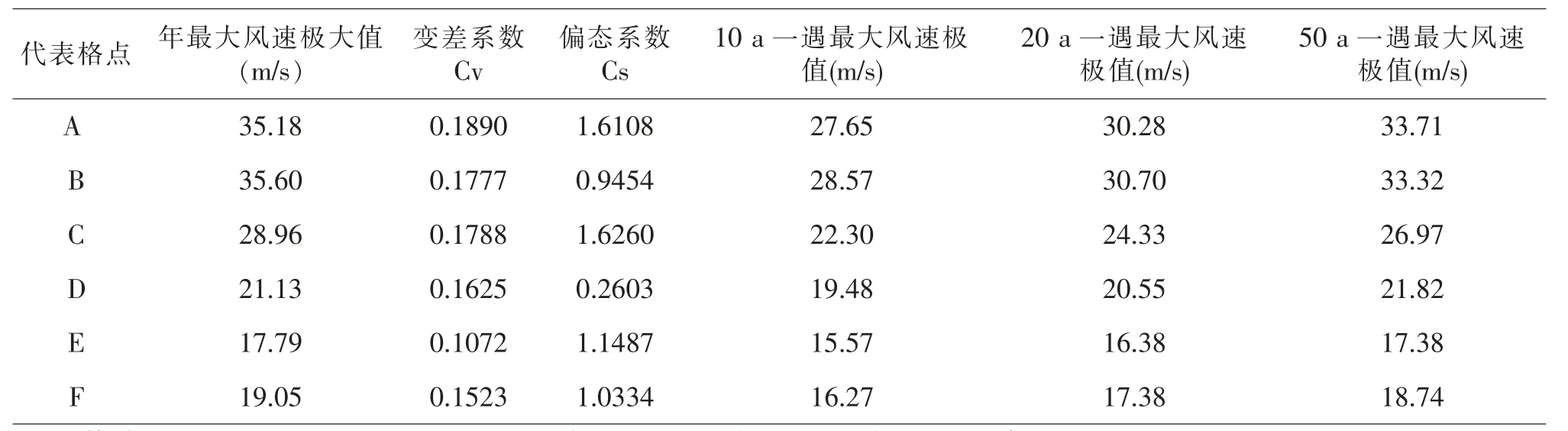
表5 100 m 高度各代表點P-Ⅲ型分布的最大風速極值估計表

4.2.2 60 m 層最大風速極值估算

用皮爾遜Ⅲ型分布方法估算各代表研究點60 m高度不同重現水平下的最大風速可能極值， 得結果如表6：

在表6 中可見，對所選取研究代表點A、B、C、D、E、F 各點60 m 高度年最大風速序列的變差系數與100 m 高度基本一致。10 a 重現水平下的最大風速極值介于14-27 m/s 之間，20 a 重現水平下的最大風速極值介于15-29 m/s 之間，50 a 重現水平下的最大風速極值介于16-33 m/s 之間。所計算各重現期水平下的年最大風速的估算極值相對實際資料統計的年最大風速極大值偏小。

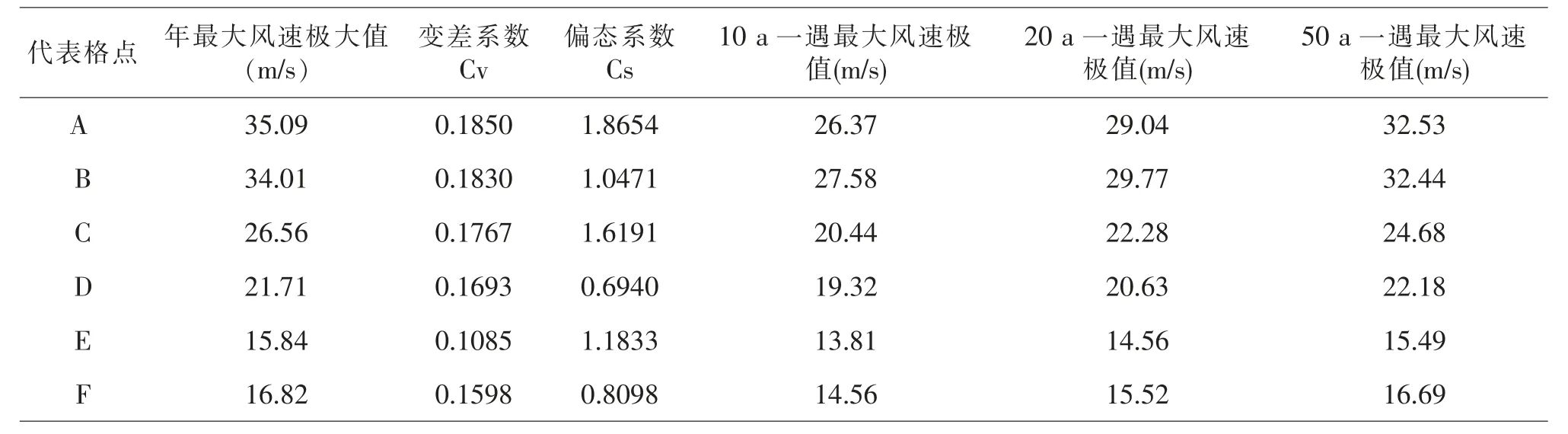
表6 60 m 高度各代表點P-Ⅲ型分布的最大風速極值估計表

4.2.3 30 m 層最大風速極值估算

用皮爾遜Ⅲ型分布方法估算各代表研究點30 m高度不同重現水平下的最大風速可能極值， 得結果如下表：

在表7 中可見，對所選取研究代表點A、B、C、D、E、F 各點30 m 高度年最大風速序列的變差系數與100 m 高度也基本一致。10 a 重現水平下的最大風速極值介于12-25 m/s 之間，20 a 重現水平下的最大風速極值介于14-28 m/s 之間，50 a 重現水平下的最大風速極值介于15-32 m/s 之間。所計算各重現期水平下的年最大風速的估算極值相對實際資料統計的年最大風速極大值偏小。

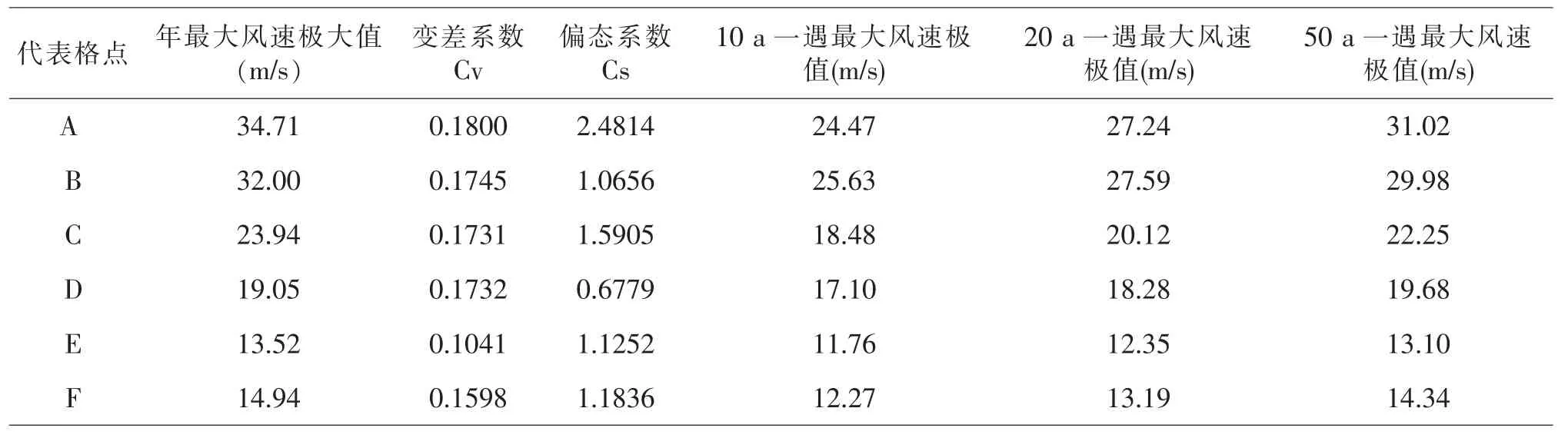
表7 30 m 高度各代表點P-Ⅲ型分布的最大風速極值估計表

4.2.4 10 m 層最大風速極值估算

用皮爾遜Ⅲ型分布方法估算各代表研究點10 m高度不同重現水平下的最大風速可能極值， 得結果如表8：

在表8 中可見，對所選取研究代表點A、B、C、D、E、F 各點10 m 高度年最大風速序列的變差系數與100 m 高度也基本一致。10 a 重現水平下的最大風速極值介于9-23 m/s 之間，20 a 重現水平下的最大風速極值介于9-26 m/s 之間，50 a 重現水平下的最大風速極值介于12-30 m/s 之間。所計算各重現期水平下的年最大風速的估算極值相對實際資料統計的年最大風速極大值偏小。

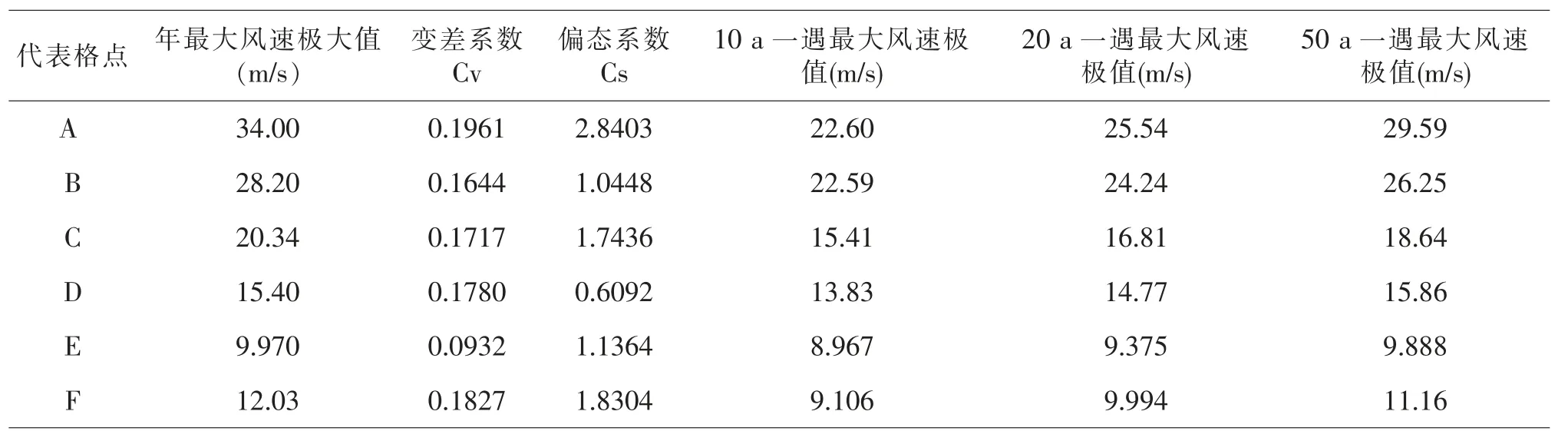
表8 10 m 高度各代表點P-Ⅲ型分布的最大風速極值估計表

4.3 最大風速估算結果的比較

第Ⅰ型極值分布是一種正態分布模型， 皮爾遜Ⅲ型分布是一種偏態分布模型， 兩種模型都常用于不同概率水平下某些氣象要素極值以及其他要素極值的估算。 兩種分布模型因其分布函數與圖線不同，故其分布結果也會有差異。

上文中分別利用兩種方法對研究區域內六個代表點不同高度層上不同重現期水平， 即不同概率水平下的極大值予以估算。 現就其不同估算結果加以對比分析。

4.3.1 100 m 層最大風速極值估算比較

在100 m 高度層上其最大風速估算結果對比，如下：

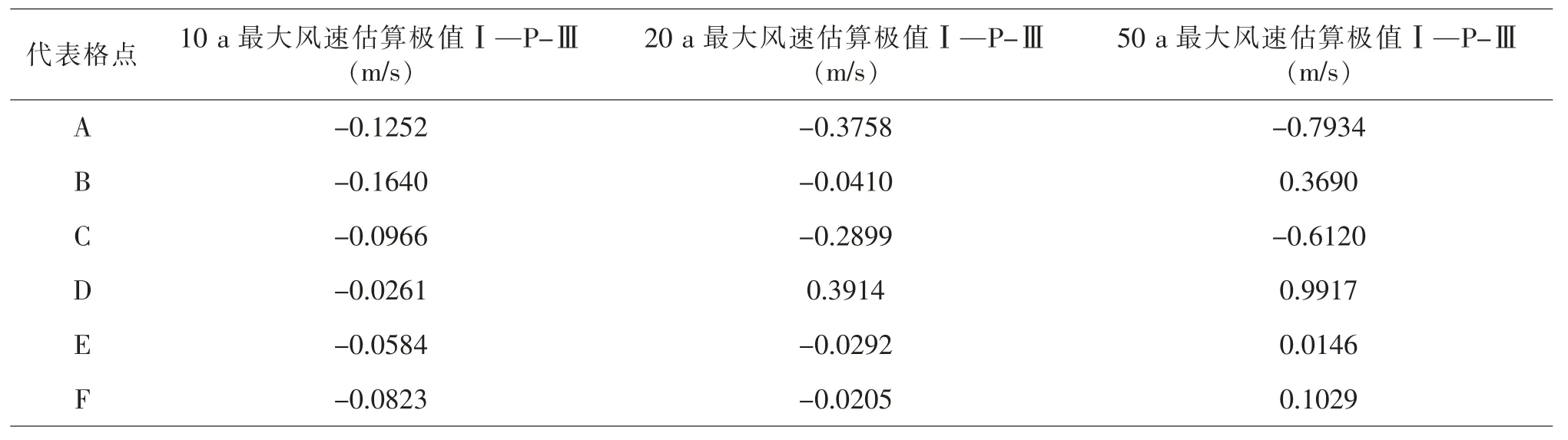
表9 100 m 層極值Ⅰ型與P-Ⅲ型最大估算風速差值

根據表9 中統計數據可見， 兩種方法在100 m高度層的最大風速估算應用中， 它們的估算結果有些差異。在重現水平為10 a 條件下，對同一樣本的估算中皮爾遜Ⅲ型分布的估算結果要略大于用第Ⅰ型極值分布估算的結果；重現水平為20 a 條件下，大部分統計代表點的估算結果仍是皮爾遜Ⅲ型分布的估算結果要略大于用第Ⅰ型極值分布估算的結果，但在沿海岸線類區域的代表點D 極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型分布的估算結果； 重現水平為50 a 條件下的估算結果與重現期水平較短的10 a、20 a 結果則相反， 大部分研究代表點的估算結果為第Ⅰ型極值分布的估算值大于皮爾遜Ⅲ型分布的估算結果， 僅有代表近海類區域的A 點和代表沿海岸線類區域的C 點估算結果為第Ⅰ型極值分布的估算值小于皮爾遜Ⅲ型分布的估算結果。

分別對兩種方法在近海類區域、 沿海岸線類區域、 內陸山地類區域10 a 重現期水平的估算結果對比， 可見在近海類區域中兩種方法的估算結果差值的絕對值最大，沿海岸線類區域與近海類區域類似，內陸山地類區域最小，而重現期水平較長的20 a、50 a 估算結果的差值沒有明顯的變化規律。比較各類區域不同重現期水平的差值結果， 具有重現期越長差值的絕對值越大的特點， 其中以近海類區域代表點A、B 處最為明顯。

4.3.2 60 m 層最大風速極值估算比較

在表10 中可見， 兩種方法應用在60 m 高度層的最大風速估算結果有如下差異， 在重現水平為10 a 條件下，對同一樣本的估算中皮爾遜Ⅲ型分布的估算結果要略大于用第Ⅰ型極值分布估算的結果；重現水平為20 a 條件下大部分統計代表點的估算結果仍是皮爾遜Ⅲ型分布的估算結果要略大于用第Ⅰ型極值分布估算的結果， 但在沿海岸線類區域的代表點D、F 極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型分布的估算結果； 重現水平為50 a 條件下兩種方法的估算結果各有大小， 其差值在近海類區域的代表點處最大，沿海岸線類區域代表點處次之，以內陸山地類區域代表點處為最小。

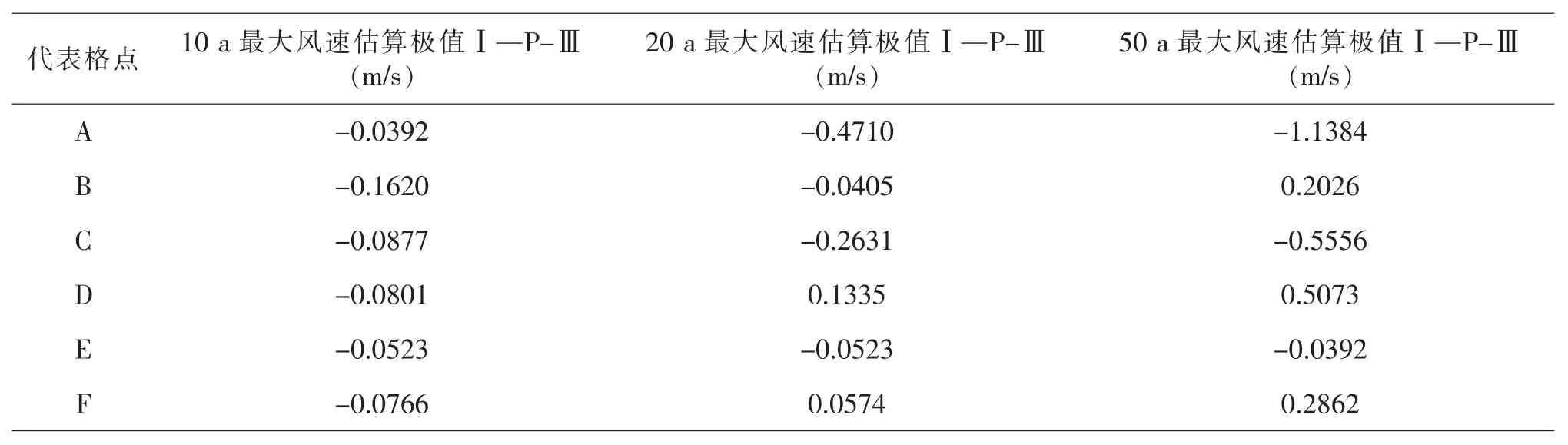
表10 60 m 層極值Ⅰ型與P-Ⅲ型最大估算風速差值

但在此高度層上， 同類區域不同重現期水平條件下的差異并無明顯規律。在A 點隨重現期變長，皮爾遜Ⅲ型分布的估算結果比第Ⅰ型極值分布估算的結果大的差值不斷增大，而在B 點則有相反的規律，隨重現期變長極值Ⅰ型估算結果相對變大， 而且在重現期為50 a 時超過皮爾遜Ⅲ型分布的估算結果。在相同的重現期水平下， 以內陸山地類區域兩種方法的估算結果差值最小。

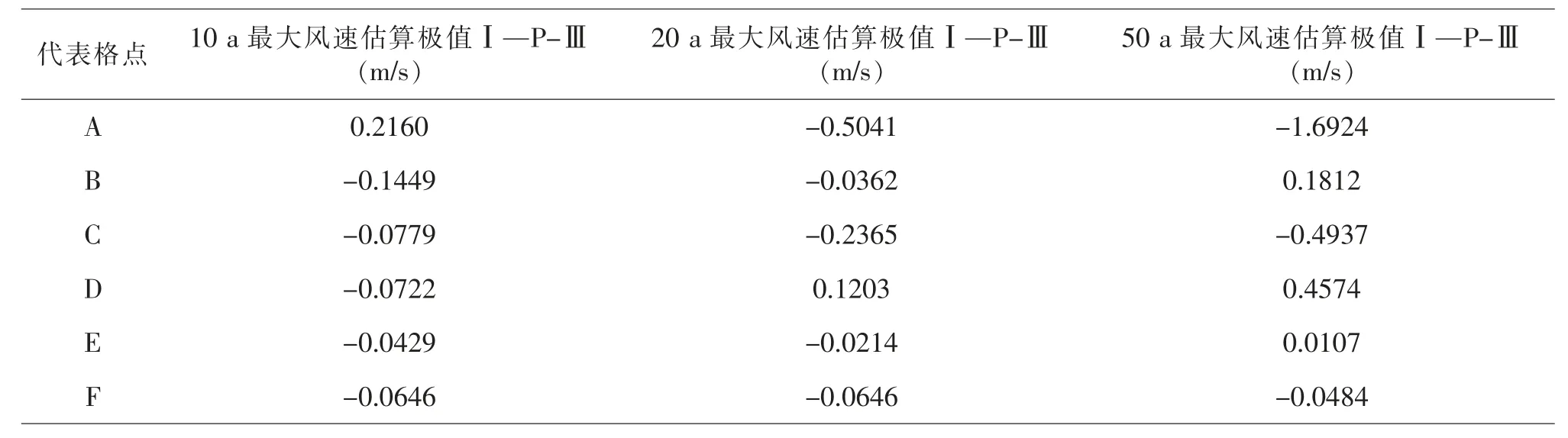
表11 極值Ⅰ型與P-Ⅲ型最大估算風速差值

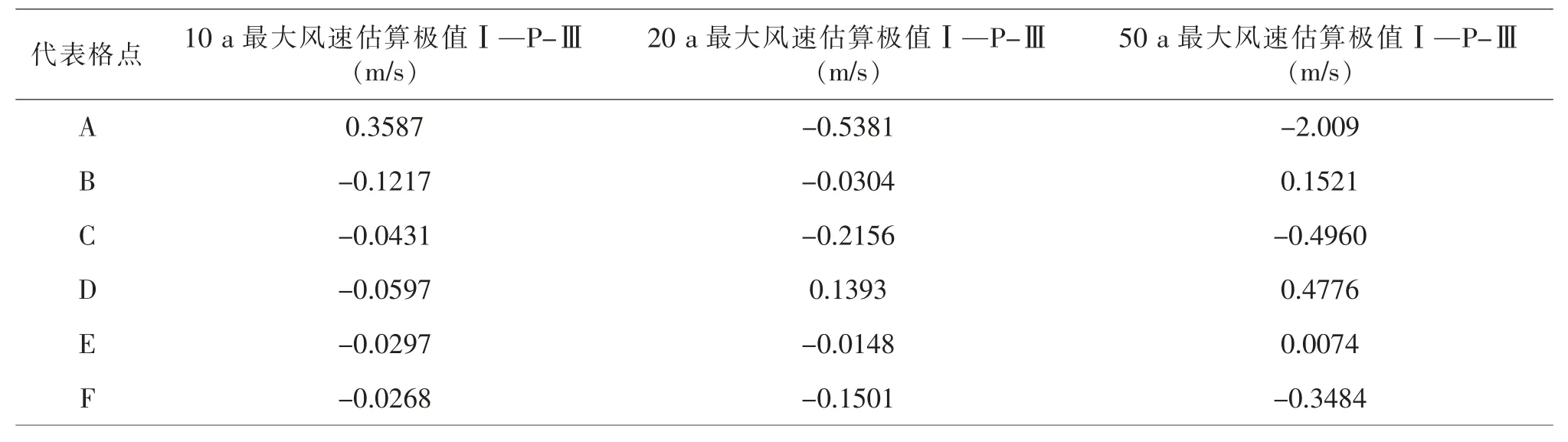
表12 10 m 層極值Ⅰ型與P-Ⅲ型最大估算風速差值

4.3.3 30 m 層最大風速極值估算比較

在表11 中可見， 兩種方法應用在30 m 高度層的最大風速估算結果有如下差異： 在10 a 重現期水平條件下， 極值Ⅰ型分布估算的最大風速結果與皮爾遜Ⅲ型分布估算的最大風速結果相比較偏小，僅在A 點極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型的估算結果；在20 a 重現期水平條件下，極值Ⅰ型分布估算的最大風速結果與皮爾遜Ⅲ型分布估算的最大風速結果相比較偏小， 僅在D 點極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型的估算結果； 在50 a 重現期水平條件下， 在A、C、F 三點極值Ⅰ型分布的估算結果小于皮爾遜Ⅲ型分布的估算結果， 在B、D、E 三點極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型分布的估算結果。

4.3.4 10 m 層最大風速極值估算比較

在表12 中可見， 兩種方法應用在10 m 高度層的最大風速估算結果有如下差異： 在10 a 重現期水平條件下極值Ⅰ型分布估算的最大風速結果與皮爾遜Ⅲ型分布估算的最大風速結果相比較偏小， 僅在A 點極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型的估算結果； 在20 a 重現期水平條件下極值Ⅰ型分布估算的最大風速結果與皮爾遜Ⅲ型分布估算的最大風速結果相比較偏小， 僅在D 點極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型的估算結果； 在50 a 重現期水平條件下， 在A、C、F 三點極值Ⅰ型分布的估算結果小于皮爾遜Ⅲ型分布的估算結果， 在B、D、E 三點極值Ⅰ型分布的估算結果大于皮爾遜Ⅲ型分布的估算結果。

4.3.5 比較結果分析

綜合以上對第Ⅰ型極值分布和皮爾遜Ⅲ型分布在各個高度層上差值分布特征的分析可見， 當所取重現期水平較短時極值Ⅰ型分布的估算結果往往大于皮爾遜Ⅲ型分布的估算結果， 所取重現期水平較長時其估算結果差異無明顯規律，須具體比較。

在100 m 高度層上兩種分布方法所得估算結果的最大差值的絕對值為D 點50 a 重現期水平的差值0.99 m/s，其對極值Ⅰ型分布估算結果的相對差值為4.3%， 對皮爾遜Ⅲ型分布估算結果的相對差值為4.5%；在60 m 高度層上兩種分布方法所得估算結果的最大差值的絕對值為A 點50 a 重現期水平的差值1.14 m/s，其對極值Ⅰ型分布估算結果的相對差值為3.6%， 對皮爾遜Ⅲ型分布估算結果的相對差值為3.5%；在30 m 高度層上兩種分布方法所得估算結果的最大差值的絕對值為A 點50 a 重現期水平的差值1.69 m/s，其對極值Ⅰ型分布估算結果的相對差值為5.7%， 對皮爾遜Ⅲ型分布估算結果的相對差值為5.4%；在10 m 高度層上兩種分布方法所得估算結果的最大差值的絕對值為A 點50 a 重現期水平的差值2.0 m/s， 其對極值Ⅰ型分布估算結果的相對差值為7.2%， 對皮爾遜Ⅲ型分布估算結果的相對差值為6.7%。 所以，兩種方法估算結果的差值對于其估算結果而言偏差較小， 特別是內陸山地類區域其相對差值更小，幾乎可予以忽略。 所以，兩種方法都可應用于最大風速估算。

5 結論

本文通過分析ECMWF 的1979-2012 年的空間分辨率為 0.75°×0.75°的REA 每日四個時次的多層10 min 平均風速格點資料， 提取了研究區域 (18°-26.25°N，108.75°-118.5°E) 空間內的年最大風速序列， 并對其年際變化特征和空間分布特征進行了分析。 在對其空間分布特征進行分析總結的基礎上，把研究區域劃分為不同類別的次研究區域， 分區選擇代表格點統計其年最大風速序列。 分別利用第Ⅰ型極值分布和皮爾遜Ⅲ型分布方法估算了各個代表性格點在不同重現期水平下的最大風速極值， 并比較兩種方法估算結果的異同， 分別繪制了最大風速極值分布圖。 得主要結論如下：

在研究區域內各個不同高度層上其年最大風速序列的年際變化趨勢極為吻合， 最近10 a 以來出現極大風速的頻率增加。 100 m、60 m、30 m、10 m 各層年最大風速平均值之差值一般在1-2 m/s 之間。從空間分布來看，因下墊面性質差異，從近海區域、沿海岸線區域到內陸山地區域，最大風速極值依次減小。

以2012 年為代表統計分析了各代表點月最大風速的變化特征與氣候成因， 認為年最大風速一般是受熱帶氣旋或臺風影響而在夏季形成， 但若是冬季有強的冷空氣能夠翻越南嶺， 在下坡地形作用下也可能出現年最大風速。

第Ⅰ型極值分布是一種正態分布的理論分布。應用第Ⅰ型極值分布估算各個代表格點不同重現水平下年最大風速的極大值隨重現期變長而增大，但重現期水平為10 a、20 a、50 a 所估算極大值較年最大風速統計序列中的極大值偏小。

皮爾遜Ⅲ型分布是一種偏態分布的理論分布。應用皮爾遜Ⅲ型分布估算各個代表格點不同重現水平下年最大風速的極大值與應用第Ⅰ型極值分布估算的結果類似。

對比兩種不同的分布方法估算最大風速極值的原理與結果。 第Ⅰ型極值分布估算中僅可調整一個參數，即變差系數Cv，在皮爾遜Ⅲ型分布估算中則可以同時調整變差系數Cv 與偏態系數Cs，以更加準確的描述最大風的分布情況， 求得更為準確的最大風速估計值。 兩種分布方式在應用原統計樣本所得參數進行最大風速極值估算結果比較表明， 在重現期較短時第Ⅰ型極值分布估算所得結果相對皮爾遜Ⅲ型分布估算結果較小，在重現期較長時須具體討論。但兩種方法所估算結果差值較估算值可予以忽略，兩種方法均可用于最大風速極值估算， 若能夠對計算過程中的參數進行調整得到擬合程度較高的分布曲線， 則可以直接利用分布曲線獲得任意重現水平下的極值，而不受參數表限制，將能夠更加廣泛的應用于計算機估計極值。

本文是在分析ECMWF 的REA 數據的基礎上進行的， 僅對最大風速序列的年際變化和月際變化特征進行了分析， 通過簡單的分布模式估算了不同重現水平的最大風速極值。 但在分析中沒有考慮風向這一重要因素以及地形等因素對最大風速的影響，也沒有對分布模式的參數進行調整以更準確的擬合最大風速分布。 未來通過對實測資料分析，調整分布模型的參數，可求得更準確的最大風速估算極值。 綜合分析地形等因子對最大風速的影響， 結合風向特征分析可得到更具實用意義的成果。