混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法

陳忠云，張達(dá)敏，辛梓蕓，張繪娟，閆 威

貴州大學(xué) 大數(shù)據(jù)與信息工程學(xué)院，貴陽 550025

1 引言

大自然充滿執(zhí)行不同任務(wù)的社交行為，雖然所有個(gè)體和群體行為的最終目標(biāo)是生存，但生物在群體中進(jìn)行合作和互動(dòng)有以下幾個(gè)原因：狩獵、防御、導(dǎo)航和覓食。多種動(dòng)物和昆蟲的智能群體行為多年來引起了研究者的關(guān)注。計(jì)算機(jī)科學(xué)研究人員將這些群體模型作為解決復(fù)雜現(xiàn)實(shí)世界問題的框架，從而產(chǎn)生了人工智能的一個(gè)分支，通常被稱為群體智能。目前已經(jīng)提出了許多的智能優(yōu)化算法，例如遺傳算法（Genetic Algorithm，GA）[1]、粒子群優(yōu)化算法（Particle Swarm Optimization，PSO）[2]、蝴蝶優(yōu)化算法（Butterfly Optimization Algorithm，BOA）[3]等。這些算法已成功應(yīng)用于各種科學(xué)領(lǐng)域，如過程控制、生物醫(yī)學(xué)信號處理[4]、圖像處理以及許多其他工程設(shè)計(jì)問題[5]。

樽海鞘群算法（Salp Swarm Algorithm，SSA）是2017 年由Mirjalili 等人提出的一種新型啟發(fā)式智能算法[6]。樽海鞘群算法具有結(jié)構(gòu)簡單、參數(shù)少、容易實(shí)現(xiàn)等優(yōu)點(diǎn)，受到國內(nèi)外專家學(xué)者廣泛關(guān)注，已被成功應(yīng)用到多目標(biāo)優(yōu)化和工程設(shè)計(jì)問題[6-7]。雖然樽海鞘群算法在求解大部分優(yōu)化問題時(shí)具有優(yōu)越性，但是與其他群智能算法一樣，仍然存在求解精度低和收斂速度慢等缺陷。文獻(xiàn)[8]將樽海鞘群算法中跟隨者單步位置更新方式改為兩步，分別根據(jù)自適應(yīng)平局移動(dòng)策略和領(lǐng)域最優(yōu)引領(lǐng)策略進(jìn)行更新，之后在引入方向?qū)W習(xí)策略以一定概率對個(gè)體位置進(jìn)行擾動(dòng)，提高種群多樣性，使算法跳出局部最優(yōu)。文獻(xiàn)[9]提出固定慣性權(quán)重，可以加快搜索過程中的收斂速度，并應(yīng)用特征選擇問題。文獻(xiàn)[10]把樽海鞘群算法和混沌理論相結(jié)合提出混沌樽海鞘群算法，在解決特征提取問題時(shí)，能發(fā)現(xiàn)最優(yōu)特征子集，最大程度地提高分類精度，最小化所選特征的數(shù)目。文獻(xiàn)[11]提出基于樽海鞘群算法的無緣時(shí)差定位，利用SSA 解決TDOA（Time Difference of Arrival）定位結(jié)算問題，驗(yàn)證算法在多站時(shí)差定位問題上的有效性與優(yōu)越性。文獻(xiàn)[12]提出基于Tent映射的灰狼優(yōu)化算法，通過混沌映射產(chǎn)生初始種群，增加種群個(gè)體的多樣性。文獻(xiàn)[13]提出自適應(yīng)Tent混沌搜索的蟻獅優(yōu)化算法，自適應(yīng)調(diào)整混沌搜索空間得到最優(yōu)解，改善適應(yīng)度較差個(gè)體，提高種群整體的適應(yīng)度和尋優(yōu)效率。文獻(xiàn)[14]改進(jìn)Tent 映射，具有更優(yōu)越的混沌特性，能更好地實(shí)現(xiàn)混沌尋優(yōu)。文獻(xiàn)[15]選擇精英個(gè)體進(jìn)行反向?qū)W習(xí)，拓展種群的搜索區(qū)域，增強(qiáng)多樣性和加速收斂。文獻(xiàn)[16]提出重心方向?qū)W習(xí)（Centroid Opposition-Based Learning，COBL），以整個(gè)群體重心為參考點(diǎn)計(jì)算反向點(diǎn)，這樣反向點(diǎn)包含了群體搜索經(jīng)驗(yàn)。

受上述文獻(xiàn)的啟發(fā)，本文提出了一種改進(jìn)混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法，以解決標(biāo)準(zhǔn)樽海鞘群算法存在的求解精度不高和收斂速度慢等問題。通過改進(jìn)Tent映射來生成樽海鞘群算法的初始種群，增強(qiáng)初始個(gè)體的均勻性。種群個(gè)體更新后，選擇部分精英個(gè)體并采用質(zhì)心拉伸機(jī)制，有利于搜索更多的有效區(qū)域來提高群體的多樣性，增強(qiáng)算法的全局探索和局部開發(fā)能力。通過求解多種維度的12 個(gè)典型復(fù)雜函數(shù)以及部分CEC2014函數(shù)的最優(yōu)解來驗(yàn)證混沌精英質(zhì)心拉伸機(jī)制樽海鞘群算法（Chaotic and Elite centroid stretching mechanism Salp Swarm Algorithm，CESSA）的有效性。

2 樽海鞘群算法

樽海鞘群算法[6]是Mirjalili 等人揭示的一種全新的智能優(yōu)化算法，這種算法的思想出自于樽海鞘的聚集行為，即樽海鞘鏈。樽海鞘以水中的浮游植物（海藻等）為食，通過吸入噴出海水完成在水中的移動(dòng)。在樽海鞘群算法中，樽海鞘鏈由兩種類型的樽海鞘組成：領(lǐng)導(dǎo)者和追隨者。領(lǐng)導(dǎo)者位于樽海鞘鏈的最前面，而其他個(gè)體則為追隨者的角色。

樽海鞘的種群行為與其他算法有所不同，其并不是以“群”分布，而是采用頭尾連接的形式，組成“鏈”的形態(tài)，順次跟隨著移動(dòng)。樽海鞘鏈中的領(lǐng)導(dǎo)者排在隊(duì)伍的最前端，它對環(huán)境有著最優(yōu)的判斷，但與其他群智能算法不同的是，領(lǐng)導(dǎo)者不會(huì)直接影響整個(gè)種群的移動(dòng)方向，而是直接影響緊接著的第二個(gè)樽海鞘個(gè)體的位置更新，第二個(gè)個(gè)體影響第三個(gè)個(gè)體，以此類推。因此，領(lǐng)導(dǎo)者的位置對其余樽海鞘位置影響程度會(huì)順位遞減，這使排在后面的個(gè)體有著更好的多樣性。

在樽海鞘群算法中，定義每個(gè)樽海鞘個(gè)體的位置矢量X用于在N維空間中搜索，其中N是決策變量的數(shù)目。樽海鞘群算法中位置向量X將由維度為d的N個(gè)樽海鞘個(gè)體組成。因此，種群向量由N×d維矩陣構(gòu)成，如下公式所示：

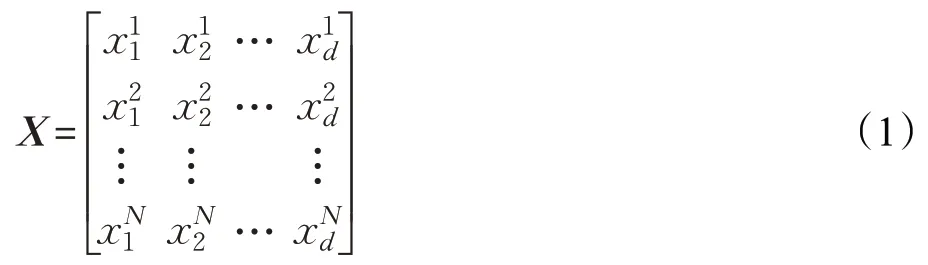
在樽海鞘群算法中，食物源的位置是所有樽海鞘個(gè)體的目標(biāo)位置。因此，領(lǐng)導(dǎo)者的位置更新公式如下所示：

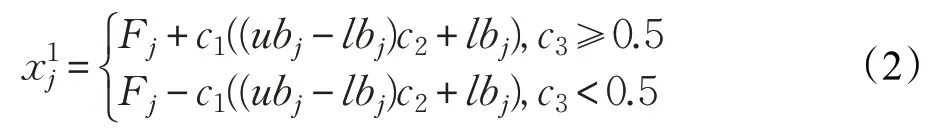
由式（2）可知，領(lǐng)導(dǎo)者位置更新主要受到食物源位置影響。系數(shù)c1是樽海鞘群算法中最重要的參數(shù)，可以使SSA 的探索能力和開發(fā)能力處于平衡狀態(tài)，其定義如下：

式中，t為當(dāng)前迭代次數(shù)，Tmax為最大迭代次數(shù)。

在求解測試函數(shù)優(yōu)化問題中，搜索范圍變化大。為了使樽海鞘群算法前期搜索具有更好的全局性和隨機(jī)性，本文選取多個(gè)領(lǐng)導(dǎo)者來進(jìn)行更新，但領(lǐng)導(dǎo)者太多，算法隨機(jī)性較強(qiáng)，這會(huì)導(dǎo)致算法穩(wěn)定性降低，因此為了權(quán)衡算法的隨機(jī)性和穩(wěn)定性，本文選取一半的樽海鞘個(gè)體作為領(lǐng)導(dǎo)者。

為了更新追隨者的位置，使用以下公式（牛頓運(yùn)動(dòng)定理）：

因此，由式（2）和式（5）可以模擬樽海鞘鏈的行為機(jī)制。

3 混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法

3.1 改進(jìn)Tent映射的種群初始化

樽海鞘群體的初始化對SSA 算法的收斂速度和尋優(yōu)精度至關(guān)重要。在樽海鞘群初始時(shí)，由于沒有任何先驗(yàn)知識可使用，基本上大部分群智能算法的初始位置都是隨機(jī)生成。文獻(xiàn)[17]提出初始種群均勻分布在搜索空間，對提高算法尋優(yōu)有很大幫助。

混沌序列具有隨機(jī)性、遍歷性和規(guī)律性等特點(diǎn)，通過其產(chǎn)生的樽海鞘群體有較好的多樣性。其基本思路是，通過映射關(guān)系在[0，1]區(qū)間產(chǎn)生混沌序列，然后再將其轉(zhuǎn)化到個(gè)體的搜索空間。產(chǎn)生混沌序列的模型有許多，文獻(xiàn)[18]提出，Tent 映射比 Logistic 映射能夠生成更好的均勻序列。但Tent 映射產(chǎn)生的混沌序列存在小周期和不確定周期點(diǎn)等缺點(diǎn)。為克服此類缺陷，在原有的Tent混沌映射中加入一個(gè)隨機(jī)變量r/N，改進(jìn)后的Tent映射的數(shù)學(xué)表達(dá)式為：

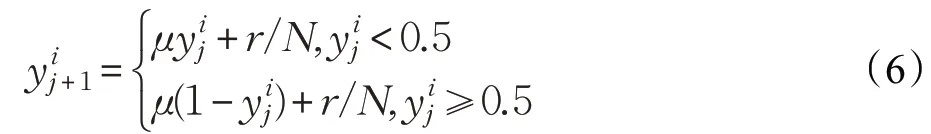
其中，r為[0，1]之間的隨機(jī)數(shù)；μ∈[0,2]是混沌參數(shù)，μ越大，混沌性越好，本文取μ=2；i=1,2,…,N表示種群規(guī)模；j=1,2,…,d表示混沌變量序號。

Tent 混沌映射對初始值的選取非常敏感，給式（6）選取d個(gè)具有微小差異的初始值，則可得到d個(gè)混沌序列。然后再將d個(gè)混沌序列進(jìn)行逆映射，得到相應(yīng)的個(gè)體搜索空間變量。

其中，[lbi,ubi]為的搜索范圍。

3.2 精英質(zhì)心拉伸機(jī)制

文獻(xiàn)[16]提出重心反向?qū)W習(xí)策略，利用種群的重心生成反向解，以更好利用群體信息。雖然這樣考慮到利用整個(gè)群體的信息，但包含的個(gè)體信息較多，算法運(yùn)行成本較大。本文提出精英質(zhì)心拉伸機(jī)制，選取群體中m個(gè)精英個(gè)體，求解其質(zhì)心，然后根據(jù)質(zhì)心對精英個(gè)體進(jìn)行拉伸機(jī)制。質(zhì)心和拉伸機(jī)制定義如下：

定義1（質(zhì)心）設(shè)(x1,x2,…,xn)為D維搜索空間中n個(gè)個(gè)體，則其整體的質(zhì)心定義為：

即得：

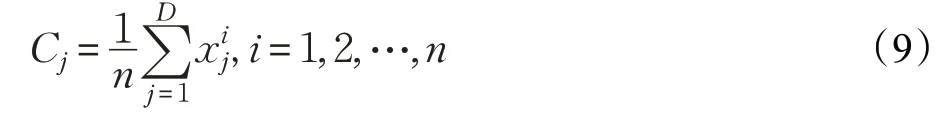
定義2（拉伸機(jī)制）若精英個(gè)體的質(zhì)心為C，則某個(gè)精英個(gè)體xi的拉伸點(diǎn)定義為：

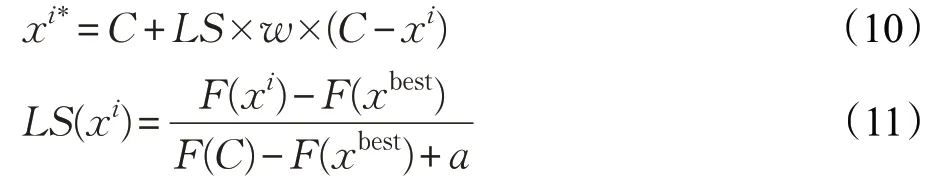
式中，w為[-1,1]之間的隨機(jī)數(shù)，a為一個(gè)極小的正數(shù)，F(xiàn)為適應(yīng)度函數(shù)，LS為拉伸因子，衡量精英個(gè)體與全局最優(yōu)個(gè)體的差異程度，引導(dǎo)精英個(gè)體向質(zhì)心個(gè)體學(xué)習(xí)。

由上述精英質(zhì)心拉伸機(jī)制可以發(fā)現(xiàn)，利用精英個(gè)體的質(zhì)心，作用于精英個(gè)體本身，以提升精英個(gè)體的性能。本文對當(dāng)前種群中適應(yīng)度最好的前m個(gè)精英個(gè)體運(yùn)用拉伸機(jī)制。精英質(zhì)心拉伸機(jī)制可從以下兩方面增強(qiáng)算法性能：首先，將拉伸后新群體與當(dāng)前群體融合，選出融合后一半的最優(yōu)個(gè)體進(jìn)入下一代種群中，以增強(qiáng)群體的多樣性，可減小算法陷入局部最優(yōu)的概率；其次，充分利用當(dāng)前群體中精英個(gè)體搜索空間的有效信息，以此加快算法的收斂速度。由此可見，精英質(zhì)心拉伸機(jī)制可較好平衡算法的探索和開發(fā)能力。

3.3 CESSA算法步驟

混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法步驟如下：

步驟1 初始化個(gè)體位置。使用改進(jìn)的Tent 映射生成混沌序列，根據(jù)搜索空間的上下限，再把混沌序列逆映射為一個(gè)N×d維的矩陣。

步驟2 計(jì)算初始適應(yīng)度值。根據(jù)測試函數(shù)計(jì)算N個(gè)樽海鞘的適應(yīng)度值。

步驟3 選定食物源。把步驟2 中計(jì)算后的適應(yīng)度值進(jìn)行升序（或降序）排列，適應(yīng)度值最好的樽海鞘位置選定為食物源位置。

步驟4 領(lǐng)導(dǎo)者和追隨者位置更新。確定食物源位置之后，選取種群中一半的樽海鞘個(gè)體根據(jù)式（2）更新領(lǐng)導(dǎo)者位置，其余的樽海鞘根據(jù)式（5）更新追隨者位置。

步驟5 精英質(zhì)心拉伸機(jī)制。利用3.2節(jié)定義2所描述的精英質(zhì)心拉伸的方法對當(dāng)前種群中m個(gè)精英個(gè)體求解拉伸解，并比較更新每個(gè)樽海鞘個(gè)體的位置。

步驟6 計(jì)算適應(yīng)值。計(jì)算更新后種群的適應(yīng)度值，并更新食物源位置。

步驟7 重復(fù)步驟4～步驟6的更迭過程，如果達(dá)到設(shè)置的精度要求或規(guī)定的最大迭代次數(shù)，則終止算法，輸出全局最優(yōu)解。

4 仿真實(shí)驗(yàn)與結(jié)果分析

為驗(yàn)證本文提出的CESSA算法在求解優(yōu)化問題上的有效性和魯棒性，將CESSA 算法與SSA、PSO 以及GA 在12 個(gè)典型的標(biāo)準(zhǔn)測試函數(shù)最優(yōu)值求解上獨(dú)立進(jìn)行50 次對比實(shí)驗(yàn)1。另外還在CEC2014 基準(zhǔn)函數(shù)中選取部分函數(shù)進(jìn)行對比實(shí)驗(yàn)2。

實(shí)驗(yàn)1 采用如表1 所示的12 個(gè)復(fù)雜函數(shù)作為適應(yīng)度函數(shù)。選取的測試函數(shù)中包含單峰、多峰等不同特征的測試函數(shù)。單峰函數(shù)為在定義上下限內(nèi)只有一個(gè)嚴(yán)格上的極大值（或極小值），通常用來檢測算法收斂速度。多峰函數(shù)為含有多個(gè)局部最優(yōu)解或全局最優(yōu)解的函數(shù)，經(jīng)常用于檢測算法探索能力和開發(fā)能力。另外，測試函數(shù)的求解維度也是一個(gè)重要因素，算法對低維度求解質(zhì)量好時(shí)對高維度不一定也好。表1 中測試函數(shù)維度從2維到200維，這可以更加全面地驗(yàn)證算法性能。

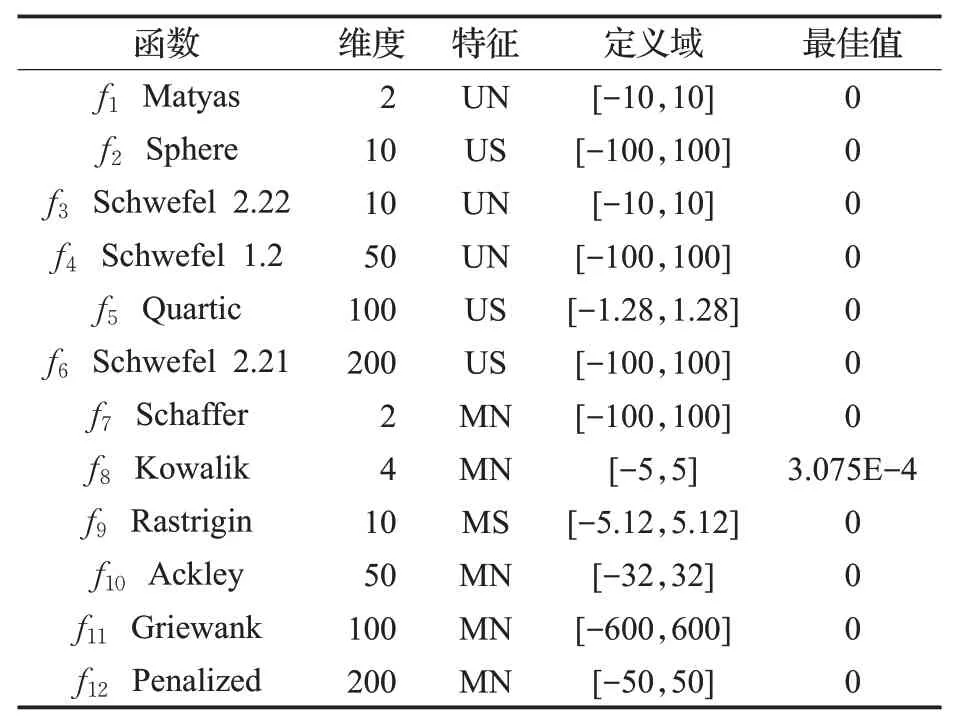
表1 基準(zhǔn)函數(shù)

實(shí)驗(yàn)環(huán)境為：Windows7系統(tǒng)，8GB內(nèi)存，CPU 2.5GHz，算法基于Matlab14b用M語言編寫。

實(shí)驗(yàn)設(shè)置最大迭代次數(shù)為1 000，初始樽海鞘群、粒子群和染色個(gè)體的規(guī)模都為30。對于CESSA、SSA、PSO和GA算法的其他相關(guān)參數(shù)設(shè)置如表2所示。

表2 算法參數(shù)設(shè)置

表3 記錄了50 次獨(dú)立實(shí)驗(yàn)后從每種算法獲得結(jié)果的最佳值（Best）、平均值（Mean）和標(biāo)準(zhǔn)偏差（Std）以及求解成功率（Successful Rate，SR）和平均耗時(shí)（Time）等多個(gè)實(shí)驗(yàn)對比數(shù)據(jù)。其中求解成功率為計(jì)算成功次數(shù)除以本次實(shí)驗(yàn)的求解次數(shù)。判斷一次求解是否成功按照下式：

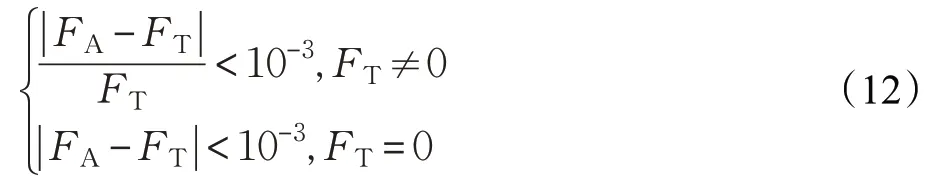
式中，F(xiàn)A為每次實(shí)際求解最佳值，F(xiàn)T為測試函數(shù)理論最佳值。

首先，表3 中的最優(yōu)值、平均值都可以反映算法的收斂精度和尋優(yōu)能力。對于6 個(gè)單峰函數(shù)(f1～f6) ，CESSA算法在求解精度上最高達(dá)到1E-33。同時(shí)，隨著搜索空間維度的增加，尋優(yōu)收斂精度4 種算法都在下降。另外標(biāo)準(zhǔn)SSA 算法在求解f4的時(shí)候，SSA 算法的求解能力就很差，與理論最優(yōu)值存在1E+03 級的誤差。而 CESSA 相對于 SSA、PSO 和 GA 尋優(yōu)精度都要好，并且其求解精度變化不大。伴隨求解維度的增加，對于算法求解難度也呈指數(shù)級別遞增，算法的收斂精度有所降低屬于正常現(xiàn)象。對于6個(gè)多峰函數(shù)(f7～f12)，算法求解精度相對于單峰函數(shù)要低一些。同樣，隨著維度增加，算法求解精度也有所降低。當(dāng)維度增加到200 維時(shí)，CESSA算法求解f12的精度降到1E-01，但CESSA算法較其他三種算法仍然具有很好的優(yōu)勢。因此，CESSA算法在求解單峰、多峰以及高維的基準(zhǔn)函數(shù)時(shí)都有更好的尋優(yōu)效果和魯棒性。

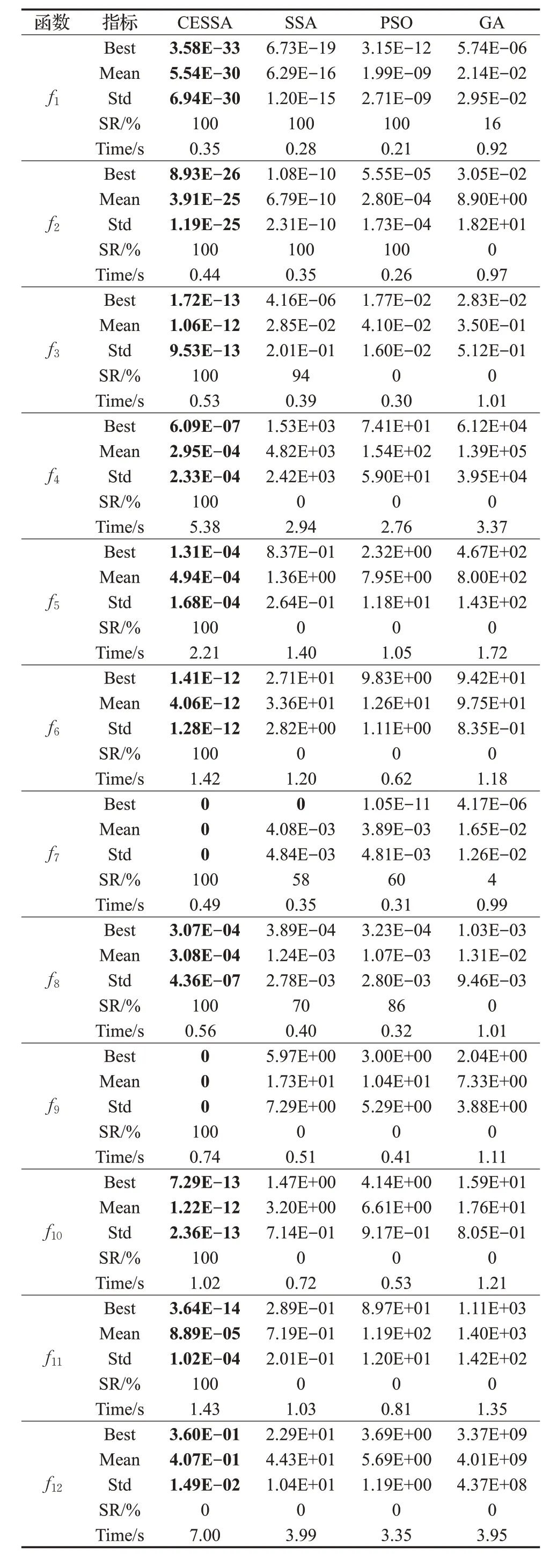
表3 各算法基準(zhǔn)函數(shù)的結(jié)果對比

其次，表3～表5中標(biāo)準(zhǔn)差和成功率可以反映算法的穩(wěn)定性和跳出局部最優(yōu)的能力。在f12函數(shù)的求解上，CESSA 算法的尋優(yōu)結(jié)果和理論結(jié)果還存在精度不足，但CESSA算法獨(dú)立50次計(jì)算的標(biāo)準(zhǔn)差基本比其他三種算法都要小。這說明CESSA算法對于低維和高維基準(zhǔn)函數(shù)的尋優(yōu)求解有著很好的穩(wěn)定性，且在多峰函數(shù)上尋優(yōu)能力比較強(qiáng)，跳出局部最優(yōu)的能力相對于其他算法更好些。6個(gè)基準(zhǔn)函數(shù)中有單峰、多峰、低維和高維，除了求解200 維成功率較差，CESSA 在成功率上基本為100%，而標(biāo)準(zhǔn)SSA在f1和f2這兩個(gè)基準(zhǔn)函數(shù)的成功率為100%以外，其余基準(zhǔn)函數(shù)成功率全部為0。隨著搜索維度的增加，標(biāo)準(zhǔn)SSA在尋優(yōu)求解能力上表現(xiàn)著很大不足。特別是在求解多維函數(shù)時(shí)，標(biāo)準(zhǔn)差和成功率都較差，說明標(biāo)準(zhǔn)SSA 跳出局部最優(yōu)的能力是較弱。而在CESSA 中引入精英質(zhì)心拉伸機(jī)制后，這對算法后期跳出局部搜索具有很大作用。

再次，從平均耗時(shí)來看。由表3可知，改進(jìn)的CESSA算法相對于標(biāo)準(zhǔn)SSA的平均耗時(shí)都要大，PSO算法和標(biāo)準(zhǔn)SSA算法互有優(yōu)劣，但總體運(yùn)行時(shí)間均要優(yōu)于CESSA算法和GA 算法。CESSA 算法在SSA 種群更新后引入精英質(zhì)心拉伸算子，使得算法能夠搜索到更多的解，這也就增加了算法運(yùn)行時(shí)間。總體來看，CESSA 平均耗時(shí)比另外兩種算法增加得并不是很大，在允許范圍內(nèi)。

Derrac 等在文獻(xiàn)[19]中提出，對于改進(jìn)進(jìn)化算法性能的評估，應(yīng)該進(jìn)行統(tǒng)計(jì)檢驗(yàn)。換而言之，僅基于平均值和標(biāo)準(zhǔn)偏差值來比較算法優(yōu)劣還不夠，需要進(jìn)行統(tǒng)計(jì)檢驗(yàn)以證明所提出的改進(jìn)算法比其他現(xiàn)有算法具有顯著的改進(jìn)優(yōu)勢。為了判斷CESSA的每次結(jié)果是否統(tǒng)計(jì)上顯著地與其他算法的最佳結(jié)果不同，Wilcoxon 秩和檢驗(yàn)在5%的顯著性水平下進(jìn)行。表4給出所有基準(zhǔn)函數(shù)的最優(yōu)值和其他算法的Wilcoxon 秩和檢驗(yàn)中計(jì)算的p-value。例如，如果最佳算法是CESSA，則只在CESSA/SSA，CESSA/PSO、CESSA/GA 等之間進(jìn)行成對比較。由于最佳算法無法與自身進(jìn)行比較，針對每個(gè)函數(shù)中的最佳算法標(biāo)記為N/A，表示“不適用”。這意味著相應(yīng)的算法可以在秩和檢驗(yàn)中沒有統(tǒng)計(jì)數(shù)據(jù)與自身進(jìn)行比較。根據(jù)Derrac等人的論文，那些p-value<0.05的可以被認(rèn)為是拒絕零假設(shè)的有力驗(yàn)證。

表4 Wilcoxon秩和檢驗(yàn)的p-value

根據(jù)表4 中的結(jié)果，CESSA 算法的p-value全部小于0.05，這表明該算法的優(yōu)越性在統(tǒng)計(jì)上是顯著的，即認(rèn)為CESSA算法比SSA、PSO、GA具有更高的收斂精度。

所有算法的定量分析是基于12個(gè)基準(zhǔn)函數(shù)的平均絕對誤差（Mean Absolute Error，MAE）。文獻(xiàn)[20]提出對優(yōu)化算法進(jìn)行排序，MAE 是一種有效且可行的性能指標(biāo)。表5 給出了這些基準(zhǔn)函數(shù)的MAE 排序，其計(jì)算公式如下：

式中，mi為算法產(chǎn)生的最優(yōu)結(jié)果的平均值，oi為相應(yīng)基準(zhǔn)函數(shù)的理論最優(yōu)值，Nf為基準(zhǔn)函數(shù)個(gè)數(shù)。計(jì)算出的MAE在表5中給出。

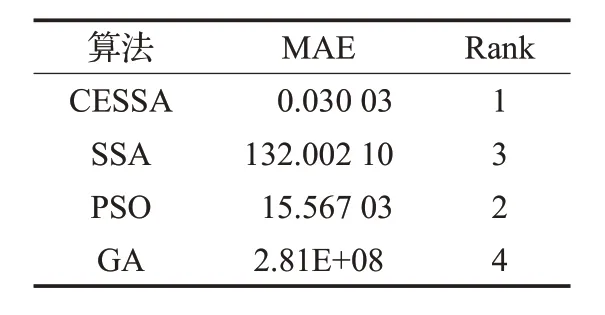
表5 MAE算法排名

由表5 可知，CESSA 排名為1，與另外三種算法相比，CESSA 提供了最小的MAE，進(jìn)一步說明了CESSA的有效性。

圖1給出4個(gè)基準(zhǔn)函數(shù)的平均收斂曲線。由于不同算法收斂精度存在較大差異，為便于觀察收斂情況，本文對尋優(yōu)適應(yīng)度值（縱坐標(biāo)）取10 為底的對數(shù)。由圖1（a）、（b）可看出，CESSA 算法的收斂曲線下降較快，并隨著更迭次數(shù)的增加持續(xù)尋優(yōu)，只在后期出現(xiàn)停滯。從圖1（a）、（b）可知，GA、PSO和SSA在迭代后期出現(xiàn)不同程度的停滯，且尋優(yōu)精度較低。圖1（c）、（d）是多峰函數(shù)的平均收斂曲線。從CESSA 算法的收斂性上可以看出，在f11上迭代前期收斂速度比較平緩，后期收斂速度較快。在f8函數(shù)上，CESSA算法在前期收斂速度較快，但算法前期收斂速度相對于PSO較慢。CESSA后期出現(xiàn)一定程度停滯，但收斂精度比另外三種算法要好。從圖中還可以看出，SSA、PSO和GA在后期基本都陷入局部最優(yōu)，但CESSA 算法最終的尋優(yōu)精度較其他算法仍然表現(xiàn)較好。無論單峰、多峰，還是低維和高維，對于每個(gè)基準(zhǔn)函數(shù)CESSA比其他算法的收斂速度和尋優(yōu)精度要好。

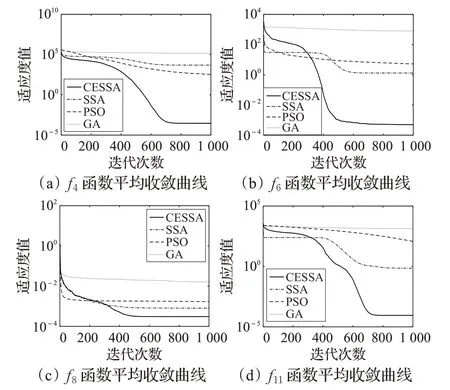
圖1 部分基準(zhǔn)函數(shù)平均收斂曲線

實(shí)驗(yàn)2 為更好評估CESSA 算法的有效性和穩(wěn)定性。本文還在CEC2014 基準(zhǔn)函數(shù)中選取部分單峰、多峰、混合（Hybrid）和復(fù)合（Composition）類型的函數(shù)進(jìn)行優(yōu)化求解，如表6所示。在該實(shí)驗(yàn)中，種群規(guī)模為30，最大迭代次數(shù)為500，維度為30。

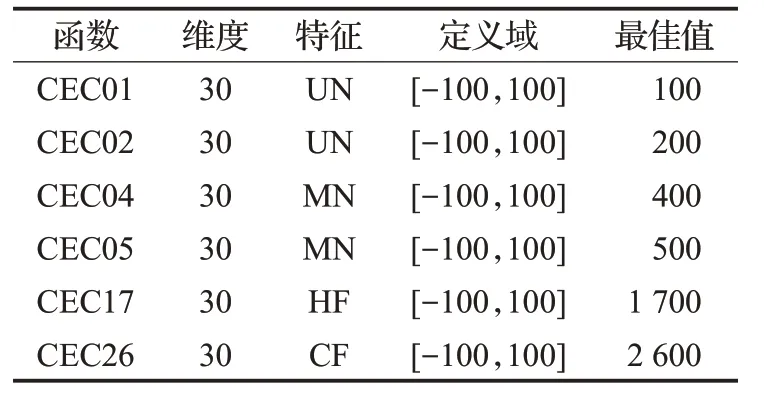
表6 CEC2014基準(zhǔn)函數(shù)

表7 記錄了CEC2014 中部分函數(shù)獨(dú)立運(yùn)行30 次后每種算法的平均值和標(biāo)準(zhǔn)差的結(jié)果對比。CEC2014 函數(shù)具有復(fù)雜的特征，因此所有算法都較難找到函數(shù)最優(yōu)值。表7中結(jié)果顯示，CESSA算法在6個(gè)CEC2014基準(zhǔn)函數(shù)上都求得比其他三種算法更優(yōu)的結(jié)果，進(jìn)一步驗(yàn)證了CESSA算法具有較好的有效性和魯棒性。

為比較本文改進(jìn)算法與其他改進(jìn)算法的優(yōu)劣性，將CESSA 算法與參考文獻(xiàn)[8]和文獻(xiàn)[10]中改進(jìn)算法進(jìn)行比較，其中直接引用了文獻(xiàn)[10]中CSSA1的數(shù)據(jù)，如表8所示（“—”表示參考文獻(xiàn)中未給出）。表1 基準(zhǔn)測試函數(shù)中可變維度函數(shù)的dim 都設(shè)置為10，種群數(shù)目為50，最大迭代次數(shù)為500。

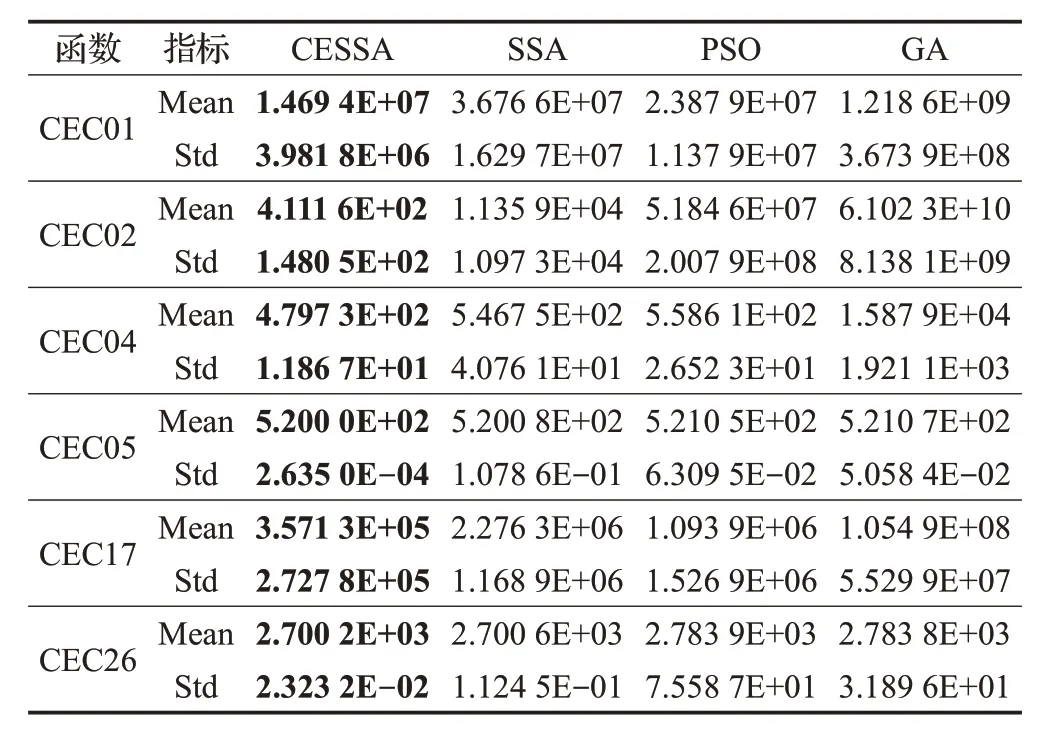
表7 CEC2014優(yōu)化結(jié)果對比

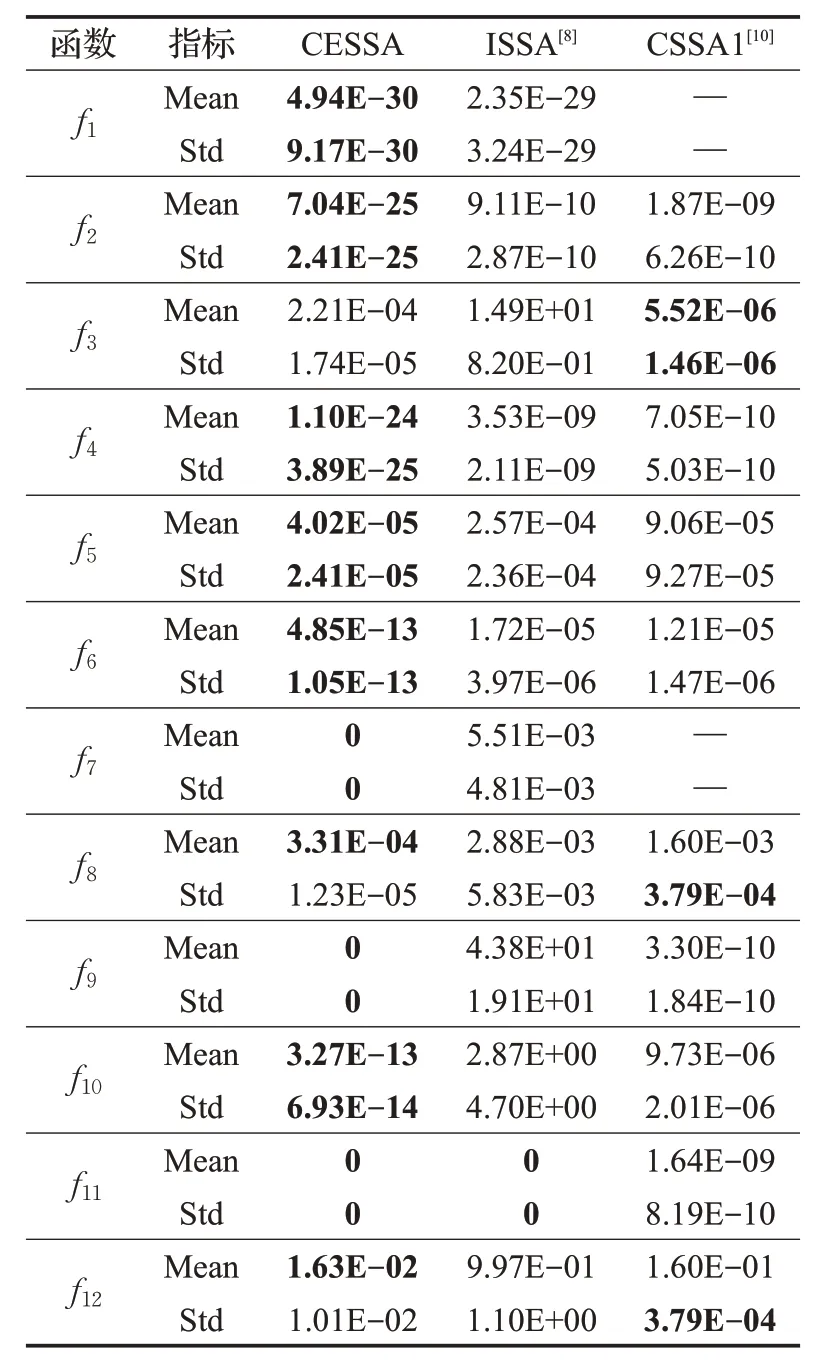
表8 與參考文獻(xiàn)中算法性能的對比

由表 8 可知，除了在求解f3、f8、f12時(shí)，文獻(xiàn)[10]算法的標(biāo)準(zhǔn)差好于CESSA算法，本文提出的CESSA算法在求解其他函數(shù)時(shí)的平均值和標(biāo)準(zhǔn)差都要好于文獻(xiàn)[8]和文獻(xiàn)[10]改進(jìn)算法，進(jìn)一步驗(yàn)證了CESSA 算法的有效性。

綜上可知，混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法對本文所選取的基準(zhǔn)函數(shù)都有很好的尋優(yōu)結(jié)果，特別是對于高維、多峰的函數(shù)，具有較好的穩(wěn)定性和尋優(yōu)能力。

5 結(jié)束語

本文在標(biāo)準(zhǔn)樽海鞘群算法的基礎(chǔ)上，引入改進(jìn)的混沌映射和精英質(zhì)心拉伸機(jī)制，提出一種改進(jìn)的混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法，并將樽海鞘群算法應(yīng)用于經(jīng)典測試函數(shù)和CEC2014函數(shù)的尋優(yōu)問題中。本文不僅使用最優(yōu)值、標(biāo)準(zhǔn)差等指標(biāo)對算法進(jìn)行檢驗(yàn)，還提出使用Wilcoxon 秩和檢驗(yàn)對算法顯著性水平進(jìn)行驗(yàn)證。研究表明：基于混沌精英質(zhì)心拉伸機(jī)制的樽海鞘群算法可以獲得更好的全局搜索和局部搜索能力，且可以收斂到質(zhì)量更好的最優(yōu)解，算法的有效性和魯棒性也得到驗(yàn)證。