兩種多粒度形式概念分析模型的比較研究

折延宏，胡夢婷，賀曉麗，曾望林

1.西安石油大學 理學院，西安 710065

2.西安石油大學 計算機學院，西安 710065

1 引言

形式概念分析[1]是一種進行數據分析的有效數學工具，其核心概念為形式背景、形式概念與概念格。通過概念格所展現出的概念之間的特化與泛化關系，揭示了數據表的內在結構，刻畫了對象與屬性之間的依賴關系。

近年來，一個有趣的研究方向是將多粒度計算的思想融入到形式概念分析之中，由此產生了不同的多粒度形式概念分析模型[2-16]。形式概念分析的粒計算方法包括形式背景的對象粒化[2]、屬性粒化[3-8]、關系粒化[9-11]等，這些方法除了可以緩解龐大的概念個數之外，還可以獲取數據的多層次概念知識表示與處理方法[12]。

本文主要關注的是形式概念分析的屬性粒化方法。屬性粒化意味著屬性的合并（或提升）、分解（或細化），通過屬性粒化可實現知識的粗細轉換，使人們在不同粒度的形式背景上進行概念分析。Belohlavek 等人在文獻[3]中提出了基于屬性粒化的形式概念分析方法，在該方法中，一個屬性在不同粒度下可劃分為不同的子屬性，利用粒度樹與剪枝（cut）等主要工具可導出不同粒度層次的形式背景，基于此，實現了在不同粒度層次下對數據的分析[3-5，15]。與此不同的是，基于屬性聚類的多粒度形式概念分析模型是通過屬性集上的先驗知識或先驗關系R實現的。文獻[6]通過屬性集上的一等價關系實現了屬性的聚類，進而研究了聚類前后概念之間的內在聯系與生成方式。可以說，文獻[3]與文獻[6]提出的方法迥然不同，前者通過粒度樹、剪枝等方法實現，后者通過對屬性聚類實現。本文對這兩種不同的方法進行分析對比。

2 基于屬性聚類與屬性粒化的形式概念分析方法

2.1 形式概念分析的基本知識

三元組(G,M,I)為一形式背景。其中G為一非空有限對象集，M為一非空有限屬性集，為與M之間的一二元關系，按如下方式定義兩映射↑:2G→2M與↓:2M→2G:

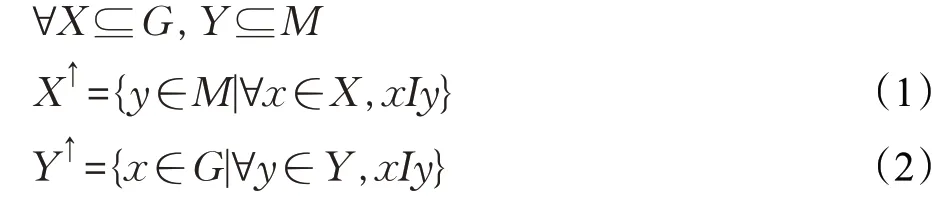
若X↑=Y,Y↓=X,則稱(X,Y)為一形式概念，也稱為Wille 概念。全體形式概念之集L(G,M,I)在如下偏序關系下構成一格，簡稱為概念格：

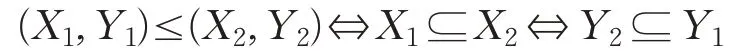
文獻[17-18]通過將粗糙近似算子引入到形式概念分析之中，引入了面向對象的形式概念分析模型，其概念生成算子是按照如下方式定義的：

若X□=Y,Y?=X,則稱(X,Y)為一形式概念，也稱為面向對象概念。全體面向對象概念之集Lο(G,M,I)在如下偏序關系下構成一格，簡稱為概念格：

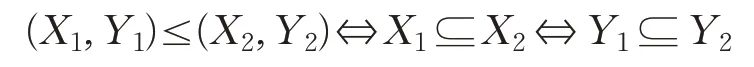
以下命題給出了如上兩種不同概念的性質，這種性質在本文的后續證明中起著重要的作用。

命題1[17-18]設(G,M,I)為一形式背景，?X?G,Y?M：

（1）(X↑↓,X↑)∈L(G,M,L),(Y↓,Y↓↑)∈L(G,M,L)

（2）(X□?,X□)∈Lο(G,M,L),(Y?,Y?□)∈Lο(G,M,L)

（3）X?X↑↓,Y∈Y↓↑

定義1 若在M1與M2之間的一一映射f:M1→M2,使得 ?g∈G,m1∈M1,gI1m1當且僅當gI2f(m1),則稱兩形式背景(G,M1,I1)與(G,M2,I2)是同構的。

在一一對應關系中不區分屬性的情況下，可將兩同構的形式背景視為相同的。

2.2 基于屬性聚類的形式概念分析方法

如文獻[6，12]中所述，通常情況下，根據某個特定需求，或基于先驗知識，可將形式背景中的屬性集聚在一起，形成更高一級的屬性。數學上，這一想法可通過屬性集上的等價關系來實現。基于等價關系，可將部分屬性聚合在一起形成一個新的屬性，由此可導出一個新的形式背景。與原形式背景相比，對象集是相同的，但屬性集發生了變化，由此可在不同層次、不同粒度下進行概念分析。

具體地，設(G,M,I)為一形式背景，R為M上的等價關系，[m]R為包含m的屬性等價類。基于(G,M,I)與R，可構造如下形式背景(G,MR,IR)，其中：

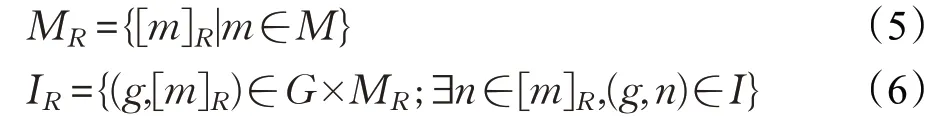
注意到：[m]R雖然是由形式背景(G,M,I)中的若干屬性組成的，但在形式背景(G,MR,IR)中，它只是作為一個屬性。此外，IR的定義與I有著密切的聯系，在新的形式背景(G,MR,IR)中，對象g與屬性[m]R具有關系IR當且僅當g與該等價類中某一個屬性在原形式背景中具有關系I。

在新的形式背景(G,MR,IR)中，可定義如下形式的概念生成算子：

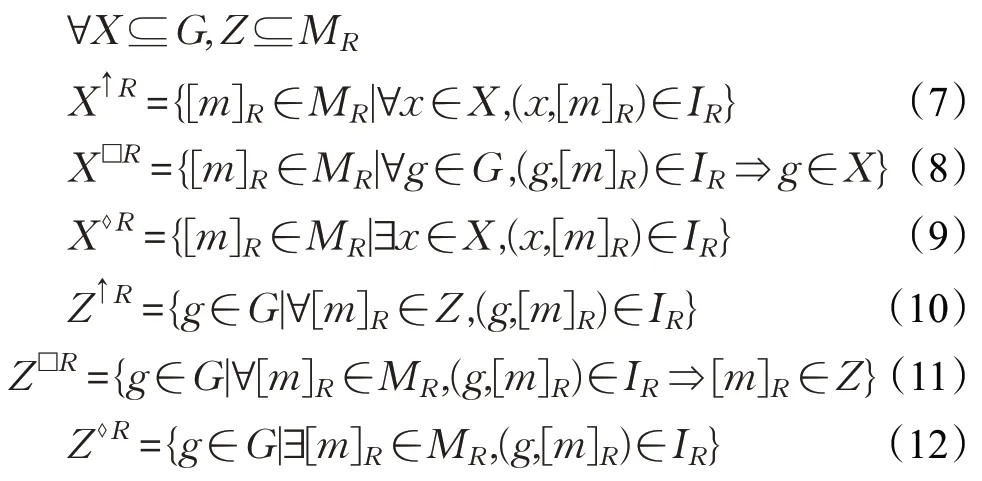
2.3 基于屬性粒化的形式概念分析方法

文獻[3]提出了一種基于屬性粒化的形式概念分析方法。在該方法中，原形式背景(G,M,I)中的每一個屬性在不同的粒度下可分解為不同的子屬性，這些不同粒度的屬性形成了一粒度樹，文獻[3]借助粒度樹以及粒度樹中的剪枝方法，從原背景出發導出了不同粒度的形式背景，為在不同粒度下進行概念分析提供了一個可能的框架。

定義2[3]設K=(G,M,I) 為一形式背景，m∈M。屬性m的粒度樹Tm是滿足如下條件的一個含有根節點的樹：

（l）樹中的每一個節點都用一個屬性名稱來標記，根節點記作m；

（2）對于每一個節點z，賦予一對象集合{z}↓?G,該對象集{z}↓由具有屬性z的對象所構成；

（3）若z1,z2,…,zn是節點z的子節點，則 {{z1}↓,{z2}↓,…,{zn}↓}是 {z}↓的一個劃分。

為方便起見，往往用z↓，而不用{z}↓，其含義是不變的。

定義3[3]粒度樹Tm中的一剪枝（原文稱之為cut）C是滿足如下條件的一節點集：對于每一個葉節點u而言，在從u到根節點m的路徑上，存在唯一的節點v屬于C。

例1 表1給出了一基于屬性粒化的形式背景，在該表中，屬性G具有兩層粒度，圖1給出了粒度樹TG中的所有剪枝，即{G}與{IG,dG}。注意到C={G,dG}并不是粒度樹TG的一剪枝，其原因在于從葉節點dG到根節點G的路徑上，存在兩個節點屬于C。同理，{G,IG}也不是一剪枝。

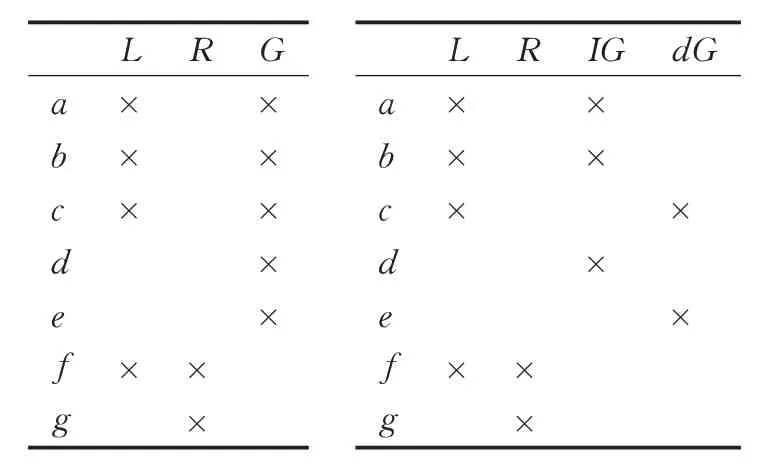
表1 基于屬性粒化的形式背景

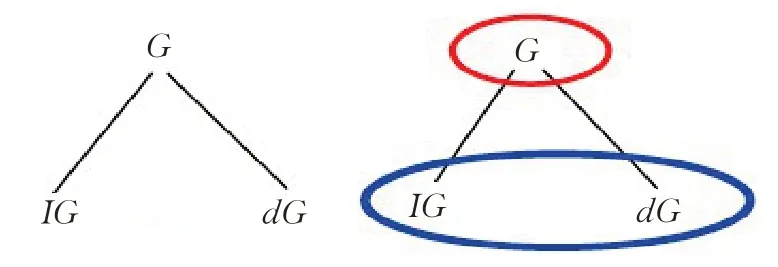
圖1 表1中的粒度樹以及剪枝?z ∈MC,(g,m)∈IC ?g ∈m↓

由定義2、定義3 以及例1 可見，每一個屬性都有唯一的粒度樹，但每一個粒度樹上有不同的剪枝。在同一屬性粒度Tm的剪枝集上定義如下偏序關系：C1={y1,y2,…,yr},C2={z1,z2,…,zs}∈Tm,C1≤C2當且僅當是的細化，即=是通過對中每個集合進一步劃分后得到的。

設(G,M,I)為一形式背景，對于每一個屬性m∈M而言，Tm為其粒度樹，Cm是Tm上的一剪枝，不同屬性粒度樹上的剪枝可導出如下一形式背景(G,MC,IC)，其中。

在每個屬性的粒度樹上任意選取一剪枝，所有這些剪枝之集C代表了特定的屬性粒化層次（Granularity Level）。對于任意兩屬性粒化層次C1與C2，用C1≤C2表示 ?m∈M，C1m≤C2m,這里C1m與C2m分別表示屬性m在兩粒化層次中的剪枝。換言之，C1是C2的細化。由此，可在不同的粒化層次上進行概念分析。

在新的形式背景(G,MC,IC)中，可定義如下形式的概念生成算子：

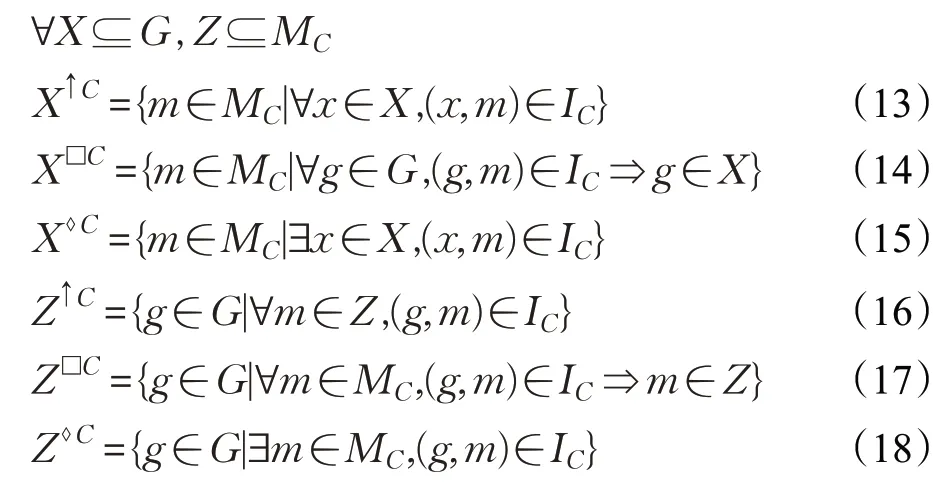
為以下討論方便，引入如下記號：設C1、C2為滿足C1≤C2的兩剪枝，對于用表示m1在中的父節點，用表示中的子節點集。

3 不同多粒度方法的比較研究

3.1 Wille概念模型框架內兩方法的比較研究

由上文的介紹可以看得出，基于屬性粒化與基于屬性聚類的多粒度形式概念分析方法有著較為顯著的差異，本節進一步分析兩者的區別與內在聯系。

定理1 設(G,M,I)為一形式背景，R為M上的一等價關系，則對于任意(A,B)∈L(G,MR,IR),存在(Ak,Bk)∈L(G,M,I)(k∈K)使得A=∪i∈K Ak。

證明對于(A,B)∈L(G,MR,IR)，以下分兩種情形進行證明。

情形1B≠?：此時不妨設B={[y1]R,[y2]R,…,[yn]R}。任意(m1,m2,…,mn)∈[y1]R×[y2]R×…×[yn]R,令(Ak,Bk)=({m1,m2,…,mn}↓，{m1,m2,…,mn}↓↑)。以下證明 (Ak,Bk)為滿足條件的形式概念。

事實上，由命題1 知(Ak,Bk)∈L(G,M,I)。以下證明A=∪Ak。首先證明∪Ak?A。對于任意對象g∈G,若g∈∪Ak,即存在 (m1,m2,…,mn)∈[y1]R×[y2]R×…×[yn]R使得g∈{m1,m2,…,mn}↓,由式（2）知g同時具有屬性m1,m2,…,mn,結合式（6）知g同時具有形式背景中的屬性 [y1]R,[y2]R,…,[yn]R,因此，g∈B↓R={[y1]R,[y2]R,…,[yn]R}↓R,即g∈A。反過來，任取g∈A,由A=B↓R={[y1]R,[y2]R,…,[yn]R}↓R知g同時具有 (G,MR,LR)中屬性[y1]R,[y2]R,…,[yn]R，由式（6）知必存在 (m1,m2,…,mn)∈[y1]R×[y2]R× … ×[yn]R使得gImi,i=1,2,…,n,因此，g ∈{m1,m2,…,mn}↓,即g屬于某一Ak。綜上A=∪i∈K Ak。

情形2B=?：此時易知A=G,對于G中每個對象g而言，({g}↑↓,{g}↑)屬于L(G,M,I)，且g∈{g}↑↓（命題1），因此G=∪g∈G{g}↑↓,得證。

以下將說明文獻[3]的概念分解定理可看作定理1的特殊情形。首先注意到如下事實成立：在文獻[3]中，C1≤C2意味著中每一屬性都在中存在劃分子屬性，即使得從屬性聚類的角度看，可看作是原背景，通過將中每個屬性的劃分子屬性聚為一類，便可得到形式背景

兩種不同背景下的概念分析算子有著密切的聯系，這由如下命題可以看得出。

命題2 設(G,M,I)為一形式背景，C1、C2為兩剪枝且C1≤C2,在上定義二元關系則：

（1）R為上的一等價關系；

（3）在同構意義下，?X?G,X↑C2=X↑R。

證明（1）容易驗證R滿足自反性、對稱性以及傳遞性，因此R為一等價關系。

（2）定 義 映 射容易驗證f為一映射，在不區分m與f(m)的前提下，以下證明事實上，對于G中任意對象g以及中屬性m2，若，由于中屬性是中相應屬性的劃分，因此存在中屬性z1使得，根據式（6）得故反過來，若由式（6）知存在[z]R中某一屬性z1使得，對于z1，必然存在中一父節點z2使得，由于與存在一一對應關系，在將[z]R與z2不加以區分的情況下，便有得證。

（3）由（2）可立即推得。

由命題2可得如下推論。

推論1 若C1≤C2,則對于任一形式概念∈存在形式概念集k∈K使得 ∪k∈K Ak=A。

證明若C1≤C2,由命題2 知形式背景可看作是對形式背景進行屬性聚類后得到的形式背景，則由定理1知結論成立。

注意到推論1 正是文獻[3]所述的分解定理。綜合以上結論，文獻[3]給出的基于屬性粒化的形式概念分析模型是本文提出的基于屬性聚類概念分析模型的特殊情形。

3.2 面向對象概念分析模型中兩種方法的比較

文獻[15]在多粒度形式背景中研究了面向對象的形式概念，將已有的面向對象概念由單粒度拓展至多粒度情形，研究了在不同粒度下，面向對象概念之間的內在聯系，證明了在不同粗細粒度下外延集相等的充分必要條件。

設(G,M,I)為一形式背景，對于任意屬性m∈M,有一粒度樹Tm,CM為Tm上一剪枝，不同粒度樹的剪枝（每個粒度樹上任意挑選一個剪枝）集可按之前的方式生成一形式背景(G,MC,IC),利用面向對象的概念生成算子（3）以及（4）可在不同的粒度下生成不同的面向對象概念格。本文用Lο(G,MC,IC)以及EXT(Lο(G,MC,IC))分別表示由形式背景(G,MC,IC)所生成的面向對象概念格以及外延集。

文獻中主要結論如下：

命題3[15]若C1≤C2,則

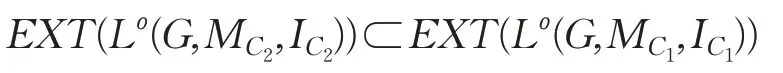
命題4[15]若C1≤C2,則

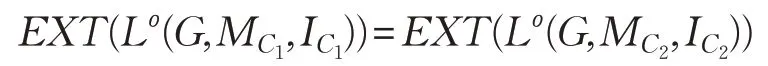
事實上，利用屬性聚類方法，可將文獻[15]中的面向對象的多粒度形式概念分析模型推廣至更為一般的情形。

定義4 設(G,M,I)為一形式背景，R為M上的一等價關系，(G,MR,IR)為其粒化后形式背景，X?G,Z?MR,若X□R=Z且Z?R=X,則稱 (X,Z)為 (G,MR,IR)中一面向對象的概念。

命題5 設(G,M,I)為一形式背景，R為M上的一等價關系，則EXT(Lο(G,MR,IR))?EXT(Lο(G,M,I))。

證明任取X∈EXT(Lο(G,MR,IR)),根據定義，存在Y ?MR使 (X,Y)∈Lο(G,MR,IR),即X□R=Y且Y?R=X。要證明X∈EXT(Lο(G,M,I)),等價于證明 (X,X□)∈L(G,M,I),或等價地，X□?=X。任取g∈X?R,由式（4）知，存在屬性m∈X□使得gIm，結合式（3）便知g∈X。反過來，任取g∈X，由Y?R=X知g∈Y?R,則存在[m]∈Y使gIR[m] ，結合IR的定義（即式（6））知存在m1∈[m]R使gIm1。以下說明m1∈X□,事實上，對于任意滿足gIm1的對象g而言，由gIR[m1]=gIR[m] 以及[m]∈Y，X□R=Y知g∈X,從而根據式（3）可得m1∈X□。再結合gIm1以及式（4）便知g∈X□?。

命題6 設(G,M,I)為一形式背景，R為M上的一等價關系，則對于任意X?G,X□R?X□,{[m]R|m∈X?}?X?R。

證明任取y∈X□R，則存在X□R中一等價類[m]R使得y∈[m]R。對于滿足gIy的任意對象g而言，gIR[m]R成立，結合[m]R∈X□R便知g∈X，因此 ∪X□R?X□。

任取 [y]R∈{[m]R|m∈X?} ，由g∈X?以及（4）知存在X中一對象g使得gIy，從而gIR[y]R，結合g∈X便知[y]R∈X?R，從而 {[m]R|m∈X?}?X?R。

命題7 設(G,M,I)為一形式背景，R為M上的一等價關系，則EXT(Lο(G,M,I))=EXT(Lο(G,MR,IR)),當且僅當對于任一等價類[m]R∈MR，存在Z?MR，使得對于任意。

證明充分性：對于形式背景(G,M,I)而言，由命題1知，對于任一外延X∈EXT(L(G,M,I))而言，存在Y?M使得X=∪mi∈Y y↓，又由題設條件知對于每一個屬性mi,存在Z?MR,使得對于任意，這樣，由命題1知X也屬于EXT(L(G,MR,IR))。結合命題5便知EXT(Lο(G,M,I))=EXT(Lο(G,MR,IR))。

必要性：若EXT(Lο(G,M,I))=EXT(Lο(G,MR,IR))，則對于EXT(Lο(G,M,I))中任一外延X,X也一定屬于EXT(Lο(G,MR,IR))，由命題1便知該結論成立。

事實上，類似于命題2，可以證明基于屬性粒化的面向對象概念分析模型可看作為基于屬性聚類的面向對象概念分析的特殊情形。

命題8 設(G,M,I)為一形式背景，C1、C2為兩剪枝且C1≤C2,在上定義二元關系，則：

（1）R為上的一等價關系；

證明可類似于命題2得證。

命題8告訴人們，對于屬性粒化中的兩剪枝C1、C2而言，若C1≤C2，則C2可看作是經過對C1中的屬性聚類得到的，兩種方法得到的面向對象概念近似算子是相等的。由命題8知，命題3可看作為命題5的特殊情形，命題7所得結論要比命題4更具一般性。

4 結束語

本文對多粒度形式概念分析中的兩種不同方法進行了分析對比，指出基于屬性粒化的方法可看作是已有的基于屬性聚類方法的特殊情形。下一步，可基于屬性聚類的方法設計有效的概念生成算法，也可以研究基于屬性聚類的多尺度信息表的規則提取方法。