大型游樂設施焊縫強度校核計算分析

趙九峰

大型游樂設施焊縫強度校核計算分析

趙九峰

（河南省特種設備安全檢測研究院，河南 鄭州 450000）

焊接是大型游樂設施的主要連接方式，焊縫設計計算直接關系到游樂設施的正常運行和乘客的生命安全。本文以大型游樂設施中的焊縫為例，對焊縫部位的應力，分別按照力學理論計算和有限元分析計算，給出對接焊縫和角焊縫的計算公式和校核評價方法，并對有限元計算建模時，是否考慮焊縫材料進行了分析比較。研究表明，焊縫的校核計算應該按照名義計算應力進行校核評價，不宜用有限元法去校核評價的游樂設施焊縫。研究方法和結果為大型游樂設施結構件焊縫的校核計算提供參考性建議和依據。

對接焊縫；有限元；名義計算應力；應力集中；大型游樂設施

游樂設施金屬結構所采用的連接方式主要為螺栓緊固和焊接[1]，游樂設施很多零部件都是通過焊接來進行連接緊固的[2]。隨著游樂設施朝著更快、更高的方向發展，其結構焊縫主要承受交變動載荷，從焊縫連接構造和強度計算特點出發，游樂設施中的焊縫分為對接焊縫和角焊縫。對于T型接頭和角接接頭，對接焊縫與角焊縫的主要區別在于焊縫是否能夠在板邊整個厚度上連續焊透，焊透了為對接焊縫，如不焊透則為角焊縫[3]。《游樂設施安全技術監察規程》[4]規定：角焊縫承受動載荷的，應采用全焊透結構。由于游樂設施主要承受動載荷，因此游樂設施中的重要焊縫，不管是對接焊縫還是角焊縫，大多采取全焊透焊縫。

本文以游樂設施的對接焊縫和角焊縫為例，分別利用應力計算公式和有限元軟件分析計算焊縫部位的應力，為游樂設施結構焊縫的計算提供參考。

1 對接焊縫強度理論算例

由文獻[4]可知，對接焊縫的計算要求為：承受軸向拉力或壓力的對接焊縫，應計算其縱向拉、壓應力；承受彎矩和剪力聯合作用的對接焊縫，應計算其危險點的最大正應力和最大剪切應力；對角焊縫的計算要求為：角焊縫應計算其抗剪強度，當角焊縫受復合內力作用時，應計算出合應力。根據規范要求按照破斷拉力與最大計算應力的比值來校核焊縫。

為了說明焊縫理論計算和有限元計算的區別，下面舉例說明。

圖1中節點板和預埋鋼板間的T型對接焊縫。承受拉力作用，焊縫等級為Ⅰ級，偏心力＝120000 N，鋼材為Q235B，手工焊，焊條為E43型。按照文獻[8]計算焊縫應力值。并結合文獻[4]對焊縫進行校核評價。

圖1 焊縫受力示意圖

首先對力在焊縫部位進行分解，分解為水平方向的拉力和豎直方向的剪切力[5]：

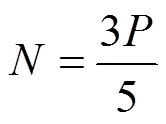
式中：為水平方向的拉力，N；為豎直方向的剪切力，N。

計算得：＝72000；＝96000。

由于水平拉力未通過焊縫的形心，在焊縫部位產生一個附加彎矩[5]：

＝（3）

式中：為彎矩，N·mm；為拉力與焊縫的形心的距離，mm，＝20。

計算得：＝1440000。

對接焊縫，根據構件截面計算焊縫應力[6]。焊縫下端點最危險，該點各項應力為[5]：

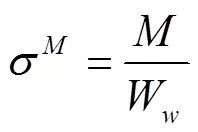
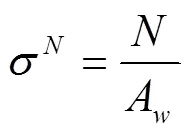
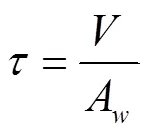
則：

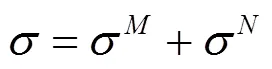
理論計算焊縫的合應力為[5]：

由文獻[4]可知，對接焊縫按照最大正應力和最大剪應力分別評價，焊縫等級為Ⅰ焊縫，則：

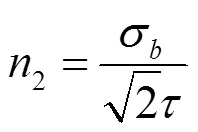
焊縫的分析結果表明，焊縫合應力的安全系數小于5.0，不滿足安全規范要求。

2 對接焊縫有限元計算

由圖1構建精細化的三維模型，構建兩種模型，其幾何形狀分別見圖2，圖2（a）不考慮焊縫材料，圖2（b）考慮焊縫材料，采用實體單元進行分析比較。

圖2 幾何模型

在載荷和約束不變的情況下，通過不同的網格尺寸，計算零件的最大應力值。為了比較不同模型和網格尺寸對結果的影響，分別對無圓角和有圓角的模型在主體網格單元尺寸分別是10 mm、5 mm和3 mm等算例進行計算。通過不考慮焊縫材料和考慮焊縫材料，即無圓角和有圓角在不同網格的計算結果如圖3所示。

計算結果曲線圖如圖4所示。

對計算結果進行匯總，結果如表1所示。

由圖4可知，不考慮焊縫材料（不帶圓角），由于連接區域應力奇異，不收斂，所以網格越細應力就會越大（如果網格持續加密，應力值會持續增大），有限元得到的結果是不可信的，會使焊縫部位的應力計算結果偏大；考慮焊縫材料（帶圓角）的計算結果趨于穩定，結果可接受。

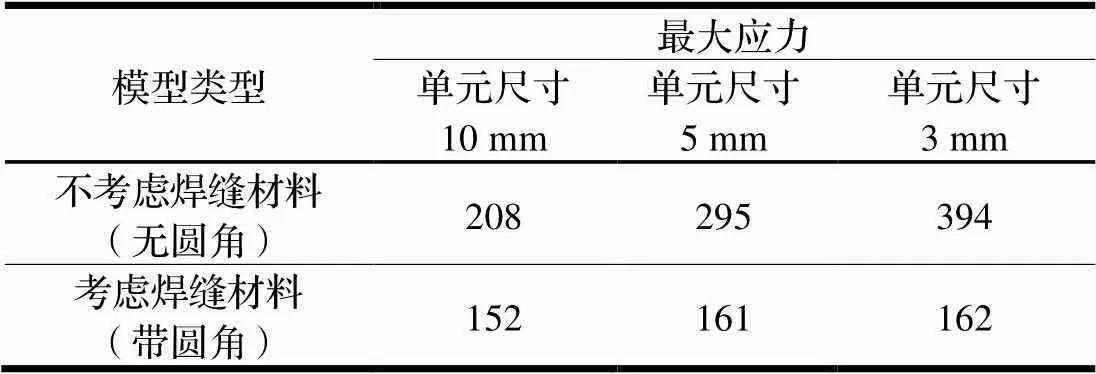
表1 計算結果匯總（單位：MPa）

在游樂設施有限元設計計算中，國內大多廠家常常將焊縫簡化并忽略，從以上計算可以看出，不考慮焊縫材料，會使焊縫附近的應力計算結果偏大，出現虛假的應力，即應力奇異。事實證明，對焊縫進行簡化或忽略會造成計算結果的偏差，對游樂設施中重要部位的焊接，如果要知道焊縫部位的實際應力值，要將焊縫的結構建立出來，把模型做精細，該倒角的就倒角，把有過渡的部份都做出來再做分析。

3 應力集中的影響

由以上分析可知，焊縫部位實際應力約為159 MPa，而名義計算應力的值101 MPa，仿真計算的結果和理論計算的結果差異很大。局部焊縫有應力偏大的情況，這是受到應力集中的影響。因為名義計算應力沒有考慮應力集中的影響，所以仿真結果和名義計算應力有大的差異。焊縫部位的應力集中系數為159/101＝1.6。

接工藝過程對接頭質量的影響因素很多，因此，若要按實際應力狀態精確計算焊縫的強度是很困難的，目前焊接接頭的靜強度計算都是在一定的假設條件下進行的，由文獻[3]可得焊接接頭靜強度計算的假設如下：

（1）略去焊接殘余應力及焊縫根部和焊趾區的應力集中對焊接接頭強度的影響；

（2）對接焊縫的計算厚度按被連接的兩板中較薄板的厚度計算，不考慮焊縫的增高；

（3）接頭的工作應力是均布的，以平均應力計算[2]。

圖4 不同模型計算結果曲線圖

由以上規定可知，焊縫的計算時不考慮應力集中的影響，而有限元計算，不可避免的加入了應力集中因素。現有的焊縫評價標準沒有考慮焊縫部位的應力集中，采用較大的安全系數，來涵蓋應力集中、殘余應力等因素的影響，同時，通常游樂設施結構復雜，關鍵焊縫較多，若全部通過構建焊縫材料，模型規模太大。

因此有限元計算結果不適合現有的焊縫評價規范標準，這也是為什么同一部位，有限元計算結果偏大（包含應力集中影響），而焊縫的名義計算應力結果偏小的原因（忽略應力集中影響）。然而大多數廠家在進行游樂設施的焊縫計算時，由于沒有構建焊縫材料模型，焊縫部位的應力過大，導致焊縫結果不符合規范要求，于是常見取距離焊縫一定距離（焊縫高度）的節點值，作為焊縫應力去評價，這種評價方法是不嚴謹的。

4 節點值作為焊縫應力是否合理

一般在靜載情況下，焊材的強度會遠遠高出母材，文獻[4]按照等強度理論做分析是一種保守的做法，游樂設施焊縫強度計算的正確做法是：按照理論計算公式，根據焊接類型、熔深、焊縫大小，焊縫長度等，得出焊縫計算應力（不考慮應力集中影響），再去評價焊縫[7]。

然而在一些企業的游樂設施計算書中，經常會遇到取距離焊縫一定距離（焊縫高度）的節點值作為焊縫應力去評價，為了說明節點值作為焊縫應力值是否合理，以第1節對接焊縫強度理論算例的例子進行說明，在通過最大應力值的有限元模型上建立一條路徑，如圖5所示。

圖5 應力線性化位置圖

由圖6可知，距離最大應力值一定距離上，應力值急劇變化，從394 MPa瞬間降到0，距焊縫12 mm的節點應力值為84 MPa，距焊縫15 mm的節點應力值73 MPa，則對應的安全系數（Q235B的抗拉強度為375 MPa）分別為4.5和5.1，這樣同一條焊縫就可得出兩種評價結論（節點位置僅差3 mm，焊縫安全系數是否滿足要求的臨界值為5.0）。

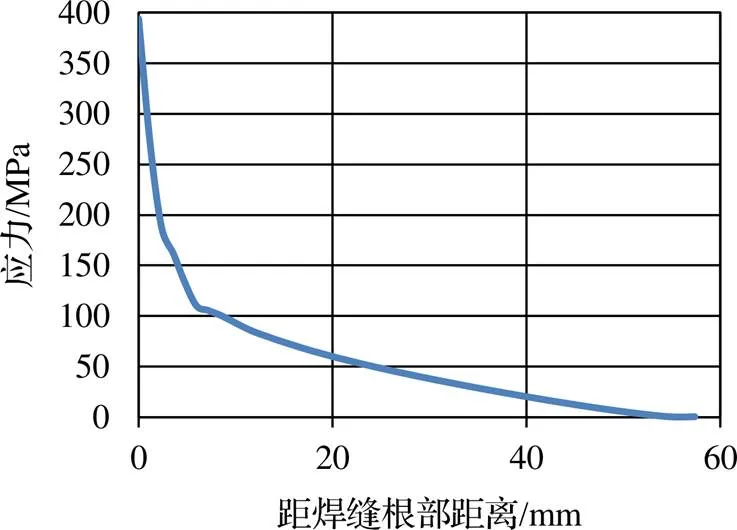
圖6 應力線性化曲線

在距離焊縫一定位置上（全憑工程師手動操作）取值，可取的范圍很大，稍微移動一點距離，應力值就相差很大，焊縫的計算是嚴謹的，這樣取值稍微有偏差，可能會得出完全不同的評價結果。因此，忽略焊縫材料的影響，取距離焊縫一定距離的節點值作為焊縫應力值是不確定的，也是不科學、不合理的。

5 角焊縫計算

正應力會使材料拉伸或壓縮，剪應力會使材料發生剪切變形。由文獻[8]得：

如果存在合應力，則角焊縫的計算公式為（游樂設施按照焊縫承受動載荷計算）：

焊接接頭強度計算的假設為[2]：

（1）正面角焊縫與側面角焊縫的強度沒有差別；

（2）角焊縫是在切應力的作用下破壞的，按切應力計算強度；

（3）角焊縫的破斷面（計算斷面）在角焊縫截面的最小高度上；

（4）加厚高和少量的熔深對接頭的強度沒有影響。

角焊縫連接的破壞形式和焊縫截面應力分布較復雜，為簡化計算，假定角焊縫發生剪切破壞，切應力沿焊縫長度方向均勻分布[5]。工程實踐證明，按名義計算剪應力來計算角焊縫既可靠又簡便[3]。

綜上可知，角焊縫雖可能承受各種應力，但最后都是以等效剪切應力去評價校核。但游樂設施對角焊縫的校核評價，不采用鋼結構標準中給出的強度設計值，而是采用安全系數法校核評價，即Ⅰ級和Ⅱ級焊縫的安全系數≥5[4]。

6 結論

焊縫從原理上說不是一個零件，是兩個零件融合在一起的一個特殊狀態區，受到殘余應力、應力集中等因素的影響，研究焊接殘余應力，必須模擬焊縫熔池金屬和母材金屬從熔化到凝固、冷卻為常溫的全過程，而各種焊縫的約束條件又是不一樣的。熔化、冷卻、凝固、繼續冷卻整個熱力學過程的各項參數難以確定，因此理論計算中忽略了焊縫的殘余應力、缺口應力集中等效應，按照相應的標準規范，理論計算焊縫，并進行校核評價[9]。

正如以上所述，焊縫的應力狀態是相當復雜的，對接焊縫與角焊縫的應力狀態又是不同的，若要對各種受力類型的焊縫進行精確的計算是相當困難的[10]。因此，對游樂設施焊縫的計算應按照以下原則進行：

（1）焊縫的校核計算應該按照名義計算應力計算，并按照文獻[4]進行校核評價；

（2）有限元計算結果考慮了應力集中的影響，不能按照現有的焊縫評價標準體系去評價焊縫；

（3）取距離焊縫一定距離的節點應力，存在很大的不確定性，且沒有相應的理論支撐，不能作為焊縫應力去評價；

（4）角焊縫的名義計算應力僅考慮剪切應力，當受復合內力作用時，按照剪切應力的合應力去校核焊縫，焊縫計算的破斷應力由角焊縫的抗剪條件確定[11]。

有限元應力分析僅有計算云圖和計算結果是遠遠不夠的，分析者必須具有判斷計算結果準確性的能力，除了具有熟練的軟件應用能力，還需掌握力學理論和有限元理論。

[1]趙九峰. 基于ANSYS Workbench自控飛機回轉機構驅動功率的計算及電機選型[J]. 機械，2019（4）：30-33.

[2]王文先，王東坡，齊芳娟，等. 焊接結構[M]. 北京：化學工業出版社，2012.

[3]董達善. 起重機械金屬結構[M]. 上海：上海交通大學出版社，2011.

[4]GB 8408－2018，大型游樂設施安全規范[S].

[5]范欽珊. 工程力學(靜力學和材料力學)[M].北京：高等教育出版社，2007.

[6]徐格寧. 機械裝備金屬結構設計[M]. 北京：機械工業出版社，2010.

[7]崔玉淼. T形接頭的焊縫靜載強度計算公式推導及應用[J]. 焊接技術，2015（7）：11-13.

[8]GB 50017－2017，鋼結構設計標準[S].

[9]曹華，李自梁，劉美紅，等. 蝸殼-座環連接焊縫焊接殘余應力的測試與分析[J]. 熱加工工藝，2019（5）：203-205.

[10]陳太軍，賴傳理，杜顯祿，等. 帶堆焊層和復合層角焊縫超聲波檢測應用[J]. 機械，2018（10）：49-55.[11]宋偉科，陽先波. 大型游樂設施結構件焊縫設計計算研究[J].中國特種設備安全，2016（12）：7-10.

Strength Check Calculation and Analysis on Welding of Large-Scale Amusement Device

ZHAO Jiufeng

( Special Equipment Safety Inspection and Research Institute of Henan Province,Zhengzhou 450000, China )

Welding is the main connection method of large-scale amusement device. The weld design calculation is directly related to the normal operation of the equipment and the safety of the passengers. Taking the welds of large-scale amusement device as an example in this paper, the stress of the weld is calculated according to theory calculation and finite element analysis. The calculation formulas and evaluation methods of butt welds and fillet welds are given, and a comparison analysis is made on whether or not to consider the weld materials when modeling. The research shows that the calculation of weld should be evaluated according to the nominal calculated stress. it is not appropriate to use the finite element method to check the welds of amusement device. The research methods and results provide the reference recommendations and reference for the design and calculation of welds of amusement device.

butt welding；finite element analysis；nominal calculated stress；stress concentration；large-scale amusement device

TS952.82

A

10.3969/j.issn.1006-0316.2020.04.005

1006－0316 (2020) 04－0027－07

2019－06－14

趙九峰（1981－），男，河南平頂山人，碩士研究生，工程師，主要從事游樂設備設計計算、特種設備結構仿真與載荷響應研究工作。