自適應爆炸半徑的改進煙花算法

趙志剛，李智梅，莫海淼，曾 敏，溫 泰

(廣西大學 計算機與電子信息學院，廣西 南寧 530004)

0 引 言

Tan等[1]提出了煙花算法(fireworks algorithm，FWA)，該算法收斂速度快，易于實現，且具有爆發性、多樣性和隨機性等特點，目前被廣泛應用于網絡定位[2]、JSP問題求解[3]、投資組合優化問題[4]、聚類[5]等多個領域。煙花算法在應用到某些實際的過程中表現力不從心，因此眾多學者對煙花算法進行改進，主要是對FWA算法的算子分析及改進以及與其它啟發式算法結合成混合算法[6]。Barraza等[7]基于模糊邏輯，對爆炸火花數目以及爆炸振幅進行調整，提高了煙花算法的性能。Zhang等[8]提出了BBO-FWA算法，將生物地理學優化算法的遷移算子引入煙花算法，表現出了較強勘探能力。Babu等[9]基于粒子群算法和遺傳算法的改進煙花算法來精確識別光伏(PV)模塊的雙二極管模型未知參數，有效地解決了這一建模問題。Bao等[10]提出了一種改進的混沌煙花算法，在求解多目標JSP問題上具有較高的準確性和魯棒性。Xue等[11]提出了一種自適應煙花算法(SaFWA)來優化分類模型，利用4種候選解生成策略(CSGSS)來提高解的多樣性。Yan等[12]提出了具有線性降維策略的動態搜索煙花算法(ld-dynFWA)，提高了算法的效平衡率和穩定性，并將其應用于求解條件非線性最優攝動CNOP問題。

以上方法沒有考慮到被丟棄的爆炸火花信息利用的問題。為了更好地提高煙花算法的性能，利用被丟棄的爆炸火花的信息，改進爆炸機制，提出了一種具有自適應學習改進煙花算法。該算法從信息利用、自適應步長及種群多樣性的增加3個角度對FWA算法進行改進，以爆炸火花的數目為分種群依據，利用爆炸火花的位置信息來構建爆炸半徑，并對全局最優進行高斯變異。為了對改進煙花算法進行性能測試實驗，選擇10個比較常見的基準測試函數以及幾種經典的群智能優化算法(如標準粒子群算法PSO、帶高斯擾動的粒子群算法GPSO、蝙蝠算法BA、煙花算法FWA、自適應煙花算法AFWA、增強煙花算法EFWA)進行對照并分析。

1 煙花算法

煙花算法是根據煙花在夜空中爆炸的現象而提出的一種新型群智能優化算法，該算法主要包括四大部分：爆炸算子(爆炸強度、爆炸幅度和位移操作)、變異算子、映射規則和選擇策略。

1.1 爆炸強度

煙花爆炸時，煙花種群的每個煙花都會生成相應的爆炸火花子種群。適應度值越好的煙花爆炸強度越大，爆炸火花的數量就越多；相反，爆炸強度越小，爆炸火花的數量就越少[13]。爆炸強度的計算如式(1)所示

(1)

式中：Si表示第i個煙花產生爆炸火花的數量；m是限制爆炸火花數量的常量；Ymax是煙花中最差適應度值的個體；f(xi)是第i個煙花的目標函數的適應度值；θ是極小的機器數；pop是指煙花種群數目。

使用式(2)來控制爆炸火花數量的大小

(2)

其中，round()為四舍五入的取整函數；α和β均為常數變量。

1.2 映射規則

在尋優的過程中，需對越界的煙花個體進行如下越界處理

(3)

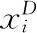
1.3 選擇策略

FWA算法是基于歐氏距離來計算任意兩個煙花個體間的距離，計算公式如下

(4)

其中，d(xi,xj) 是任意兩個煙花xi與xj間的歐式距離；R(xi) 是煙花個體xi到其它個體的距離的總和；l∈K是第l個位置屬于集合K；K表示煙花、爆炸算子和變異算子產生火花的煙花種群位置集合。

在進行下一代煙花種群選擇時，其策略是采用輪盤賭的方式，與其它個體具有更遠距離的煙花個體具有更大的可能性被選擇，每個個體被選中的概率用p(xi)表示，即

(5)

1.4 變異算子

高斯變異是對煙花隨機選擇若干個維度進行操作，該操作具體為

(6)

2 改進的煙花算法

在FWA算法中，由1.3小節選擇策略可知，沒有被選中為下一代煙花的爆炸火花則完全被丟棄，這浪費了被丟棄的爆炸火花的信息。針對這一點，引入sparkpBest來表示在尋優過程中每個煙花所產生的最優爆炸火花個體的集合，并將其和最優煙花個體gBest來構造新的爆炸半徑，同時對gBest進行變異算子操作進一步增加種群的多樣性，避免煙花算法有“早熟”的情況。

2.1 新的位移操作和爆炸半徑

位移操作是對煙花的每一維度進行操作，在FWA算法中，由于一個煙花爆炸時在每個維度上產生了相同位移偏移的爆炸火花，煙花算法的多樣性有所降低。改進的煙花算法在煙花個體產生爆炸火花的過程中，因為使用了煙花的位置信息來構造新的爆炸半徑，能夠自適應地調整步長，這就使得在各個維度上可以采取不同的位移偏移來進行位移操作，其更新公式如下

xlast(l)=x(i)+r*EA(i)

(7)

其中，l=1,2,…,Si；x(i) 是第i個煙花未爆炸前的位置，xlast(l)是第i個煙花爆炸后對應子種群的第l個爆炸火花的位置；r是在[0,1]內的隨機數，服從均勻分布；EA(i) 是第i個煙花爆炸產生的火花相對原始煙花的范圍(煙花的爆炸半徑)。

爆炸半徑是指煙花個體發生爆炸之后所發生的位移，通過FWA算法中爆炸半徑的計算公式可得，煙花的爆炸半徑是利用煙花的適應度值來獲取，這是不科學的，這是因為對于多維空間問題而言，可能會存在多個煙花的適應度值相等而位置不一樣的情況，即無法判斷實際的位置，因此改用位置信息。另外，根據式(4)，沒有被選中為下一代煙花的爆炸火花則完全被丟棄，這浪費了被丟棄的爆炸火花的信息。針對這一點，引入sparkpBest來表示在尋優過程中每個煙花所產生的最優爆炸火花個體的集合，并將其和最優煙花個體gBest來構造新的爆炸半徑，以爆炸火花數目作為分種群的依據，將煙花種群分為兩類，爆炸強度小于平均爆炸強度的煙花為次好煙花，次好煙花向sparkpBest靠攏，即擴大搜索范圍進行全局搜索；爆炸強度大于或者等于平均爆炸強度的煙花為優質煙花，優質煙花向此時最優煙花位置靠攏，即向當前種群最優gBest學習，在gBest附近進行詳細的局部搜索提高收斂速度。

新的爆炸半徑計算公式具如下所示

(8)

其中，sparkpBest(i)是第i個煙花產生的爆炸火花子種群中的個體最優；AvgS是此時所有爆炸火花的均值，即

(9)

2.2 全局最優個體的高斯變異

式(6)是隨機選擇幾個維度來進行高斯變異，在此基礎上，再對全局最優個體gBest進行高斯變異，即對該最優個體的所有維度進行變異算子操作，以便能夠增加煙花算法中種群的多樣性，使得改進煙花算法的全局搜索能力得到增強，提高其運算結果，具體操作如下

gBest=gBest*(N(0,1)+1)

(10)

其中，N(0,1) 是服從均值為0，方差為1的高斯分布函數。

2.3 ARFWA算法

綜上所述，提出了一種改進的煙花算法，即自適應爆炸半徑的改進煙花算法(improved fireworks algorithm with adaptive explosion radius，ARFWA)。ARFWA算法的偽代碼如下：

步驟1 初始化煙花種群x，全局最優gBest，每個煙花所產生的最優爆炸火花個體的集合sparkpBest；

步驟2 獲取每一個煙花的適應度值；

步驟3 將gBest狀態更新；

步驟4 通過式(10)和式(3)對gBest前后進行高斯變異和越界處理操作；

步驟5 通過式(1)來計算煙花的爆炸強度；

步驟6 通過式(8)和式(9)來計算每一個煙花的爆炸半徑；

步驟7 通過式(7)來進行位移操作，并更新sparkpBest；

步驟8 使用式(6)產生高斯火花；

步驟9 根據1.3小節的選擇策略來選擇下一代煙花；

步驟10 不斷執行步驟2～步驟9，符合終止條件時就停止操作。

3 仿真實驗

3.1 實驗測試函數

為了評估改進的煙花算法在函數優化的有效性，實驗選取了10個基準測試函數進行算法對比，如表1所示，包含其域，最優值以及維度信息。

表1 基準測試函數

3.2 參數設置

ARFWA算法和FWA算法的參數設置均參見文獻[1]，SPSO算法參見文獻[14]，GPSO算法參見文獻[15]，BA算法參見文獻[16]，自適應煙花算法參見文獻[17]，增強煙花算法參見文獻[18]。為了客觀對比，7種算法的種群大小均為10，尋優精度設置為10-5。本次實驗運行次數設置為100次，最大迭代次數設置為1000次。實驗平臺是Matlab 2016Ra，Inter(R) Xeon(R) CPU E5-1620 v3 @3.5 GHz,window10操作系統。

3.3 收斂性能分析

對表1的函數進行仿真實驗，得到各個函數的求解質量，如表2所示(worst是最差值、best是最佳值、avg是平均值、std是方差值)，avg的平均排名結果見表3，尋優成功率用SR表示，見表4，各算法的尋優進化曲線圖展示如圖1至圖10所示。為了方便對比分析，f7的適應度值是負數沒有取對數，保持原始值不變，剩余函數的曲線圖中縱坐標log10(Fitness)代表其適應度值均取對數log10。各函數(除了f1、f3、f4和f9外)的演化曲線出現部分重疊的情況。

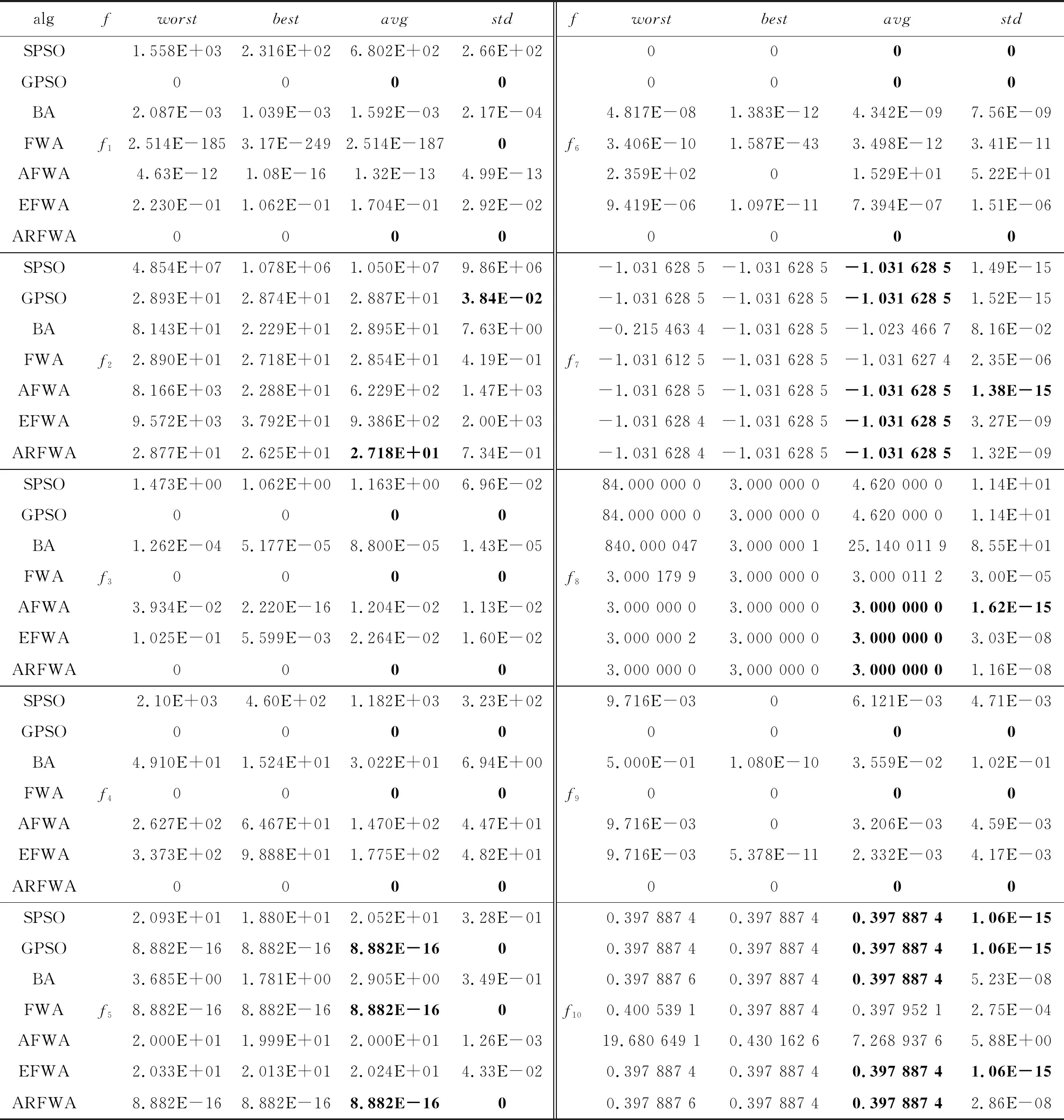
表2 各個函數求解質量

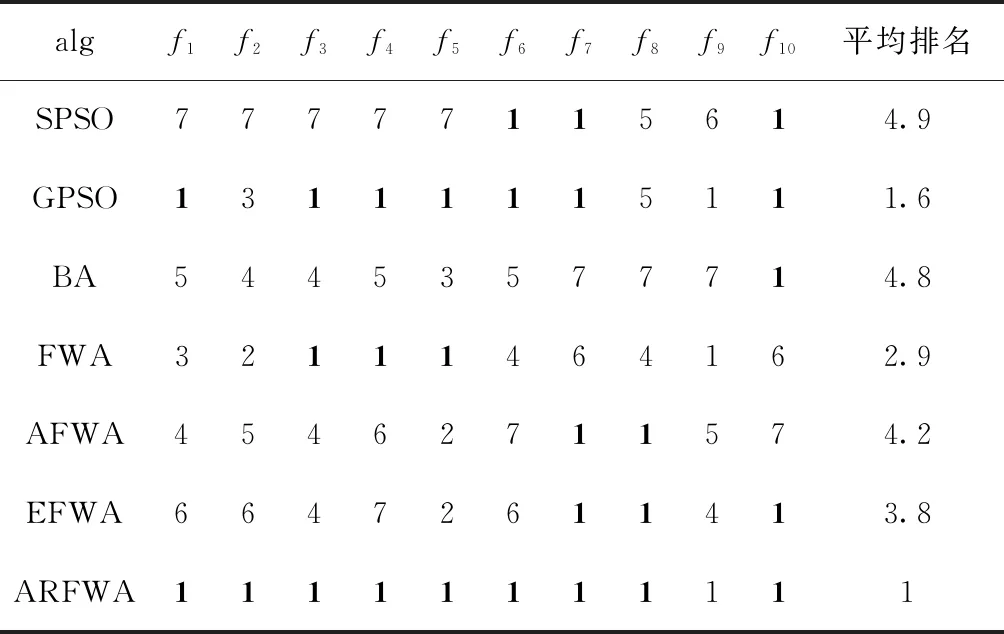
表3 在測試函數上的平均排名

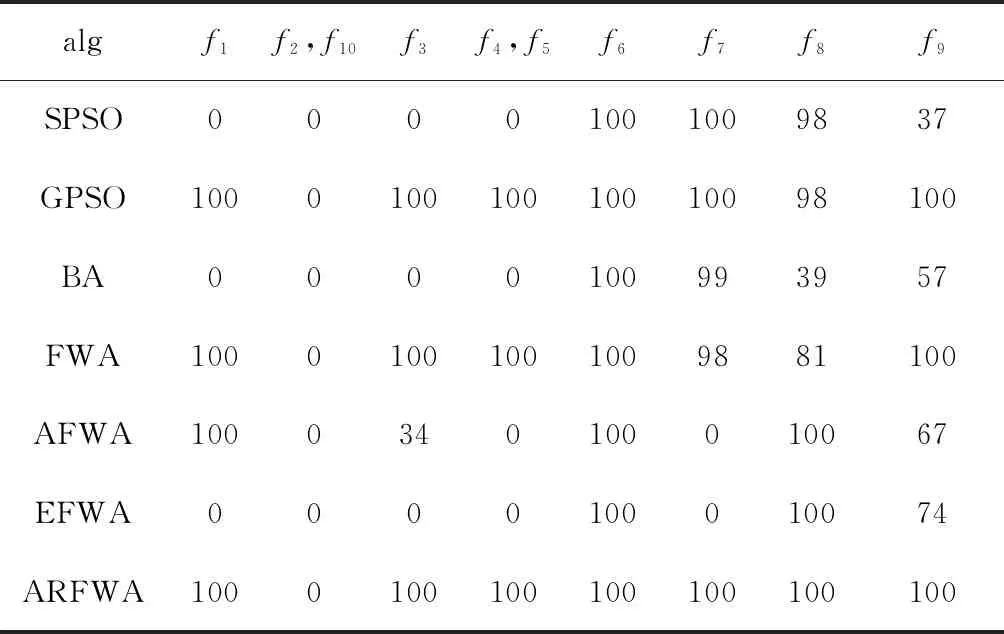
表4 f1～f10：7種算法尋優成功率SR/%

觀察f1、f3、f4、f6和f9函數尋優進化曲線圖(圖1、圖3、圖4、圖6和圖9)可知，當算法迭代的次數是一樣時，ARFWA表現出的收斂性能(收斂速度和收斂精度)明顯比其它對比算法更出眾。由表2對應函數的結果avg可得，ARFWA與GPSO具有一樣的avg，且比其它對比算法更優。

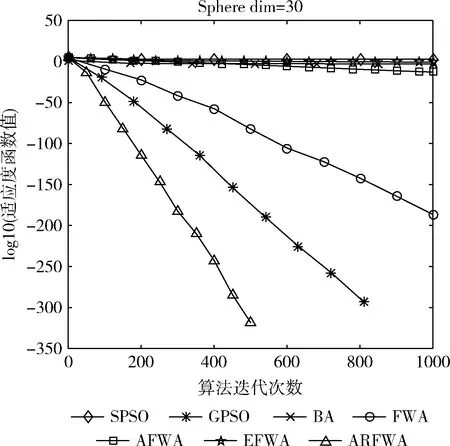
圖1 f1尋優進化曲線

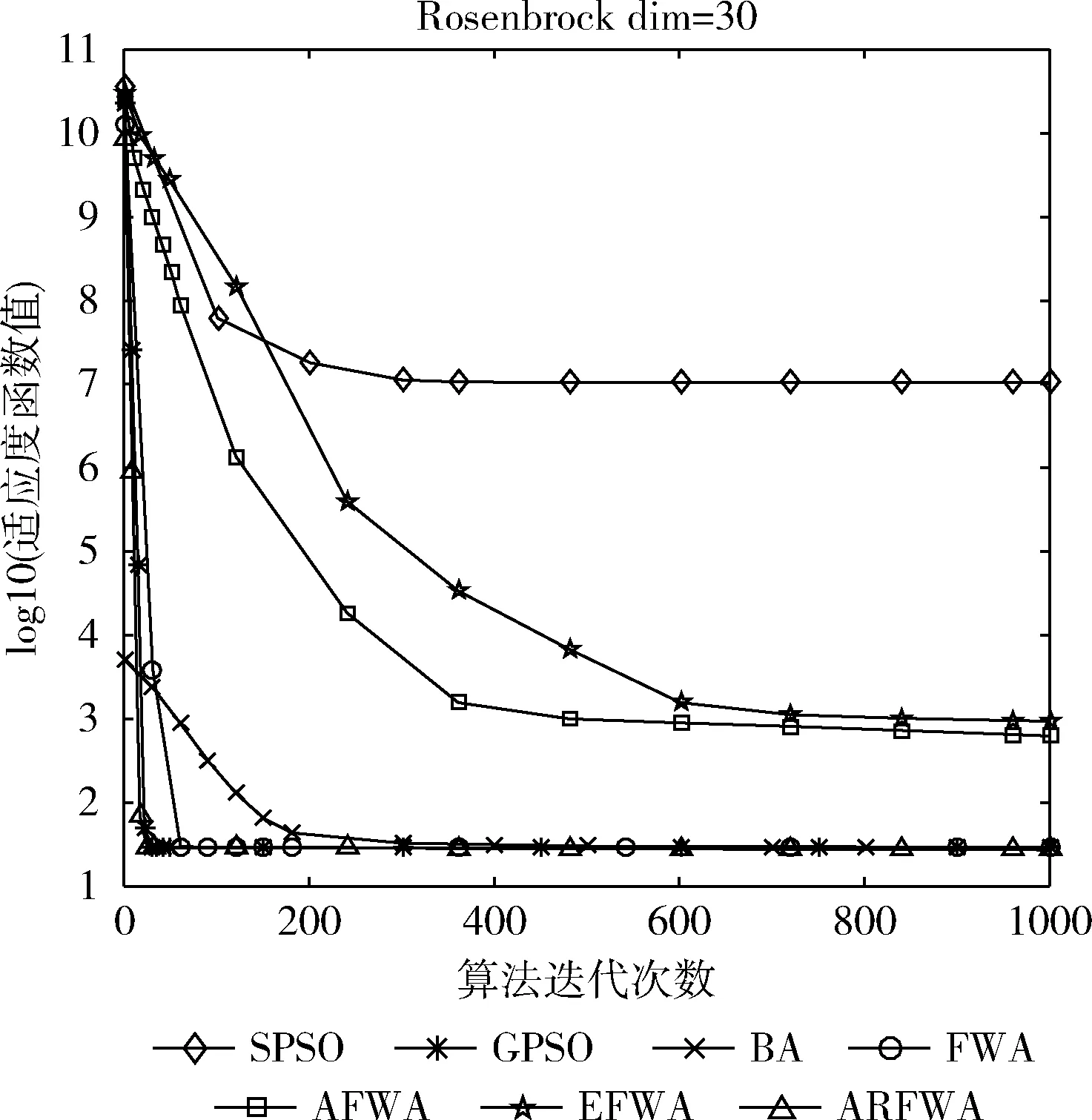
圖2 f2尋優進化曲線

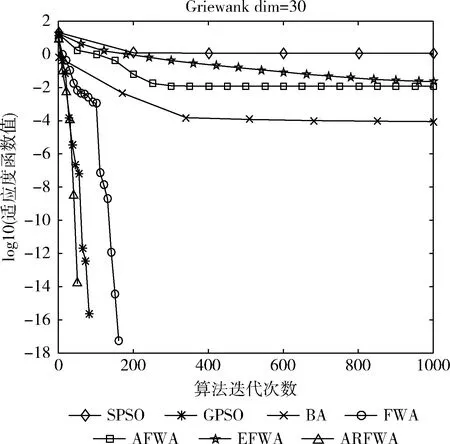
圖3 f3尋優進化曲線

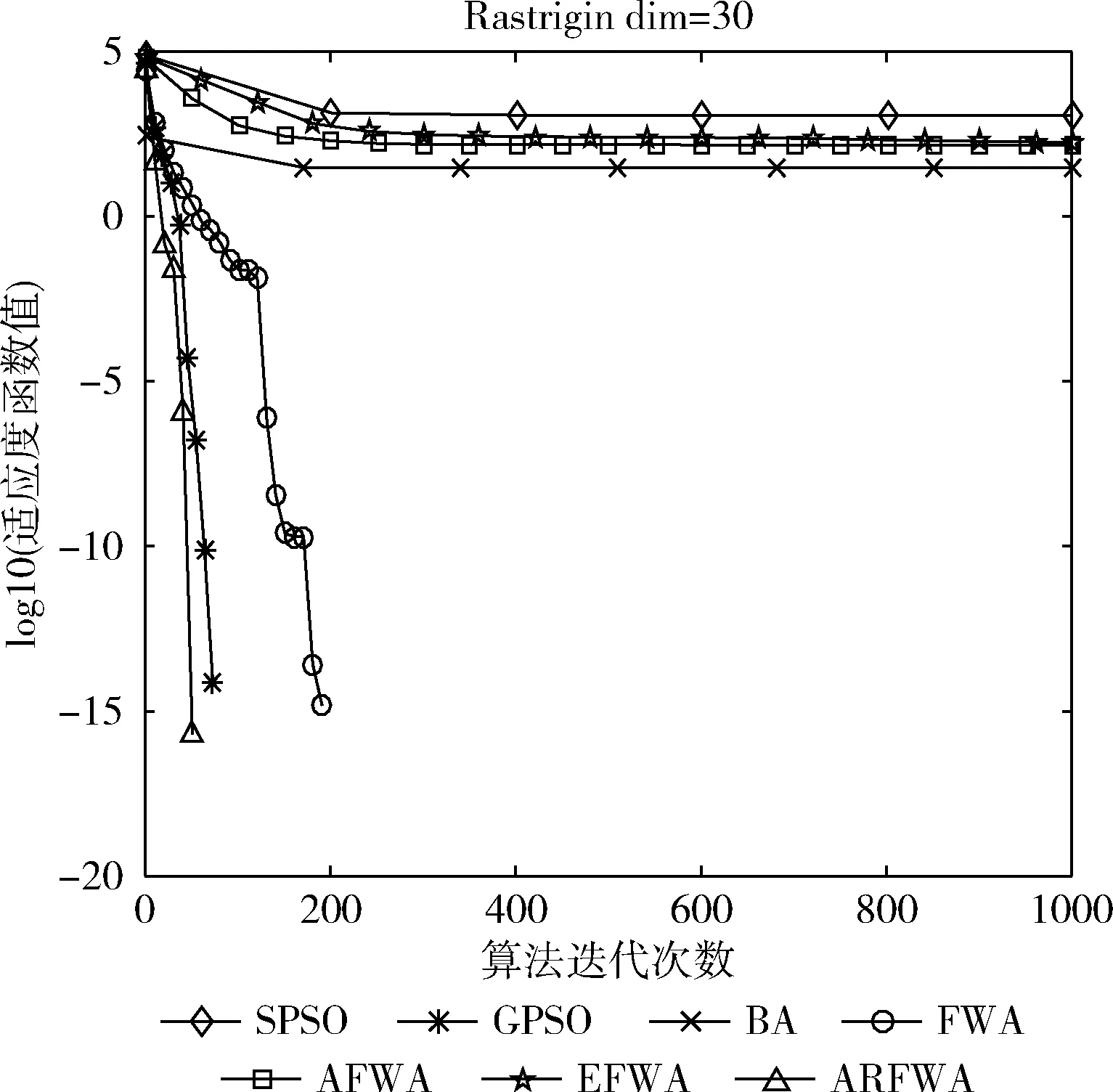
圖4 f4尋優進化曲線

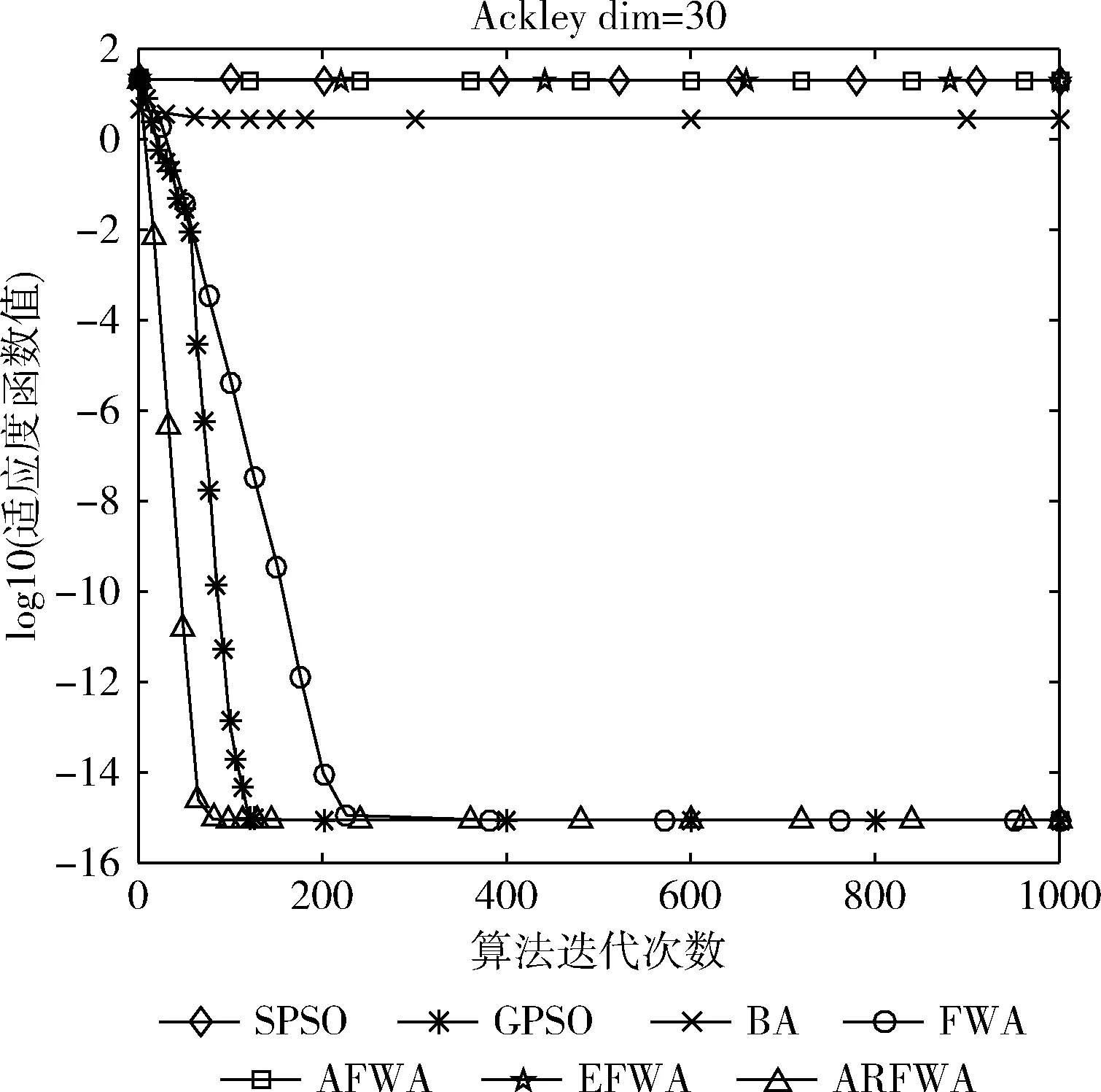
圖5 f5尋優進化曲線

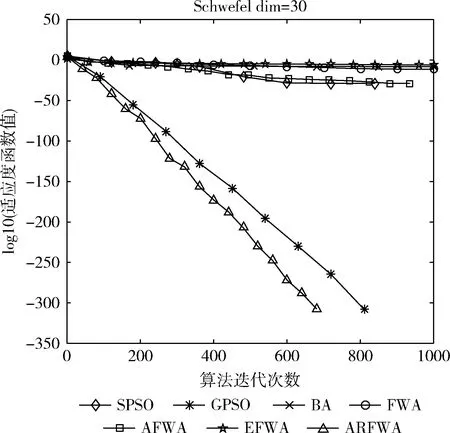
圖6 f6尋優進化曲線

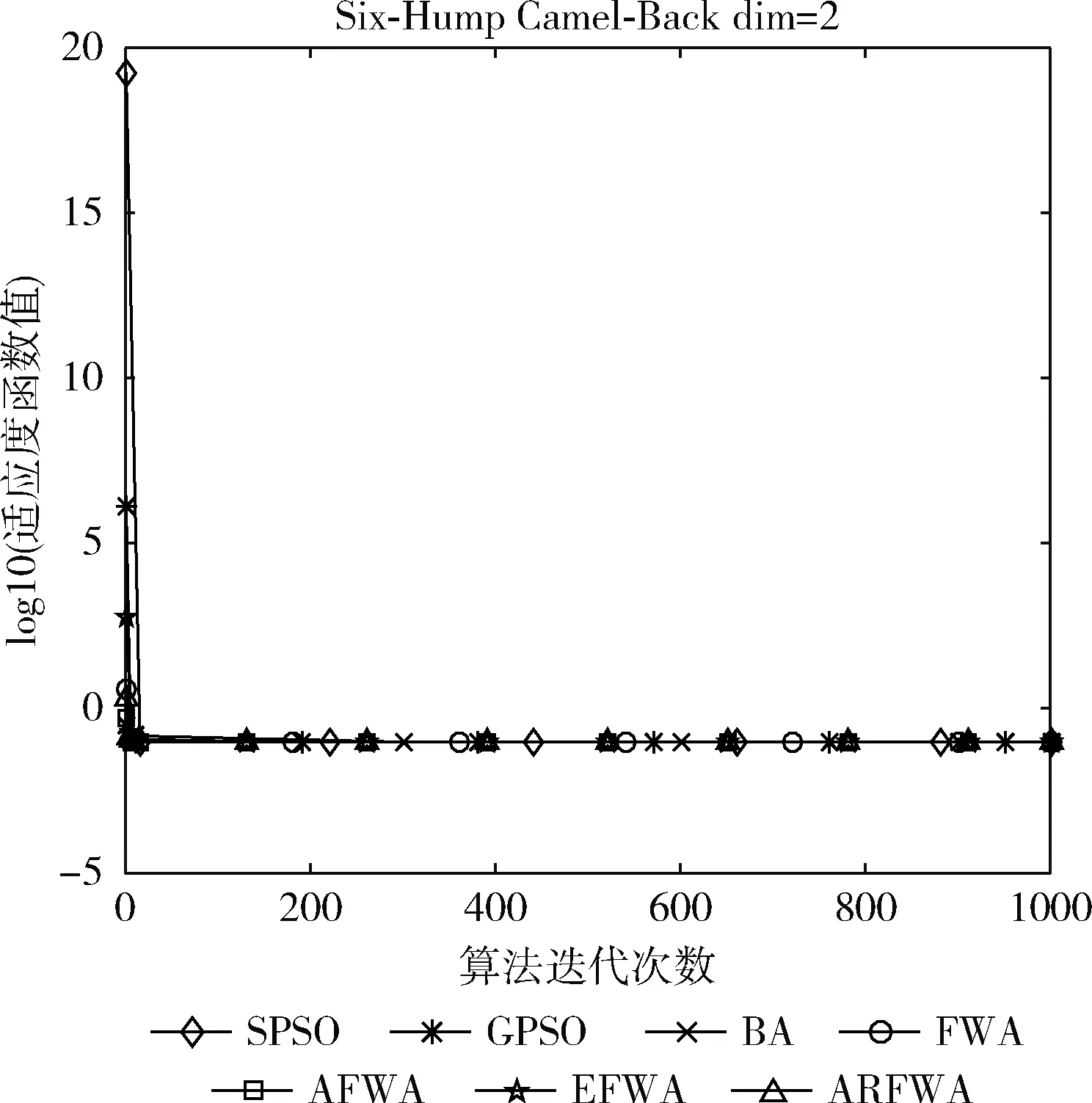
圖7 f7尋優進化曲線

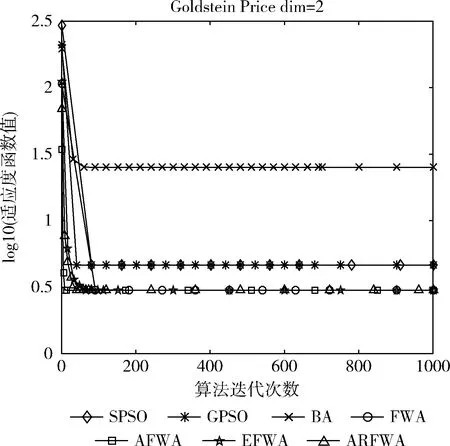
圖8 f8尋優進化曲線

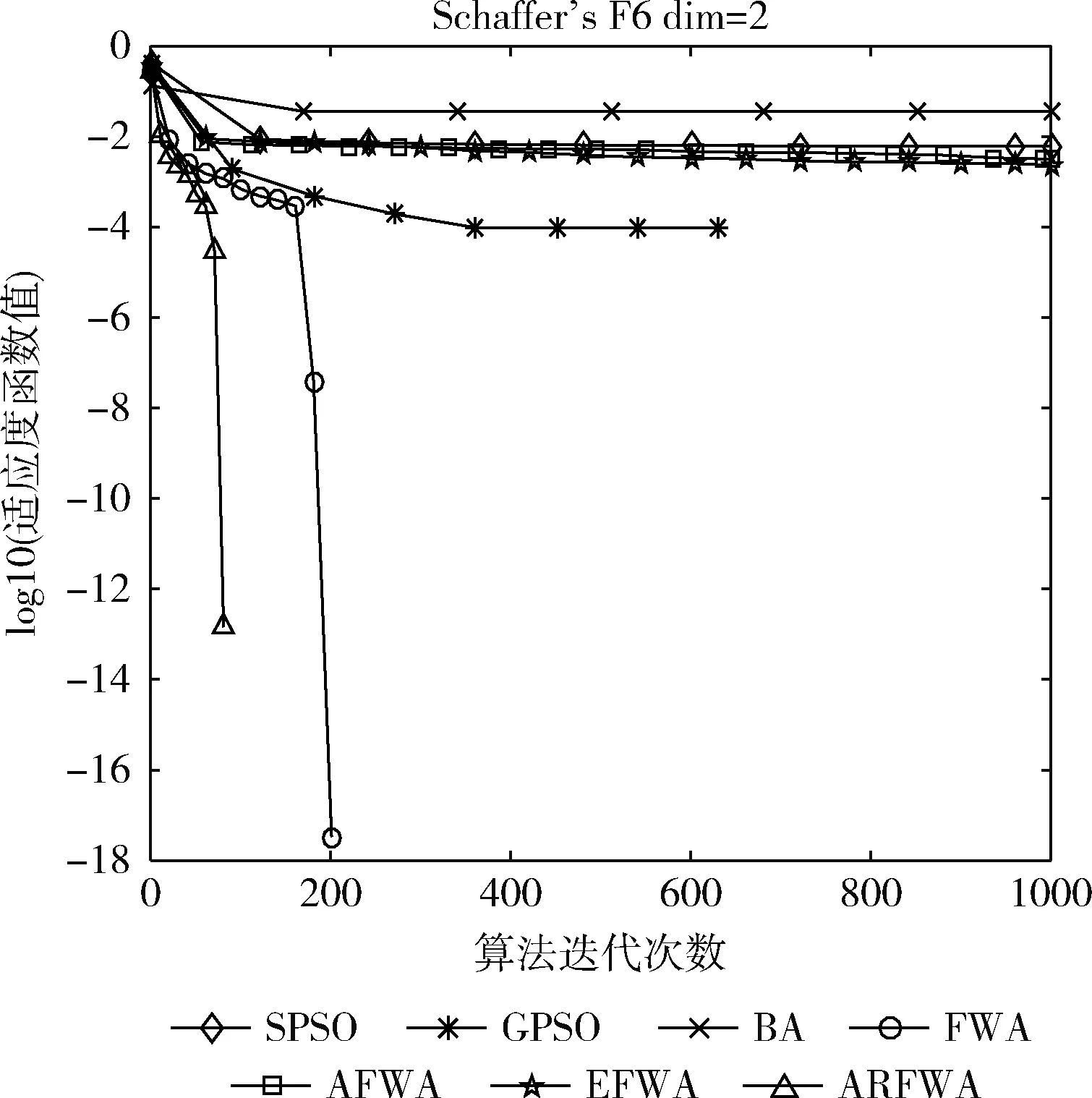
圖9 f9尋優進化曲線

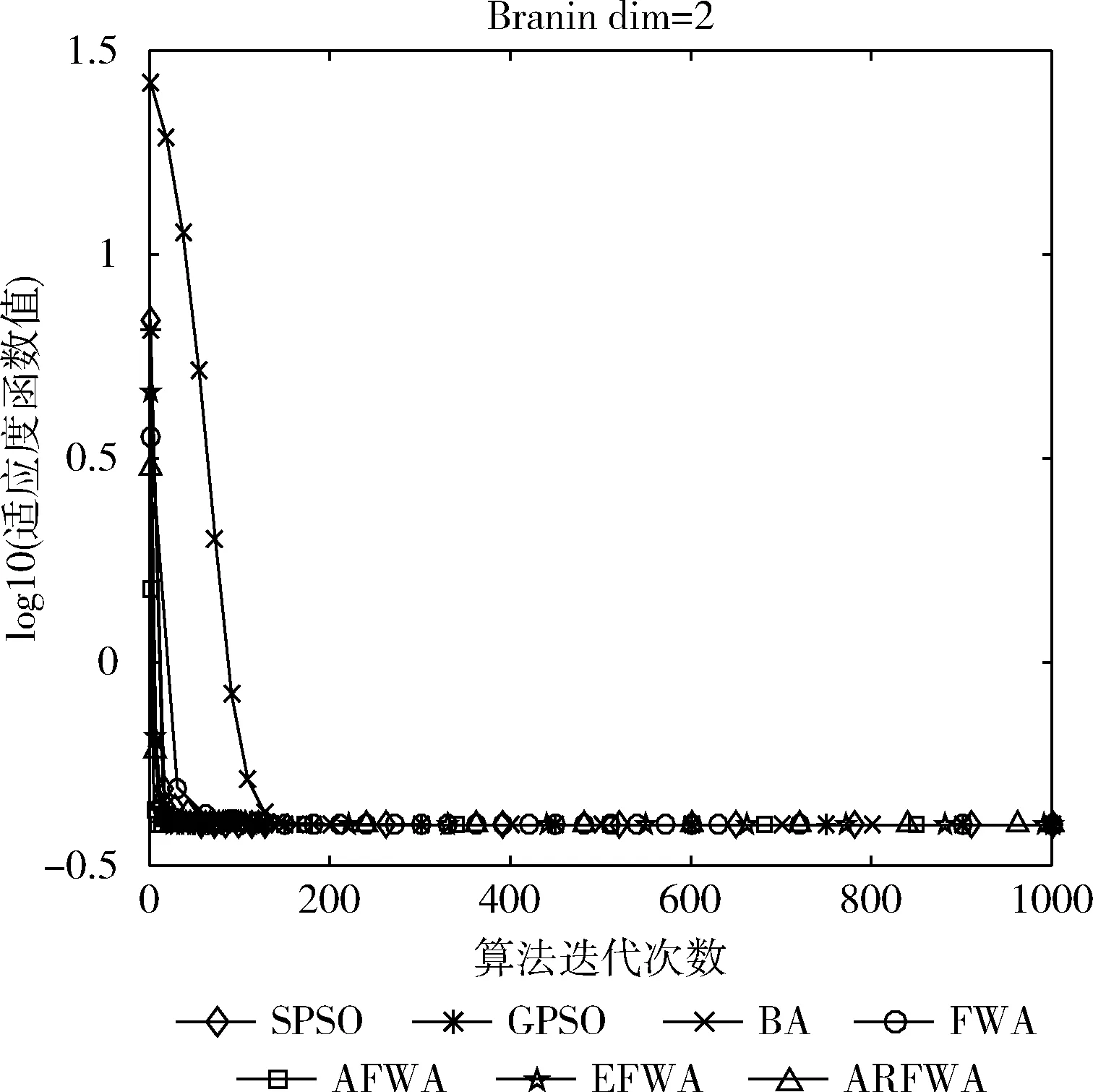
圖10 f10尋優進化曲線

觀察f2、f5函數尋優進化曲線圖(圖2和圖5)可知，在算法迭代前期，迭代的次數一樣時，ARFWA表現出的收斂性能(收斂速度和收斂精度)均比其它對比算法更優秀；但是在算法迭代后期，這7種算法均有“早熟”的情況，局部搜索能力沒有很好發揮。由表2的f2函數的對應avg可得，ARFWA的avg比其它對比算法更優。由表2的f5函數的avg可得，ARFWA的搜索能力比AFWA算法略差，但是比其它對比算法更優秀。

觀察f7函數尋優進化曲線圖(圖7)可知，當算法的迭代次數相等時，ARFWA呈現出的收斂性能(收斂速度和收斂精度)與其它對比算法相比實力相當，不分伯仲。由表2的f7的實驗結果avg可知，ARFWA尋找到的平均解avg不亞于其它對比算法。

觀察f8函數尋優進化曲線圖(圖8)可知，當算法的迭代次數相等時，ARFWA呈現出的收斂性能(收斂速度和收斂精度)稍差于AFWA，但是比其它對比算法更優秀。由表2的f8函數的結果avg可知，ARFWA、AFWA和EFWA求得的avg是一樣的，但是比其它對比算法更優。

觀察f10函數尋優進化曲線圖(圖10)可知，在尋優前期，當算法迭代次數相等時，ARFWA的收斂性能(收斂速度和收斂精度)稍差于AFWA，但是比其它對比算法突出；在算法尋優后期，7種算法均呈現出“早熟”的情況，局部搜索能力需要進一步提高。由表2的f10函數的avg可知，ARFWA求得的avg不亞于其它6種對比算法。

綜上可知，ARFWA總體的收斂性能優于其它6種對比算法。

3.4 各算法在測試函數的平均排名

為了更直觀看出各個算法的搜索能力，由表2的avg得到各算法在測試函數上的平均排名見表3，從表中可知，ARFWA在7種算法中排名第一，遠遠優于其它6種算法，即改進的煙花算法的整體搜索能力優于其它6種算法。

3.5 魯棒性分析

魯棒性的強弱可以通過標準偏差std的大小來判定。如果std越小，表示算法的魯棒性越強；反之，其魯棒性越弱。通過表2的實驗結果，對于f1、f3、f4、f5和f9測試函數，ARFWA、FWA和GPSO表現出的實力相當的魯棒性，且比其它4種對比算法更優秀；對于f2測試函數，ARFWA的魯棒性比FWA和GPSO兩種算法略弱，但是比其它4種對比算法更強；對于f6測試函數，ARFWA、SPSO和GPSO具有實力相當的魯棒性，且比其它4種對比算法更強；對于f7測試函數，ARFWA的魯棒性處于中等的實力，比SPSO、GPSO和AFWA這3種對比算法略弱，但比其它3種對比算法更強；在f8尋優過程中，ARFWA的魯棒性稍遜于AFWA，但是優于其它5種算法；在f10尋優過程中，ARFWA的魯棒性稍遜于SPSO、GPSO、EFWA，但優于其它3種算法。所以，綜上可得，在10個基準函數尋優過程中，ARFWA的魯棒性總體來說是比較好的。

3.6 尋優成功率分析

尋優成功一次是指在優化函數過程中，一次尋優的結果與理論最優值差值的絕對值不大于實驗設置的精度。由表4得，在迭代結束時，ARFWA尋優成功率均為100%的有8個基準函數；GPSO尋優成功率均為100%的有7個基準函數；FWA尋優成功率為100%的有6個基準函數；AFWA尋優成功率均為100%的有3個基準函數；SPSO、EFWA尋優成功率均為100%的只有2個基準函數；BA尋優成功率為100%的只有1個基準函數。所以，整體而言，在10個基準函數的尋優過程中，ARFWA的尋優成功率比較好。

3.7 討 論

通過實驗對比分析可以知道，改進的煙花算法ARFWA的整體性能比其它6種對比算法的更優秀體現在如下幾個方面：

(1)將粒子群算法的記憶機制引入改進的煙花算法中，借鑒了全局最優和個體最優的概念。本文引入sparkpBest來表示在尋優過程中每個煙花所產生的最優爆炸火花個體的集合以及gBest來表示全局最優煙花。當煙花的爆炸火花的數目大于或者等于平均爆炸火花的數目，說明該煙花向gBest學習，此時的煙花位于相對比較好的區域；反之，當煙花的爆炸火花數目小于平均爆炸火花數目時，說明煙花向sparkpBest學習，此時煙花處于相對比較差的區域；

(2)對全局最優gBest進行高斯擾動，以便增加種群的多樣性，避免出現“早熟”的現象；

(3)構造了新的爆炸半徑計算公式，標準的煙花算法對未被選擇的爆炸火花全部丟棄，沒有充分利用到被丟棄的爆炸火花的信息，而改進的煙花算法恰恰利用到這一點，將其充分利用，提高了煙花種群的信息利用率。

4 結束語

煙花算法是一種新穎的群智能算法，針對煙花算法后期收斂速度慢和求解精度不高的問題，充分利用了被舍棄的爆炸火花個體的信息，構造新的爆炸半徑計算公式，以便能夠自適應地調整步長；另外，在尋優的過程中，在原來高斯擾動的基礎上，對全局最優個體進行高斯擾動，以此平衡局部和全局搜索能力，避免煙花種群過快陷入局部最優，增強收斂速度和收斂精度。由仿真實驗可得：相對其它6種算法，整體而言，改進的煙花算法整體呈現出比較優秀的性能，表現在收斂性能方面(收斂速度更快、收斂精度更高)和魯棒性更強。

在接下來的研究工作中，將對ARFWA算法進行進一步的優化，并將其應用于實際中。