永磁同步電機常見故障建模與仿真研究

王小強，蘇建徽

(合肥工業大學 電氣與自動化工程學院，合肥 230009)

0 引 言

永磁同步電機(以下簡稱PMSM)運行可靠、控制靈活、效率高慣性低、輸出轉矩高，結構也簡單，在電動汽車、航天等領域應用廣泛。

近年來，出現了電機模擬器[1]的概念，專門用于模擬電機及其負載特性，它能夠模擬與電機相同的端口電氣特性，等效電機驅動器功率負載。其中，為測試電機驅動器在故障狀態下的性能指標，需要獲得能夠模擬出PMSM常見故障的電機模型。

PMSM的數學模型在三種坐標系下各有優缺點。自然(a,b,c)坐標系下的模型適用性廣泛；而同步旋轉(d,q)坐標系下的模型完成了解耦，從而較自然坐標系下的模型容易不少[2]；靜止(α，β)坐標系下，電機模型也實現了一定程度的解耦，且變換過程不需要坐標變換角，這在實際運用中也能節省一些DSP資源[1]。本文將分別在三種坐標系下進行了PMSM故障數學模型的推導及對比研究，以適應不同場合應用。

研究PMSM故障一般的模擬方法主要有兩種[3]：一種是用有限元分析法(FEA)建立故障模型，另一種則是在PMSM數學模型基礎上借助MATLAB/Simulink仿真平臺研究。文獻[4]對三相對稱短路穩態特性進行了數學理論推導，通過二維有限元法和實驗分析了永磁磁鏈、極對數、直流電感等電機本體參數對三相短路特性的交叉影響，但尚未從第二種方法來研究三相對稱短路故障。PMSM定子匝間短路故障也可以采用有限元分析法建立模型，但通過采用有限元建模對PMSM故障進行仿真，雖然精度高，但效率太低，計算速度慢，難以施加控制策略和工況[4]。為克服上述缺陷，采用集中參數的數學模型在MATLAB/Simulink上仿真是一種有效的方法。在對自然(a,b,c)坐標系下定子匝間短路故障建模時：文獻[5]對內置式PMSM進行了建模分析，由于表貼式PMSM電感較內置式PMSM簡單，其模型可以進一步簡化；文獻[4]研究表貼式PMSM，尋求將模型建得十分精確，在計算電機電感時引入泄露因子δbf而使得模型變得較為復雜，需要進一步改進。在對同步旋轉(d,q)坐標系下定子匝間短路故障建模時：文獻[6]研究了五相PMSM，三相PMSM需進一步推導；文獻[7]在對三相PMSM數學模型推導時未包含故障特征變量-短路電流if；文獻[7]在計算if時需同時獲得正常電機和故障電機的三相電壓，使得電機模塊翻倍而變得龐雜，需要進一步改進。文獻[8]對自然(a,b,c)坐標系下三相PMSM開路故障進行了數學建模，但未進行有限元或者Simulink建模仿真以驗證模型的正確性。在靜止(α,β)坐標系下對PMSM的匝間短路故障和開路故障的數學模型研究較少，還需要進行進一步的理論推導。

為彌補上述研究的不足，本文重新推導了在自然坐標系、旋轉坐標系和靜止坐標系下三種故障狀態下PMSM的數學模型，并在MATLAB/Simulink環境下進行了建模和對比仿真研究。

1 PMSM數學模型

三相PMSM由三相繞組及鐵心構成，電樞繞組常以Y型連接，在轉子結構上，PMSM用永磁體取代電勵磁，省去了勵磁線圈、滑環和電樞。

為便于分析，作以下假設：

(1) 忽略電機鐵心的飽和影響；

(2) 永磁材料的電導率為零；

(3) 電機的電流為對稱的三相正弦波電流；

(4) 不計電機的渦流和磁滯損耗。

在自然(a，b，c)坐標系下PMSM定子電壓方程：

(1)

電磁轉矩方程[9]：

(2)

式中:Uabc，Rabc，Iabc分別為三相繞組的相電壓、相電阻和相電流；ψabc為三相繞組的磁鏈；Te為電磁轉矩，p為極對數。在下面矩陣變量中，Ra=Rb=Rc=Rs為定子繞組電阻，ψf為永磁體磁鏈的值，L為電機自感，M為電機互感。

利用經典Park變換，可得在同步旋轉(d,q)坐標系下的數學模型，定子電壓方程：

(3)

電磁轉矩方程：

(4)

式中:ud,uq為定子電壓；R為定子繞組電阻；id,iq為定子電流；p表示微分算子；Ld,Lq為d,q軸等效電感；Te為電磁轉矩；p為極對數；ψf為永磁體磁鏈。

利用Clarke變換，可得PMSM靜止(α,β)坐標系下定子電壓方程如下：

[(Ld-Lq)(ωeid-piq)+ωeψf]·

(5)

電磁轉矩方程：

(6)

其中磁鏈方程：

式中:Uα，Uβ分別是PMSM在靜止坐標系下定子電壓；iα，iβ為定子電流；p表示微分算子；Rs為定子繞組電阻；Te為電磁轉矩；p為極對數；ωe為電角速度；ψα，ψβ為永磁體磁鏈。

另外，PMSM運動方程：

(7)

轉速、機械角速度、電角速度、角度公式：

(8)

ωe=pωm

(9)

(10)

式中：n為電機轉速；ωm為電機的機械角速度；TL為負載轉矩；ωe為電角速度；θ為轉子位置角；J為轉動慣量；B為阻尼系數。

2 PMSM三相短路故障下建模仿真

2.1 三相短路下數學模型

當PMSM莫明地發生三相對稱短路時，產生的暫態沖擊電流可能導致轉軸與繞組端部的嚴重機械應力損傷，還有永磁體的不可逆去磁。但三相短路也可主動作為保護動作來應用，比如運行過程中其它故障原因導致電機失控，可以主動采取三相對稱短路措施，隔離供電源保護電機，并且三相短路產生的制動轉矩也將迫使電機減速至穩定。圖1為PMSM三相短路示意圖。

圖1 PMSM三相短路示意圖

三相對稱短路穩態時，約束條件為定子三相電壓突降為零，故在自然(a,b,c)坐標系下定子電壓方程：

(11)

在同步旋轉(d,q)坐標系下定子電壓方程：

(12)

在靜止(α,β)坐標系下定子電壓方程：

[(Ld-Lq)(ωeid-piq)+ωeψf]·

(13)

2.2 仿真驗證

借助MATLAB/Simulink仿真平臺搭建PMSM在故障狀態下仿真模型，以驗證以上參數模型的有效性和正確性，將之代入基于閉環速度和電流控制的簡單三相PMSM矢量控制系統中，其中轉速環是由PI調節器構成，電流環由電流滯環控制器構成，如圖2所示。

圖2 PMSM矢量控制框圖

用于仿真的電機主要參數如下：運行速度1 000 r/min，母線直流電壓Udc=300 V，參考轉速n=1 000 r/ min，極對數p=3，定子電阻Rs=1.5Ω，相自感L=1.725 mH，相互感M=0.028 mH，轉動慣量J=0. 003 6 kg·m2，阻尼系數B=0.001 N·m·s。仿真條件設置：初始時刻負載轉矩TL=5 N·m，在t=0.05 s時設置三相對稱短路故障，獲得的仿真波形如圖3～圖5所示。

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

由圖3～圖5可以看出，PMSM正常和故障時三種坐標下的電機三相電流、轉矩及轉速都十分接近。另外從波形可知，在0.05 s發生故障時，出現的瞬態三相電流及轉矩都比穩態時大得多，此時出現的過電流是因為定子電壓突降為零，導致定子磁鏈空間矢量變化率也降為零，因為定子磁鏈不能突變，在系統中產生定子磁鏈直流分量，進一步引起電機的過電流，之后電流回歸穩態，轉速也因三相短路產生的制動轉矩在不斷下降至穩定。

3 PMSM匝間短路故障下建模仿真

PMSM定子繞組匝間短路故障常常是因為絕緣損壞導致，此后也許還會引起更嚴重的損壞。假設PMSM發生A相匝間短路故障，n為短路匝數，N為故障相總匝數，rf為短路電阻，Rf為短路匝內電阻，R為相電阻，則故障示意圖如圖6所示。

圖6 PMSM A相匝間短路示意圖

3.1 匝間短路故障在a,b,c坐標系下數學模型

與正常PMSM相比，發生匝間短路故障時電路中增加了故障環，假定用k表征故障的嚴重程度，通過分析，可得定子電壓方程：

(14)

其中各變量的含義分別如下：

Rb=(1-k)Rs

Rf=k(Rs+rf)

ψabcf=LsfIabcf+ψfFabcf(θ)

3.2 匝間短路故障在d,q坐標系下數學模型

不考慮電機磁場飽和，當PMSM發生A相匝間短路故障時，PMSM在匝間短路故障情況下的電壓方程式(1)可表示[10]：

(15)

當永磁同步電機A相發生故障時：

自然(a,b,c)坐標系變換到靜止(α,β)坐標系的坐標變換為Clarke 變換；Park變換則是將靜止(α,β)坐標系轉化成同步旋轉坐標系的變換。可通過Clarke/Park變換實現電機定子電壓方程從自然(a,b,c)坐標系到旋轉(d,q)坐標下的坐標變換：

Xdq=T(θ)Xabc

其中變換矩陣T(θ)：

定子電壓方程(15)經過上述變換后：

(16)

(17)

短路電流部分[11]計算公式：

而由d,q坐標系變換到a,b,c坐標系變換有：

Ua=Udcosθ-Uqsinθ

故可得：

(18)

3.3 匝間短路故障在α,β坐標系下數學模型

可通過Clarke變換實現的電機從自然(a,b,c)坐標系到靜止(α,β)坐標下的坐標變換，與在同步旋轉坐標下變換相似，當PMSM發生A相匝間短路故障時，可將式(15)由a,b,c坐標系變換為α,β坐標系：

Xαβ=X(θ)Xabc

其變換矩陣X(θ)：

(19)

對于表貼式PMSM，Ld=Lq，定子電壓方程式(15)經過上述變換后：

(20)

(21)

短路電流部分等式：

而由反Clarke變換有：

Ua=Uα

故可得：

(22)

3.4 仿真驗證

在上述同一PMSM的參數下，仿真條件設置：匝間短路故障系數k=0.3，初始時刻負載轉矩TL=5 N·m，獲得仿真波形，如圖7～圖9所示。

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

從以上仿真結果可以觀察到：發生匝間短路故障時PMSM在三種坐標下的仿真波形很接近，不過通過PI調節器實現的電流閉環跟蹤控制，難以消除電流跟蹤誤差， 因此三種坐標下的波形并不能完全一致[1]；在匝間短路故障時，故障A相電流幅值較其它兩相更大[12]，這是由于繞組不對稱，導致A相電流比其它兩相電流有更為明顯增大的高次諧波成分；電磁轉矩和轉速也產生了諧波成分，出現了小幅度波動。

4 PMSM開路故障下建模仿真

開路故障也是一種常見的電機故障。焊接不良，繞組短路，接地故障等都可以導致電機繞組開路。電機A相發生開路故障示意圖如圖10所示。

圖10 PMSM A相開路故障示意圖

4.1 開路故障在a,b,c坐標系下數學模型

假設定子繞組A相發生開路故障，則A相電壓Ua=0[13]，三相電流不再對稱[8,14]，A相電流由于電流傳感器出現輕微偏差,導致ia=iΔ不為0，但十分接近0，通常認為ia=0，電流方程滿足如下表達式：

(23)

故障時可代入定子電壓方程：

(24)

式中:Ua，Ub與Uc分別為三相電壓；ia，ib與ic為三相電流；Ra=Rb=Rc=Rs為定子繞組電阻；ψf為永磁體磁鏈值。

4.2 開路故障在d,q坐標系下數學模型

假定定子繞組A相發生開路故障，則通常認為ia=0。根據從同步旋轉d,q坐標系到自然a,b,c坐標系的變換：

可得:

ia=0=idcosθ-iqsinθ

(25)

根據Clarke 變換：

得：

Uβ=Udsinθ+Uqcosθ

(26)

將d,q坐標系下的定子電壓方程式(3)代入式(26)，則有：

(27)

為了消除計算電流id，iq時出現在分母中的sinθ，cosθ引起的奇異點，引入兩個輔助變量ρ和ξ，并令：

(28)

(29)

由式(25)可得：ρ=ξ，再將式(28)、式(29)代入式(27)，此時Uβ可用ρ變量表示，求解輔助變量ρ得：

(30)

求出ρ后，根據式(28)可得定子電流id，iq有：

(31)

此后即可順利求出電機中角速度、轉矩、轉速等其它變量，建立PMSM開路故障的電機模型。

4.3 開路故障在α,β坐標系下數學模型

為不失一般性和利于計算求解，假定PMSM定子繞組C相發生開路故障，其實對于單相開路而言假定C相或A相發生開路故障等效，則C相電壓Uc=0，且此時通常認為ic=0。根據反Clarke變換：

可得：

化簡得：

(32)

根據Clarke變換：

PMSM靜止坐標系下的定子電壓方程式如下，對于表貼式PMSM而言,Ld=Lq，可進一步簡化：

[(Ld-Lq)(ωeid-piq)+ωeψf]·

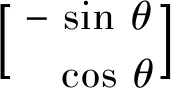
簡化后代入可得：

(33)

在得到iβ后，利用式(32)可得iα，后可順利求出電機中其它變量，獲得α,β坐標系下電機開路故障時電機模型。

4.4 仿真驗證

在上述同一PMSM的參數下，仿真條件設置：負載轉矩TL=5 N·m，t=0.05 s時設置PMSM單相開路故障，獲得仿真波形,如圖11～圖13所示。

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

(a) a,b,c坐標系

(b) d,q坐標系

(c) α，β坐標系

從以上仿真結果可以看出，當PMSM發生單相繞組開路故障時，三種坐標系下的波形很接近。與正常運行時的0～0.05 s時間段相比，故障時三相電流的幅值比正常時幅值要大，并且此時PMSM的電磁轉矩和轉速都產生了較大脈動。這是由于當某相電流突變為零時，這相磁動勢同樣是零，而定子電流合成的磁勢將會由圓形變成橢圓形，由此生成的橢圓形磁鏈將會生成接近電機轉速頻率的轉矩脈動。

5 結 語

本文圍繞PMSM三種常見故障，在三種坐標系下重新推導了數學參數模型，并采用MATLAB/Simulink建模仿真的方法來驗證。仿真結果表明，三種坐標系下的PMSM故障下的波形很接近；同時獲得了PMSM在三相對稱短路故障，匝間短路故障和開路故障的故障特征信息，可作為故障診斷、故障容錯和狀態監測的研究基礎。

本文在三種坐標系下都建立了PMSM的電機模型，能夠滿足在不同場合選擇合適的數學模型，也為PMSM模擬器系統提供了可供選擇的常見故障的電機模型，以此來測試電機驅動器在常見故障狀態下的性能指標。