三角恒等變換常見典型考題賞析
■尹志雄
作者單位:江蘇省揚州市寶應縣曹甸高級中學
題型1:三角函數公式的變形應用
三角函數公式變形應用需注意的兩個問題:①公式逆用時,一定要注意公式成立的條件和角之間的關系;②注意特殊角的應用,當式子中出現等數值時,一定要考慮引入特殊角。要熟記三角函數公式的變式,如sinαsinβ+cos(α+β)=cosαcosβ,cosαsinβ+sin(α-β)=sinαcosβ,tanα±tanβ=tan(α±β)·(1?tanαtanβ),cos2α=
例1 已知sin 76°cos46°-cos76°sin46°,則 sinα=( )。
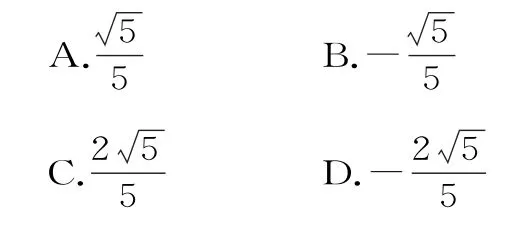
解:由tanα=sin76°cos 46°-cos 76°·,且α∈,可得由上容易得到應選A。
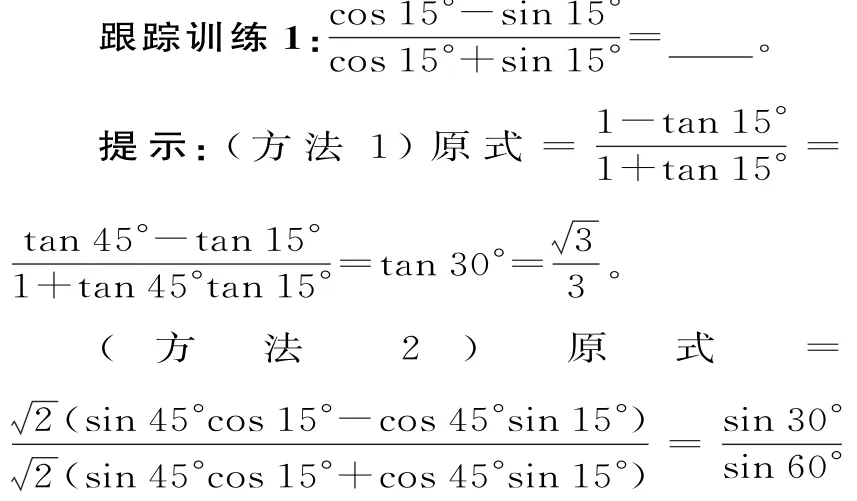
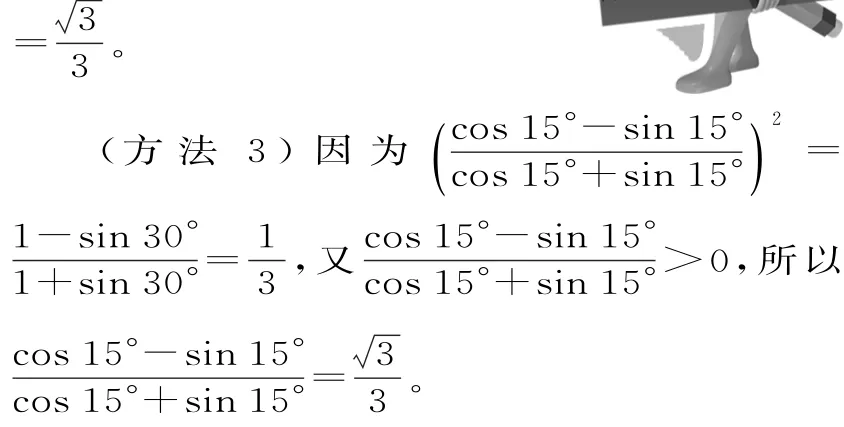
題型2:角的變換
熟練掌握常用的角變換技巧,如α=(α+β)-β=(α-β)+β,2α=(α+β)+(α-β),
例2 設α為銳角,若,則的值為( )。
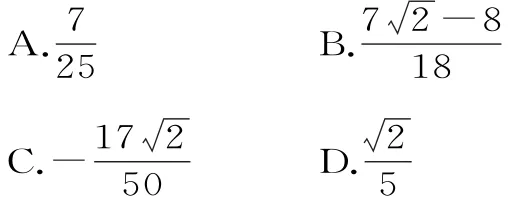
解:(方法1)因為α為銳角,所以。因為所以。應選B。
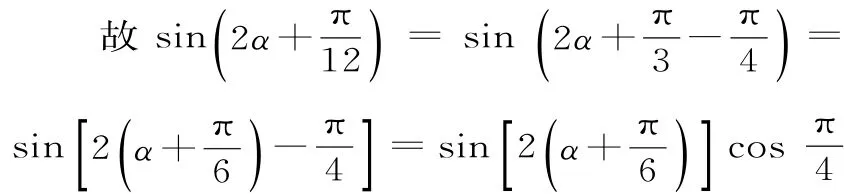
(方法2)因為α為銳角,所以又因為所以
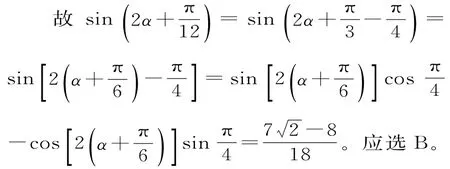
跟蹤訓練2:已知則的值是( )。
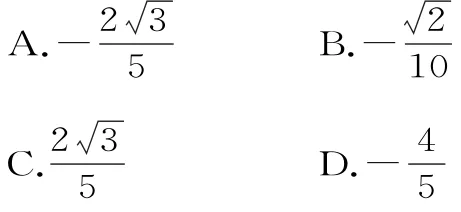
提示:由,可得
題型3:三角函數的圖像與性質問題
求解三角函數的奇偶性、周期性、單調性、最值等問題時,一般先要進行三角恒等變換,把三角函數式化為一個角的一種三角函數,再根據三角函數的奇偶性以及周期公式求解。解答這類問題的關鍵是熟練掌握三角函數圖像的應用。
例3 已知函數若將函數f(x)的圖像向左平移個單位長度,得到函數g(x)的圖像,則函數g(x)在區間]上的最大值和最小值之和為( )。
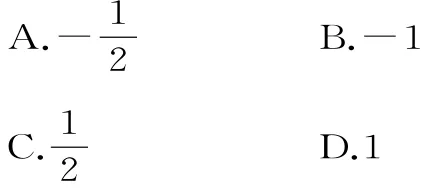
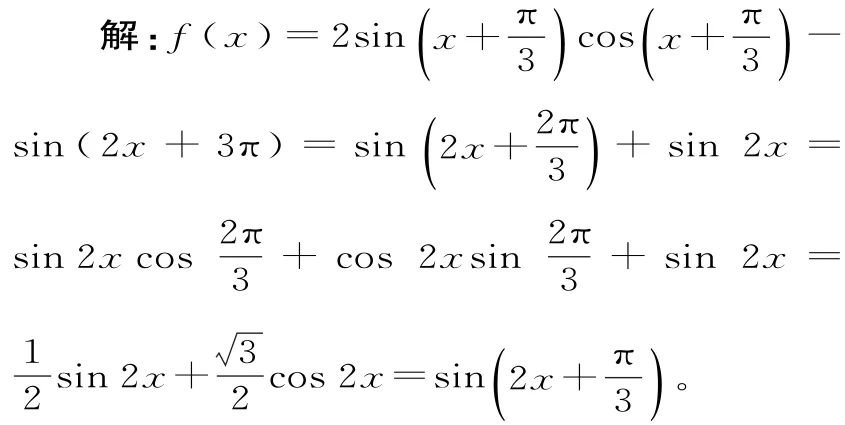
由題意可知函數g(x)=由,可得,可知當,即時,函數g(x)取得最小值,且g(x)min=-1;當,即x=0時,函數g(x)取得最大值,且故函數g(x)在區間上的最大值和最小值之和為應選A。
跟蹤訓練3:已知函數+θ)-cos(2x+θ)(-π<θ<0)的圖像關于點對稱,記f(x)在區間上的最大值為n,且f(x)在[mπ,nπ](m<n)上單調遞增,則實數m的最小值是____。
提示:因為的圖像關于點對稱,所以0。又因為-π<θ<0,所以,即θ=,這時當x∈即n=2。令當k=2時,即實數m的最小值是
題型4:非特殊角的求值問題
解答這類問題,要觀察所給角與特殊角間的關系,利用三角變換轉化為求特殊角的三角函數值的問題。此類問題也可通過代數變形(如正負項相消、分子分母相約)的方式來求值。

題型5:給值求值問題
給值求值問題的關鍵是找出已知式與待求式之間的聯系及函數的差異,一般可以適當變換已知式,求得另外某些函數式的值,以備應用,同時要注意變換待求式,便于將已知式求得的函數值代入,從而達到解題的目的。
例5 已知的值。
解:因為,且2sin2α-sinα·cosα-3 cos2α=0,則(2sinα-3 cosα)(sinα+cosα)=0(sinα+cosα≠0),所以2sinα=3 cosα。又sin2α+cos2α=1,所以cosα=。故原式=
跟蹤訓練5:已知sin(α-β)cosα-cos(β,其中β是第三象限角,則
提示:依題意可將已知條件變形為,可得sinβ=
因為β是第三象限角,所以cosβ=
題型6:三角函數的求角問題
這類問題的一般解題思路是:已知正切函數值,選正切函數,已知正弦或余弦函數值,選正弦或余弦函數。若角的范圍是,選正弦或余弦函數皆可;若角的范圍是(0,π),選余弦函數較好;若角的范圍為,選正弦函數較好。例6 已知A,B均為鈍角,且,則A+B=____。解:因為,解得又因為A為鈍角,所以cosA=由,且B為鈍角,可得cosB=
故cos(A+B)=cosAcosB-sinA·。又A,B均為鈍角,則A,B∈,所以A+B∈(π,2 π),由此可得A+
跟蹤訓練6:已知α,β∈(0,π),且tan(α,則2α-β的值為____。
提示:由tanα=tan[(α-β)+β]=,可得由,可得0<2α<。由,可得,所以-π<2α-β<0。因為tan(2α-β)=,故
題型7:三角函數與平面向量的交匯
平面向量與三角函數在“角”之間存在著密切的聯系。如果在平面向量與三角函數的交匯處設計命題,其形式多樣,解法靈活,且極富思維性和挑戰性。對于這類問題,根據所給三角式的結構及向量間的相互關系進行處理,可使解題過程得到簡化,從而提高解題的效率。
例7 已知向量a=(cos 2α,sinα),b=
解:由a=(cos 2α,sinα),b=(1,2sinα,且a·,可得cos 2α,即cos 2α+2sin2α-也即cos 2α+1-cos 2α-sinα=,所以可得
跟蹤訓練7:已知向量a=(cosθ,sinθ),向量則|2a-b|的最大值與最小值的和為____。
提示:由題意可得a·b=cosθ-sinθ,則∈[0,4],故|2a-b|的最大值與最小值的和為4。
題型8:三角函數中的新定義問題
近年來的高考試題相繼推出了以能力立意為目標,以增大思維容量為特色,具有相當濃度和明確導向的創新題型。這類創新題型大多以新定義問題的形式出現,值得同學們重視。新定義問題主要是指即時定義新概念、新公式、新定理、新法則、新運算,然后根據此新定義去解決問題,有時還需要用類比的方法去理解新定義,這樣有助于對新定義的透徹理解。
例8 已知下凸函數f(x)在定義域內滿足不等式若函數y=tanx在上是下凸函數,那么在銳角△A B C中,求tanA+tanB+tanC的最小值。
解:因為y=tanx在上是下凸函數,所以(tanA+tanB+tanC)≥,即tanA+,當且僅當tanA=tanB=tanC,即時等號成立,所以tanA+tanB+tanC的最小值為
跟蹤訓練8:已知函數y=f(x)(x∈R),對函數y=g(x)(x∈I),定義g(x)關于f(x)的“對稱函數”為y=h(x)(x∈I),y=h(x)滿足:對任意x∈I,兩個點(x,h(x)),(x,g(x))關于點(x,f(x))對稱。若h(x)=-asinx是g(x)關于f(x)=的“對稱函數”,且g(x)在上是減函數,則實數a的取值范圍是____。
提示:根據對稱函數的概念,可知h(x)+g(x)=2f(x),即g(x)=2f(x)-h(x)+1。令則函數+1,其對稱軸方程為,且圖像的開口向下。由于函數g(x)在上 遞 減 ,t=sinx在上遞增,根據復合函數的單調性可,即a≤2,故實數a的取值范圍為(-∞,2]。
題型9:三角函數中的恒成立問題
三角函數中的恒成立問題通常含有參數,解答這類問題,一定要注意三角函數自身的有界性,結合自變量的取值范圍,才能正確求解。
例9 已知不等式對于x∈恒成立,則實數m的取值范圍是____
解:因為所以原不等式等價于m≤在上恒成立。因為所以,由此可得m≤
,即實數
跟蹤訓練9:已知函數f(x)=,若對任意的實數α∈,都存在唯一的實數β∈[0,m],使f(α)+f(β)=0恒成立,則實數m的最大值是____。
提示:已知函數,若對任意的實數,則要使f(α)+f(β)=0 恒 成立,需滿 足f(β)∈,即,所以0≤,可得故實數m的最大值是

