變風載下風電齒輪箱內部激勵規律研究及動態特性優化

湯 亮，何仁杰，龔發云，李飛揚，劉冠軍，楊 敏

（1.湖北工業大學機械工程學院，湖北武漢430070；2.湖北省制造業創新方法與應用工程技術研究中心，湖北武漢430070）

隨著能源緊缺問題日益嚴峻以及風電技術高速發展，提高轉換效率、降低故障率和改善振動與噪聲已成為風電技術研究領域的重點。風電齒輪箱作為風電機組的核心部件，其傳動性能決定了整個風電機組的運行質量。因受到變風載引起的外部激勵及齒輪嚙合形成的內部激勵的影響，風電齒輪箱傳動系統產生巨大的振動與噪聲，加速了齒輪箱各零部件的疲勞損壞，造成一定的經濟損失。因此，對風電齒輪箱進行振動與噪聲的優化已成為一項重要研究。

為實現風電齒輪箱振動與噪聲優化，國內外許多學者已開展了相關研究，如：Guan等［1］基于所建立的齒輪傳動有限元模型，模擬了傳動系統的誤差激勵，并測得系統在此激勵下的振動響應；Zhao等［2］建立了由兩級行星輪系與一級斜齒輪副結構組成的風電齒輪箱的振動模型，并分析了在齒輪傳動誤差及嚙合剛度的影響下，風電齒輪箱動態特性的變化情況；Carbonelli等［3］從齒輪嚙合剛度和傳動誤差兩方面探究了齒輪箱輻射噪聲的形成原因，并基于齒輪修形技術優化了齒輪箱的內部激勵，改善和減小了其動態響應及噪聲；Switonski等［4］優化了齒輪宏觀參數，通過集中參數動力優化模型得到傳動齒輪的最小振動幅值；劉華朝等［5］通過齒輪齒向及齒廓修形的方式改善了其內部激勵，并分析了風電齒輪箱傳動系統輸出端響應加速度及噪聲的變化情況；方源等［6］通過實驗測試法研究了減速器的動態性能，為改善其嘯叫噪聲，基于多目標優化遺傳算法，確定了齒輪最佳修形值，并運用邊界元法分析了減速器輻射噪聲的變化情況；張霖霖等［7］根據所建立的齒輪傳動純扭轉動力學模型，研究了齒輪模數、齒數、螺旋角等宏觀參數對齒輪動態特性的影響規律，并通過Kato 公式預估了齒輪的輻射噪聲；陳思雨等［8］以齒輪副振動幅度作為衡量齒輪修形優劣的指標，在較大轉速范圍內研究了齒輪修形對齒輪傳動動態特性的影響。

從以上文獻分析可知，針對風電齒輪箱振動與噪聲優化問題，現有手段主要是通過齒輪修形來改善齒輪嚙合的內部激勵，從而實現齒輪箱傳動系統的減振降噪。但是，上述研究均在單一工況下確定齒輪修形量，而載荷、轉速等工況參數改變后，該修形量未必適用，且運用齒輪宏觀參數優化法來改善風電齒輪箱振動與噪聲的研究還較少。對此，筆者在建立風電齒輪箱動力學模型的基礎上，對多工況下風電齒輪箱傳動系統進行動力學仿真分析，應用遺傳算法尋求齒輪的最優修形量，使它在一定工況范圍內有較好的適用性；通過對基本齒條刀具的優化，以修改齒頂厚度、齒頂高度及齒根高度的宏觀參數優化法來增大齒輪重合度，并結合最優齒輪修形量來提升風電齒輪箱的動力學特性，以改善其振動及噪聲。

1 風電齒輪箱動力學模型構建及風載工況模擬

1.1 風電齒輪箱傳動系統

以某型號兆瓦級風電齒輪箱為研究對象，其傳動系統由兩級行星輪系及三級斜齒輪副組成，通過Romax Designer軟件建立風電齒輪箱傳動系統三維模型，如圖1所示。外部轉矩經一級行星輪系的行星架輸入、太陽輪輸出后，傳遞至二級行星輪系，二級太陽輪將轉矩傳遞至三級斜齒輪副輸入軸，最終由輸出軸輸出，以達到增速的效果。風電齒輪箱傳動系統各級齒輪副的基本參數如表1所示。

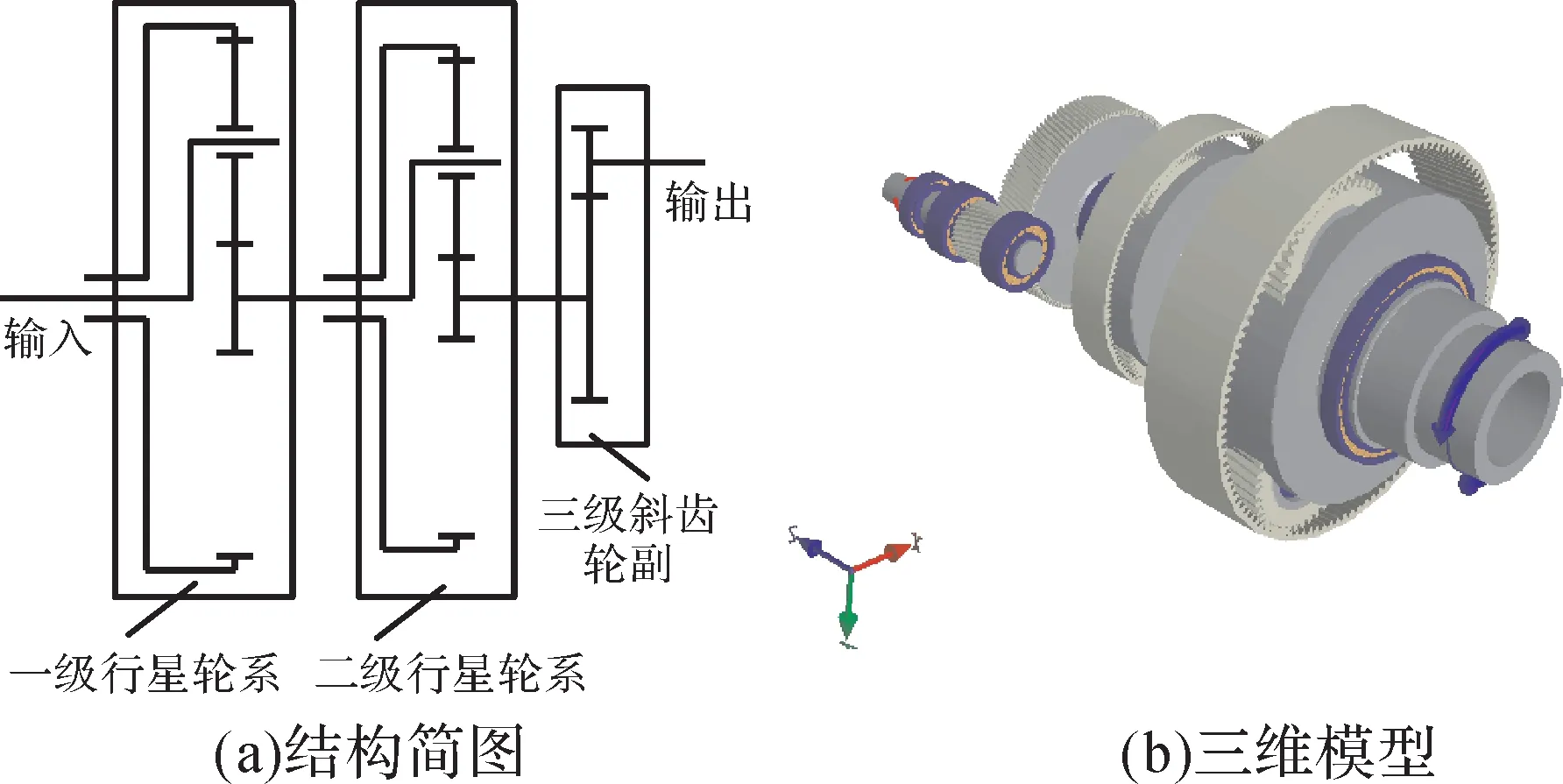
圖1 風電齒輪箱傳動系統結構簡圖及三維模型Fig.1 Structure diagram and three-dimensional model of wind turbine gearbox transmission system

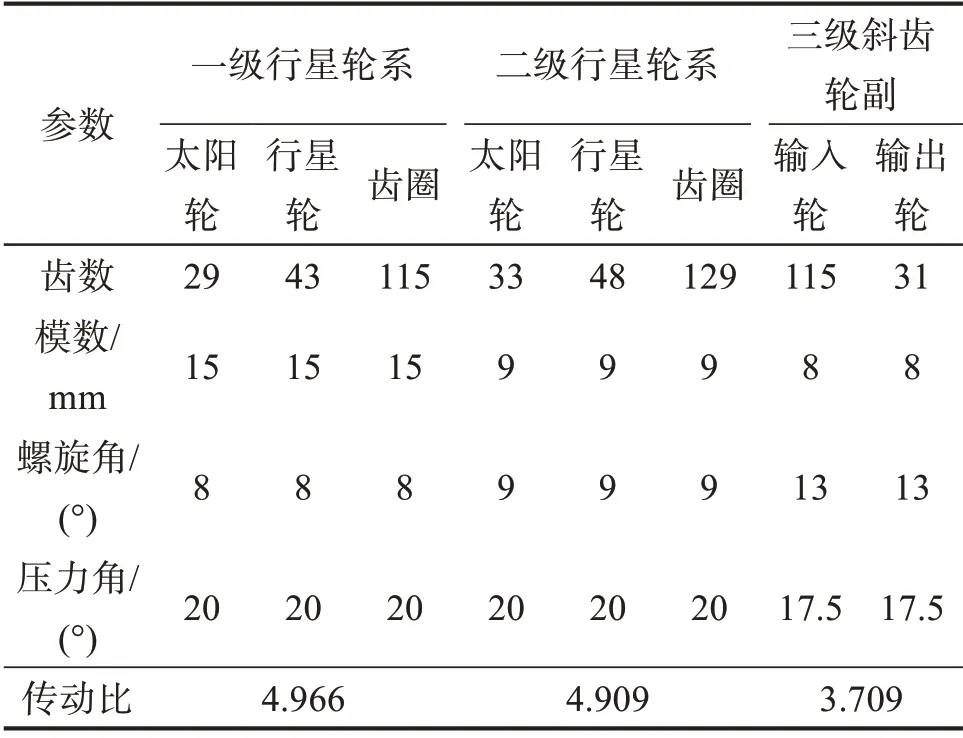
表1 風電齒輪箱傳動系統各級齒輪副的基本參數Table 1 Basic parameters of gear pairs in wind turbine gearbox transmission system

1.2 風電齒輪箱剛柔耦合動力學模型

考慮到箱體、行星架等部件的結構柔性，建立箱體及行星架等部件的有限元模型后，采用節點連接方式將各部件有限元模型與傳動系統三維模型耦合起來，并在箱體扭力臂處施加約束，以模擬機架對箱體的支撐作用。風電齒輪箱剛柔耦合動力學模型如圖2所示。

圖2 風電齒輪箱剛柔耦合動力學模型Fig.2 Rigid-flexible coupled dynamics model of wind turbine gearbox

圖3 為風電齒輪箱傳動系統動力學模型，圖中Ksi、Kpi、Kri、Kci、Kgη和Csi、Cpi、Cri、Cci、Cgη分別表示太陽輪、行星輪、齒圈、行星架、三級齒輪的耦合支撐剛度和阻尼，Kpiri、Cpiri分別表示行星輪-齒圈的嚙合剛度和嚙合阻尼，其中i=1，2，η=3，4。

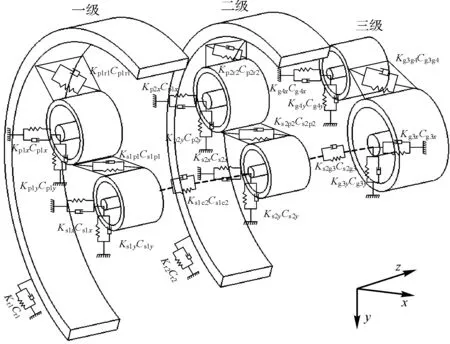
圖3 風電齒輪箱傳動系統動力學模型Fig.3 Dynamics model of wind turbine gearbox transmission system

在風電齒輪箱傳動系統各支撐部位建立耦合節點，將軸承、齒圈等部件的支撐剛度及阻尼與箱體有限元模型相耦合，確立耦合支撐剛度和阻尼后，計算各齒輪激勵下風電齒輪箱的動態響應。風電齒輪箱剛柔耦合動力學方程為：

式中：Mt(Mb)為傳動系統（箱體）質量矩陣；Ct(Cb)為廣義傳動系統（箱體）阻尼矩陣；Ctb(Cbt)為廣義傳動系統（箱體）耦合阻尼矩陣；Kt(Kb)為廣義傳動系統（箱體）剛度矩陣；Ktb(Kbt)為廣義傳動系統（箱體）耦合剛度矩陣；u¨t、u˙t、ut（u¨b、u˙b、ub）分別為傳動系統（箱體）的加速度、速度、位移向量；F(t)為系統內部動態激勵。

1.3 風電齒輪箱外部變風載工況

依據風電機組某一運行周期內的實測風載數據及空氣動力學公式［9］，計算風電齒輪箱傳動系統的輸入轉矩。為便于分析變風載下兆瓦級風電齒輪箱的動態特性，對載荷持續總時間進行歸一化處理，并將輸入轉矩曲線近似離散成10 種不同的轉矩工況（L01，L02，…，L10），如圖4所示。

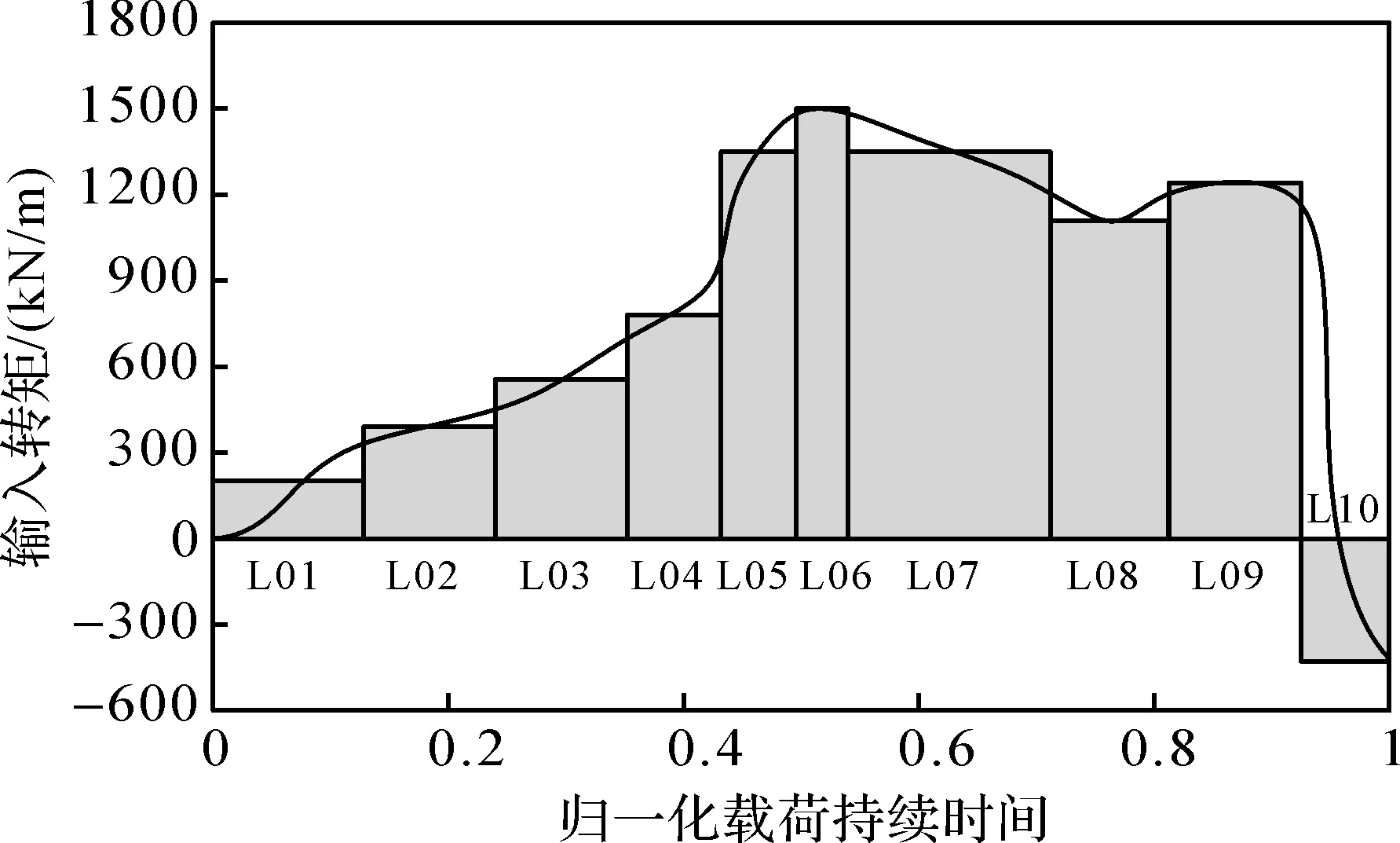
圖4 某一運行周期內風電齒輪箱傳動系統輸入轉矩Fig.4 Input torque of wind turbine gearbox transmission system in a certain operating cycle

2 變風載工況下風電齒輪箱傳動特性及響應分析

2.1 齒輪內部激勵

在齒輪傳動系統中，齒輪傳動誤差與嚙合剛度激勵是系統內部激勵的重要組成部分，亦是衡量系統振動與噪聲的關鍵指標［10-11］。

圖5（a）為10種工況下各級齒輪的傳動誤差值，可以看出，隨著工況的轉變，一級齒圈的傳動誤差曲線出現了較大起伏。L06工況下一級齒圈的傳動誤差如圖5（b）所示，其傳動誤差值（沿嚙合線位移的上下差值）達到最大值，為15.92 μm。一級太陽輪和二級齒圈的傳動誤差曲線的起伏趨勢次之，三級輸出輪及二級太陽輪的傳動誤差曲線較為平穩，幾乎未受到工況轉變的影響。由此可見，部分齒輪的傳動誤差受工況轉變的影響較大。

圖6所示為L06工況下三級斜齒輪的嚙合剛度，對于斜齒輪，綜合嚙合剛度的波動量即代表齒輪嚙合剛度激勵。

圖7為各級齒輪嚙合剛度激勵隨工況的變化曲線。行星架等部件的受載變形使各齒輪產生了偏心誤差，進而改變了齒輪總接觸線長度的變化范圍，造成嚙合剛度激勵發生變化［12］。由圖可以看出：一級、二級太陽輪的嚙合剛度激勵在前9個工況下均未變化，但在L10工況下均發生突變；其它齒輪的嚙合剛度激勵在不同工況下有較大變化。

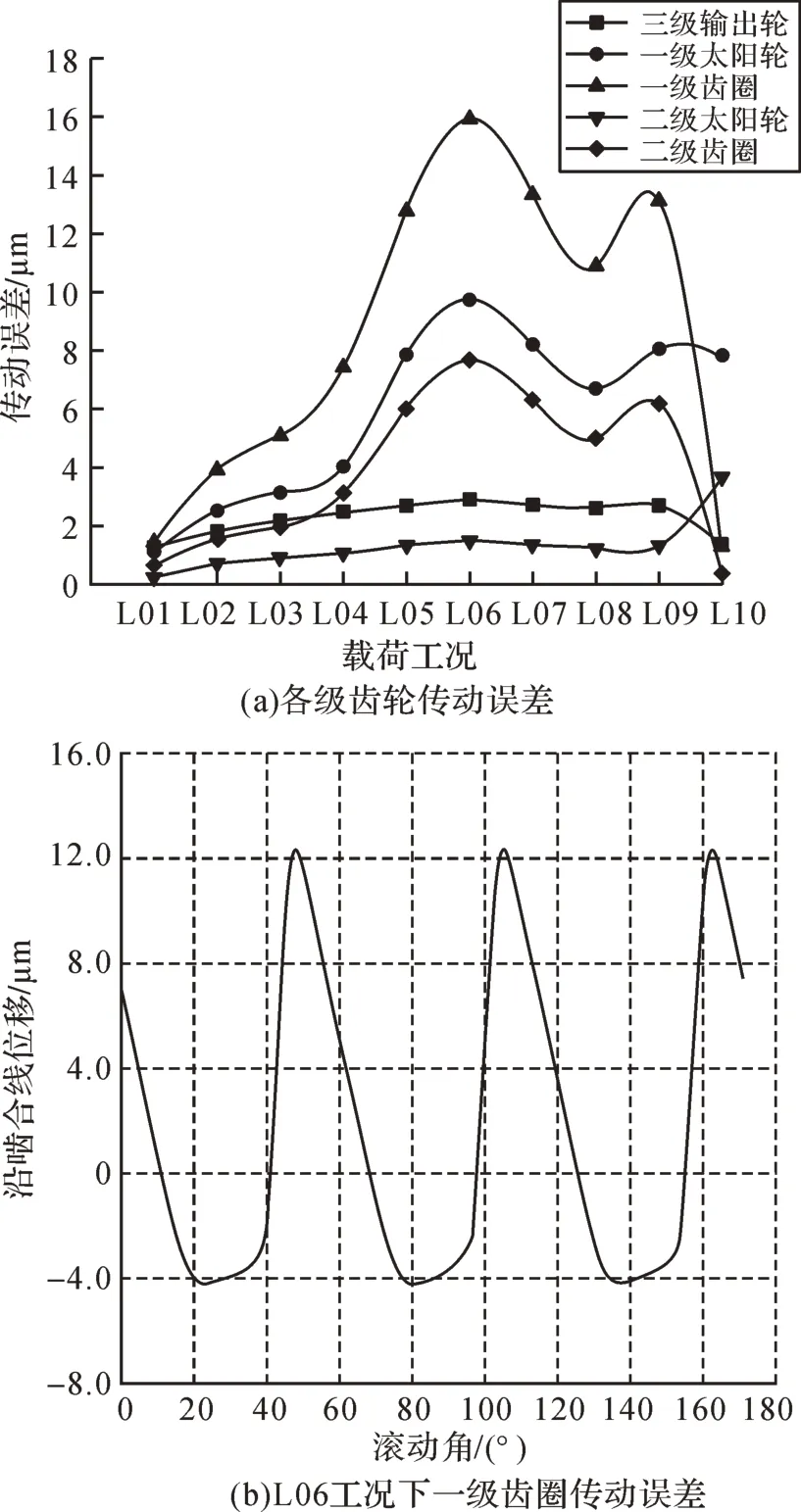
圖5 變風載工況下各級齒輪的傳動誤差Fig.5 Transmission error of gears under varying wind load condition

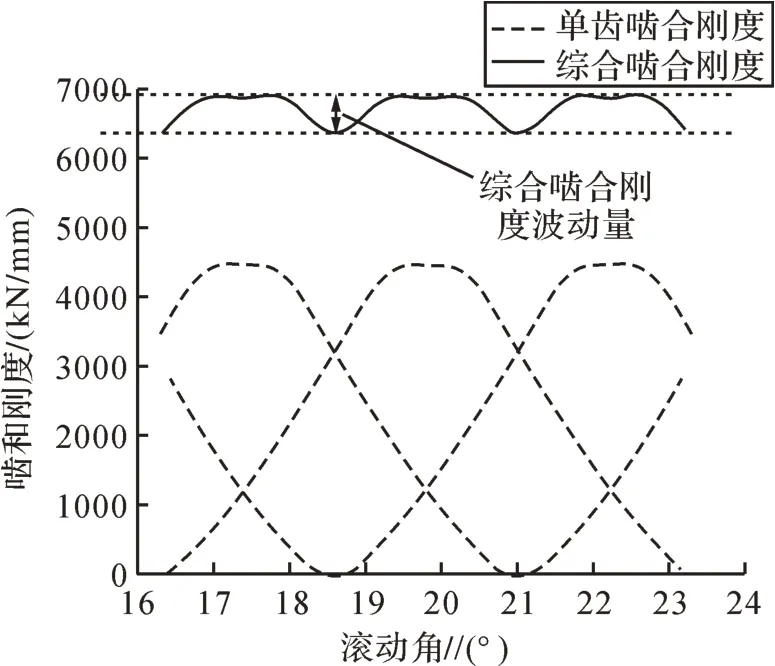
圖6 L06工況下三級斜齒輪嚙合剛度Fig.6 Meshing stiffness of third stage helical gear under L06 working condition

2.2 風電齒輪箱振動加速度分析

在齒輪內部激勵的影響下，風電齒輪箱三級下風向軸承座的振動能量最大［5］。因此，對齒輪箱三級輸入輸出軸軸承座進行振動加速度分析。如圖8所示，布置測點以檢測軸承座特定位置的振動加速度，其中：測點1用于輸出軸軸承座的加速度檢測，測點2用于輸入軸軸承座的加速度檢測。

圖7 變風載工況下各級齒輪的嚙合剛度激勵Fig.7 Meshing stiffness excitation of gears under varying wind load condition

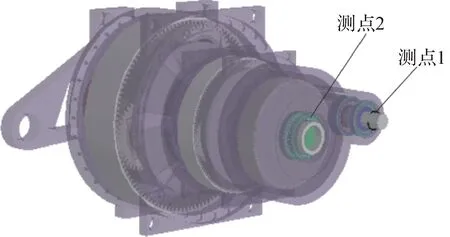
圖8 風電齒輪箱上測點布置Fig.8 Arrangement of measuring points on wind turbine gearbox

圖9為三級輸入輸出軸軸承座振動加速度隨工況的變化曲線。由圖可知，輸出軸軸承座的振動加速度明顯大于輸入軸軸承座，且在L05工況下兩軸承座的振動加速度均達到最大，分別為6.72 和3.91 m/s2。

圖9 風電齒輪箱三級輸入輸出軸軸承座振動加速度Fig.9 Vibration acceleration at third stage input and output shaft bearing seat of wind turbine gearbox

3 風電齒輪箱各級齒輪副優化

3.1 各級齒輪副宏觀優化

齒輪傳動的動態特性受其重合度的影響較大：重合度越高，齒輪傳動振動越小，且嚙合越平穩，噪聲越小［13-14］。以齒輪重合度為優化目標，以齒頂高度、齒根高度和齒頂厚度為設計變量，以齒頂間隙、根切間隙及齒條刀尖圓角半徑為約束條件，對風電齒輪箱各級齒輪副的宏觀參數進行優化。因優化過程中齒輪重合度的增大將導致齒頂厚度減小，從而顯著減小齒輪的彎曲強度，依據相關標準，為滿足齒輪彎曲強度要求，規定齒頂厚度/模數＞0.3［15］。

依據齒輪重合度公式［16］對風電齒輪箱各級齒輪副的重合度進行計算，其中式（2）用于計算行星輪系外嚙合齒輪的端面重合度，式（3）用于計算行星輪系內嚙合齒輪的端面重合度，式（4）用于計算三級斜齒輪副的端面重合度，式（5）用于換算齒輪齒頂壓力角與全齒高。

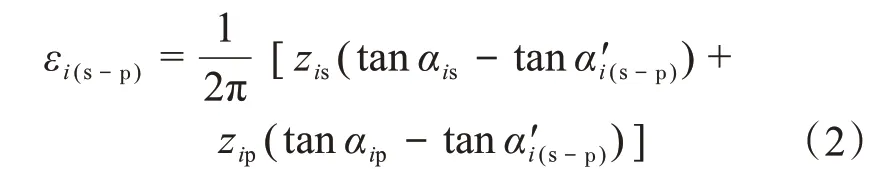
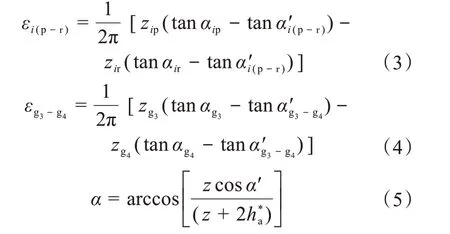
式中：εi(s-p)，εi(p-r)，εg3-g4分別為第i級（i=1，2）行星輪系的太陽輪-行星輪、行星輪-齒圈及三級斜齒輪副的端面重合度；zis，zip，zir，zg3，zg4分別為第i級行星輪系太陽輪、行星輪、齒圈及三級輸入輸出輪的齒數；αis，αip，αir，αg3，αg4分別為第i級行星輪系太陽輪、行星輪、齒圈及三級輸入輸出輪的齒頂圓壓力角；α'i(s-p)，α'i(p-r)，α'g3-g4分別為第i級行星輪系太陽輪-行星輪、行星輪-齒圈及三級斜齒輪副的嚙合角；α包括αis，αip，αir，αg3，αg4，α′包括α'i(s-p)，α'i(p-r)，α'g3-g4，z包括zis，zip，zir，zg3；為齒頂高系數。

通過增大齒輪副端面重合度，可增大齒輪副總重合度。優化前后風電齒輪箱各級齒輪副的宏觀參數和重合度如表2所示。

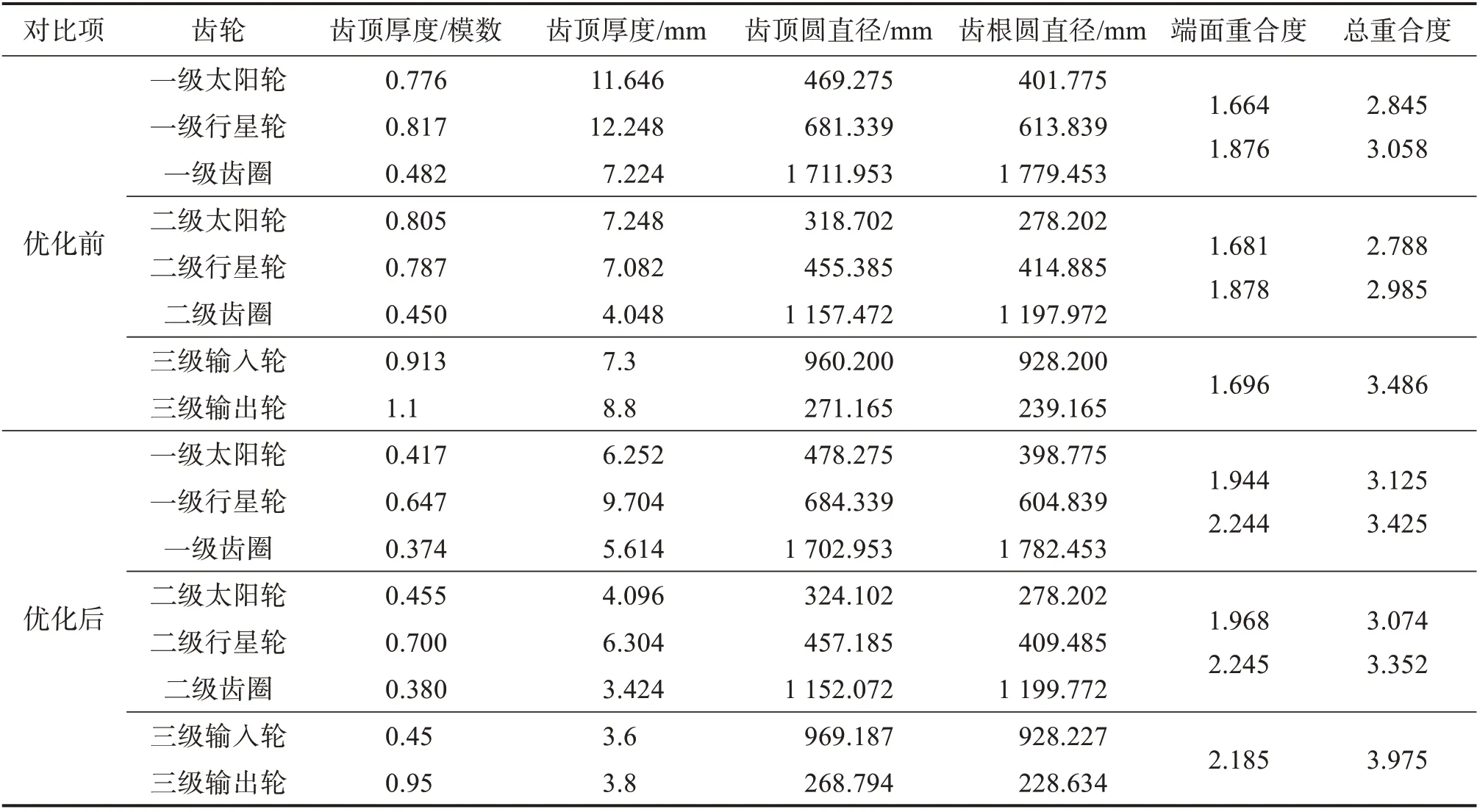
表2 優化前后各級齒輪副的宏觀參數和重合度Table 2 Macro-parameters and contact ratio of gear pairs before and after optimization

由表2可知，風電齒輪箱各級齒輪副的宏觀參數優化后，各級齒輪副的端面重合度及總重合度都得到了有效的提升。盡管優化造成齒頂厚度有一定削減，但仍滿足齒頂厚度/模數＞0.3的規定，在一定程度上保證了齒輪的彎曲強度。

3.2 各級齒輪副微觀優化

齒輪宏觀參數優化后，風電齒輪箱的傳動特性已得到一定程度的改善。但由時變風載引起的各部件的變形會導致風電齒輪箱各齒輪副仍有較大內部激勵及偏載。

齒輪修形是減小齒輪內部激勵及改善齒輪振動與噪聲的有效方法。由上文分析可知，齒輪傳動誤差及嚙合剛度受工況轉變的影響較大，若僅針對單一工況確立修形量，則在其它工況下，該修形量未必適用。因此，需尋得一組在多工況下均能達到理想效果的最優修形量。

遺傳算法是一種全局優化搜索算法，具有強魯棒性，可以解決復雜工況下齒輪修形量理論計算值存在偏差的問題，十分適用于齒輪修形設計研究［17］。

鑒于此，運用遺傳算法對變風載工況下各級齒輪修形量進行尋優計算，以各級齒輪齒廓鼓形量Cb、齒廓斜度βb、齒向鼓形量Ca及齒向斜度βa為優化變量（如圖10 所示，圖中h、b分別表示全齒高度及齒寬），以各級齒輪在所有工況下的內部激勵和σΣ最小為優化目標。在額定工況下運用齒輪修形經驗公式確立各級齒輪優化變量的取值范圍［18］。考慮到各工況運轉周期不同，在計算齒輪內部激勵和時應考慮各工況運轉周期占載荷持續總時間的權重，計算公式為：

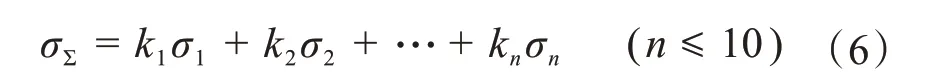
式中：kn為第n個工況的運轉周期占載荷持續總時間的比值，σn為以某修形量（種群個體）修形優化后，齒輪在第n個工況下的內部激勵。

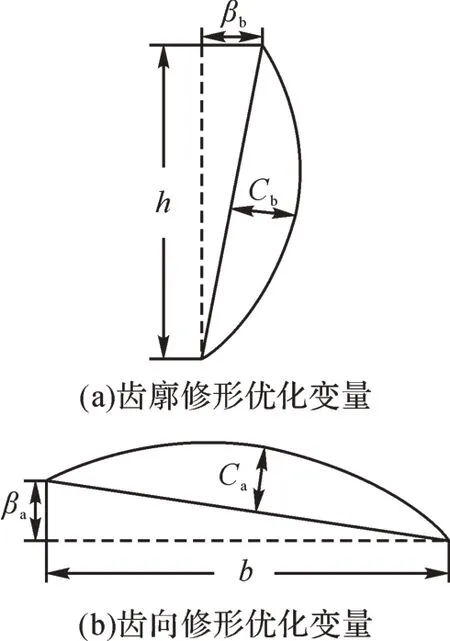
圖10 齒輪修形優化變量Fig.10 Gear modification optimization variables

設置遺傳算法種群數為100，變異系數為0.3，交叉系數為0.2，適應比為0.1，迭代次數為20，對變風載工況下各級齒輪修形量進行尋優計算，具體尋優流程如圖11所示。

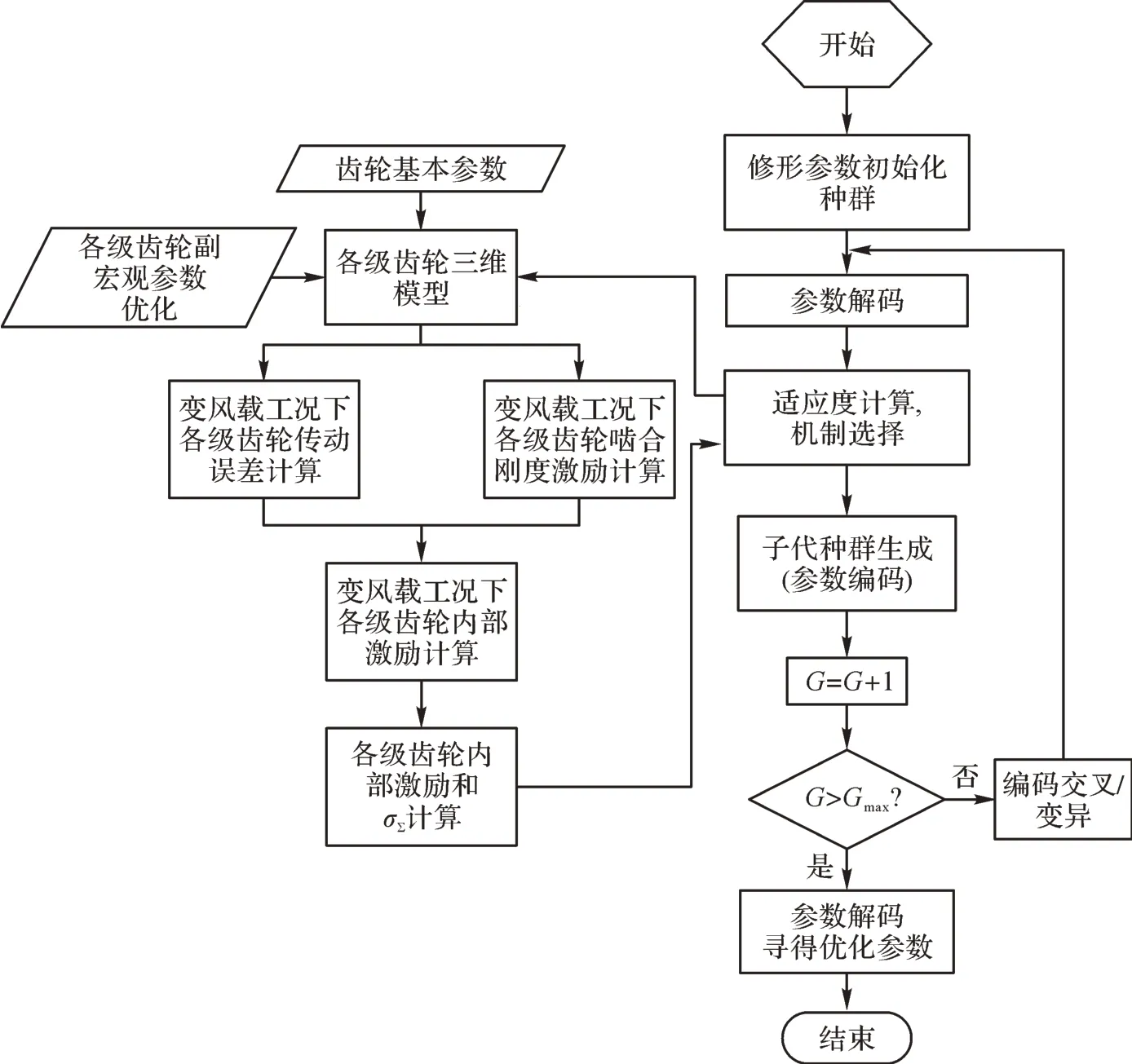
圖11 基于遺傳算法的齒輪修形量尋優流程Fig.11 Optimizing process of gear modification amount based on genetic algorithm

以三級輸出斜齒輪的齒向鼓形量尋優為例，通過圖12所示的單一修形量下的優化點陣圖可知，三級輸出斜齒輪的內部激勵和σ∑的最小值趨近于60。的各級齒輪的最優修形量代入Romax齒輪微觀修形模塊中，形成各級齒輪最優修形量云圖，如圖13 所示。由于風電齒輪箱運行時齒輪僅單向轉動，故只對一側齒面進行修形。

表4 風電齒輪箱各級齒輪的最優修形量Table 4 Optimum modification amount of gears in wind turbine gearbox 單位：μm

按上述流程對各級齒輪修形量尋優，得到風電齒輪箱各級齒輪的最優修形量，如表4所示。將所得

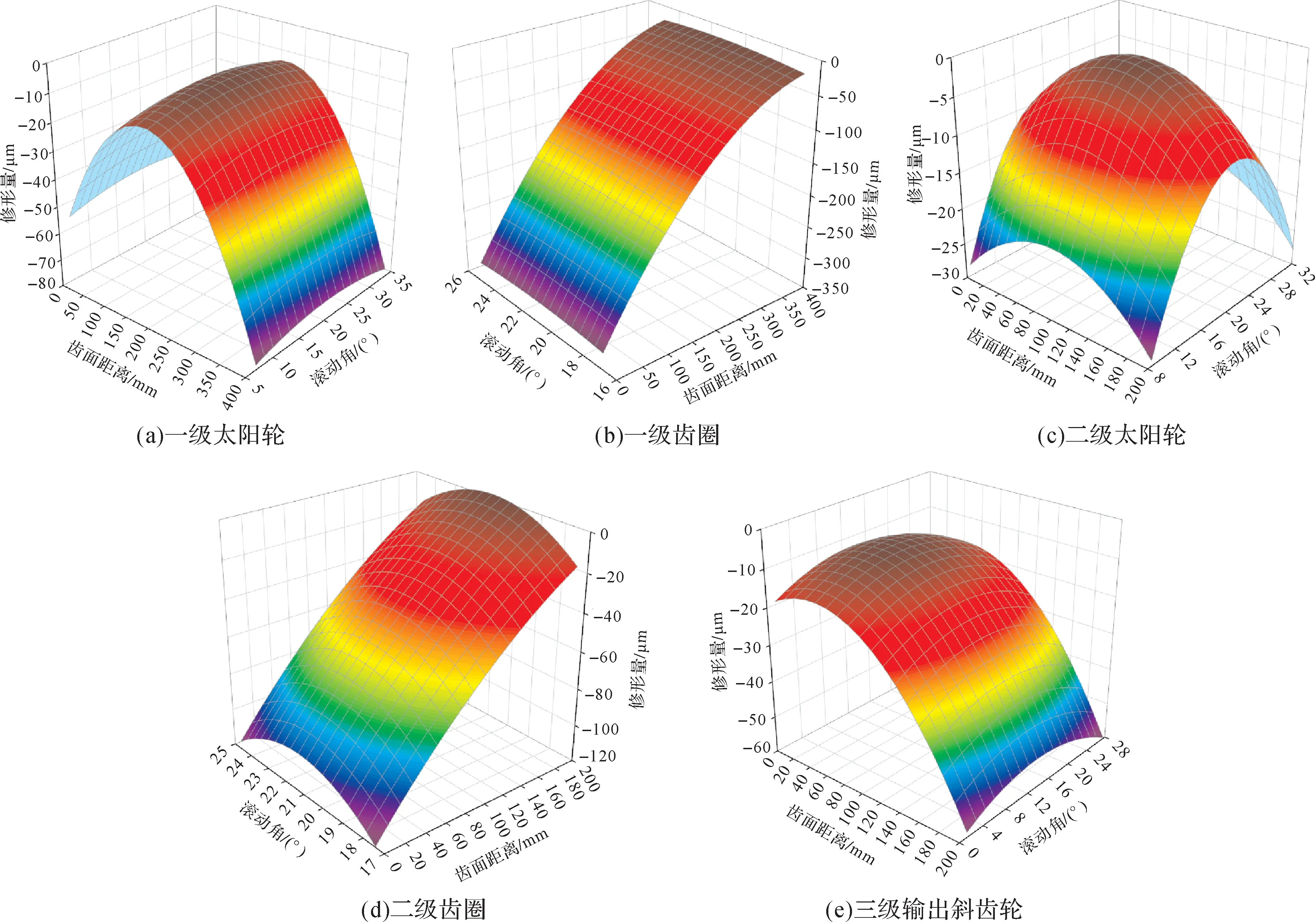
圖13 風電齒輪箱各級齒輪最優修形量云圖Fig.13 Nephogram of optimum modification amount of gears in wind turbine gearbox

4 變風載工況下優化后風電齒輪箱動態響應分析

4.1 優化后各級齒輪的傳動誤差

對優化后的風電齒輪箱各級齒輪進行傳動誤差分析，并與優化前的傳動誤差進行比較，結果如圖14所示。

由圖14可以看出：各級齒輪的傳動誤差顯著減小；對比優化前，優化后各級齒輪的傳動誤差隨工況轉變的起伏明顯平緩；在L06工況下，一級齒圈的傳動誤差由15.92 μm下降到了2.52 μm，改善了84.2%；但在某些工況下，該優化方法還存在不足，比如在L01、L02、L03工況下，一級齒圈的傳動誤差較優化前反而增大。不過從總體看，能取得多工況下的優化效果。

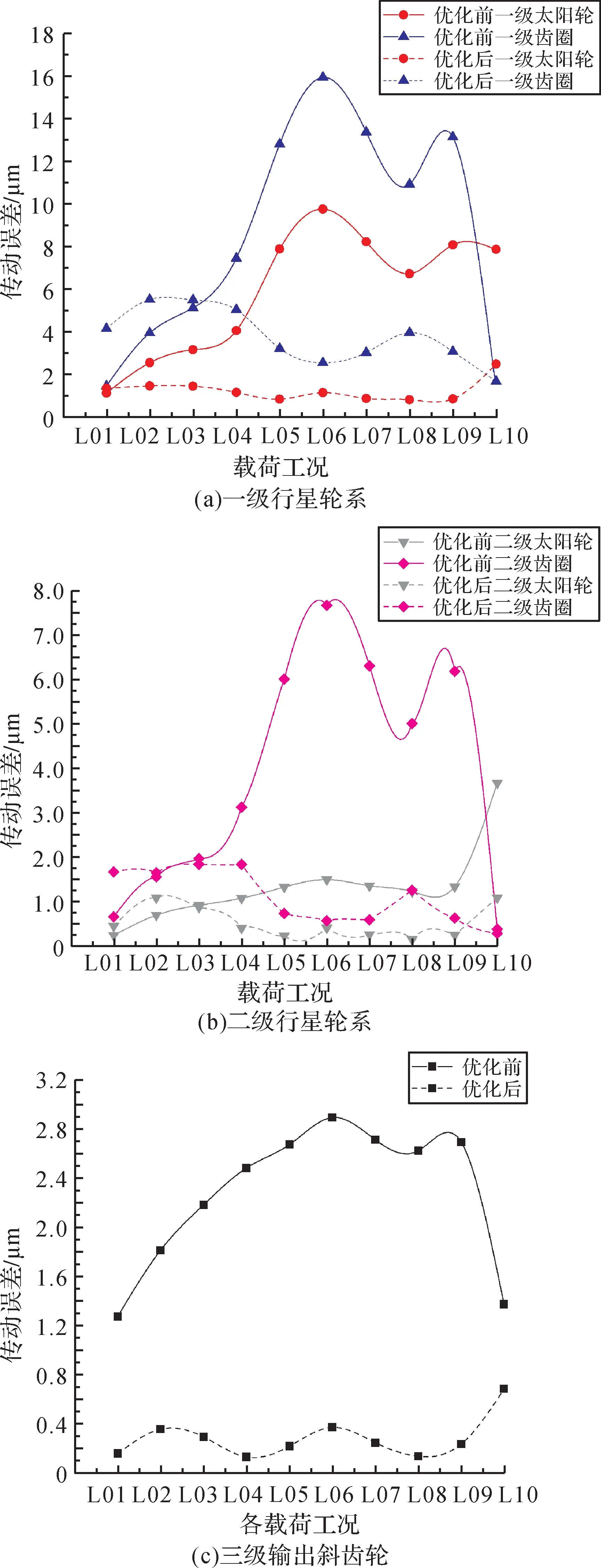
圖14 優化前后各級齒輪傳動誤差對比Fig.14 Comparison of transmission errors of gears before and after optimization

4.2 優化后各級齒輪的嚙合剛度激勵

圖15為優化前后風電齒輪箱各級齒輪嚙合剛度激勵的對比。

由圖15可知：通過宏觀參數優化和齒輪修形后，各工況下所有齒輪的嚙合剛度激勵均得到了有效改善；相對于傳動誤差的改善，各級齒輪嚙合剛度激勵的改善并未呈現不足。

圖15 優化前后各級齒輪嚙合剛度激勵對比Fig.15 Comparison of meshing stiffness excitation of gears before and after optimization

4.3 優化后三級輸入輸出軸軸承座振動加速度及噪聲

對優化后風電齒輪箱的三級輸入輸出軸軸承座進行振動加速度分析，并根據振動加速度級公式（7）計算三級輸入輸出軸軸承座的結構噪聲，結果如圖16所示。

圖16 優化前后三級輸入輸出軸軸承座振動加速度及結構噪聲對比Fig.16 Comparison of vibration acceleration and structural noise of third stage input and output shaft bearing seat before and after optimization

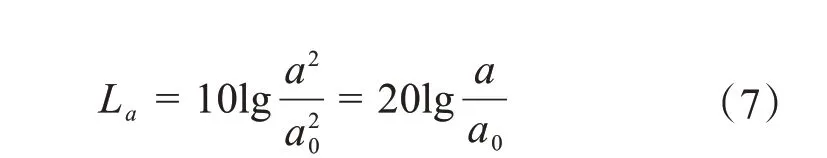
式中：La為結構噪聲，dB；a為軸承座加速度有效值，m/s2；a0為基準加速度，a0=1.00×10-6m/s2。

由圖16可以看出，優化后，各工況下三級輸入輸出軸軸承座的振動加速度及結構噪聲明顯減小，且相比于輸入軸軸承座，輸出軸軸承座振動加速度及結構噪聲的改善效果更為顯著。以輸出軸軸承座為例，優化前后各工況下其振動加速度及結構噪聲分別如表5 和表6 所示。由表可知，L02 工況下輸出軸軸承座振動加速度和結構噪聲的改善效果最優，振動加速度減小了17.2%，結構噪聲降低了1.7 dB。

5 結 論

1）以某型號兆瓦級風電齒輪箱為研究對象，考慮到箱體及行星架等部件的結構柔性，將各部件有限元模型與傳動系統三維模型以節點連接方式耦合起來，建立風電齒輪箱剛柔耦合動力學模型，并通過空氣動力學公式模擬了風電齒輪箱傳動系統的輸入轉矩。

2）分析了變風載工況下風電齒輪箱齒輪內部激勵變化規律，得出齒輪傳動誤差及嚙合剛度激勵受工況轉變的影響較大；分析了齒輪內部激勵下風電齒輪箱三級輸入輸出軸軸承座的振動加速度。

3）以齒輪修形量在多工況下有效為前提，以各級齒輪內部動態激勵和最小為優化目標，基于遺傳算法尋得適用于多工況的最優修形量，并與齒輪宏觀參數優化方式相結合，改善變風載工況下風電齒輪箱的動態特性。

4）對比變風載工況下優化前后風電齒輪箱的動態特性，結果表明：該風電齒輪箱的振動加速度及結構噪聲在各工況下均有明顯改善，振動加速度最大減小了17.2%，噪聲最大減小了1.7 dB。

表5 優化前后輸出軸軸承座振動加速度對比Table 5 Comparison of vibration acceleration at output shaft bearing seat before and after optimization

表6 優化前后輸出軸軸承座結構噪聲對比Table 6 Comparison of structural noise at output shaft bearing seat before and after optimization 單位：dB