一種基于疊加Logistic映射分布的FWA-PSO新算法

孫小川 劉太安 魏光村 王波 盧昱波

摘 要：為了解決傳統粒子群算法早熟收斂陷入局部最優、粒子中期震蕩及收斂結果不精確的問題，提出一種基于疊加Logistic映射分布的FWA-PSO算法對其進行改進。具體方法是：疊加Logistic映射用于對粒子位置的混沌初始化，在粒子數量一定的情況下，平衡最大遍歷路徑與最快收斂速度;引入FWA算法，同時根據迭代次數與粒子位置標準差，基于懲罰機制非線性調整爆炸半徑r、慣性權重w、個體學習因子c1和社會學習因子c2，融合高斯變異算子與循環單維度尋優策略，在維系粒子群多樣性的同時，也能避免粒子越過最優解。實驗結果表明：FWA-PSO算法針對單峰函數50次平均值均能達到最優解0，證明了算法的穩定性與可靠性;對于多峰函數，FWA-PSO算法也能求得最優解，證明該算法可跳出局部最優，得到全局最優解。

關鍵詞：粒子群算法;疊加Logistic映射;FWA算法;懲罰機制;循環單維度尋優

DOI：10. 11907/rjdk. 192155 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP312 文獻標識碼：A 文章編號：1672-7800（2020）002-0001-06

英標：A FWA-PSO New Algorithm Based on Superposition Logistic Map Distribution

英作：SUN Xiao-chuan1， LIU Tai-an1，2， WEI Guang-cun1，2， WANG Bo2， LU Yu-Bo2

英單：（1. College of Computer Science and Engineering， Shandong University of Science and Technology，Qingdao 266590，China;2. Department of Informaion Engineering，Shandong University of Science and Technology，Taian 271019，China）

Abstract： In order to solve the problem that the traditional particle swarm algorithm premature convergence is trapped in local optimum， the medium-term oscillator is inaccurate， and the convergence result is inaccurate， an improved algorithm is proposed， i.e.， FWA-PSO （Fireworks Algorithm - Particle Swarm Optimization） algorithm based on superimposed logistic map distribution. The specific method is as follows： superimposed Logistic map is used to initialize chaotic of particle position， balance the maximum traversal path and the fastest convergence speed when the number of particles is constant; FWA algorithm is introduced， and based on the number of iterations and the standard deviation of particle position. Based on punishment the mechanism nonlinearly adjusts the blast radius r， the inertia weight w， the individual learning factor c1 and the social learning factor c2， and combines the Gaussian mutation operator with the cyclic one-dimensional optimization strategy to maintain the particle group diversity while avoiding the particles crossing the optimal solution. The experimental results show that the FWA-PSO algorithm can achieve the optimal solution for the 30-time average of the unimodal function， which proves the stability and reliability of the algorithm. For the multi-peak function， the FWA-PSO algorithm can also find the optimal. The solution proves that the algorithm can jump out of the local optimum and get the global optimal solution.

Key Words： particle swarm optimization; superimposed logistic mapping; FWA algorithm; penalty mechanism; cyclic one-dimensional optimization

0 引言

PSO（Particle Swarm Optimization）算法由Kennedy&Eberhart[1]提出，是一種基于群體智能的全局隨機搜索算法，模擬了鳥群覓食的遷徙和群聚行為。與遺傳算法相比，PSO算法是單向信息流，只是把信息傳遞給其它粒子。群體遷徙的本質是尋找全局最優解并向其靠近，在迭代過程中，不斷更新每個粒子尋找到的最優解與全局最優解，并且PSO沒有“交叉”和“變異”操作[2]，收斂效率高、調整參數少，僅需調整慣性變量w、個體學習因子c1和社會因子c2的值，即能以較低的時間復雜度找到較為滿意的解[3]。因此，相比于其它優化算法，效率更高的PSO算法成為現代優化方法領域的研究熱點。

但PSO算法也存在不足之處，具體包括：在迭代過程中容易陷入局部最優，且跳不出局部陷阱;粒子收斂中后期會發生震蕩，收斂速度變慢;收斂結果不精確等。針對以上問題，國內外學者提出了多種解決策略，如Shi等[4-6]提出帶慣性變量w的速度更新公式，迭代時可維持上一代的趨勢，增強了粒子在空間中的全局搜索能力;Liang等[7]提出一種綜合學習粒子群優化算法（CLPSO），每個粒子速度更新時會參考其它粒子的全局最優解，通過綜合學習策略，準確更新速度和位置;Liu等[8]利用混沌遍歷思想提高局部搜索能力，使后期收斂結果更加精確;Pires等[9]將分數階微積分引入粒子速度更新公式，使用分數階階次控制算法收斂速度。此外，為避免種群陷入局部最優，Dong等[10-14]引入自適應變異機制，在迭代過程中基于高斯變異[15-17]自適應調整參數。雖然學者們提出了多種解決方案，但是算法本身仍然存在缺陷。為了彌補算法的不足，本文提出一種基于疊加Logistic映射分布的FWA-PSO（Fireworks Algorithm——Particle Swarm Optimization）算法。

該算法會使粒子位置基于疊加的Logistic映射混沌序列[18-20]初始化，遵循空心規則，在滿足粒子群最大遍歷路徑的同時，也平衡了與收斂速度的關系;重新設計慣性權重w、個體學習因子c1和社會因子c2的非線性迭代公式，該公式分為全局公式和局部公式，且有控制進化速度的參數n。n值越大，全局性或局部性越強;融入FWA算法[21-22]，利用算法的爆炸性與局部覆蓋性，結合高斯變異算子，為粒子賦予跳出局部最優的概率，并能找到局部最優解;同時針對高維多峰問題提出循環單維度尋優策略，利用基準函數測試后，可知該算法能顯著提高全局搜索性能和收斂精度。

1 基本PSO算法

PSO算法是為了求解連續變量優化問題而提出的，其特征是模擬鳥群智能。在PSO算法中，每個優化問題的潛在解都是一個粒子，在鳥群中是搜索空間中的一只鳥。所有粒子都有一個由被優化函數決定的適值（Fitness Value），以及一個決定其飛翔方向和距離的速度，然后粒子追隨當前最優粒子在解空間中進行搜索。粒子的速度和位置也在解空間中通過隨機初始化產生，然后通過迭代找到最優解。每次迭代中，粒子通過跟蹤兩個極值更新自己。兩個極值一個是粒子本身找到的最優解，稱為個體極值，另一個是整個種群當前找到的最優解，稱為全局極值。

假設在一個D維目標搜索空間中，由N個粒子組成一個群落，其中第i個粒子表示為一個D維向量。

第i個粒子的“飛行”速度也是一個D維向量，記為：

第i個粒子迄今為止搜索到的最優位置稱為個體極值，記為：

整個粒子群迄今為止搜索到的最優位置稱為全局極值，記為：

找到這兩個最優值時，粒子根據式（5）、式（6）更新自己的速度和位置。

其中，c1、c2為學習因子，也稱為加速常數，w為慣性因子，r1、r2為[0，1]范圍內的均勻隨機數。式（5）右邊由3部分組成，第一部分為反映粒子運動習慣的慣性權重部分，代表粒子有維持自己先前速度的趨勢;第二部分為反映粒子對自身歷史經驗記憶的個體學習認知部分，代表粒子有向自身歷史最佳位置逼近的趨勢;第三部分為反映粒子間協同合作與知識共享群體歷史經驗的社會學習認知部分，代表粒子有向群體或鄰域歷史最佳位置逼近的趨勢。

2 PSO算法缺陷分析與改進策略

2.1 粒子早熟收斂分析

標準PSO算法在多峰函數下，容易早熟收斂至局部最優，本質原因包括兩方面：①粒子位置及速度初始化不適合，導致后期遍歷路徑少，未搜索至全局范圍;②公式參數設計不恰當，導致粒子在進化過程中多樣性迅速消失，無法突破局部最優。針對這兩種原因，提出以下解決對策：粒子從疊加Logistic映射的混沌序列中選取，增加粒子遍歷路徑;改進參數調整公式，更合理且更有側重性地調整慣性權重和學習因子。

2.1.1 疊加Logistic映射的混沌粒子

粒子位置初始化一般為解空間的隨機值，假設某一函數的解空間為圓c=x2+y2，x，y=[-1，1]，全局最優解為pg=（0，0），粒子位置為解空間均勻分布的隨機值，在x軸上的粒子平均遍歷路徑如式（7）所示。

若要增加遍歷路徑，粒子應該在解空間初始化為臨邊分布，使[|xi|]取最大值。在標準PSO公式下分析粒子兩種分布的收斂速度，如圖1所示。

橫坐標x為迭代次數xi，縱坐標y為粒子位置以極值點為均值的標準差sd。圖1（a）粒子初始化為均勻分布，圖1（b）粒子初始化為臨邊分布，設置標準差值sd<0.1為迭代終止條件，測試50次取平均值。臨邊分布迭代次數/均勻分布迭代次數約為1.25，可知臨邊分布收斂速度較差。為平衡最大遍歷路徑與最快收斂速度，提出粒子空心分布規則。分布規律如式（8）所示。

[？（j）]代表第j區間的粒子密度，sj代表第j區間面積（一維長度，二維面積，依此類推），k代表粒子初始化由邊界至中心的等分區間個數。為了使粒子分布大致遵循公式（8），提出疊加Logistic映射分布。

Logistic映射也稱為Logistic迭代，其是一個時間離散的動力系統，函數如式（9）所示。

其中，zk∈[0，1]， ∈[0，∞）R。當μ=3.65，3.66，3.68，4.0時，在[0，1]區間迭代生成的混沌時間序列如圖2所示。

由圖2可知，選取區間[0.3，0.9]的粒子可以近似滿足式（8），粒子分布也近似屬于空心規則。通過一定映射關系，將圖2依據初始范圍[-100，100]轉化為二維粒子位置初始化映射序列分布圖，如圖3所示。

2.1.2 基于懲罰機制的自適應參數調整策略

對于公式（5），合理設置w、c1、c2也可以一定程度上突破局部最優。較大的w、c1有利于粒子進行全局搜索，較小的w、c1有利于粒子進行局部搜索。因此，很多學者對固定的w提出各種改進策略，比較經典的有線性遞減策略、隨機策略和非線性遞減策略。非線性遞減策略如式（10）所示。

為了在粒子中后期仍然保持較大的w，提升粒子搜索深度，故將w作了改進，公式如下：

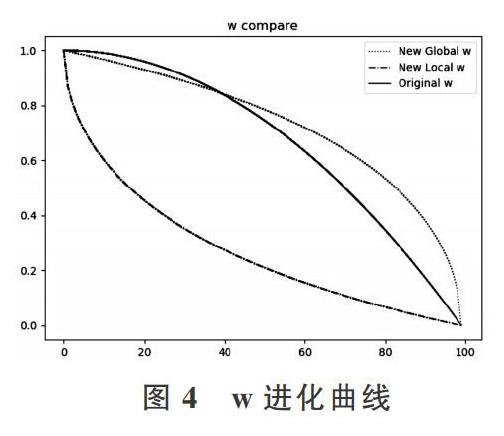
式（11）[wG]趨向于全局收斂，而式（12）[wL]則趨向于局部收斂。t為當前迭代次數，T為總迭代次數。n用來控制進化中的w值，n越大，作用越明顯。[wmax]和[wmin]用于控制w的最大與最小范圍。圖4展示了當迭代總次數為T時，3種w進化曲線。

在搜索初期，一般采用較大的c1和較小的c2，有利于粒子群體搜索整個空間，而在搜索后期，較小的c1和較大的c2則有利于群體收斂于全局最優。基于此，粒子的個體學習因子c1可以采用非線性遞減策略，而社會學習因子c2可以采用非線性遞增策略，如式（13）、（14）所示。

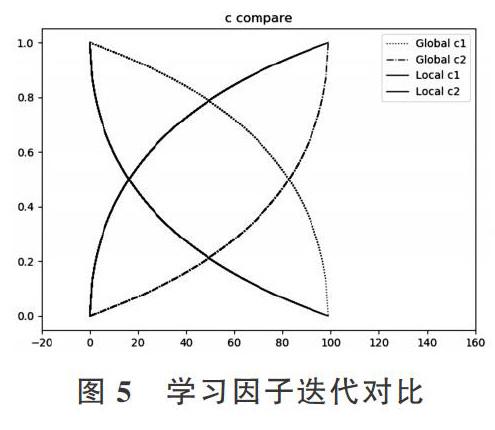
[c1G]、[c2G]學習因子偏向于全局搜索，而[c1L]、[c2L]學習因子偏向于局部搜索。[c1max]、[c1min]分別用控制個體學習因子的最大、最小范圍，[c2max]、[c2min]分別用于控制社會學習因子的最大、最小范圍。t為當前迭代次數，T為總迭代次數，n用來控制進化過程中學習因子c值大小。圖5展示了當T=100時，4種學習因子c的進化曲線。

在粒子進化過程中，不合適的參數設置也會導致粒子在全局最優值附近產生震蕩徘徊現象，大大降低了收斂速度。

如圖6所示，迭代次數在120～160之間時，位置標準差sd值在5.0上下震蕩，雖然粒子最終會收斂，但增加了額外運行開銷。為了避免出現這種情況，本文提出基于懲罰機制的自適應參數調整策略，當位置標準差sd>1，且最近5次迭代得到[sd]的標準差小于0.1時，w、c1和c2應等于[wL]、[c1L]、[c2L]，懲罰因子n增加1，達到快速收斂的效果，如式（15）所示。

[sd]代表最近5次位置標準差平均值，[sdj]是第j次位置標準差，P為最近5次[sd]值的標準差。

2.1.3 循環單維度尋優策略

粒子群在處理高維問題上有天然的弊端，這是因為在尋找全局最優解的同時，每一維度均會受到其它維度干擾，當維數增大時，擾動更為明顯。為了降低多維度對粒子群算法的干擾，本文提出循環單維度尋優策略。

對于一個D維向量的Gbest，從第一維開始，將1維元素g1設置為變量，2～D維元素固定為常數，衍生出n個子向量，然后對子向量進行迭代。如圖7所示，此時已將多維問題轉化為一維問題。同樣，下次以第2維為變量，一直持續到第n維。

每一次循環迭代，得到的結果Gbest總會比之前的最優適應度值更好，所以該循環算法的尋優軌跡是可取的，不會存在Gbest變差的情況。

2.2 FWA-PSO算法

傳統粒子群算法的全局最優解經過有限次迭代后收斂精度不高，而融入FWA群體智能算法后，可以提高收斂精度。FWA算法由Tan&Zhu在2010年正式提出，當時二人受到了煙花在夜空中爆炸產生火花并照亮周圍區域這一現象的啟發。利用FWA算法的局部覆蓋性，可以增強粒子的局部搜索能力，從而在算法運算后期更加精準地搜索最優解。

粒子在迭代搜索過程中，粒子位置會逐漸靠近，sd值會逐步遞減至0，設定限值為se。當sd

[ri]代表第i維的FWA爆炸半徑，爆炸區域為解空間的小比例空間。λ為控制閾值數量級因子，[ximax]、[ximin]為粒子第i維的最大、最小值。

加入高斯變異算子得到式（18），對于爆炸半徑r產生一個服從Gaussian分布的隨機擾動項，可以在粒子爆炸時增加半徑大小的不確定性，有利于粒子跳出局部最優，提高全局搜索能力。

經過變異后的半徑如式（19）所示。

3 疊加Logistic映射分布的FWA-PSO算法步驟及仿真實驗

3.1 算法步驟

Step1：確定粒子群規模N、初始化區間、速度上下限、最大迭代次數T、倍數η、閾值數量級因子λ等參數，并根據上文方法對粒子位置進行混沌似正態初始化。

Step2：更新粒子位置與速度。

Step3：計算粒子群局部最優值和全局最優值。

Step4：計算各粒子的適應度值，并根據迭代次數和中期震蕩條件動態自適應調整慣性權重w、個體學習因子c1與社會學習因子c2。

Step5：更新各粒子個體極值與全局極值。

Step6：若達到停止條件，輸出全局極值;若未達到停止條件，但達到爆炸觸發條件，經高斯變異調整爆炸半徑R，轉向Step1;若循環次數達到設定值，執行一次循環單維度尋優算法，返回Step2;若停止條件和爆炸觸發條件均未達到，返回Step2。

3.2 算法流程

算法流程如圖8所示。

3.3 仿真實驗

為了驗證本文提出FWA-PSO算法的收斂性能，將FWA-PSO算法與文獻[4]中帶慣性的粒子群算法PSO-ω、文獻[7]中的綜合學習粒子群優化算法CLPSO以及文獻[8]中的混沌粒子群算法CPSO進行比較。實驗采用6個常用標準測試函數，如表1所示。這些函數中包括單峰函數和非線性高維多模態函數，往往容易使算法陷入大量局部最優點，屬于優化領域中較難優化的函數。

Sphere、Matya是用來驗證算法收斂速度的單峰函數，Griewank至Rosenbrock是用來驗證算法跳出局部最優能力的多峰函數。慣性因子w取值區間為[0.5，0.8]，初值為0.8，個體學習因子c1及社會學習c2的取值區間為[1.5，2.5]，c1初值為2.5，c2初值為1.5。初始化粒子數為20，測試函數維度為30，基準函數評價次數FEs為200 000。算法所得結果均為50次運行結果的平均值。

表2中的gbset為算法在測試過程中得到的最優解，mean為50次運行結果平均值。通過表2中各算法實驗結果數據對比可知，本文提出的PWA-PSO算法在各測試函數上的運行結果都表現較好。

由表2可以看出，與帶慣性參數的PSO-w算法、綜合學習CLPSO算法及混沌CPSO算法相比，FWAPSO算法在30維的高維復雜基準函數測試中表現更為穩定，針對單峰函數Sphere和Matyas，50次平均值均能達到最優解0，證明了算法的穩定性與可靠性。對于多峰函數Griewank、Rastrigin、Ackley，FWA-PSO算法平均值也能求得最優解，說明該算法可跳出局部最優，全局搜索能力更好。Rosenbrock是比較困難的優化函數，因為其屬于高維多峰不可分函數，每一維優化均與相鄰維度存在隱性關聯，但在多次優化中，FWAPSO算法仍能求出最優解，多次平均值也遠小于其它幾種算法。因此，本文提出的FWAPASO算法具有更高的尋優精度與更強的尋優能力，更適用于解決其它算法難以解決的高維多峰函數優化問題。

4 結語

本文主要針對傳統PSO算法存在的缺陷，包括容易陷入局部最優、粒子中后期震蕩、收斂結果不精確幾類問題進行分析，并提出一種基于疊加Logistic映射分布的FWA-PSO算法對其進行改進。粒子位置初始化由疊加的Logistic映射混沌時間序列產生，遵循空心分布原則，在保持收斂速度的同時，增加了粒子遍歷路徑，有利于提高全局搜索能力，避免遺漏部分解空間的搜索;通過非線性調整慣性權重、個體學習因子與社會學習因子，將參數分為偏向全局搜索與偏向局部搜索兩種類型，根據不同情況選擇更合適的參數公式;循環單維度算法明顯提高了多維尋優效率，減少了迭代次數;融合FWA算法利用其局部覆蓋性及高斯變異多樣性，在不喪失全局搜索能力的同時，也能得到更為精確的局部最優值。仿真結果表明，本文提出算法相較其它算法具有更好的性能。后續工作將重點研究算法收斂性、時間復雜度及高維多峰函數各維度之間的隱性關系，以進一步提高算法性能。

參考文獻：

[1] KENNEDY J，EBERHART R.? Particle swarm optimization[C]. Perth：Proceedings of International Conference on Neural Networks，1995.

[2] MICHALEWICZ Z，JANIKOW C Z，KRAWCZYK J B. A modified genetic algorithm for optimal control problems[J].? Computers & Mathematics with Applications， 1992， 23（12）：83-94.

[3] REYES-SIERRA M， COELLO C C A. Multi-objective particle swarm optimizers： a survey of the state-of-the-art[J]. International Journal of Computational Intelligence Research，2006（3）：287-308.

[4] SHI Y H，EBERHART R C. A modified particle swarm optimizer[C].? IEEE World Congress on Computational Intelligence，1998：69-73.

[5] SHI Y H，EBERHART R C. Empirical study of particle swarm optimization[C]. Congress on Evolutionary Computation，2002.

[6] SHI Y，EBERHART R C. Fuzzy adaptive particle swarm optimization[C]. Proceedings of the 2001 Congress on Evolutionary Computation，2001：101-106.

[7] LIANG J J，QIN A K，SUGANTHAN P N，et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation， 2006， 10（3）：281-295.

[8] LIU B，WANG L，JIN Y H，et al. Improved particle swarm optimization combined with chaos[J]. Chaos， Solitons and Fractals， 2005， 25（5）：1261-1271.

[9] PIRES E J S，MACHADO J A T，OLIVEIRA P B D M，et al. Particle swarm optimization with fractional-order velocity[J]. Nonlinear Dynamics， 2010，61：295-301.

[10] PING-PING D. Improved particle swarm optimization with adaptive inertia weight[J]. Computer Simulation，2012（6）：874-880.

[11] ZHAN Z H，ZHANG J，LI Y，et al. Adaptive particle swarm optimization[J]. IEEE Transactions on Cybernetics，2010，39（6）：1362-1381.

[12] DAS S，GOSWAMI D，CHATTERJEE S，et al. Stability and chaos analysis of a novel swarm dynamics with applications to multi-agent systems[J]. Engineering Applications of Artificial Intelligence，2014， 30：189-198.

[13] GONG Y J. Genetic learning particle swarm optimization[J]. IEEE Transactions on Cybernetics， 2017， 46（10）：2277-2290.

[14] ANGELINE P J. Evolutionary optimization versus particle swarm optimization： Philosophy and performance differences[C]. International Conference on Evolutionary Programming Springer，1998：601-610.

[15] 姚凌波，戴月明，王艷. 反向自適應高斯變異的人工魚群算法[J]. 計算機工程與應用， 2018，54（1）：179-185.

[16] 杜艷艷，劉升. 帶有高斯變異的Lévy飛行改進蝙蝠算法[J]. 微電子學與計算機，2018， 35（3）：83-87.

[17] 黃海燕，彭虎，鄧長壽，等.? 均勻局部搜索和高斯變異的布谷鳥搜索算法[J]. 小型微型計算機系統， 2018，39（7）：77-84.

[18] JIANG M， SHEN Y， JIAN J， et al. Stability， bifurcation and a new chaos in the logistic differential equation with delay[J].? Physics Letters A， 2006， 350（3）：221-227.

[19] SHI Y， YU P. On chaos of the logistic maps[J]. Dynamics of Continuous Discrete & Impulsive Systems，2007，14（2）：175-195.

[20] 楊莘元，王光，谷學濤.? Logistic混沌序列性能分析及應用仿真[J]. 郵電設計技術，2003（12）：19-22.

[21] 譚營，鄭少秋. 煙花算法研究進展[J]. 智能系統學報，2014，9（5）：515-528.

[22] 包曉曉. 改進混沌煙花算法的多目標調度優化研究[J]. 計算機應用研究， 2016，33（9）：2601-2605.

（責任編輯：黃 健）