一種改進RANSAC算法的單應性矩陣估計方法

李嘉惠 張豐收 崔浩陽

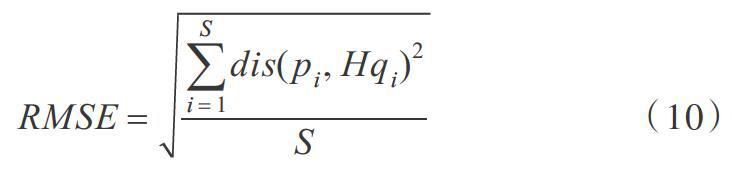
摘 要：在圖像拼接技術中，單應性矩陣是實現兩幅圖像正確拼接的關鍵因素。針對傳統RANSAC算法誤匹配點概率較高，需要設置固定的投影誤差閾值t導致迭代次數多、運行時間長、估計的單應性矩陣精度低等問題，提出一種改進的RANSAC算法以降低誤匹配率。利用特征點周圍灰度梯度相似性，剔除初始匹配中部分誤匹配點，以減少矩陣估計的迭代次數;通過快速舍棄錯誤的單應性矩陣以減少內點檢測時間，提高算法運行效率;通過BGD算法最小化損失函數以擬合精確的單應性矩陣。對比實驗結果表明，改進的RANSAC算法能夠有效剔除誤匹配點，減少內點檢測時間，提高單應性矩陣H的精度。

關鍵詞：圖像匹配;RANSAC算法;單應矩陣;BGD算法;誤匹配點

DOI：10. 11907/rjdk. 191439 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP317.4 文獻標識碼：A 文章編號：1672-7800（2020）002-0149-04

英標：A Homography Matrix Estimation Method Based on Improved RANSAC Algorithm

英作：LI Jia-Hui1，ZHANG Feng-shou1，CUI Hao-Yang 2

英單：（1.College of Mechanical and Electrical Engineering， Henan University of Science and Technology， Luoyang 471003， China;2.College of Mechanical and Electrical Engineering and Automation， Shanghai University， Shanghai 201900，China）

Abstract： In image stitching technology， the homography matrix is the key factor to achieve the correct stitching of two images. The traditional RANSAC algorithm has a high probability of mismatching points and needs to set a fixed projection error threshold t and it will lead to many iterations， long running time， and low accuracy of the estimated homography matrix. An improved RANSAC algorithm is proposed to reduce the mismatch rate. The similarity of gray gradient around feature points is used to eliminate some mismatched points in initial matching， so as to reduce the iteration times of matrix estimation. By quickly discarding the wrong homography matrix， the detection time of the inner point is reduced， and the operating efficiency of the algorithm is improved. The loss function is minimized by the BGD algorithm to fit the exact homography matrix. According to the results of the comparative experiment， the improved RANSAC algorithm can effectively eliminate the mismatch points， reduce the inside point detection time， and improve the accuracy of the homography matrix H.

Key Words： image matching; RANSAC algorithm; homography matrix; BGD algorithm; mismatch point

0 引言

圖像拼接技術是指將一組具有相互重疊部分的圖像進行空間匹配對準，經重采樣融合成一幅包含各圖像序列信息的寬視角場景、可理解性更好的新圖像[1-2]。圖像配準是指根據兩幅圖像重疊區的一致性求解圖像之間的投影變換，即平面單應性矩陣，廣泛應用于三維重建、目標跟蹤和機器人視覺等領域[3-4]。目前圖像配準方法研究最多、應用最為廣泛的是基于特征點的圖像配準方法。在特征點匹配過程中，不可避免地會產生誤匹配[3-6]，目前有很多消除誤匹配的方法，如霍夫聚類法、最小中位法以及隨機抽樣一致性算法（Random Sample Consensus，RANSAC）等等。其中，RANSAC由Fischler & Bolles在1981年提出，廣泛應用于圖像拼接領域。文獻[7]中，在提取圖像的 SIFT 特征點后，根據閾值法對特征點進行初始匹配，然后采用改進的RANSAC 算法對初始匹配對篩選，再計算圖像間單應性矩陣，最后使用加權平均的融合方法實現圖像的無縫拼接，可靠性較高但效率較低;文獻[8]提出了一種改進的全景圖自動拼接算法，利用 RANSAC 算法去除誤匹配，但是估計的單應性矩陣精度低，拼接效果一般;文獻[9]中，在改進的RANSAC算法中改用8對特征點匹配點對，確保對應8個特征點皆為內點，從而大大降低迭代次數，提高運算效率;文獻[10]重復采用兩次 RANSAC 算法引導匹配，降低了單應性矩陣估計效率;文獻[11]首先進行初步篩選，然后利用相似三角形求出基準單應性矩陣，設定閾值，剔除不滿足閾值的匹配點對，最后得到精確匹配點。一般當匹配對超過一半外點時，RANSAC算法就能估計出正確的單應性矩陣。但是在內點概率[ω]非常小的情況下，迭代次數將非常高，導致運算效率降低。

目前基于RANSAC算法的單應性矩陣估計均存在精度低、算法運行時間長等問題。因此，本文提出一種改進RANSAC算法的單應性矩陣估計方法，能夠有效剔除誤匹配點，減少運行時間，顯著提高單應性矩陣精度。

1 RANSAC算法基本原理

RANSAC算法基本假設是樣本中包含正確數據也包含異常數據，即數據集中含有噪聲。這些異常數據可能由于錯誤的測量、錯誤的假設、錯誤的計算等產生。同時RANSAC也假設給定一組正確數據，存在可以計算出符合這些數據模型參數的方法[12-13]。它是一種有效的參數估計算法，通過不斷迭代，從包含內點和外點的觀測數據集中隨機選取一定數量的樣本對單應性矩陣進行估計，最終找出內點個數最多、誤差最小的單應性矩陣。RANSAC算法的最小迭代次數如下：

其中，[ε]是內點在觀測數據集中的比例，n是得到模型參數所需要的最少樣本數，p代表置信度，一般取0.95[～]0.99。計算兩幅圖像的單應性矩陣所需的最少樣本數n=4，置信度取p=0.97。因為內點數在數據集中的比例通常未知，所以通常選擇最壞條件下的內點比例，之后通過不斷更新此內點比例進行迭代。

SIFT算法是一種數字圖像特征描述常見的算法，這種描述具有尺度不變性，可在圖像中檢測出關鍵點，提取位置、尺度、旋轉不變量。通過傳統SIFT算法提取兩幅圖像的特征點后，采用歐式距離作為特征點進行相似性度量[14]。雖然采用兩個特征點之間的歐氏距離進行特征匹配的方法簡單快捷，但難免會存在一些在尺度空間上特征比較相似的誤匹配點。因此，需要采用RANSAC算法去估計兩幅圖像之間的單應性矩陣，然后再利用單應性矩陣剔除誤匹配點[15]。

RANSAC算法步驟如下：①從初始匹配對集合S中隨機選取4對匹配特征點作為內點集合Si，估計初始的單應性矩陣Hi;②用Hi計算S中剩余的匹配點對。如果某個特征點的投影誤差小于閾值t，則將其添加到Si中;③記下Si集合中匹配點對的數量;④重復以上步驟，直到迭代次數大于k;⑤比較哪次計算中內點數量最多，內點數量最多的那次估計模型就是所要求解的單應性矩陣。

2 改進RANSAC算法的單應性矩陣估計方法

傳統的RANSAC算法主要存在兩個局限性[16]：①效率。傳統方法效率與子集大小、內點比例以及數據集大小有關。當數據集中存在較多的誤匹配點時，需要增加迭代次數，同時大量錯誤的單應性矩陣內點檢測會降低運算效率;②精度。傳統方法在計算單應性矩陣參數時，為了考慮效率，通常選取最小子集去估計模型參數，所以得到的模型參數并非最佳參數。

本文從3個方面對RANSAC算法加以改進：

（1）利用特征點周圍灰度值的相似性進一步剔除誤匹配點。在兩幅待拼接圖像中，兩對正確的特征點匹配對周圍灰度值的變化應該具有很高的相似性，根據這一特性將初始匹配點按照灰度梯度變化的相似性從大到小依次排序，并將前80%的特征點匹配對作為求參點集，進一步剔除誤匹配點，從而減少單應性矩陣估計的迭代次數。本文采用8鄰域的拉普拉斯算子計算特征點周圍灰度值的梯度變化，具體公式如下：

其中step為步長，在本文中step=1。

（2）快速舍棄錯誤的單應性矩陣以減少內點檢測時間。在每次隨機選取4個匹配點去估計初始單應性矩陣后，即使單應性矩陣不合理，也需要測試剩余的所有匹配點對，這大大增加了計算量。所以，本文利用初始單應性矩陣在剩余匹配點對中隨機選取4對匹配點，如果這4對匹配點均適合該單應性矩陣，則加入到內點集中繼續進行匹配操作，如果其中有任意一個匹配點對不符合該單應性矩陣，則馬上舍棄該單應性矩陣，重新選取新的匹配點對去估計新的單應性矩陣。本方法可以快速舍棄不合理的單應性矩陣，從而大大減少單應性矩陣測試所有剩余匹配點對的時間。

（3） 在應用機器學習算法時通常都會使用梯度下降法去訓練模型參數，因此本文將采用批量梯度下降法（Batch Gradient Descent，BGD）進一步精確擬合單應性矩陣參數，投影變換矩陣如下：

由式（3），把一個圖像中的[x，y，1]作為訓練單應性矩陣H的輸入數據，把另一個圖像中的[x，y，1]作為[x，y，1]對應的標簽數據，因此特征點匹配對作為訓練單應性矩陣H的訓練數據集。將之前由RANSAC算法獲得的單應性矩陣H的值作為訓練時的初始值，因此能夠在極短的時間內使得損失函數收斂，獲得精確的單應性矩陣。

BGD算法的具體思路是，在更新每一參數時都使用所有樣本進行更新。假設單應性矩陣H中的每個參數為[θj]，則線性回歸的假設函數為：

其對應的損失函數為：

其中，n=9，m是由RANSAC算法得到的最多內點個數。

對損失函數求偏導可得：

最小化損失函數需按照每個參數[θ]的梯度負方向更新每個[θ]值：

其中[α]為學習率，它控制[θ]每次向[Jθ]變小的方向迭代時的變化幅度。[α]屬于超參數，多次實驗結果表明，[α]取0.01時能夠使損失函數快速收斂并不發生局部振蕩現象。

通過上述公式可知該算法能得到一個全局最優解，損失函數接近最小值時單應性矩陣精度也最高。

3 實驗與分析

通過金相顯微鏡采集一組一元硬幣中“YI”字符局部的顯微圖像，如圖1所示。表1為顯微鏡采集環境，采用傳統RANSAC算法和改進RANSAC算法作對比實驗，驗證改進RANSAC算法的正確性。

首先使用SIFT-PCA算法提取圖1（b，c）中的特征點，圖 1（b）的特征點個數為3 685個，圖1（c）的特征點個數為2 087個;然后采用近似最近鄰搜索算法按照R=0.6進行初始匹配。初始匹配的特征點個數為220個，如圖2 所示，從圖2可以看出初始匹配后的圖像中存在大量誤匹配點。

圖2 初始匹配后的特征點匹配對

在初始匹配基礎上，分別采用傳統RANSAC算法和改進后RANSAC算法估計單應性矩陣，并利用單應性矩陣剔除圖像中存在的誤匹配點對，式（8）、式（9）分別是傳統RANSAC算法的匹配結果和改進RANSAC算法的匹配結果。從式（8）可以看出，傳統的RANSAC算法仍出現了少量誤匹配，需要進一步剔除，而采用改進后的RANSAC算法能夠進一步剔除誤匹配和一些特征點匹配度較弱的匹配點。利用改進RANSAC算法估計出的單應性矩陣進行透視投影變換，將右圖與左圖拼接，拼接結果圖3 所示。

傳統RANSAC算法的特征點匹配結果及傳統RANSAC算法的單應性矩陣如下：

改進RANSAC算法的特征點匹配結果及改進RANSAC算法的單應性矩陣如下：

為驗證改進RANSAC算法在估計單應性矩陣精度和運行時間上的優越性，本文采用均方根誤差（RMSE）作為幾何誤差，將特征點匹配準確率作為評價指標。

其中，S是剔除誤匹配后的匹配點個數，H是單應性矩陣，[pi]是待匹配圖1中的某一點坐標，[qi]是待匹配圖2中的某一點坐標，[Hqi]為[qi]通過單應性矩陣H轉換到圖1中的對應坐標點，dis代表歐式距離。

理論上在單應性矩陣H非常精確的情況下，坐標點[qi]與[Hqi]應該重合，即幾何誤差RMSE=0。但RMSE一般是一個不為零的數，并且RMSE越小，估計的單應性矩陣H的精度越高。由于RANSAC算法是隨機選擇內點進行參數模型估計的，因此本文統計5組實驗結果。

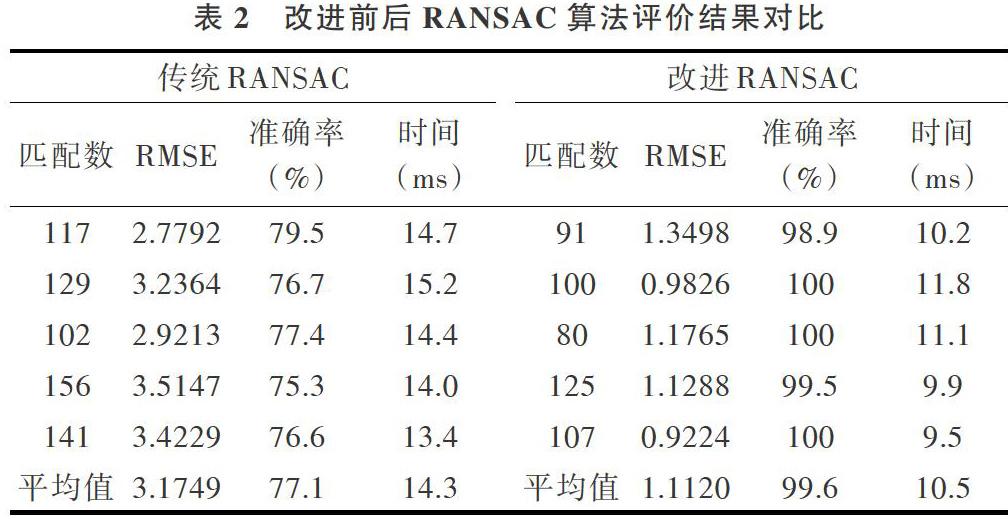
在計算特征點匹配準確率時需要確定一個誤差閾值，也就是說[dis（pi，Hqi）]的值小于某個誤差閾值時，可以判定這對特征點匹配正確。根據Krystian Mikolajczyk在《An affine invariant interest point detector》一文中對誤差閾值的設定可知，特征點檢測器實際上檢測的是特征區域，例如Harris-Affine檢測的是一個橢圓區域，SIFT檢測的是一個圓形區域，因此，當兩個特征點區域的重疊誤差小于1.5個像素時，則可判定這是一對正確匹配的特征點。根據實驗結果選取重疊誤差閾值為2，實驗結果如表2所示。

從表2可以看出，改進的RANSAC算法相比于傳統的RANSAC算法能夠大大提高單應性矩陣精度，降低了內點檢測時間，提高了執行效率，從而驗證了改進RANSAC算法的正確性和有效性。為驗證本文提出的改進RANSAC算法的魯棒性，將其應用到多視野拼接過程中。圖4為“YI”字符的圖像序列，共采集相鄰的10個視野，拼接結果如圖5所示。從圖5可以看出，拼接圖像無錯位現象，且沒有發生明顯的扭曲變形，從而進一步驗證了本文算法的魯棒性和精確性。

4 結語

本文針對RANSAC算法存在迭代次數多、運行時間長、估計的單應性矩陣精度低等問題，提出一種基于改進RANSAC算法的單應性矩陣估計方法。利用特征點周圍梯度變換的相似性剔除初始匹配中的部分誤匹配點，通過快速舍棄錯誤的單應性矩陣，以減少內點檢測時間;通過BGD算法最小化損失函數進一步擬合精確的單應性矩陣。實驗結果表明，改進的RANSAC算法能大大提高單應性矩陣精度，減少運行時間，提高算法執行效率。但本文對于需要設置與問題相關的閾值t沒有進行深入研究，未來的工作是進一步考慮閾值t對算法運行效率和單應性矩陣精度的影響。

參考文獻：

[1] 陸園園， 張明. 基于SIFT算法的紅外圖像拼接方法改進[J]. 計算機系統應用，2015，24（8）：165-170.

[2] DUAN Y，CHEN W，WANG M，et al. A relative radiometric correction method for airborne image using outdoor calibration and image statistics[J]. IEEE Transactions on Geoscience and Remote Sensing， 2014， 52（8）：5164-5174.

[3] 王俊杰，劉家茂，胡運，等. 圖像拼接技術[J]. 計算機科學， 2003，30（6）：141-144.

[4] 伍夢琦，李中偉，鐘凱，等. 基于幾何特征和圖像特征的點云自適應拼接方法[J]. 光學學報，2015，35（2）：237-244.

[5] 蔣波，翟旭平. 基于PCA-SIFT特征匹配的圖像拼接算法[J].? 計算機應用，2016， 36（s2）：143-145.

[6] MA Y，REN Z. Image mosaic method based on improved sift feature detection algorithm[C].? Proceedings of the 9th International Symposium on Linear Drives for Industry Applications，2014：771-779.

[7] 雒偉群，高屹. 基于改進RANSAC算法的圖像拼接方法[J]. 科技創新與應用，2015（5）：21-22.

[8] 趙輝， 陳輝，于泓. 一種改進的全景圖自動拼接算法[J]. 中國圖象圖形學報，2018，12（2）：336-342.

[9] 熊飛雪. 基于改進的RANSAC算法的圖像拼接研究[D]. 阜新：遼寧工程技術大學，2016.

[10] 周劍軍，歐陽寧，張彤. 基于 RANSAC 的圖像拼接方法[J]. 計算機工程與設計，2009，30（24）：5692-5694.

[11] 劉婷婷.? 基于單應性矩陣剔除SIFT錯誤匹配點的方法[J]. 哈爾濱商業大學學報：自然科學版，2016，32（1）：95-98.

[12] 王淑霞，周波. 一種基于RANSAC算法的單應矩陣估計方法[J]. 科學中國人，2015 （8Z）：157-161.

[13] 單欣，王耀明，董建萍. 基于RANSAC算法的基本矩陣估計的匹配方法[J]. 上海電機學院學報，2006，9（4）：66-69.

[14] 瞿中，李秀麗. 基于改進IGG模型的全景圖像拼接縫消除算法[J]. 計算機科學，2017，44（12）：274-278.

[15] MOU W，WANG H，SEET G. Robust homography estimation based on nonlinear least squares optimation[J]. Mathematical Problems in E-ngineering，2014（6）：372-377.

[16] 劉曉霞，李峰，熊兵. 基于韋伯局部特征的圖像拼接檢測[J]. 計算機工程與應用，2013，9（12）：140-143.

（責任編輯：杜能鋼）