基于傅里葉級數殘差修正TDGM（1，1）的車流量預測模型

劉素娟

摘要：車流量預測是城市智能交通研究中的熱點和難點問題之一。然而，車流量受到諸多因素的不同程度的影響，使用單一模型難以對其進行準確預測。針對這一問題，本文提出了基于傅里葉級數殘差修正TDGM（1，1）的車流量預測模型。該模型首先應用離散灰色模型TDGM（1，1）對原始車流量序列進行建模，并得到初始預測值以及殘差序列;然后通過傅里葉級數對殘差序列進行二次擬合，同時對預測結果進行修正。通過實例分析以及對比試驗表明，該模型可以有效提高車流量預測精度。

Abstract： Traffic flow prediction is a key problem in urban transport system. However， many complicated factors have impact on the traffic flow prediction， which means that single model can not be used to forecast the traffic flow correctly. Aiming at this issue， a combined residual modification TDGM（1，1） model based on Fourier series is proposed for predicting the traffic flow. Firstly， this model used the TDGM（1，1） model to predict the original series of the traffic flow， and obtain the initial predicted values and the corresponding residuals. Then the Fourier series were introduced to modify the residual series and get the final predicted values. The experiments demonstrated that， in comparison with the common methods， the residual modification TDGM（1，1） model based on Fourier series can improve the prediction accuracy effectively.

關鍵詞：車流量預測;離散灰色模型;傅里葉級數;殘差

0? 引言

交通是一座城市的命脈，是城市活力與可持續發展的重要支撐。最大限度地利用道路資源，提高交通運輸效能，對道路的車流量進行準確、快速的預測是當前智能交通系統發展的重要任務[1，2]。

影響車流量的因素眾多、關系復雜，具有灰色特征，可以采用灰色系統理論對其進行預測。根據灰色系統理論對車流量預測時，主要以灰色模型GM（1，1）及其改進模型為主[3]。GM（1，1）模型是灰色系統模型中的核心和基礎，它在有限數據的情況下有著較好的預測精度，在各個研究領域得到了廣泛的應用，但仍然存在很多需要改進的問題：即可以在一定程度上降低模型擬合誤差、提高預測精度，但卻無法改變GM（1，1）模型本身的局限性，即利用離散方法去估計模型參數，而采用連續時間響應函數進行預測所造成的跳躍性誤差。與GM（1，1）模型相比，離散灰色模型DGM（1，1）有效地避免了從離散到連續模型轉換所帶來的誤差，其具有白指數規律重合性、伸縮變換一致性等性質[4]，但也存在模擬值只能為等比序列的問題。線性時變參數離散灰色模型TDGM（1，1）除了具有白指數規律重合性、伸縮變換一致性等性質外，還具有線性規律重合性的性質[5，6]，從而克服了離散灰色模型DGM（1，1）模擬值增長率恒定的問題。另一方面，在車流量預測過程中，線性時變參數離散灰色模型TDGM（1，1）只對車流量呈近似指數規律的單調增長序列才有較高的預測精度。但車流量的波動性將在一定程度上影響TDGM（1，1）的擬合和預測效果，因而對TDGM（1，1）進行修正是十分必要的。

針對這一問題，本文將應用傅里葉級數殘差修正方法對TDGM（1，1）模型進行改進，以提高車流量預測性能。同時，結合實際車流量數據對基于傅里葉級數殘差修正的TDGM（1，1）模型進行分析，驗證模型的有效性和可行性。

1? 線性時變參數離散灰色模型TDGM（1，1）模型

基于傅里葉級數殘差修正TDGM（1，1）模型的車流量預測方法，首先應用線性時變參數離散灰色模型TDGM（1，1）對原始車流量序列進行建模，并得到初始預測值以及殘差序列;然后通過傅里葉級數對殘差序列進行修正，并獲得最終的車流量預測結果。

3? 算例檢驗

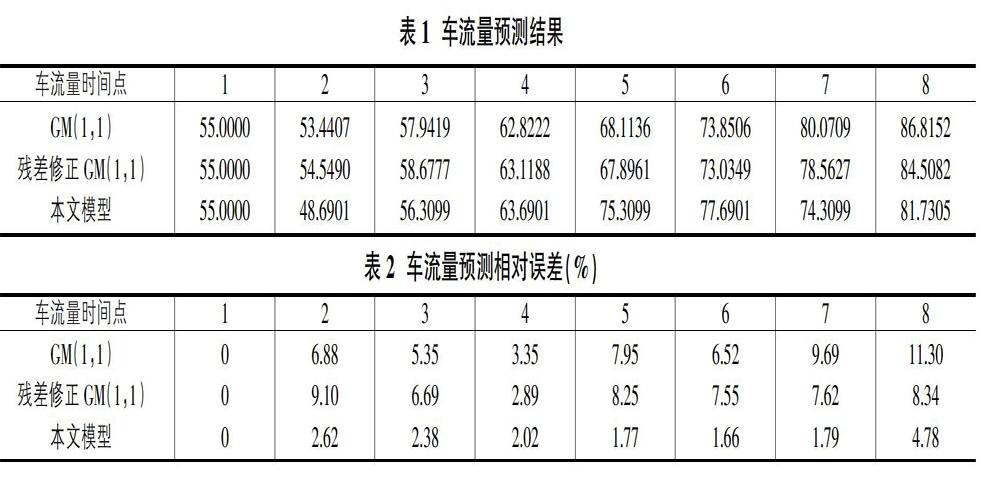
為了檢驗本文提出的基于傅里葉級數殘差修正TDGM（1，1）的車流量預測模型，本節根據文獻[7]中的車流量數據進行比較和分析。實驗所用車流量序列如下：55、50、55、65、74、79、73、78，其中每項代表5分鐘內通過監測點的車輛數。根據前7個數據建立傅里葉級數殘差修正的TDGM（1，1）模型，并對第8個數據進行預測，預測結果如表1所示。此外，為了便于對比分析，表1也同時給出了應用GM（1，1）模型、以及基于殘差修正的GM（1，1）模型的預測結果。根據表1，計算出三種方法的相對預測誤差如表2所示。

從表2可知，對于第8個預測數據，相對預測誤差分別為11.30%、8.34%以及4.78%，本文模型的預測效果要優于經典GM（1，1）模型以及基于殘差修正的GM模型。即對于車流量預測而言，本文提出的基于傅里葉級數殘差修正TDGM（1，1）模型是合理可行的。

4? 結論

本文提出了基于傅里葉級數殘差修正TDGM（1，1）模型的車流量預測方法，該模型應用線性時變參數離散灰色模型TDGM（1，1）對原始車流量序列進行建模，并得到初始預測值以及殘差序列;然后通過傅里葉級數對殘差序列進行修正，并獲得最終的車流量預測結果。實例表明，本文模型可以有效提高車流量預測精度。

參考文獻：

[1]刁仁群，王偉，李劍.“互聯網+交通”背景下交通大數據應用分析[J].交通企業管理，2017（04）.

[2]趙文天，萬夕里，白光偉.城市交通流量預測與信號控制優化[J].小型微型計算機系統，2019（07）.

[3]李夢婉，沙秀艷.基于GM（1，1）灰色預測模型的改進與應用[J].計算機工程與應用，2015（09）.

[4]王豐效.線性時變參數DGM（1，1）變權組合預測模型[J].統計與決策，2017（13）.

[5]田英俊，宋立忠，阮苗鋒.基于線性時變參數離散灰色模型的在線故障預測系統設計[J].海軍工程大學學報，2018（01）.

[6]易梅，高雅萍，郭瑞雪，張文靜，徐濤.動態殘差修正的新陳代謝灰色模型在沉降預測中的應用[J].工程勘察，2018（04）.

[7]趙卓峰，楊宗潤.基于殘差修正GM（1，1）模型的車流量預測[J].計算機科學，2017（4）.