基于前景理論的集裝箱海鐵聯運定價與運營決策

高智源

摘 要：由于客戶很難做到對市場信息的完全掌握，本文引入前景理論的情況下，基于運營商與客戶的互動性，建立了雙層規劃模型。通過集裝箱海鐵聯運的定價博弈分析，得出運價優化模型。基于運價設計了班列運營模型，以利潤最大為目標，設計啟發式算法求解。為提高集裝箱海鐵聯運的競爭力，基于有限理性客戶的選擇行為，本文為鐵路運營商進行了集裝箱海鐵聯運定價與班列運營的協同優化。

關鍵詞：海鐵聯運;班列運營;定價;前景理論

目前我國海鐵聯運固定運價的價格機制不能適應目前市場化的競爭環境，也不利于鐵路運輸企業的收益。鐵路運輸企業必須建立以市場需求為導向的靈活的定價機制。此外，集裝箱班列開行和停靠決策仍然缺乏科學合理的制定機制。客戶需求決定了開行方案，集裝箱班列的開行方案又關系到運輸時效性，而運輸服務的價格和時效性又對客戶需求產生影響。開行方案與定價之間互相影響，有必要對兩者進行綜合研究。

運輸領域定價優化問題方面，國內外學者選擇了不同的角度和方法理論作為研究依據和方向，有收益管理、動態定價、競爭博奔定價、風險價值VAR研究以及基于金融衍生品的定價等。張玥[1]等對現行的鐵路貨運運費定價方式做出了總結，并且提出差別定價法，通過模型優化提高利潤。殷明[2]等利用經典的二部定價法，基于單個箱子總質量去優化集裝箱班輪的定價，并且通過這個模型使班輪公司的利潤增長了20%。顧鋒[3]等研究了雙寡頭壟斷市場中的兩個企業的定價均衡和選址決策問題，并且他們的產品質量不同，消費者可以任意選擇。Li Li[4]等研究對象為美國的某鐵路運輸公司，利用實際的市場數據，將服務分為兩個等級，分別做定價，同時優化了開行班列的路線網絡，以利潤最大作為目標函數，得出最優的兩個等級的價格和班列網絡路線。Figliozzi M A[5]等主要研究了針對一種拓展型的TSP路徑優化問題提出承運人定價的最優決策問題，并且這種情況是動態的，需要等到客戶到來的時候才知道要提供哪一種類型的服務。

班列安排方面或路徑優化方面，研究目標主要包括班輪和班列的總成本最小。彭其淵[6]等分析集裝箱在結點站集結過程中的到達情況，利用隨機概率的理論原理，建立以節點站集裝箱班列集結時間最小為目標函數的數學模型。Wang W F[7]等考慮了時間窗，研究了進、出口箱以及重、空箱這四種集裝箱應該如果選擇運輸方案，即火車還是集卡實現客戶與港口之間的運輸，使得效率最高、成本最小。Newman A M[8]等設計了算法優化出在多式聯運中火車班列路徑安排，其中考慮到了直達的班列和中轉的班列。

1 基于前景理論的運價優化模型

客戶決策行為研究大都是基于Von Newmann和Morgenstern提出的期望效用理論。期望效用理論建立于客戶基于完全理性進行決策的假設之上，并依據效用最大化理論來得出最優的決策。但是，在兩種集裝箱運輸方式并存于內陸，鐵路運輸、公路運輸的箱量分擔率大小決定于客戶的決策行為，屬于群體多目標決策問題。影響客戶群體決策的因素既包括運輸方式的技術經濟特征，也包括客戶個人偏好等因素，除此之外，還存在不確定的隨機影響因素。客戶群體在選擇集裝箱運輸方式時，已知的信息并不準確和全面，決策主體的分析和計算出行效用的能力也并非達到統一的標準，因此，很難做到完全理性。Simonpy于1947年提出了“有限理性”的理論，認為決策者不可能獲取及時、完整、準確的信息來支持其做出合理決策。為了刻畫對客戶真實決策行為，Kahneman Tversky提出了前景理論，進一步解釋了部分依據期望效用理論所無法得出結論的“異象”。前景理論具有以下特征：（1）依賴于參照點的選取：客戶決策時會預設一個參照點，并通過參照點來衡量結果為收益或損失;（2）客戶風險偏好轉變：客戶風險偏好會在參照點附近發生逆轉，收益時傾向于風險厭惡，損失時傾向于風險追求。

假設港口和目的城市分別為O點和D點。OD之間存在的鐵路與公路兩種集裝箱運輸方式，分別可抽象為兩條路徑（路徑1路徑-1）。在這里假設客戶只對集裝箱運輸方式的運輸時間和運輸費用成本兩個影響因素顯著敏感。? ?表示運輸方式? ?對客戶的運輸效用，效用的均值和方差分別? Kahneman和Tversky將人們的決策過程分為編輯和評價兩個階段：在編輯階段，決策者將決策的各種可能結果編輯為相對于某個參照點的收益或損失;在評價階段，決策者依據價值函數對收益和損失進行主觀評價，并依據決策權重函數測度主觀概率風險。Kahneman和Tversky給出的價值函數和決策權重函數形式分別如下：

在鐵路和公路的博弈優化模型中，不僅要包括上層決策制定者，即運輸運營商，也要包括定價決策的受眾即客戶，他們共同作用在這一動態博弈過程中。因此，為了更好地刻畫此博弈過程，本文引用雙層規劃模型。雙層規劃模型分上層規劃和下層規劃，分別代表上層兩種運輸方式運價決策和下層客戶的決策行為過程。

OD兩地同時存在鐵路與公路兩種集裝箱運輸方式，上層決策者分別是鐵路運營商和公路運營商。兩種集裝箱運輸方式制定運價時均會以自身運營利潤最大化為目標，還通過預測競爭對手的運價來調整自身運價，在不斷循環后，當鐵路與公路任一方再調整決策時也不存在更優的利潤時，即二者達到廣義納什均衡。

下層規劃的參與者也就是客戶，通過改變集裝箱運輸方式來達到最小化廣義運輸費用，致力于最經濟便捷的運輸方式完成集裝箱運輸。

基于前景理論的集裝箱運價優化模型如下：

2 給定運價下的班列運營優化模型建立

基于定價博弈分析，根據以往研究已證明的納什均衡解存在性，可以對給定運價下的運輸需求進行了班列運營方案的設計。在基于市場需求與價格，以利潤最大為目標，以班列運營利潤最大為目標函數，建立了給定運價下的班列運營模型。已知到港箱目的地以及到達時間的情況下，為了實現鐵路經營人利潤的最大化，需要進一步優化集裝箱到達中心站后應該如何安排班列的行駛路線、發班時間以及發班次數。

2.1模型假設

（1）本文僅研究單向行駛的班列，即從港口中心站裝箱出發，到各個內陸目的城市卸箱的問題情景;

（2）假設集裝箱到達中心站時間服從泊松分布，到達時間間隔服從指數分布;

（3）假設每個目的城市之間都通過鐵路相連;

2.2符號定義

I：班列掛靠城市的集合，其中i，j∈I表示城市編號

qi：目的地為城市的集裝箱數量

R：班列的路線集合，r∈R為子路線

C：一周之內到達港口，并通過海鐵聯運運輸的集裝箱集合，其中 c∈C表示集裝箱編號

p：班列運輸單位集裝箱單位距離的運價

h：單位集裝箱的裝卸成本

RCi：班列在城市i的管理費成本

dij：城市i到城市j之間的運輸距離

eij：城市i到城市j單位距離的在途運輸成本

Qmax，Qmin：班列單列的最少、最大運載箱量

Tc：集裝箱c到達集裝箱中心站的時刻

2.3 模型建立

運營成本包括在途運輸成本TC、在站管理費成本RC、裝卸成本HC以及客戶平均等待成本AWT。

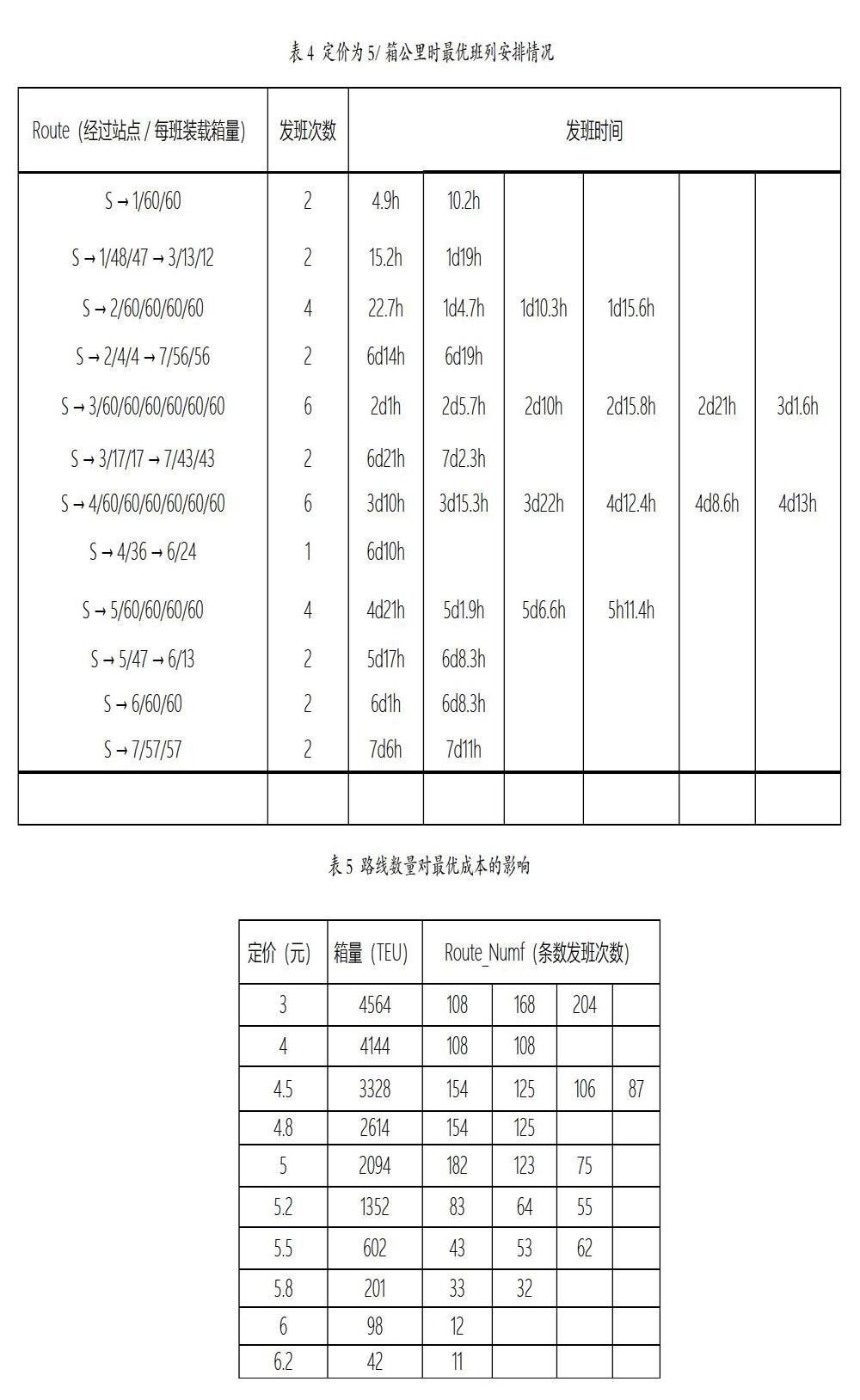
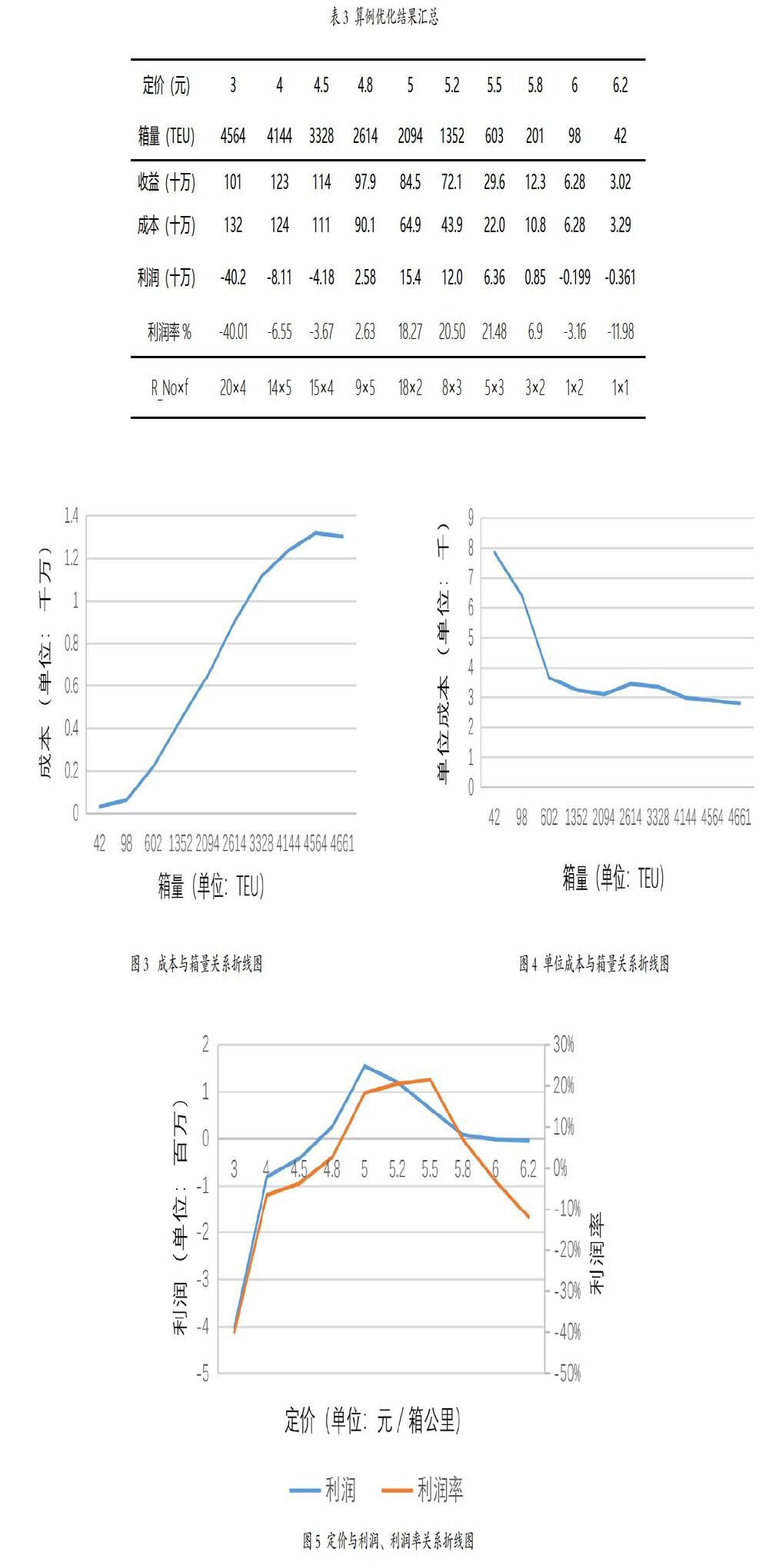
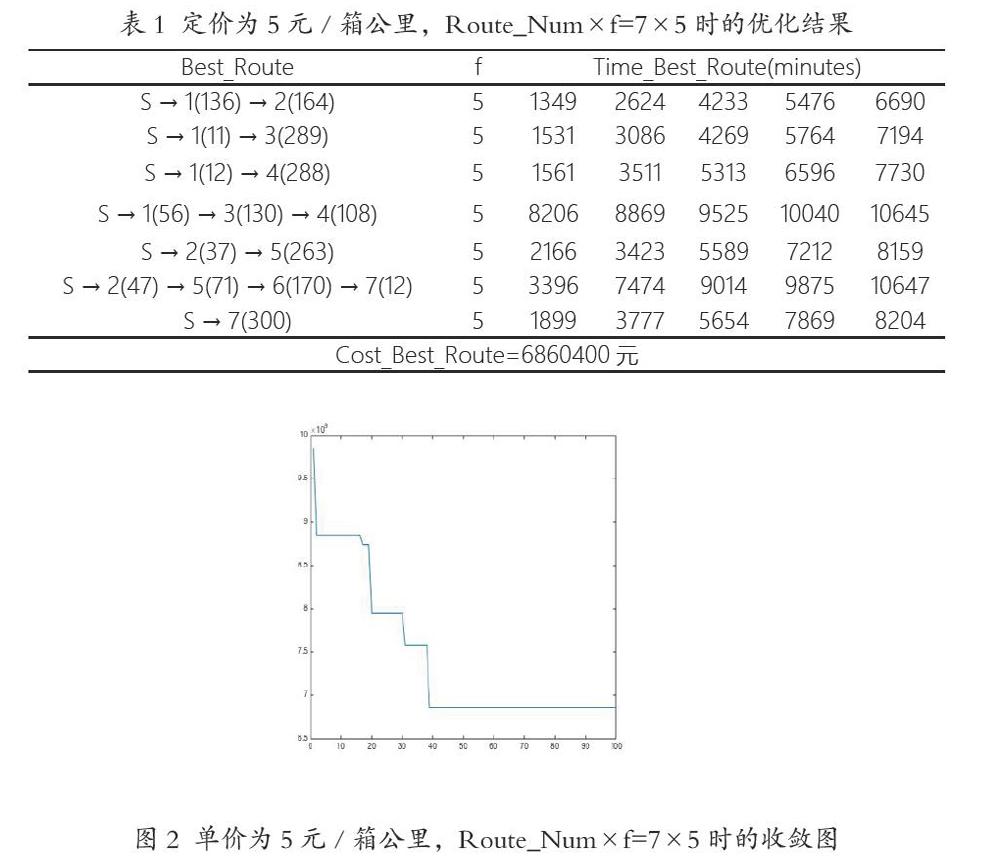
其中，i，j表示路線r上任意相鄰的兩個城市，i

目標函數為班列利潤最大，因此建立模型如下：

對每輛班列載重量作出限制：

使每個城市需求量都能夠滿足：

一個集裝箱只能選擇某一輛班列進行運輸：

班列的發班時間晚于裝上該輛班列的集裝箱中最晚到達中心站的時間，路線? ? ? ? ? ? ?經過所有站的集合是

3 算法設計

假設在集裝箱到港時間以及目的地信息已知的基礎上，進行班列路徑方案的設計，具體算法如圖1：

4 算例分析

在給定運價水平下，即5元/箱公里，獲得的市場份額為2094個箱子，假設每趟火車都裝滿，即每趟車都裝60個箱子，那么最少需要35趟車。只考慮最接近35的數字乘積組合，那么總共有三組線路和次數的組合，即第一，18條子線路，每條子線路次數最多為2，即每條子線路最多裝120個箱子;第二，12條子線路，每條子線路次數最多為3，即每條子線路最多裝180個箱子;第三，7條子路線，每條子路線次數最多為5，即每條子線路最多300個箱子。同時需要排除某條線路出現裝箱量為1到40個，或者60到80個的路線組合，因為在這個范圍內的路線都不符合單趟火車最少裝40個箱子的要求。

用Matlab按照上章所述步驟設計程序計算，最后得出最小成本的路線組合以及利潤率。

還是以上述例子為基礎，以第三種線路數和次數的組合方式為例，即7條子線路，每條子線路發班次數最多為5時，優化出來的結果如表1所示。

因此此刻盈利為8449964.5-418800-6860400=1170764.5元，收益率為1170764.5/8449964.5*100%=13.86%。同理，定價為5時的其他路線和次數組合情況也是以同樣的方式計算，最后對比得出成本最低的組合為最優組合。其余算例同理，下表設定了在不同定價下的箱量，以及有待優化的情況：

4.4 結果分析

上一節所列舉出來的有待優化的情況，經過優化后，數據匯總如表3：

從圖3看出，成本則是隨著定價的增加而減少，或者換句話說即隨著箱量的減少而減少，這也是符合邏輯的，因為箱子規模增加直接導致運營成本增加，箱量減少，營運的成本也減少。但是可以看出成本的增加幅度會隨著箱量增加而下降，因此托運越多的箱子，單位成本越低，相反，則越高，如圖4。

值得討論的是定價和利潤以及利潤率的關系，通過這個可以直接判斷出來，哪一個范圍內的定價是最優的，能使得整體的盈利最高。如下圖為三者之間的關系：

可以通過圖看出在該算例中，可以根據自己的戰略選擇在4.8和5.5之間定價，可以獲得較為良好的業績結果。如果選擇利潤最高的定價，即5元/箱公里，應該如下安排班列運輸：

在火車總數量一定的時候，即Route_Numf數一定的時候，子線路數量越多，即Route_Num越大，優化成本就越低。具體可見表5。

5結論

當前海鐵聯運處于?力發展的階段，而現在集裝箱鐵路運輸的薄弱競爭力成了海鐵聯運的瓶頸，使得集疏運由公路運輸承擔，不利于集裝箱多式聯運的發展，也妨礙港口作業水平的提升。因此本文站在鐵路運輸經營人的角度，提出了包括集裝箱海鐵聯運定價和班列運營方案在內的決策模型。基于有限理性的客戶決策行為的分析，再運用雙層規劃模型得到最優的定價，之后基于給定運價設計最優的班列運行方案，使得鐵路經營人達到利潤最大。

參考文獻：

[1] 張玥. 區域鐵路貨運差別定價研究[D]. 西南交通大學， 2014.

[2] 殷明， 盛子寧， 丁以中，等. 基于單箱總質量的集裝箱班輪二部定價模型[J]. 交通運輸工程學報， 2010（3）：101-109.

[3] 顧鋒， 薛剛. 存在消費者購買選擇的企業定價選址模型[J]. 系統管理學報， 1999（4）：32-37.

[4] Li L， Tayur S. Medium-Term Pricing and Operations Planning in Intermodal Transportation[J]. Transportation Science， 2005， 39（1）：73-86.

[5] Figliozzi M A， Jaillet P. Pricing in Dynamic Vehicle Routing Problems[J]. Transportation Science， 2007， 41（3）：302-318.

[6] 彭其淵， 閆海峰， 周勇. 集裝箱班列編組計劃相關因素分析[J]. 中國鐵道科學， 2003， 24（5）：120-123.

[7] Wang W F， Yun W Y. Scheduling for inland container truck and train transportation[J]. International Journal of Production Economics， 2013， 143（2）：349-356.

[8] Newman A M， Yano C A. Centralized and decentralized train scheduling for intermodal operations[J]. Iie Transactions， 2000， 32（8）：743-754.