主導風向對不規則建筑群街區污染物擴散的影響*
戰乃巖 呂 廣 高 政 張 帥 李 進 金陶勝
(1.吉林建筑大學市政與環境工程學院,吉林 長春 130118;2.吉林省建苑設計集團有限公司,吉林 長春130011;3.南開大學環境科學與工程學院城市交通排放研究中心,天津 300350)
隨著我國城市交通保有量不斷上升,污染物排放日益嚴重。同時,隨著建筑群密度劇增,道路兩側建筑物與街道形成眾多“街道峽谷”[1],勢必影響交通污染物的擴散,嚴重影響過往行人的健康。來流風對污染物擴散的影響不容忽視,不同城市主導風向差異很大,若能有效利用主導風向,勢必能有效控制街區污染物的危害程度。
針對城市街谷交通尾氣污染物擴散問題,國內外學者采用數值模擬和風洞試驗等手段已做了一些研究。徐偉嘉等[2]研究了街道峽谷內有兩車道時的流場與污染物濃度場,結果表明:不同車道位置對街谷底部污染物擴散有較大影響;在道路兩側設置綠化帶使車道置于街道峽谷中央,可有效改善空氣品質。李志遠等[3]測量了高架下街谷內可吸入顆粒物擴散的狀況,結果表明,街谷內沿高度方向可吸入顆粒物濃度先逐漸減小,超過高架路面高度后突增。劉慧等[4]采用風洞試驗對某城區典型路段的流場和污染物濃度分布展開研究,結果表明:模擬和風洞試驗在采樣點處污染物濃度的相對誤差較小,變化趨勢近似相同;豎直高度越高氣流速度增大趨勢越明顯,受其影響污染物濃度下降的趨勢越明顯。WANIA等[5]研究了綠化帶對街道峽谷內顆粒物擴散的影響,研究發現,綠化帶的存在影響到街道峽谷內顆粒物的擴散趨勢,當有綠化帶時顆粒物不易擴散稀釋。XIE等[6]現場測量了街道峽谷交通污染物的空間分布,研究表明,機動車排放污染物濃度與交通量變化、風向和風速等具有一定的相關性。
綜上,大多數研究多是針對較規則建筑布局下的街道峽谷,忽略了城市道路和建筑的復雜性對道路環境的影響,且主導風向對污染物擴散影響問題分析不詳細。因此,本研究以城市道路某段典型的街道峽谷為研究對象,采用ICEM CFD數值模擬技術,分析不同風向對不規則建筑群街區污染物擴散影響,為街區污染物的有效控制提供一定的理論依據。
1 物理和數學模型
1.1 物理模型
街區物理模型如圖1所示,街道峽谷區域尺寸為860.0 m×480.0 m,X軸正向為北向,Y軸正向為西向。街區包括4條街道(A、B、C、D),其中東西方向的街道B為主干道,路寬45.0 m,其余3條為支路,路寬40.0 m,街道形成一個“十”字路口和兩個方向相反的“T”型路口。將街谷內交通污染源看作連續發散的線污染源,位于街谷正中間,其寬度×高度為20.0 m×0.5 m。為保證來流充分發展,避免計算域過小引起端部效應,造成計算結果出現偏差,計算域設置X、Y、Z軸向距離為2 780.0 m×2 260.0 m×600.0 m的空間,符合CFD軟件應用要求[7]。
選擇ICEM CFD對三維模型進行網格劃分,采用結構化網格進行劃分難以實現,因此采用四面體非結構化網格對長方體模型進行劃分。這種網格的適應性較好,更易于計算域劃分和網格加密。為提高核心研究區域的計算精度,對建筑群表面和街道等位置進行局部網格加密,不存在負體積出現,網格質量滿足計算要求,證明網格不存在畸變的問題,網格質量良好,對后續數值計算結果影響很小,不會產生數值計算結果突變的問題。網格總數為9 900 000,網格節點為1 600 000個。
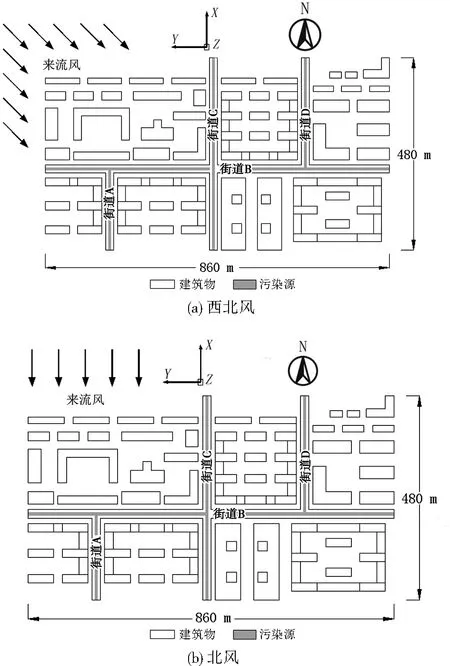
圖1 物理模型
1.2 數學模型
利用ICEM CFD數值模擬進行污染物擴散研究,涉及的物理模型包括Navier-Stokes方程、連續性方程、E-ε方程及污染物擴散模型。Navier-Stokes方程考慮了地球偏轉力、浮力的影響,采用三維非靜力不可壓縮流體模式求解風場。而污染物擴散涉及流體流動,需應用連續性方程[8-9]。氣流在墻體表面出現氣流速度剪切時會產生湍流,湍流動能及其耗散率被用來計算大氣湍流的變化率[10-11]。污染物擴散方程基于顆粒物和氣體在大氣中和表面上的動力學經典原理[12-13]。
1.3 邊界條件
計算域內流體為空氣和污染氣體CO,兩者均為非定常流體,因此將計算域入口條件設置為速度入口,使用FLUENT自帶的用戶自定義函數(UDF)設定速度輪廓線,入口氣流速度采用指數型速度邊界條件(見式(1))[14]。出口邊界遠離街區,故將邊界條件設為自由出流。計算域地面及建筑物壁面設置為無滑移邊界條件。兩側邊界和上邊界設置為對稱邊界,即沒有對流通量和擴散通量。CO是城市街區中重要的標識性污染物,其主要來源是城市交通工具的排放,在一般的近地環境中,CO相對穩定并不易與其他氣體發生化學反應,故選擇CO作為汽車尾氣排放物[15],將CO散發源條件設置為恒定發散,排放源強度為0.000 014 kg/(m3·s)。
Uz=U10(z/10)μ
(1)
式中:Uz為距離地面z高度處的氣流速度,m/s;U10為距離地面10.0 m高處的氣流速度,m/s,取2.0 m/s;z為Z軸方向距離(即距離地面高度),m;μ為地面粗糙系數,取0.3。
2 結果與討論
不同來流風向會在街谷建筑群周圍產生不同的氣流場,進而影響到污染物的擴散,因此對比分析兩種盛行風向(西北風、北風)的氣流速度分布和污染物擴散規律。
2.1 典型測試高度選擇
為獲取更清晰、有效的模擬效果,以北風為例,考察不同高度處污染物摩爾濃度和氣流速度分布,結果見圖2。在北風下,隨高度升高,污染物濃度逐漸降低,氣流速度持續上升,兩者呈現反相關。距地10.0 m以下為污染物高濃度聚集區域,1.6~20.0 m內污染物濃度變化梯度較大,20.0 m以上污染物濃度變化較小,最后趨于零。高度小于40.0 m的居住建筑和公共建筑占總建筑數量的50%以上,30.0 m高度處的污染物對街谷污染物分布很重要[16]。因此,重點對典型高度,即1.6 m(人體呼吸面)、10.0 m(中低層)、20.0 m(多層)、30.0 m(小高層)進行分析。
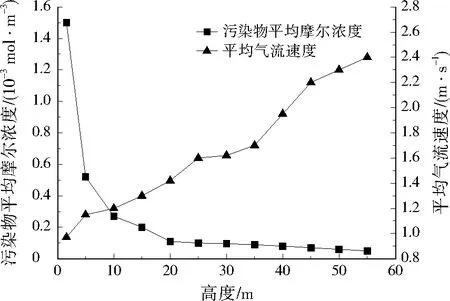
圖2 不同高度處污染物摩爾濃度和氣流速度分布
2.2 1.6 m高度處氣流速度和污染物濃度分布
如圖3所示,來流風向改變時,街谷內污染物濃度分布變化較大。在西北風下,每條街谷內污染物基本保持連續線狀分布。與北風工況相比,污染物在主干道B居中的位置大量聚集,并在臨近街谷中央偏西處形成帶狀濃度極大值區域。在支路A、C、D中,部分線狀污染物在街谷入口附近出現斷裂,且在街谷中分布不均勻,其中支路C下游區域污染物不斷聚集,此處不僅匯集了上游的污染物,還聚集了部分主干道西側的污染物。同時,部分污染物向建筑群中擴散,危及建筑群內居民的健康。與北風工況相比,圖4(a)中西北風時氣流受建筑阻擋,在街谷中發生多次繞流,氣流沿X軸45°方向進入街谷,在支路中的氣流繞流作用和北風工況相比差異極大,街谷越長,氣流在街谷中受建筑阻擋發生的繞流次數越多,進而影響街谷內污染物的擴散;主干道中氣流的繞流作用減弱。街谷內的平均氣流速度比北風工況小很多且較穩定,均不超過4.0 m/s,尤其在支路中A、C、D中極其明顯,未在街谷中形成類似于圖4(b)中的“狹管效應”,僅在主干道入口和出口處形成大片氣流速度極大值區域。
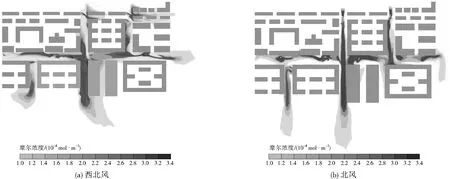
圖3 兩種風向距地1.6 m處污染物摩爾濃度分布
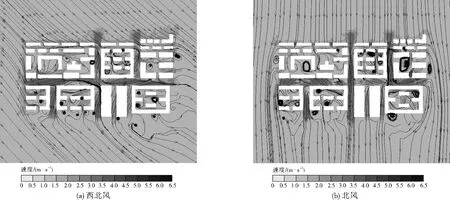
圖4 兩種風向距地1.6 m處氣流速度流線
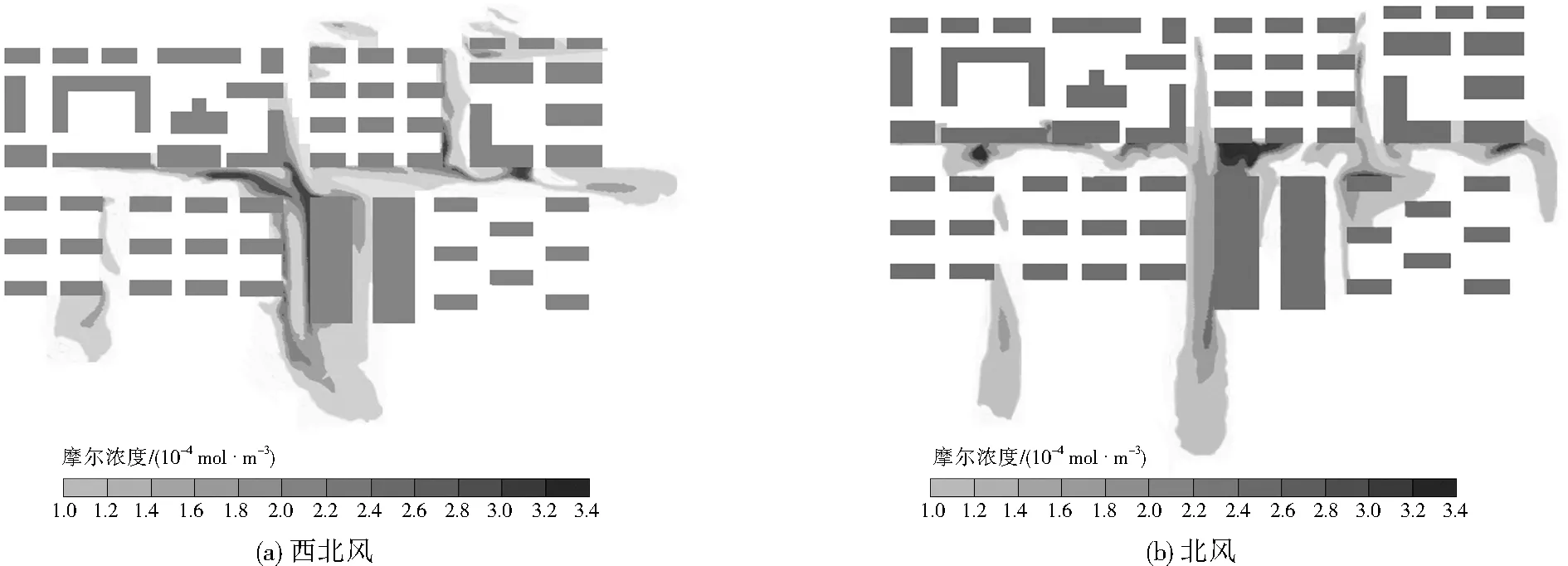
圖5 兩種風向下距地10.0 m處污染物摩爾濃度分布
2.3 10.0 m高度處氣流速度和污染物濃度分布
由圖5可見,與北風工況相比,西北風時街谷內污染物濃度分布變化較大,每條街谷內污染物基本保持線狀和部分團狀分布,受來流風的影響污染物整體向東側和南側擴散,且污染物也在主干道B居中的位置大量聚集,并在臨近街谷中央偏西處受交匯氣流的影響形成大片帶狀高濃度區域;在主干道B居中的兩側,污染物主要聚集在街谷背風面一側。由圖6可見,與北風工況相比,西北風向時支路中形成數片靜風區,且氣流速度遠小于主干道B。遠離建筑群東南向形成大面積低氣流速度靜風區,而在北風時,在遠離建筑群南向形成更大面積的靜風區。該高度處氣流流線部分與1.6 m高度處相似,街谷中氣流受建筑物的阻擋發生繞流作用極其明顯,北或西北側流入的氣流很大程度上影響到下游側流場的分布。
2.4 20.0 m高度處氣流速度和污染物濃度分布
由圖7可見,在20.0 m高度處矩形框位置不存在建筑,上游開敞空間增大,在此處西北風向氣流的灌入使街谷中的氣流發生了根本變化,導致街谷內污染物擴散趨勢也發生了很大變化。此時,矩形框西側的主干道內已無污染物,矩形框南側街道受兩側氣流的擠壓,在此處聚集了大量污染物,而在矩形框東側的主干道則分裂成多個團狀分布的污染物;支路僅在支路C、D處聚集了部分多塊斷裂團狀污染物。總之,東側建筑群處污染物濃度遠大于西側。在北風氣流的作用下,污染物在矩形框東南側街道呈條狀分布,在主干道B及建筑群南側以團狀聚集。由圖8和圖6相比,在該高度處上游氣流的繞流作用減弱,并在矩形框內形成氣流速度極大值區域,而在部分支路形成低氣流速度的靜風區。總之,由于西北風工況迎風面積大于北風工況的迎風面積,因此氣流的斜向吹入對此高度處污染物的擴散更有利。
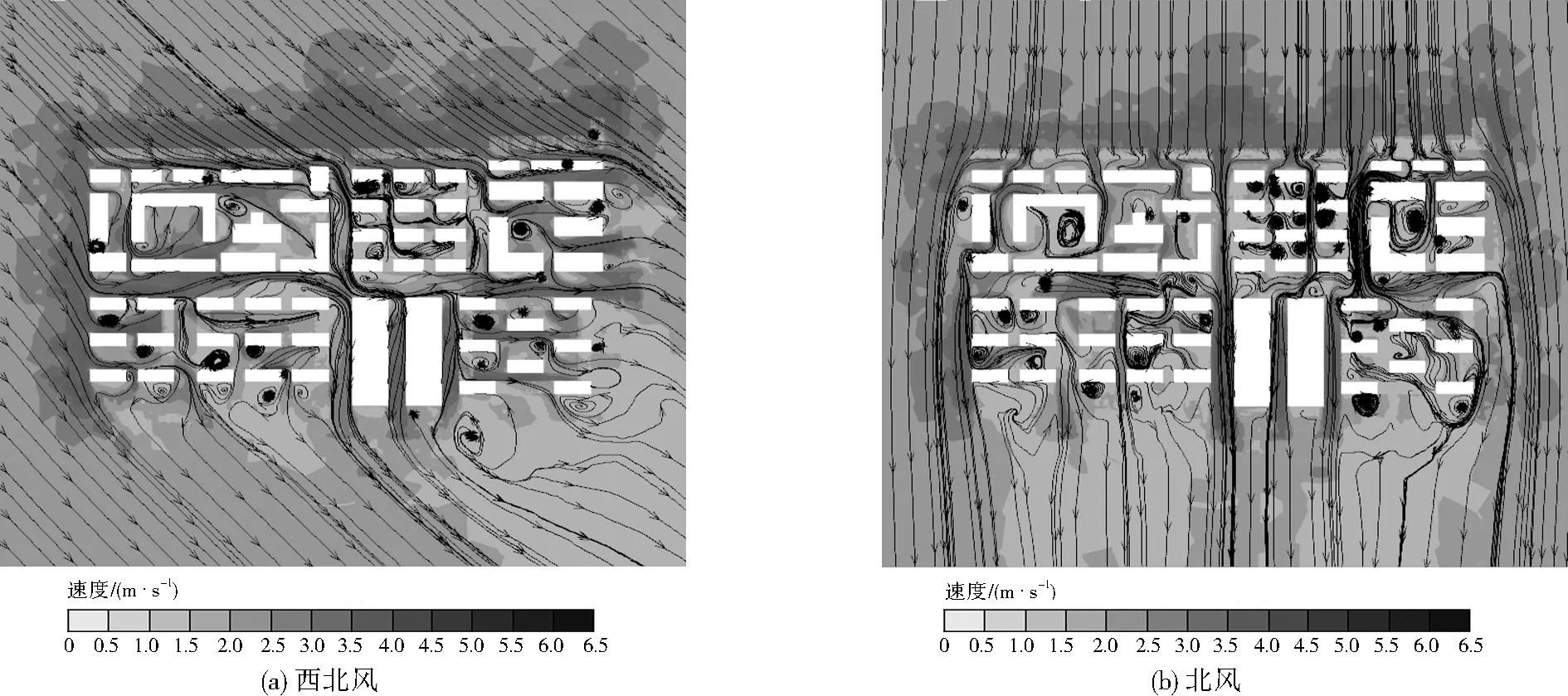
圖6 兩種風向距地10.0 m處氣流速度流線
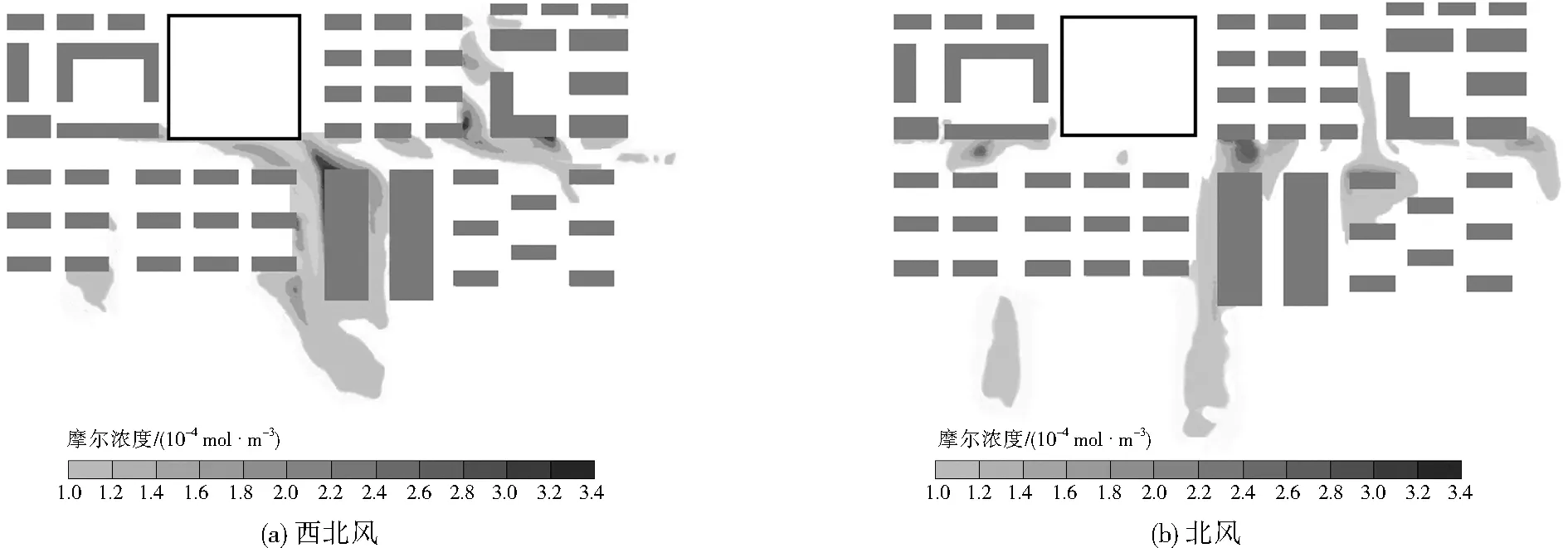
圖7 兩種風向下距地20.0 m處污染物摩爾濃度分布
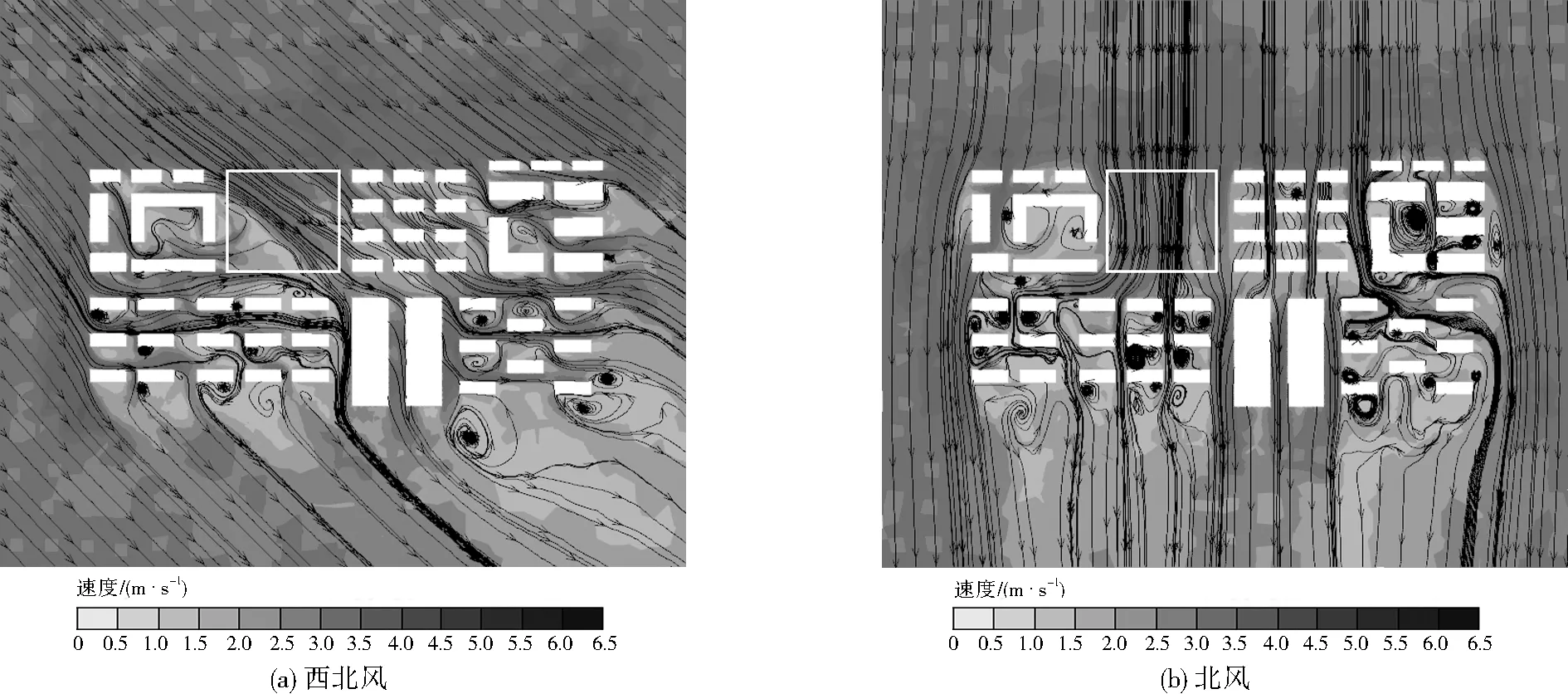
圖8 兩種風向距地20.0 m處氣流速度流線
2.5 30.0 m高度處氣流速度和污染物濃度分布
由圖9可見,30.0 m高度處建筑群密度降低,矩形框位置不存在建筑,西北風向時街谷西側基本無污染物,在主干道中僅在矩形框東側和居中位置存留部分團狀污染物,受風向的影響,在支路C、D處受建筑的阻礙作用停留一些污染物,并逐漸向下游擴散。北風向時,團狀污染物主要分布于主干道B中,較少污染物位于建筑群南側,繼續向下游擴散。由圖10和圖6、圖8相比,30.0 m高度處西北風向的氣流繞流作用減弱。西北側矩形框處流入的氣流將整個街谷分隔成兩段,從矩形框流入的大部分氣流向南側和東側擴散,而在西側流入街谷的氣流受矩形框處流入氣流的阻擋順著來流方向擴散出建筑群外,同時也在建筑群外的東南側形成大部分靜風區。由于建筑群對北風向的氣流速度造成的衰減,靜風區在建筑群南側形成。總的來說,通過控制建筑的連續界面誘導街谷中的氣流橫向繞流,或在臨街上游設置合適的開敞空間,以增加來流通風廊道,可有效改善街谷中污染物的擴散。
文獻[17]給出了城市街道峽谷中人員停留區內污染物停留時間(τ,s)的計算公式(見式(2)),對分析街道峽谷中污染物擴散有重要價值。其模型以三維城市典型街道峽谷建筑群為對象,與本研究的模型相似,因此同樣采用式(2)計算不同風向下街道人員停留區內污染物停留時間,結果如表1所示。兩種風向下每條街道人員停留區內污染物停留時間排序規律相同,都滿足街道C>街道A>街道B>街道D的規律;不同風向下每條街道人員停留區內污染物停留時間不同,說明風向對每條街道內污染物的影響存在差異,每段街谷內的污染物擴散分布不是孤立系統,而是相互關聯的有機整體,具體路段污染物的分布受臨街和上下游建筑密度等多重因素的影響,單一因素的改變會對臨近等多處位置造成影響。
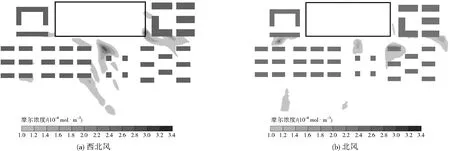
圖9 兩種風向下距地30.0 m處污染物摩爾濃度分布
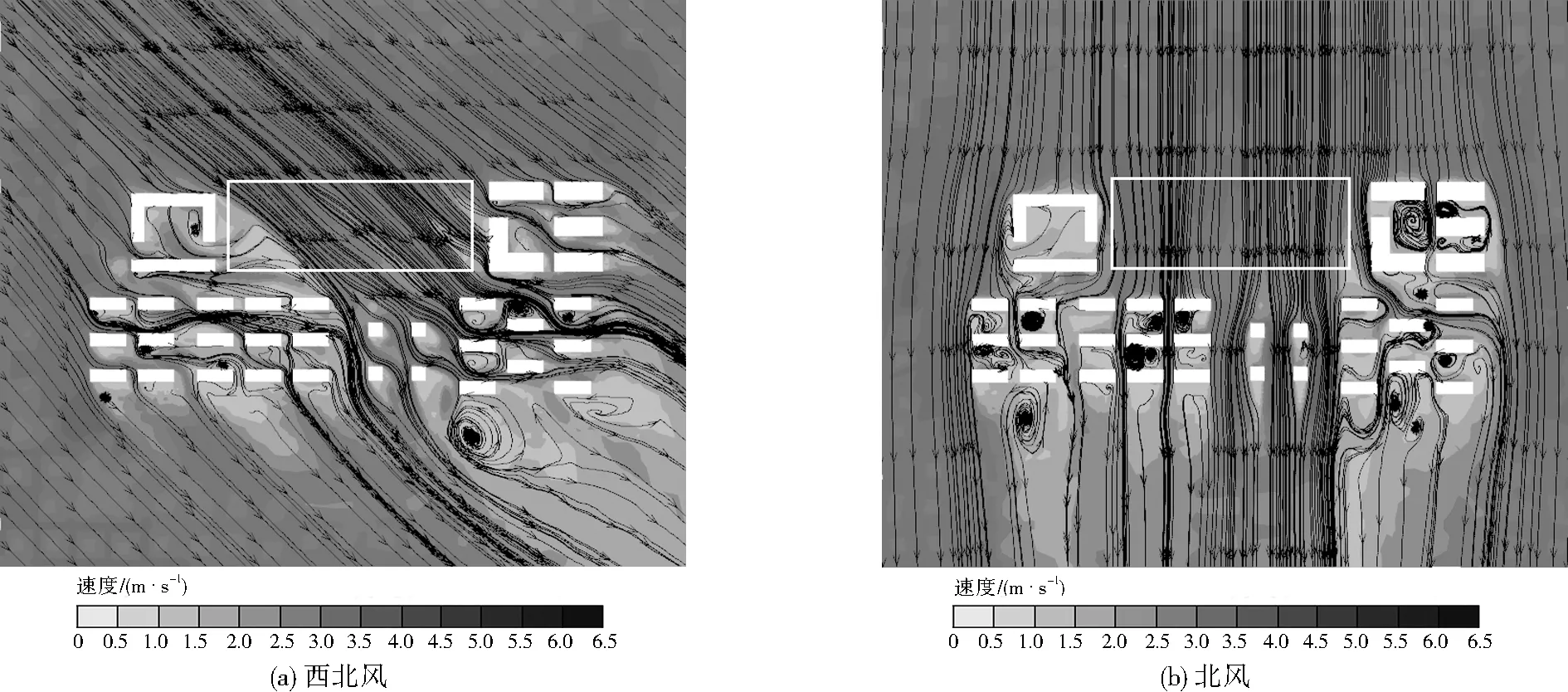
圖10 兩種風向距地30.0 m處氣流速度流線
(2)
式中:C為人員停留區污染物平均質量濃度,kg/m3;W為街道寬度,m;L為街道長度,m;h為人員停留區高度,m,取1.6 m;q為單位時間內污染物排放強度,kg/s。

表1 不同風向下街道人員停留區內污染物停留時間
3 結 論
(1)北風時,距地10.0 m以下范圍是污染物高濃度聚集區。與北風工況相比,西北風時街谷內污染物濃度分布變化較大,沿高度截面上升依次呈連續線狀→線狀和部分團狀→斷裂團狀。
(2)隨著建筑高度的增加,主干道中的氣流繞流作用減弱。通過控制建筑的連續界面誘導街谷中的氣流橫向繞流,或在臨街上游設置合適的開敞空間,以增加來流通風廊道,可有效改善街谷中污染物的擴散。
(3)兩種風向下每條街道人員停留區內污染物停留時間排序規律相同;不同風向下每條街道人員停留區內污染物停留時間不同,說明風向對每條街道內污染物的影響存在差異,每段街谷內的污染物擴散分布不是孤立系統,而是相互關聯的有機整體。

