基于動態規劃模型的救災物資路線規劃問題
(西南石油大學 四川 成都 610500)
引言
我國是自然災害頻發國之一,自然災害給我國帶來的損失巨大。由此,國家特別重視自然災害救助問題,在各地相繼建立救災物資儲備庫,救災物資儲備庫的物資由分布在全國各地的生產廠家提供。除了生產廠家捐贈的救災物資以外,另外的物資由國家救災指揮部統一購買,各個地區的民政部門負責本地區的物資集中和運送,并需要付出物資的購買費用以及運輸費用。
問題提出
10家產品生產廠家用Si(i=1,2,…,10)表示,能夠提供的物資有5種,分別是:M1,M2,M3,M4,M5,需要物資供應的18地區用Dj(j=1,2,...,18)表示。根據物資實際生產狀況要求,部分供應物資生產量有最低要求:如果訂單量低于此線,則不開工生產。由于部分物資的使用可以相互替代,對于需求地區Dj,如果要訂購的話,M1和M2僅需訂購一種,M3和M5僅需訂購一種,其它需求沒有特別的要求。根據各種物資的實際作用,對每個需求地區而言,有最低需求量和額外需求量。
節點之間(包括生產廠家、需求地區,以及道路的連接點)的道路里程如圖1所示,標注在圖中道路一側,每種物資單位里程平均運輸費用已知,產品的訂購價格按照一定的數量實施分段定價原則。通過建立數學模型,來確定生產訂單以及物資運送路線,希望以最小的費用代價,完成救災物資的訂購和運輸要求。
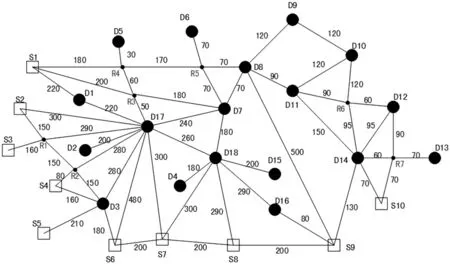
圖1 地區分布圖
問題分析
為了得到以最小費用為代價的生產訂單與物資運送路線組合[1],需要知道各個地區的所需物資組合。但由于各種約束條件,該組合是動態變化的,可以分兩個階段來考慮。
階段一:最簡單的模型是找到生產廠家到地區之間單位數量物資所花費用最低的路徑。
階段二:在階段一的前提下,繼續滿足各廠家Si供給各地區Dj物資Mk的數量的各項約束條件,即為各個廠家供應能力、廠家物資生產的最低數量要求、各個地區的額外物資需求、最低需求量和部分物資的使用可以相互替代等約束條件,那么一定會在階段一中的路徑中找到一簇符合最優總費用的最優路徑,即可確定生產訂單。
動態規劃模型的建立
第一階段 最短路模型[2]的建立
由問題分析可知,物資的總費用P包括購買費用Pmj以及運輸費用Ptj,讓總費用達到最小化,核心的問題是廠家Si(i=1,2,…,10)到需要物資供應的地區Dj(j=1,2,...,18)的路程最優。
對于題中的距離問題,將18個需要物資供應的地區Dj、10家生產廠家Si以及道路的連接點Ru看做由35個點連接成的網絡圖(其中,生產廠家Si為1~18,道路的連接點Ru為11~17,地區Dj為18~35),構造賦權圖[3]G(V,E,W),如圖2所示。其中,頂點集V={v1,…,vn},其中v1,…,vn表示35個頂點,E為邊的集合;鄰接矩陣W=(wxy)n×n,wxy表示頂點vx和vy之間的距離,若兩點之間無道路相通,則wxy=∞,問題便是求賦權圖G中兩頂點所具有最小權的路。
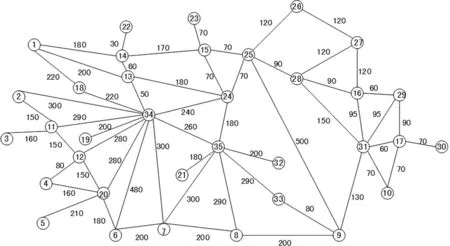
圖2 物資運輸問題的無向賦權圖
取點i到點j的路程dij作為邊(vi,vj)的權wij,即
假設先不考慮廠家的供應能力、廠家物資生產的最低數量要求以及各個地區的額外物資需求等約束條件,使得地區Dj到距自己最短路程的生產廠家處就能滿足自己所需物資的最低需求,通過賦權圖計算兩點之間的最短距離。
目標函數 若設決策變量xij=1表示邊所選擇的路線均為各單位之間的最短距離,此時的權重為dij。則地區Dj到廠家Si的距離dij的最短路模型為:
若設單位物資所花費用為pij,此時的最優路徑距離為sij。我們將定義目標函數每段路線上的權重wij=pijsij,則目標函數變為:
求得的結果為生產廠家到地區之間單位數量物資所花費用最低的路徑。
第二階段 在第一階段的基礎上,繼續滿足各個廠家供應能力、廠家物資生產的最低數量要求以及各個地區的額外物資需求等約束條件,此時將在階段一的結果——生產廠家到地區之間所花費用最低的路徑中找到滿足約束條件的總費用的最優路徑。
約束條件
xijk為廠家Si供給地區Dj物資Mk的數量,xijk≥0。則:
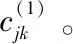
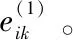
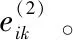
(6)
最后,由于部分物資的使用可以相互替代,M1和M2僅需訂購一種,M3和M5僅需訂購一種。因此:
目標函數 設任意生產廠家到任意地區之間所花費用最低的最優路徑的每單位物資Mk共花費用為Wijk元。則可得到生產廠家到地區之間所花費用最低的路徑中找到滿足約束條件的總費用的目標函數為:
生產訂單數Xik目標函數為:
綜上,整合為:
模型求解 此模型的求解采用Floyd(弗洛伊德)算法[4],它是一種矩陣(表格)迭代方法,該算法是通過對表示有向圖的鄰接矩陣作迭代計算,來解決有向圖任意一對頂點之間的最短路徑問題。
Step1:整合所有數據,求得任意兩點的距離矩陣。
Step2:結合Floyd算法,求出關于單位物資所花費用為pij的任意兩點的鄰接矩陣,該鄰接矩陣即為任意兩點的最優路徑。
Step3:在Step2所得路徑下,帶入廠家Si供給地區Dj物資Mk的數量xijk,使用目標費用函數求得總費用。
Step4:將上步中得到的總費用進行比較,得到最小總費用。
Step5:根據廠家Si供給地區Dj物資Mk的數量xijk確定生產訂單。
模型總結
本文采用的動態規劃模型能夠得到題中所需的一簇最優解,動態規劃方法反映了動態過程演變的聯系和特征,在計算時可以利用實際知識和經驗提高求解效率。本文的最短路模型采用Floyd算法,其算法可以求解任意兩點之間的距離,應用范圍比Dijkstra算法要廣。模型的劣勢表現在文中的動態規劃模型沒有統一的標準模型,在數值方法求解時存在維數災,采用最短路模型的Floyd算法,其時間復雜度比較高,并且在對數據的整合分析過程中,不考慮額外需求量對最低費用的影響,會對結果產生相應的誤差。在第二階段中,將各個影響總費用的因素采取先分后合的方法,對于因素的影響具有一定的主觀因素。

