基于移相技術的改進等精度測頻法

李海生

（長治學院電子信息與物理系，山西長治 046011）

頻率作為脈沖信號的關鍵參數，在很多時候需要測量其精確值。如在航空領域，諧振式壓力傳感器常用來測量飛行器高度和空速，其輸出的信號就是頻率信號，獲取實時準確壓力值的關鍵就在于頻率測量的響應速度和準確性[1-2]。在地質勘探和醫療檢查等領域廣泛使用的磁探測技術中，光泵磁力儀作為磁梯度探測的常用探頭，其信號輸出也是方波，其頻率值與磁場值成比例，磁場的測量精度也取決于頻率的測量[3-4]。隨著電子技術和集成電路工藝的發展，信號頻率不斷提高，傳統的頻率測量方法已經滿足不了越來越高的測量精度要求[5]。本文通過對傳統頻率測量方法的分析比較，結合最新的技術發展，提出了一種基于等精度頻率測量的改進型方法，可以使得基于現有的硬件運行最高速度上再提升幾倍測量精度。

1 頻率測量方法

在現代測頻技術中，頻率測量一般采用電子計數法較多，通過電子計數器對周期信號在單位時間內變化次數的計數，從而得到其頻率值。測量頻率一般常用的三種方法，分別是測頻法、測周法和等精度測頻法[6]。

1.1 測頻法

測頻法是通過在一定閘門時間T0內對被測信號進行頻率計數，通過得到的計數值Nf來計算被測信號的頻率fx，其計算方法：

當T0取1s 時，計數值Nf就是被測信號的頻率。但由于閘門時間T0無法與被測信號同步對齊，可能存在±1的計數誤差，這種頻率量化到來的誤差又稱為量化誤差，用相對誤差表示為：

這種測量方法的精度主要取決于計數誤差，當T0一定時，由式（2）可知，相對誤差與被測信號的頻率fx反比，當測量的信號越大時，測量的相對誤差就越小，所以測頻法適用于高頻信號的測量[7]。

1.2 測周法

測周法也叫周期測頻法，是將被測信號的周期作為計數的閘門時間，對標準信號fs的脈沖計數來得到測量信號的周期。當閘門寬度是被測信號的一個周期Tx時，通過計數的結果Nt就可以計算出被測信號頻率fx，即

測周法有類似于測頻法的±1的計數誤差，表示為：

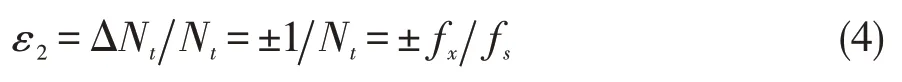
由式（4）可知，當標準信號周期fs一定時，測周法的相對誤差是隨著測量頻率的減小而減小，故此方法適合測量低頻信號[7]。

1.3 等精度測頻法

等精度測頻法是測頻法的延伸和改進，是利用閘門時間對被測信號和標準信號同時進行脈沖計數，不過這個閘門時間是不確定的值，而始終保持為被測信號周期的整數倍[8]。

在等精度測頻中，通過閘門信號來控制兩個計數器分別對被測信號為fx和標準時鐘信號fs進行計數，得到計數結果分別為Nx和Ns。那么被測信號頻率為：

在測量過程中，預置閘門信號開啟時（即預置閘門上升沿到來），兩個計數器并不馬上開始進行計數，而是等被測信號fx的上升沿到來時，計數器才真正開始工作[9]。同樣，在預置閘門信號關閉時，計數器也不立即停止工作，而是等被測信號fx的最近一個上升沿到來時才結束計數，完成一次測量，測量的時序關系如圖1所示。

圖1 等精度測頻時序圖

由圖1可以看到，實際閘門信號時間τ并不一定是預置閘門時間τ0，而是根據被測信號fx微調整過的，前提是保證每次閘門信號有效時間是被測信號周期的整數倍，即：

因此，這種方法有效的避免了對被測信號計數Nx所產生的±1的計數誤差，不會出現類似于測頻法的低頻精度差，高頻精度高的現象。在忽略標準信號fs本身誤差（晶振等產生的誤差），此時精度測頻法的誤差主要來源于對標準時鐘信號計數Ns的±1誤差[10]，相對誤差為：

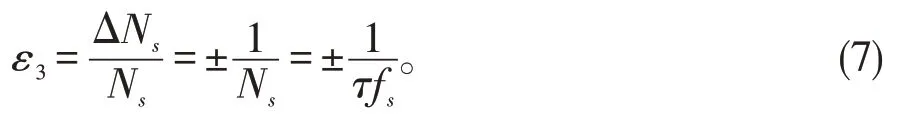
通過式（7）可知，測量頻率的相對誤差與被測信號頻率無關，僅與實際閘門時間τ和標準時鐘信號fs有關，所以說是等精度測頻法的測量精度在整個測試頻段內都是一樣的，不會隨測量頻率而改變。

2 基于移相技術的等精度測頻法原理

等精度測頻法作為常用的一種頻率測量方法，其測量精度不受測量信號頻率的影響，只和計數的閘門時間和標準時鐘頻率有關。由于延長計數閘門時間會影響到測量的實時性，所以只能通過提高標準時鐘信號的頻率來提高測量精度。盡管利用FPGA 里的倍頻技術可以將晶振時鐘提高到幾百兆，但由于FPGA 最高工作頻率的限制，達到硬件的極限后無法繼續再提高。

通過采用移相技術，使用多路移相的同頻時鐘，同時進行頻率測量計數，這種改進型方法可以在等精度測量的基礎上進一步提高測量精度。其原理是將標準時鐘信號fx進行移相產生多路時鐘信號，在閘門時間內，多路時鐘信號同時進行計數，由于幾路時鐘信號有相位差，可以減小Ns的±1計數誤差，從而將測量精度提高幾倍[11-12]，基于4路移相時鐘的等精度測頻時序如圖2所示。

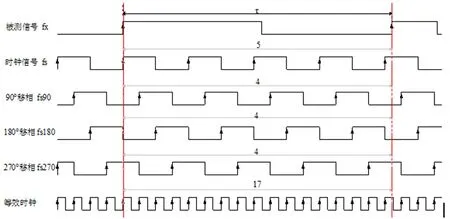
圖2 基于4路移相時鐘的等精度測頻時序圖

在圖2 中，4 路標準時鐘信號fs，fs90，fs180，fs270是同頻時鐘，相位分別是0°，90°，180°，270°，這4路時鐘在閘門時間τ內同時進行計數，計數值分別為5，4，4，4，其和為17，通過除以時鐘數得到較為精確的計數值為4.25，與一路時鐘相比，精度提高了4倍。如果同頻時鐘增加到m路的話，其每路時鐘相移為2π/m，第k路時鐘的計數結果為Nk，則最后頻率測量計數結果為；

將式（8）代入到式（7）可得，改進的等精度測頻法的相對誤差為；

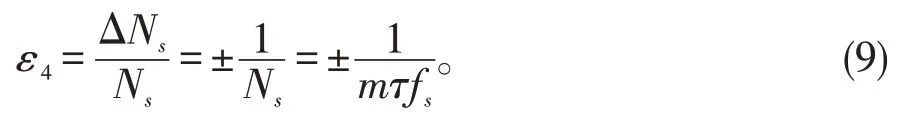
采用m路不同相位的時鐘信號進行等精度測頻，其測量精度相比于傳統的一路時鐘測量，可以提高m倍。

3 測頻系統的設計驗證

通過采用FPGA 和單片機相結合，設計了頻率測量系統，對改進型的等精度頻率測量方法進行實驗驗證。FPGA 選用Altera 公司低成本、低功耗的Cyclone IV 系列芯片EP4CE15E22C8N，單片機選用32位的處理器STM32F103RCT6。先通過FPGA完成外部脈沖信號的頻率計數，再將得到的頻率數據通過RS232整體打包發送給單片機進行數據處理和參數信息顯示，頻率測量系統設計框圖如圖3所示。

圖3 頻率測量系統框圖

采用時鐘倍頻技術和時鐘移相技術相結合，在FPGA對改進的等精度測頻法進行了驗證。由外部晶振給FPGA 提供50 MHz 的時鐘輸入，經FPGA 內部的PLL 倍頻和移相，產生4 路相位分別為0°，90°，180°，270°的250MHz 標準同頻時鐘信號clk_250M_0，clk_250M_90，clk_250M_180，clk_250M_270。通過閘門信號T0_gate 控制被測信號計數器fx_cnt 和4 個不同相位的時鐘信號計數器fbase0_cnt，fbase90_cnt，fbase180_cnt，fbase270_cnt的工作，從而完成頻率測量計數，在ModelSim的仿真時序圖如圖4所示。

圖4 基于改進的等精度測頻法的仿真時序圖

當FPGA 監測到單片機發送的開始工作信號Start_sig后，FPGA就開始進行一次頻率的測量，并根據被測信號fx對預置閘門信號T0_gate進行調整，確保調整后的實際閘門信號Real_gate的有效時間τ是被測信號周期的整數倍。在閘門時間內，被測信號計數器和4 個標準時鐘計數器完成頻率的計數。當閘門信號結束后，計數器都停止工作，輸出計數值，FPGA 發送測量完成信號Done_sig 給單片機，并把數據通過串口發送給單片機，單片機完成數據的處理和信息顯示，至此測量系統完成一次頻率測量，接著FPGA等待下一次的開始測量信號。

在圖4 的仿真時序圖中，輸入信號fx的周期是30.6 ns，4路標準時鐘信號周期是4 ns，為了仿真方便，預置閘門時間τ設置為100 ns，而實際閘門信號是Real_gate，根據仿真結果可以看到，有效時間調整成了3倍的被測信號周期。Nx的計數值3，4路標準時鐘信號計數值分別為22，23，23，23，通過式（8）計算可得得到計數結果Ns是22.75，代入到式（5）可得被測信號的周期約是30.33 ns。由式（9）可知理論的相對誤差為1%，實際測量的相對誤差為0.87%，相比于一路時鐘進行等精度測量，測量的精度提高了4倍。

預置閘門有效時間τ取1 μ s 時，改進的等精度測量系統相對誤差可達0.1%.。τ的取值會影響到測量的相對誤差，一般τ至少是大于被測信號的一個周期。當τ太小會在測量低頻信號時，測量的相對誤差會比較大。太大會影響到頻率測量的動態響應，導致測量周期變長，無法實時反映出頻率的變化，所以，一般根據實際應用場景擇中選擇。

4 結語

通過利用鎖相環的倍頻和移相技術，對傳統的等精度測頻法進行了改進，采用多路移相的同頻時鐘同時完成測頻計數，相比于原有的測量精度可以提高多倍，在器件工作最高頻率的限制的基礎上提高測量精度。最后使用FPGA和單片機設計了頻率測量系統，通過在FPGA 上進行實驗驗證，設計的基于4路移相的同頻時鐘測量系統，其測量精度相比于傳統的等精度測量提高了4倍。此方法可以應用于動態的高頻信號的實時頻率測量中，同時，還可以用來精密時間間隔的測量，比如脈沖的上升沿和下降沿等，具有很廣泛的應用價值。