MATLAB仿真技術在電路暫態分析中的應用

李 強

（運城學院機電工程系，山西運城 044000）

直流電路的暫態分析是“電工技術”的重要內容，是機電類專業學生需要掌握的重點知識。由于該類電路含有儲能元件，在分析過程中涉及到常微分方程的求解過程，使得學生對電路分析感到困難。因此，針對教學內容，利用現代電子仿真技術探索新的教學方法和手段勢在必行[1]。

MATLAB是MathWorks開發的科學與工程計算軟件，它以矩陣運算和符號運算為基礎，內含豐富的算法，把繪圖及動態系統系統仿真等功能有機融合在一起[2]。目前已有學者對進行了MATLAB在暫態電路中的應用研究。主要是進行二階電路的頻率特性研究以及響應的Simulink仿真，但不適合非電類專業學生學習。還有學者進對一階RC的電路進行Simulink仿真并繪制出電路的響應曲線，而對一階RL電路的暫態研究較少。

本文在上述文獻的基礎上，以直流電機的勵磁繞組為例，研究感性負載在直流電路中的響應過程。首先在對電路進行建模的基礎上，利用符號常微分方程求解的方法，來求解系統的一階零狀態響應和零輸入響應。最后給出了一階RL電路模型對應的響應曲線，在此基礎上，對系統的參數進行分析。

1 一階RL系統模型

直流電機中，勵磁繞組通以直流電來建立主磁場，工作時它分為建立磁場和關閉磁場兩個階段[3]。圖1 為一個參數為L、R 的電機勵磁繞組。整個電路由電源Us、開關K、電阻R、R1和電感L組成，將流過電感的電流iL及電感兩端的電壓UL作為電路的輸出。

建立磁場電路模型，流過電感電流由零變為穩定值。該過程包括開關K斷開時的初始穩定狀態1(t＜0)，開關K接至位置1后的暫態過程(t≥0)以及新的穩定狀態1。等效電路如圖2所示。分析如下：

初始穩定狀態1 為iL=0；新的穩定狀態1 為

由于初始穩定狀態1電感無儲能，電路處于零狀態。根據基爾霍夫電壓定律和電感元件的時域伏安特性可得方程組(1)。

求解微分方程iL1、uL1便可求出開關K 接至位置1后的零狀態響應。

關閉磁場電路模型，流過電感電流由穩定值變為零。該過程包括開關K接至1時初始穩定狀態2，開關K 接至位置2 的暫態過程(t≥0)以及新的穩定狀態2。等效電路如圖3所示。電阻R1是為了加快繞組中電流的下降過程而設置的耗能電阻[4]。分析如下：

由于換路后電路無輸入激勵，電路處于零輸入。此時電路響應特性通過方程組2來描述。

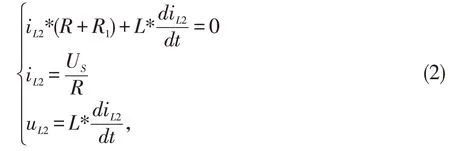
求解微分方程iL2、uL2便可求出開關K 接至位置2后的零輸入響應。

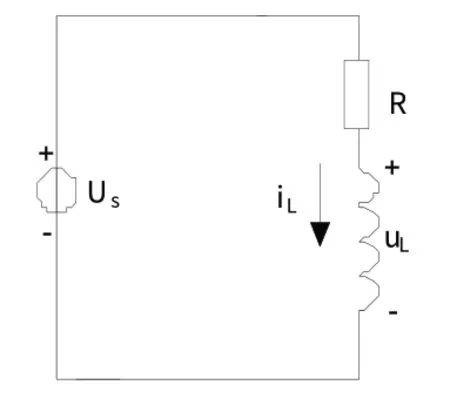
圖2 建立磁場電路模型

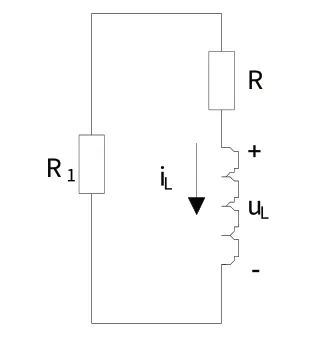
圖3 關閉磁場電路模型

2 系統模型的仿真與實現

2.1 符號常微分方程的求解

MATLAB內部集成符號運算工具箱，提供符號運算功能。應用符號計算，可以直接對抽象的符號對象進行各種計算，并獲得問題的解析結果。desolve函數實現以符號方式對常微分方程進行求解，得出其解析解[5]。

零狀態響應對應的方程組1的求解語句如下：

整理后即可得到電路2中電感元件的零狀態響應方程組（3）如下：

零輸入響應對應的方程組2的求解語句如下：

代碼運行結果為：

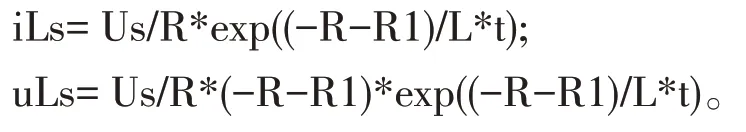
整理后即可得到電路3中電感元件的零輸入響應方程組（4）如下：

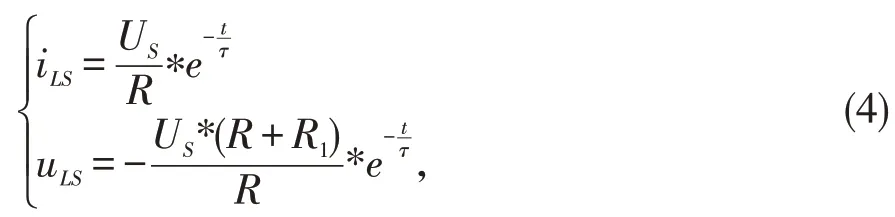
某臺直流電機的勵磁繞組參數如下：US=40 V,L=1 H,R=5 Ω,R1=10 Ω 。將其帶入方程組3 可得此臺直流電機繞組的零狀態響應，計算結果為方程組5所示。將其帶入方程組4可得它的零輸入響應，計算結構為方程6所示。

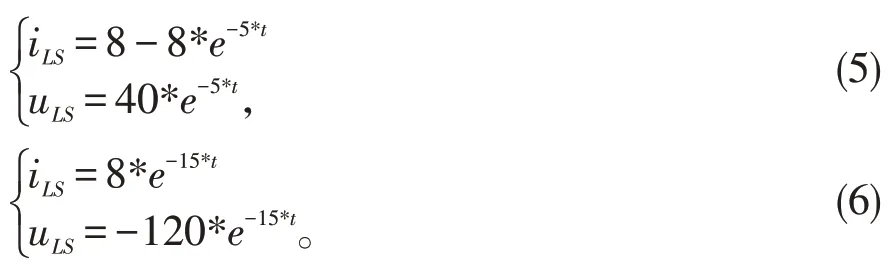
2.2 暫態曲線繪制

采用MATLAB中提供的二維繪圖函數plot來繪制電路2與電路3的暫態變化過程。

基于公式5 來繪制圖2 對應的零狀態響應圖形。時間區間為[0,2]，步長為0.01 s，程序段1為電感電流的響應過程，程序段2 為電感電壓的響應過程。

程序段1：

程序段2：

繪圖結果如圖4 所示。圖中uLs 線條表示電路零狀態響應過程中，勵磁繞組電壓的變化情況；線條iLs 表示該過程時勵磁繞組電流變化情況。

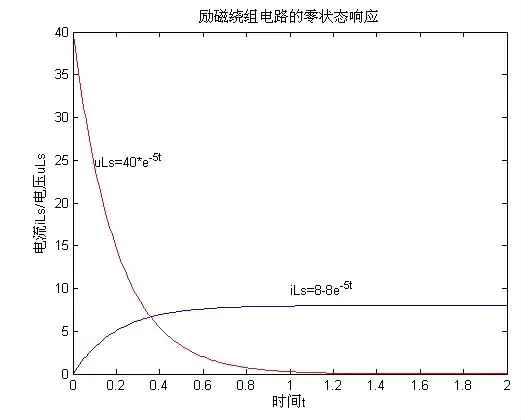
圖4 零狀態響應曲線

基于公式6 來繪制圖3 對應的零輸入響應圖形。程序段3 為電感電流的響應過程，程序段4 為電感電壓的響應過程。

程序段3：

程序段4：

繪圖結果如圖5 所示。圖中線條uLs 表示電路在零輸入響應過程中，勵磁繞組電壓的變化情況；線條iLs 表示該過程時勵磁繞組電流變化情況。

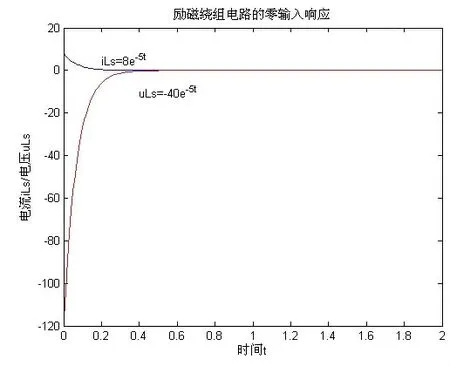
圖5 零輸入響應曲線

3 系統仿真結果分析

由圖4 可知，對于零狀態響應而言，流過電感的電流不會發生突變，電流方向與電感兩端的電壓方向一致，電感電壓由最初的40 V 衰減為0 V。最終電路達到新的穩定狀態，此時uL=0 V，iL=8 A。由圖5 可知，對于零輸入響應而言，流過電感的電流也不會突變，其電流大小從8 A減小為0 A，電感兩端的電壓方向與電流方向相反，其電壓從-40 V衰減為為0 V。最終電路達到新的穩定狀態。此時，uL=0 V,iL=0 A。在電路的兩種響應圖中，儲能元件電感兩端的電壓和流過它的電流，總是以指數形式變化。

時間常數τ對電路暫態過程的影響。如圖6所示，當耗能電阻為R1=10 Ω 時，該電路的時間常數為≈0.067，此時電感元件響應過程為曲線uL(10),iL(10)；當耗能電阻為R1=0 Ω 時，該電路的時間常數為=0.2，電感元件響應過程為曲線uL(0),iL(0)。由圖可知，R1越大，時間常數越小，電感元件越容易釋放能量，暫態過程越短，但對電感元件的耐壓有更高的要求。相反，時間常數大，電感不容易釋放能量，暫態過程較長。

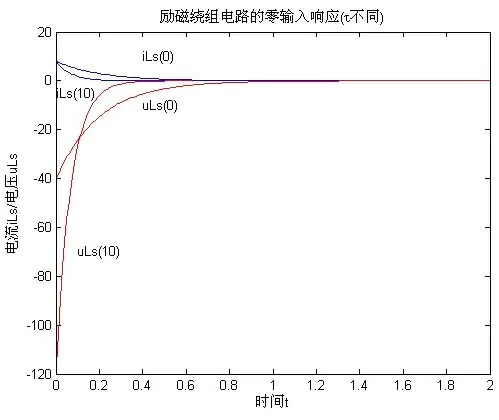
圖6 時間常數τ 對電路暫態過程的影響

4 結語

本文以給定參數的直流電機勵磁繞組為例，分析了其建立磁場和關閉磁場的兩種電路模型，通過MATLAB 軟件計算出該電路下的零狀態響應和零輸入響應，并以圖形的形式反映響應結果，從而得出一階RL 電路中的電感元件的電流變化規律以及時間常數對電路暫態過程的影響。

在直流暫態電路教學中引入MATLAB 虛擬仿真軟件，利用其強大的運算和可視化功能，通過現場簡單編程計算、曲線繪制，使原本抽象的內容變得生動，復雜的數學計算變得容易，這將增強學生對RL 一階電路工作過程的理解，激發學生對自然科學工程技術的好奇心和學習興趣。