基于ARMA-GARCH模型的南寧市O3濃度預測研究*

梁 煒，李雅箐，黃喜壽，李宏姣

(1.廣西壯族自治區環境信息中心，廣西南寧 530028；2.廣西壯族自治區環境保護科學研究院，廣西南寧 530022)

0 引言

城市中近地面的臭氧是由人類活動排放的NOx、CO 和VOCs 等前體物在特定大氣環境條件下發生復雜的化學反應生成的二次污染物[1]。近年來隨著城市機動車保有量的激增，南寧近地面空氣中O3污染問題日益嚴重，已成為南寧市大氣污染防治重點工作之一。如何準確預報近地面臭氧濃度成為當前一個熱門研究課題。

目前大氣污染物濃度預測主要分為數值預測[2-3]和統計預測[4-8]兩種方法。由于氣象條件的復雜性，以大氣動力學理論為基礎的數值模式污染物濃度預測方法需要消耗大量的計算時間。而基于統計模型的預測方法通常采用真實監測值，利用統計方法，建立預測模型，具有計算速度快的特點。時間序列模型作為統計預測法之一，已被廣泛用于大氣污染物濃度預測[9]，但主要還是集中在PM10、NOx等污染物的預測[10-13]上，用于O3濃度預測仍比較少。

本文通過構建ARMA-GARCH模型，對南寧市城區O3濃度進行預測，并對預測模型進行誤差評價，期望為大氣污染防治和預警預報提供支持。

1 材料與方法

1.1 數據來源

本研究以南寧市2017年1月1日-2017年12月31日日均O3濃度監測值為樣本，數據來源于廣西壯族自治區環境保護廳、廣西壯族自治區環境監測中心站按照《環境空氣質量指數(AQI)技術規定(試行)》的有關要求，實時發布的南寧市市區環境空氣自動監測站點，數據真實可靠。本研究使用EViews軟件對樣本擬合模型，預測2018年1月1日至2018年1月31日O3日均濃度，并對預測結果進行誤差分析和模型評價。

1.2 ARMA-GARCH建模基本原理

1.2.1 ARMA模型

時間序列是變量按時間間隔的順序形成的隨機變量序列，時間序列分析通常不需要建立在專業理論所體現的相互關系基礎之上，而是“讓數據自己說話”。本研究選用移動平均自回歸模型即ARMA模型。ARMA模型是描述平穩時間序列最常用的分析模型，由統計學家Box G.E.P.和Jenkins G.M.于20世紀70年代創立，用此模型對時間序列進行預測分析稱為博克斯-詹金斯(B-J)方法。其基本思想是構成時序的單個序列值雖然具有不確定性，但整個序列的變化具有一定的規律性，可以運用時間序列的過去值、當期值及滯后擾動項的加權和建立模型來“解釋”時間序列的變化規律[14]。

ARMA(p，q)模型的一般形式為

xt=C+α1xt-1+…+αpxt-p-θ1μt-1-…-θqμt-q+μt，

其中參數C為常數，α是自回歸模型系數，θ是移動平均模型系數，μt是滿足獨立同分布的隨機誤差項(擾動項)。當 C=0，該模型成為中心化ARMA(p，q)模型；當q=0時，上式變為p階自回歸模型，記為AR(p)；當p=0時，上式稱為q階移動平均模型，記為MA(q)。

ARMA模型建立過程如圖1所示，主要由以下5個部分構成：

(1)數據預處理。通過時序圖初步判斷數據是否具有周期性、趨勢性、隨機性等特點。若存在相應特點，則對原始數據進行差分、對數變換等處理。

(2)平穩性檢驗。時間序列可以分為平穩序列和非平穩序列兩大類。時間序列數據的平穩有以下要求：均值、方差不隨時間變化；自相關系數只與時間間隔有關，而與所處時間無關。如果用傳統方法對彼此不相關聯的非平穩變量進行回歸，t檢驗值和F檢驗值往往傾向于顯著，從而得出“變量相依”的“偽回歸結果”，因此，在利用回歸分析方法討論變量有意義的關系之前，必須對變量時間序列的平穩性與非平穩性進行判斷[15]。

圖1 ARMA模型建模流程圖

(3)模型識別。通過樣本自相關函數分析(ACF)或樣本偏自相關函數分析(PACF)對模型滯后階數進行初步判定，之后再通過最小信息準則判斷赤池信息量準則(Akaike Information Criterion，AIC)值、施瓦茨信息準則(Schwarz Information Criterion，SIC)值和漢南-奎因準則(Hannan-quinn Criterion，HQ)值，選出最優階數。

(4)模型檢驗。通過白噪聲檢驗、殘差自相關性檢驗、異方差檢驗、系數顯著性檢驗，驗證模型的有效性。

(5)模型應用。對未來一段時間的O3濃度進行預測。

1.2.2 GARCH模型

yt=xtπ+εt。

GARCH模型的建立步驟：

(1)檢驗ARCH效應。在建立ARMA模型后，使用拉格朗日乘數法(LM法)或殘差平方自相關函數分析圖檢驗其是否存在ARCH效應，若存在ARCH效應則進入下一步。

(2)識別滯后階數，選取最優模型。通過對比各模型系數的顯著性與AIC、SIC、HQ值確定滯后階數后，選取最合適的模型進行建模。

(3)復驗ARCH效應。建立模型后仍然使用LM法或殘差平方自相關函數分析圖檢驗其是否仍存在ARCH效應，若仍存在ARCH效應，則返回上一步調整模型階數。

2 結果與分析

2.1 ARMA建模研究

2.1.1 數據預處理

使用Eviews軟件對南寧市2017年1月1日至2017年12月31日日均O3濃度監測值樣本數據進行模型參數估計，并根據監測值樣本數據構建時序圖，從圖2可初步判斷O3序列非線性近似平穩，因此無法確定其有周期性、趨勢性。為確定該序列的平穩性，對其進行平穩性檢驗并使用Augmented Dickey-Fuller (ADF)單位根檢驗方法判斷。

圖2 2017年O3日均濃度時序圖

Fig.2 Sequence diagram of average daily concentration of O3in 2017

檢驗結果表明(表1和表2)，ADF的t統計量(-8.244 276)小于1%顯著水平下的臨界值(-3.983 471)，可認為O3樣本序列在1%的顯著水平下屬于不含單位根的平穩過程，趨勢項(TREND)系數的P值大于0.05，可認為趨勢項系數顯著為零。常數項C系數P值小于0.05，表示常數項顯著不為零。即該O3樣本序列為帶有常數項、不含趨勢項、滯后階數為0的平穩序列。

2.1.2 模型識別

證明O3序列平穩之后，通過自相關函數分析初步為ARMA模型定階(表3)。

表1 O3平穩性檢驗與ADF單位根檢驗結果

Table 1 Results of O3stationarity test and ADF unit root test

t統計量tstatisticP值Prob.1%顯著水平下檢驗關鍵值Test critical values at 1% level5%顯著水平下檢驗關鍵值Test critical values at 5% level10%顯著水平下檢驗關鍵值Test critical values at 10% level-8.244 2760-3.983 471-3.422 218-3.133 955

表2 ADF檢驗方程

Table 2 Augmented Dickey-Fuller test equation

變量Variable系數Coefficient標準差Standard errort統計值tstatisticP值Prob.O3(-1)-0.316 0020.038 330-8.244 2760.000 0常數項C0.014 5930.002 2356.530 0660.000 0趨勢項(TREND)0.000 000 4250.000 006 590.064 4340.948 7

表3 O3自相關函數分析

Table 3 Analysis diagram of O3autocorrelation function

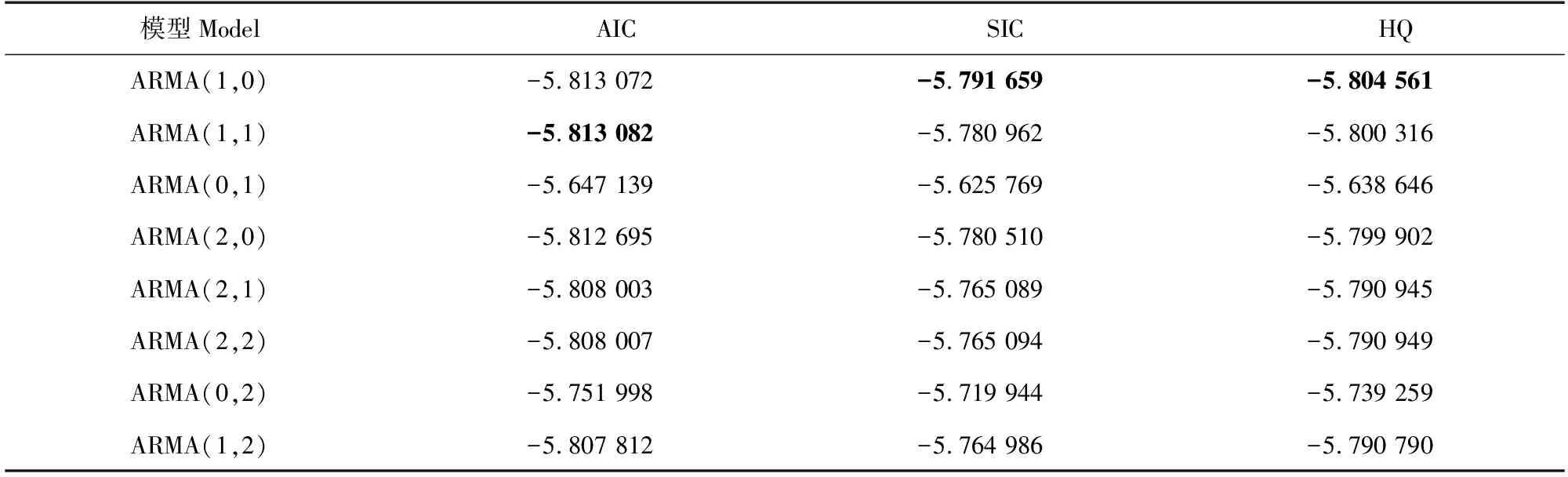
觀察表3發現自相關函數分析圖拖尾，偏自相關圖一階截尾，因此初步判斷模型形式為ARMA(1,0)。為確定模型形式與階數，同時采用AIC、SIC和HQ方法，使用最小信息準則判斷最佳階數。從表4可見，模型ARMA(1,0)在SIC和HQ中信息最小，在AIC中僅此與ARMA(1,1)為次佳，綜合判斷,模型ARMA(1,0)為最佳階數。

2.1.3 ARMA模型檢驗

(1)自相關檢驗

本研究采用殘差序列相關LM法檢驗ARMA模型，選取滯后一至五階進行殘差相關檢驗。檢驗結果表明ARMA(1,0)模型異方差懷特檢驗量對應的P值均大于0.05，即殘差不存在序列相關，無遺漏變量，滯后階數選取合理。

表4 AIC、SIC和HQ方法信息表

Table 4 Information sheets of AIC,SIC and HQ method

模型Model AIC SIC HQARMA(1,0)-5.813 072-5.791 659-5.804 561ARMA(1,1)-5.813 082-5.780 962-5.800 316ARMA(0,1)-5.647 139-5.625 769-5.638 646ARMA(2,0)-5.812 695-5.780 510-5.799 902ARMA(2,1)-5.808 003-5.765 089-5.790 945ARMA(2,2)-5.808 007-5.765 094-5.790 949ARMA(0,2)-5.751 998-5.719 944-5.739 259ARMA(1,2)-5.807 812-5.764 986-5.790 790

注：粗體為最大值

Note:Bold are the maximum

(2)殘差白噪聲檢驗與正態檢驗

通過觀察該樣本殘差序列的ACF、PACF，判斷該殘差序列是否為白噪聲序列。

表5顯示，各期Q統計量對應P值均高于0.05，說明殘差序列是白噪聲序列。結合自相關檢驗與白噪聲檢驗，判定ARMA(1,0)模型已經將原序列中的信息提取完全，該模型擬合顯著。

表5 樣本殘差序列的ACF、PACF

Table 5 ACF and PACF diagrams of sample residual error sequence

2.2 GARCH模型研究

2.2.1 GARCH模型的建立

對已建立的ARMA(1,0)模型使用LM法檢驗判定模型是否具有ARCH效應，結果顯示，F統計值為4.637 139，異方差懷特檢驗量(Obs*R-squared)為4.603 694，F統計量的概率(Prob.F(1,391))為0.031 9，卡方檢驗的概率(Prob.Chi-Square(1))0.031 9。該結果表明模型存在1階ARCH效應，因此需要建立GARCH模型去除ARCH效應。GARCH模型使用最小信息準則對比如表6。由表6可知GARCH模型滯后階數(3,2)最小，選擇GARCH(3,2)模型，模型AIC=-5.864 8、SC=-5.768 4、HQ=-5.826 5。

表6 GARCH模型信息表

Table 6 Information sheet of GARCH model

GARCHAICSCHQ(1,1)-5.826 0-5.761 8-5.800 5(1,2)-5.823 8-5.748 8-5.794 0(1,3)-5.848 7-5.763 1-5.814 7(2,1)-5.820 3-5.745 3-5.790 5(2,2)-5.817 2-5.731 5-5.783 1(2,3)-5.819 4-5.723 1-5.781 1(3,1)-5.817 2-5.731 5-5.783 1(3,2)-5.864 8-5.768 4-5.826 5(3,3)-5.843 3-5.736 3-5.800 8

注：粗體為最大值。

Note: Bold are the maximum.

2.2.2 GARCH模型的檢驗

使用LM法檢驗GARCH(3,2)模型殘差是否仍具有ARCH效應，結果顯示，其F統計值為0.059 821(P=0.806 9)，異方差懷特檢驗量為0.060 143(P=0.806 3)。GARCH族模型異方差懷特檢驗量均大于顯著水平0.05，殘差序列不存在ARCH效應，因此此次研究建立的GARCH模型均滿足序列平穩且沒有ARCH效應的統計要求。

2.3 模型預測效果對比

結合前文基于南寧市2017年1月1日-2017年12月31日O3日均濃度監測值樣本數據建立的ARMA(1,1)模型-GARCH(3,2)模型，對南寧市2018年1月1日至2018年1月31日O3日均濃度進行預測，結合實測值進行誤差分析(圖3)。

結果表明，模型預測值與實測值的擬合趨勢基本一致，相對誤差率平均34.39%；在31 d預測濃度值中，有9 d與實測值相對誤差率在5%以內，有14 d與實測值相對誤差率在10%以內，有9 d與實測值相對誤差率在10%-20%，但也有8 d預測值與實測值誤差較大。從圖3可以看出，在實測值擬合曲線峰、谷值等前后位置容易出現較大誤差。2018年1月1日與1月2日的預測值相對誤差率均不超過4%，說明由于時間序列模型體現的是時間序列的自相關性和自身的動態記憶性，更適宜反映樣本時間序列的短期變化。

圖3 模型擬合效果圖

Fig.3 Chart of model fitting effect

3 結論

本文通過構建ARMA-GARCH模型，對南寧市城區2018年1月31 d的O3日均濃度進行預測，預測值擬合曲線基本能與實測值保持一致。在31 d預測濃度值中，23 d預測相對誤差率在20%，較為準確，其中2018年1月1日與1月2日相對誤差率均小于4%。這表明采用時間序列ARMA-GARCH模型短期預測O3濃度是比較有效的，能為O3濃度的預測預報提供一定的參考價值。

盡管時間序列ARMA-GARCH模型描述的是樣本在時間序列上的自相關性，可較為準確地反映短期內的時間序列變化關系，而非長期的變化關系。但正因如此，時間序列ARMA-GARCH模型更適宜應用在短期大氣污染物濃度預測方面，充分發揮其速度快、準確性較高的特點，為大氣污染防治提供決策參考。