復合載荷圓柱殼徑向接管極限載荷參數化分析

唐清輝 劉 坤， 桑芝富 李 沖

（1.江蘇釜鼎能源科技有限公司；2.南京工業大學機械與動力工程學院；3.南京曉莊學院電子工程學院）

圓柱殼接管結構通常受內壓、彎矩、扭矩及接管軸向推力等聯合作用，國內外許多學者對復合載荷作用下圓柱殼接管結構的極限承載能力進行了研究， 提供了許多有價值的研究成果，為此類設備的設計和制造提供了數據支持。Tabone C J和Mallett R H兩位學者對開孔率為0.65的帶接管圓柱殼結構在內壓與面外彎矩聯合作用下的極限載荷進行三維有限元分析［1］。 Moffat D G和Mistry J對大開孔圓柱殼接管結構進行研究，指出大開孔結構在內壓與接管彎矩聯合作用下極限載荷關系近似為二次方程［2］。 Nadarajah C等提出當模型d/D=0.1與d/D=0.2時， 內壓與面內彎矩聯合作用下小開孔接管結構的極限載荷相互影響關系近似為線性方程，當d/D=0.4時，極限載荷的相互影響關系近似為二次方程［3］。 Xuan F Z和Li P N對復合載荷作用下d/D≥0.5的圓柱殼開孔接管結構極限載荷進行有限元計算并總結出了經驗公式，在經驗公式中引入了幾何參數d/D、D/T、t/T，并對經驗公式進行驗證［4］。唐清輝等對在內壓和接管彎矩組合作用下的圓柱殼開孔接管結構強度進行了試驗研究和有限元分析，繪制了試驗模型內壓與接管彎矩組合加載工況下極限載荷關系曲線［5］。 徐心怡和賀小華采用應力分析法和極限載荷分析法，對在內壓和支管外力矩作用下的圓柱殼徑向開孔接管原結構、加強筋結構和接管根部加厚結構進行應力分析和評定，認為相較于原接管結構，加強筋結構在僅受內壓時承載能力無甚改善，在組合載荷作用下的承載能力有所增加［6］。

筆者在有限元求解基礎上， 考慮3個無量綱幾何參數d/D、t/T、D/T對圓柱殼開孔接管結構極限載荷的影響［7，8］，回歸出內壓與接管縱向彎矩聯合作用下帶徑向接管圓柱殼極限載荷關系的經驗方程，并對經驗方程進行驗證。

1 參數化分析模型

1.1 模型結構及幾何尺寸

參數化分析模型由圓柱殼、徑向接管、封頭及法蘭等部件組成，主要結構形狀如圖1所示，其中Di為圓柱殼內徑，L為圓柱殼長度，L1為圓柱殼長度的一半，T為圓柱殼壁厚，do為接管外徑，di為接管內徑，t為接管壁厚，l為接管長度。 帶徑向接管圓柱殼的極限承載能力與3個無量綱參數do/Di、t/T、Di/T有關［4，7，8］。 取參數化模型的尺寸Di為500、1 000、1 500mm，do/Di為0.2、0.4、0.6、0.8；t/T 為 0.25、0.50、0.75、1.00；Di/T為50、75、100、125。

圖1 主要部件模型結構

1.2 模型材料及力學性能

分析模型圓柱殼及其封頭材料為普通碳素鋼Q235-B，接管材料為20#鋼，在MTS試驗機上對上述材料進行拉伸試驗得到力學性能，詳見表1。

1.3 試驗方案設計

在圓柱殼直徑一定的條件下， 試驗共有3個因素do/Di、t/T、Di/T，每個因素取4個水平，按照正交試驗法三因素四水平的正交表組合，有16組模型，計算模型參數的正交表見表2，分別取圓柱殼直徑Di為500、1 000、1 500mm，共計48組模型。

表2 計算模型的正交參數表

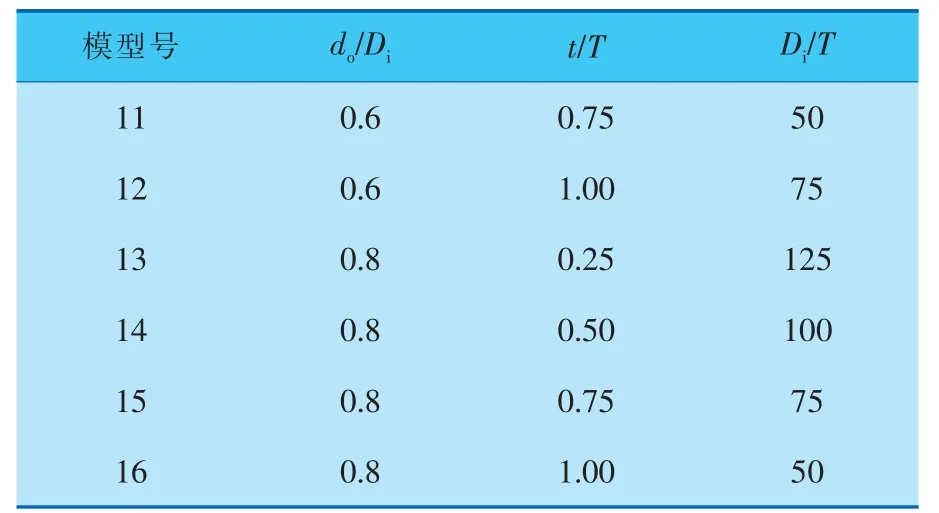
（續表2）

2 有限元計算

考慮到模型幾何形狀與載荷均對稱，選取實體模型的一半建立有限元模型進行分析。

2.1 單元選用及網格劃分

選用三維八節點solid45單元進行建模［7，8］，采用映射網格進行劃分， 考慮到圓柱殼開孔-接管區受力復雜，對該區域進行局部網格細分，細分范圍為距離焊縫2.5（R、T分別為圓柱殼平均半徑和壁厚）以內的區域［3］，在建模過程中考慮了連接圓柱殼與接管的角焊縫結構，且取角焊縫材料和圓柱殼材料相同［5］。 劃分網格后的有限元 模型如圖2所示。

圖2 有限元網格模型

2.2 邊界條件及載荷

在對稱面施加面對稱約束，內表面施加內壓載荷，圓柱殼的下端面固支，另一端保持自由，在接管端面上施加縱向彎矩載荷。

考慮到焊接殘余應力對圓柱殼接管結構塑性極限載荷的影響較小［9］，在有限元分析中沒有考慮焊接殘余應力。

2.3 材料模式

分析模型采用多線性等向強化材料模式［5］，該模式用多個應力-應變值連成一條曲線來模擬材料的特性曲線， 每種材料選用了包括屈服應力、屈服應變在內的10個點的應力-應變值，見表3。

2.4 極限載荷

根據計算得到不同復合載荷作用下有限元模型關鍵測點的應變值， 繪制載荷-最大主應變曲線，采用兩倍彈性斜率準則確定模型內壓與接管縱向彎矩聯合作用下的極限載荷［10］，最大主應變位置在圓柱殼縱向截面受拉側外壁面，得到計算模型的極限載荷見表4～6。

表3 多線性材料模式

表4 Di=500mm時內壓極限載荷P、縱向彎矩極限載荷M

（續表4）

表5 Di=1000mm時內壓極限載荷P、縱向彎矩極限載荷M

（續表5）

表6 Di=1500mm時內壓極限載荷P、縱向彎矩極限載荷M

（續表6）

3 極限載荷關系方程的回歸分析

回歸分析是研究隨機現象中變量之間關系的一種數理統計方法，它利用樣本數據來確定回歸模型參數，尋找變量關系的近似表達式［11］。

參照文獻［3］，擬定內壓與接管縱向彎矩聯合作用下極限載荷的關系方程形式為：

根據計算得到的內壓極限載荷和縱向彎矩極限載荷，利用STATISTICA軟件中非線性功能進行擬合，得到回歸方程如下：

當do/Di為0.2～0.4時

回歸方程（2）～（5）預測值與擬合殘差關系和殘差分布如圖3～6所示。 從圖3～6中可以看出，回歸方程的擬合殘差隨機地分布在零的兩邊，參數估計的誤差不關聯，擬合殘差分布基本符合正態分布規律（圖中紅色曲線），所以回歸模型是合適的。

圖3 回歸方程（2）的擬合殘差分布

圖4 回歸方程（3）的擬合殘差分布

圖5 回歸方程（4）的擬合殘差分布

圖6 回歸方程（5）的擬合殘差分布

4 回歸方程的驗證

4.1 有限元模型

筆者共設計了兩組有限元模型對上述回歸方程進行驗證，驗證模型的結構與圖1所示相同，有限元模型的材料也與前文所述相同，具體有限元模型尺寸見表7。

表7 有限元模型尺寸

4.2 驗證結果

分別采用回歸方程與有限元數值計算方法計算模型No.1、 模型No.2在內壓與接管縱向彎矩聯合作用下的縱向彎矩極限載荷見表8。 有限元模型在載荷單獨作用下的內壓極限載荷與縱向彎矩極限載荷分別為模型No.1，P*L=7.06MPa，=15.07kN·m； 模型No.2，P*L=6.67MPa，M*iL=143.50kN·m。

表8 回歸方程的驗證

從表8可以看出， 回歸方程與有限元計算結果是基本吻合的，最大誤差為9.77%，回歸方程可以用來預測圓柱殼開孔接管結構在內壓與接管彎矩聯合作用下的極限載荷。

5 結論

5.1 采用正交試驗設計、有限元模擬計算和回歸分析的方法，得出了do/Di在0.2～0.4和0.6～0.8條件下，內壓與接管縱向彎矩聯合作用下圓柱殼徑向接管結構極限載荷關系的經驗方程。

5.2 采用有限元計算結果對回歸經驗方程進行驗證和應用，證明了回歸方程的準確性，可為工程設計提供預測計算參考。

5.3 參數化分析法運用于復合載荷作用下圓柱殼接管結構極限載荷的求解是一種可行的方法，為快速求解多種載荷聯合作用下圓柱殼接管結構的極限承載能力提供了研究方向。