深度研讀教材策略一:還原數學知識的本質原理(2)
惠英杰 嚴秀麗 羅瑞

【導讀】
“單價、數量、總價”是人教版數學四年級上冊的內容。該部分內容在人教版的教材中曾被刪減,后又重新“回歸”。在被刪減的時期,似乎對于學生正確解答“購物”問題也沒有多大影響,但為什么現在又把它“請回來”了呢?其中有什么值得我們深入探尋的東西?它對學生數學學習的后續發展又有什么重要意義?
本案例中,作者以自己和同伴的實踐經驗和審慎思考,正面回答了以上問題。這或許能為大家提供一點有益的參考。
【案例】
課堂實錄:
一、情境導入
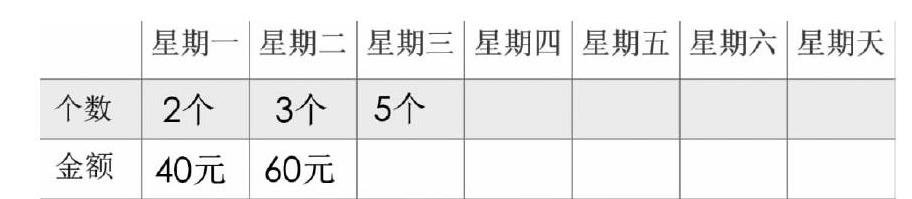
師:小紅家樓下有一個小賣部,生意很火熱。她連續6天調查了特百惠杯子的銷售情況。(出示調查表)
(生根據教師給出的個數或金額,逐步完成星期三到星期六的表格填寫)
師:看了這個調查表,你有什么發現?
生1:這些杯子都是每個20元。
生2:杯子賣出的個數多,收入的錢數就多;賣得少,收入的錢數就少。
生3:星期天的怎么還空著呢?
師追問:你估計星期天會賣出多少個?收入多少元?
……
二、理解單價
(一)認識單價
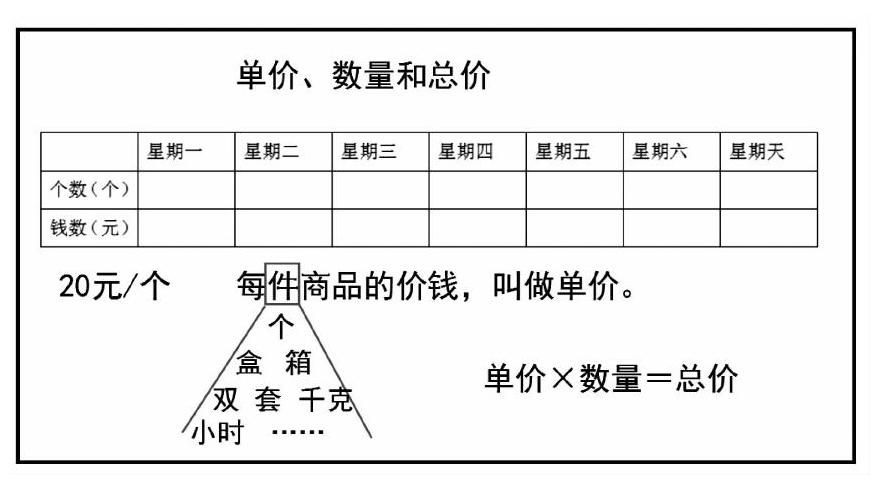
師:在購物中,我們把賣出商品的個數、件數……叫作數量。一共收入的錢叫作總價。
(師將表格中原來的“個數”替換為“數量”,“金額”替換為“總價”,生觀察)
師:如果杯子賣出的數量多,總價反而少;或者賣出的數量少,總價反而多。這樣公平嗎?
生(齊):不公平!
師:是什么神奇的力量,保證購物的公平性呢?
生:這些杯子都是一個20元,這是一個固定不變的數。
師追問:一個杯子是20元,這里說的“一個”是哪一個杯子?
生1:隨便哪一個。
生2:任何一個。
師:像這樣每一個杯子的價錢叫作這款杯子的單價。當我們只買一個杯子的時候,需要付出的總價是多少元?
生(齊):20元。
師:這里總價的“20元”和單價的“20元”就有點混淆了,是不是?
生(齊):是。
師:為了區分單價與總價,我們把單價寫成這樣的形式——20元/個,讀作“20元每個”或“每個20元”。(生跟讀)
師:你知道哪些商品的單價?能這樣規范地寫一寫嗎?
(生嘗試規范地寫出單價并在小組內進行交流)
師:猜猜這是哪種商品的單價?
(師給出不同的單價,生大膽猜測,氣氛異常活躍)
(二)表現形式
師:當我們把6個杯子裝成一箱,一整箱地進行銷售。這箱杯子應該賣多少元?
生:120元。
師:這里的120元是單價還是總價呢?
生1:表示總價。
生2:表示單價。
生3:既表示6個杯子的總價,也表示這一箱杯子的單價。
師追問:在這里,它表示什么更合適?
生3:表示單價更合適,因為它是整箱地賣。
(動畫演示:“120元/箱”變為“110元/箱”)
師:明明價值120元的6個杯子,為什么只標價“110元/箱”?
生:因為整箱地賣,賺錢更快,可以優惠顧客。
師:說得好!在實際生活中,很多商品批發和零售的單價是不一樣的。
師:你見過這樣表示的單價嗎?(出示生活中常見的各種單價)
誰來給大家解釋一下它是什么意思?
生1:這里的5元既可以看作10塊燒豆腐的總價,也可以看作這樣一份燒豆腐的單價。
(動畫演示10塊燒豆腐裝成一盤)
師:也可以換個說法……
生2(迫不及待):5元/盤。
師追問:那為什么不直接標價“5元/盤”?
生2:這樣更顯得“貨真價實”。
師:對!這樣標價能讓顧客更清晰地衡量商家有沒有“宰客”的嫌疑。
師:由此可見,一個錢數究竟表示單價還是總價,由什么來決定?
生:主要看購物過程中,以多少個商品為一份。
師:現在你能用自己的話說說什么是單價嗎?
生:每一份商品的價錢就叫作單價。
師補充:數學上,我們把每件商品的價錢叫作單價。(板書)
師追問:這里“每件”的“件”可以是哪些量詞?
生:個、盒、份、箱、小時、天……
三、歸納關系
師:知道了每個杯子的單價是20元,你能很快算出每天銷售杯子的總價嗎?
生:買了幾個就用20乘幾。
師追問:這里的“幾”可以是哪些數呢?
生:1、2、3、4……
師:如果用字母n表示數量,總價是多少元呢?
生:20×n。
師:你能用一個算式表示出單價、數量與總價之間的關系嗎?
生:單價×數量=總價。(師板書)
師追問:你能用乘法的含義解釋一下這個數量關系嗎?
生:單價相當于二年級學習乘法中的“每份數”,數量相當于“份數”,總價就是“總數”。
師補充:把若干個單價合起來就成了——
生(齊):總價。
師:看著這一組數量關系,又怎樣求出數量或者單價呢?你是怎么想的?
……
四、實際應用
師:說出下面各題是已知“單價、數量、總價”中的哪兩個量?求哪個量?.
(題略)
生:第一題是已知單價和數量,求總價,用乘法解答;第二題是已知單價和總價,求數量,用除法解答。
【課件出示】
農貿市場里的羊肉單價是68元/千克。張叔叔買了一些羊肉,花了34元。這可能嗎?
師:大家覺得呢?
生1:不可能,總價怎么會比單價還少呢?
生2:我覺得是可能的,張叔叔只買了半千克,所以只花了單價的一半。
師追問:“半千克”是幾千克?
生2:0.5千克。
師:那么還可以用“單價×數量=總價”來解答嗎?
生:應該可以的,用68×0.5=34(元)。
師:對了,這就是我們明年將要學習的小數乘法。
五、小結
什么是單價?單價、數量、總價之間有什么關系?
(生回答略)
板書設計:
【評析】
本節課是昆明市盤龍區周佳泉小學數學名師工作室全體成員經過近半年的苦苦摸索形成的集體智慧的結晶。其最顯著的特點是把重點放在了對單價意義的深刻理解和單價豐富表現形式的體驗上。在深刻理解了單價含義的基礎上,水到渠成地放手讓學生自己歸納單價、數量、總價之間的關系,并在實際應用中初步滲透了小數乘法的萌芽知識。回首來時路,在磕磕絆絆的摸爬滾打中,我們逐步清晰地認識到了這節課的價值所在:
1.單價并不簡單等同于每份數。從函數關系的角度來講,在單價、數量、總價三者之間的變化關系中,單價是恒定量(一定時空范圍內同一種商品的單價),數量是自變量,總價是因變量。這是單價區別于每份數最大的特點。
2.單價有著豐富的表現形式。當我們只買一個(件)商品的時候,所付出的錢數既是這款商品的單價,也是所購買商品的總價。當我們把若干個商品看作“一份”來出售的時候,這些商品的總價又重新構建成為更大數量為計價單位的單價。因此,單價和總價的關系是相對的。甚至直到現在,在某些地區還保留著“一元錢幾個(幾個/元)”的標價形式。
3.單價的本質與勞動價值有關。從純數學的角度來講,單價是總價與數量的比值(或反之亦可)。從生活的角度來講,單價其實相對客觀地反映了商品中所含勞動價值的多少。也就是一件商品中所含的勞動價值越多,它的單價相應地也會越高;反之則較低。
4.總價其實就是單價累加的結果。把若干個單價累加起來就得到總價,這是四年級學生普遍具有的數學經驗。教師需要做的是引導學生理解:單價累加可以在空間方向上(幾個、幾箱……)進行,也可以在時間方向上進行。單價累加可以以倍數級的方式進行(數量為整數倍),也可以以分率級的方式進行(總價有時小于單價),這為五年級學習小數乘法中積的大小變化規律和六年級學習“單位‘1”概念埋下了有益的種子。
5.可以用“四性”來加深對單價的理解。恒定性:在一定時空范圍內,一款商品的單價是相對恒定的;普適性:一款商品的每個個體都適用于這個單價,同時這款商品的每個個體質量也要適應這個單價;復合性:單價是總價與數量的比值,所以應當寫成復合單位的形式(盡管教材上不做硬性要求);豐富性:單價在生活中的表現形式多種多樣,單價與總價之間還會互相轉換,不同的單價適用于不同數量級的交易活動。當然,教師不可能在課堂教學中生硬地向學生灌輸這些專業知識,但可以通過恰當的情境載體進行有機滲透。
綜上所述,“單價、數量和總價”這節課在四年級的整冊教學內容中占有非常重要的地位。它對于滲透函數思想、培養學生用動態的眼光看待事物、培養學生在紛繁的表象下抽象出數學本質的歸納能力,具有舉足輕重的作用。

