空間細胞機器人面向桁架在軌攀爬步態分析

游斌弟，溫曉雷，劉育強，譚春林，安德孝，田 浩，趙 陽

(1. 哈爾濱工業大學(威海)船舶與海洋工程學院， 威海 264209； 2. 北京空間飛行器設計總體部， 北京 100094；3. 哈爾濱工業大學航天學院， 哈爾濱 150001)

0 引 言

空間機器人作為多學科的新興領域，能夠很好地適應空間環境，代替航天員進行艙外作業，降低維修成本，提高工作效率[1]。但是，目前已經服役的空間機械臂和空間機器人所能實現的功能是有限的，只能進行簡單的檢測與維修操作，而且工作空間有限容易受到臂長限制,很多時候需要在人機協作下完成空間任務[2]。空間細胞機器人(Cellular space robot, CSR)[3]是一種利用器官、組織、細胞之間的多層次結構，結合細胞的分裂與分化，設計出多種細胞單元，面向空間任務組裝成相應工作構型的新型空間操作裝置。它取自細胞衛星(CellSat)的概念，每種細胞單元之間都能實現標準可靠連接，利用細胞的集群效應和遷移效應，相比傳統模塊化機器人能夠適應更多的空間任務環境，擴展性大大提高，配上相應功能的末端執行細胞，完成不同環境下的空間任務[4-6]。

許多重要的配套器件需要安裝在航天器擴展的桁架結構上，細胞機器人必須具有在桁架結構上攀爬移動功能，以完成元器件的搬運以及裝配維修操作。目前針對在軌攀爬的研究較少，大多攀爬機器人都是進行地面操作，可分為滾動式[7-8]、吸附式[9-12]、夾爪式[13]等幾大類。還有一些學者從細胞的群體運動入手，利用材料的趨光特性作為機器人動力源進行移動，為攀爬機器人的研究提供了新的思路[14-16]。綜合分析，滾動式或環抱式的攀爬機器人比較適合無節點的單桿(筒)攀爬環境，不太適合多節點的桁架結構；仿生類吸附式很多針對的是平面移動工況，其負載能力通常是有限的；夾爪式的攀爬機器人利用其靈活特性可以很好地避開桁架節點，并且能夠夾持桁架桿等航天器件完成攀爬和裝配操作。

空間細胞機器人因其良好的變形特性可以靈活應對復雜的空間攀爬環境，很多學者在機器人構型表達方面進行研究。Hou等[17]提出一種C-Graph構型表達方式，在常規圖論的基礎上擴展出新的連接點和連接方向，通過序列式表達將構型變換方案進行序列配置，便于得到最優構型。王曉帆等[18]基于EMERGE模塊提出一種二進制狀態表，結合模塊特征得到一種新的關聯矩陣，能夠表達一些簡單構型。這些研究大多數都是集中在組成機器人構型的模塊單元種類、數量和連接關系上，對相鄰單元的連接方向、單元的姿態以及模塊關節的初始轉角描述較少。同時，大多數基于拓撲構型可以快速得到構型矩陣，但當由構型矩陣描繪拓撲構型時，就很難保證唯一性和快速性。

步態分析作為機器人運動策略選擇和運動規劃的基礎，一直是機器人攀爬運動研究的熱點。江勵等[19]針對三維桁架結構的單桿攀爬環境設計出尺蠖式、扭轉式和翻轉式三種步態，但對于多節點的桁架環境需要不斷的進行桿間過渡，增加了爬行難度和能量消耗。郁樹梅等[20]針對蛇形機器人的三維運動提出一種螺旋步態，能夠實現機器人姿態的三維重現，為步態設計提供了新的思路。趙京東等[21]采用三分支機器人針對單桿攀爬環境設計出兩種相應的步態，獲得了更快的移動速度，但是未考慮桁架節點干涉問題。由此可見，傳統的步態研究大多都是針對單桿環境的，對桁架結構多節點干涉問題的考慮較少，且沒有針對攀爬環境進行工況的劃分，導致不能滿足所有的攀爬任務需求，針對三維桁架的雙桿攀爬可以很好地解決這些問題。

針對以上研究現狀，本文基于空間細胞機器人理念，結合在軌攀爬任務需求提出幾種細胞單元，并對其進行基本描述，引入構型矩陣和組織遷移矩陣。綜合桁架結構和細胞機器人自身的特點，區別傳統工況，將其存在的攀爬工況進行更為廣義劃分，考慮模塊化特性，進行運動學分析。針對每種攀爬工況，提出相應的攀爬步態，通過數值仿真對比不同步態下細胞機器人的關節力矩、能耗以及末端軌跡所占據工作空間等參數，為細胞機器人在三維桁架上完成實際在軌攀爬和搬運操作提供了依據。

1 細胞單元與組織遷移描述

要使組裝完成的細胞機器人具有攀爬、運輸以及裝配等功能，整個細胞機器人至少需要連接細胞L、轉動細胞B以及末端執行器細胞S(對于攀爬只用到了手爪細胞)三類細胞單元，如圖1所示。

L細胞為正六面體結構，主要承擔細胞機器人的擴展功能，為了便于構型表達，將L細胞六個面進行標號，分別為1/10,-1/-10,2/20,-2/-20,3/30和-3/30，其中帶有右下標0的為被動連接面。B細胞主要承擔轉動功能，只有兩個連接面，用數字1/10和-1/-10進行表達。S細胞的主要功能是安裝末端執行器(手爪、鉆頭、攝像頭等)，只留一個面作為連接面，用數字-1/-10表示。為了增加整個細胞機器人的靈活性，每個連接面處有一個旋轉自由度。

圖1 三種細胞單元Fig.1 Three types of elementary cells

隨著攀爬環境的更換，細胞機器人必須具有變形能力，以三分支混聯機器人為例，其拓撲圖如圖2所示，混聯機器人中的支鏈可以看作由幾個細胞單元組成的組織。利用細胞單元的遷移特性，L9與L3相連，連接面F6斷開，組織可以快速從L5節點遷移到L3節點上，為了便于遷移之后構型的表達，重新排序后L9變為L7，B7變為B9。

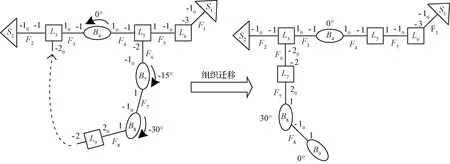
圖2 混聯機器人組織遷移拓撲描述Fig.2 Topological description of tissue migration for hybrid robots

在圖論關聯矩陣[22]的基礎上進行改進得到一種適合此細胞機器人的遷移矩陣。用細胞單元表示關聯矩陣中的頂點，用連接面表示關聯矩陣中的邊，分別用細胞倉庫矩陣N和連接面矩陣F來表達：

(1)

(2)

式中：Li/Bi/Si表示連接、轉動、末端執行細胞中的任意一個，代表了細胞單元的種類；n表示細胞單元的數量；Fi表示第i個連接面。

其細胞遷移矩陣G如下所示：

(3)

L,B和S細胞初始姿態保持如圖1所示，引入連接面處的轉角α以及細胞單元自身的轉角γ，保證構型的唯一性。將細胞單元和連接面在全局空間中從1到n(n-1)按照從左到右(y軸正向)，從上到下(x軸正向)，從頂層到底層(z軸負向)的方式排列，如圖2所示，保證了由構型矩陣到拓撲構型轉換的快速性。細胞遷移矩陣即能準確表達遷移前后的細胞機器人構型，又能很好地表達組織遷移過程。

2 攀爬運動分析

2.1 攀爬工況

長方體桁架的每個面和每條邊上的點都可能成為機器人的攀爬面和夾持點，需要對其攀爬工況進行廣義劃分，使其能夠滿足所有攀爬任務需求。基于一致性、重復性和容易控制原則，采用雙手爪對稱構型的細胞機器人，為了避免單桿攀爬中存在的節點干涉問題，采用雙桿攀爬工況，結合空間桁架特點將攀爬工況分為三類——橫攀工況、縱攀工況和斜攀工況，如圖3所示。

橫攀工況：手爪夾持點為Ai，沿著兩平行桿進行橫向交替運動。

縱攀工況：手爪夾持點為Bi，進行攀巖式縱向交替運動。

斜攀工況：手爪夾持點為Ci，細胞機器人夾持兩交錯桿中點進行交替運動。

攀爬過程中手爪夾持點所在的位置具有規律性，橫攀工況相鄰兩個夾持點(Ai)之間的距離是一致的，斜攀和縱攀工況下的夾持點(Bi和Ci)都為桁架桿的中點。

圖3 桁架攀爬工況Fig.3 Climbing conditions of truss

2.2 運動能力分析

考慮模塊化特性，采用基于旋量理論的指數積公式進行運動學分析。

具有n個關節變量的指數積公式為：

(4)

(5)

逆解問題可以劃分為以下三類子問題：

Ⅰ類子問題：如圖4(a)所示，已知起點p1和終點q1兩點，以及旋轉軸方向L1，可以求指數積方程e[L1]θ1p1=q1的解θ1。

Ⅱ類子問題：如圖4(b)所示，已知p2,q2兩點以及L2,L3，可以求e[L2]θ2e[L3]θ3p2=q2的解θ2,θ3。

這三類子問題的求解過程已經有大量研究，此處不再贅述。

圖4 細胞單元Fig.4 Elementary cell

1)目標點位姿求解

不失一般性，如圖5所示帶有分支的混聯機器人，當給定各個關節角可以求出末端執行器目標點位姿，{O}為基坐標系，{Oi}為分支點坐標系，{T1}、{T2}為末端執行器坐標系。結合式(1)可知Li/Bi表示L,B細胞中的一個，Lii/Bii表示分支點Li的支鏈中細胞單元的種類，S細胞只能位于機器人的首尾兩端。

假設機器人主鏈由m個L細胞，n個B細胞，k(1≤k≤2)個S細胞組成，則末端執行器T1的初始位姿：

(6)

式中：l為連接細胞的長度,l0為末端執行器的長度。

每增加一個L或S細胞就增加一個繞y軸的旋轉自由度θζ，其旋量指數矩陣：

(7)

式中：c代表cos，s代表sin。

每增加一個B細胞單元，忽略連接面自由度，增加一個B自身旋轉自由度θj，其旋量指數矩陣：

(8)

ryj=(mj+2nj+kj+1)l+kjl0

(9)

式中：mj,nj,kj分別表示第j個轉動關節前具有L,B,S細胞數量。

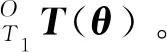
分支點坐標系{Oi}相對于{O}的初始位姿：

(10)

式中：mi,ni,ki分別表示分支點Li前具有L,B,S細胞數量。

(11)

2)可達能力分析

為了驗證末端執行器能否到達目標夾持點，需要進行運動學解耦，只有特定的構型才能得到封閉解，以圖6所示構型為例進行可達能力分析。

圖6 細胞機器人構型Fig.6 Configuration of CSR

已知T1目標位姿，式(4)可以寫成：

(12)

由于r2在軸線L1和L2上，r4在軸線L4和L5上，所以滿足e[V1]θ1e[V2]θ2r2=r2，e[V4]θ4e[V5]θ5r4=r4。

結合式(12)得到：

e[V1]θ1e[V2]θ2e[V3]θ3r4=Tr4

(13)

兩邊同時減去r2，得到：

e[V1]θ1e[V2]θ2e[V3]θ3r4-r2=e[V1]θ1e[V2]θ2·

(e[V3]θ3r4-r2)=Tr4-r2

(14)

利用等式兩邊模長相等，得到：

(15)

式(15)就轉化為了第Ⅲ類子問題，由此可得θ3，并結合式(13)可得：

e[V1]θ1e[V2]θ2(e[V3]θ3r4)=Tr4

(16)

式中：e[V3]θ3r4和Tr4為Ⅱ類子問題中p2，q2，利用Ⅱ類子問題可以求出θ1和θ2。

由式(12)可得：

e[V4]θ4e[V5]θ5=e-[V1]θ1e-[V2]θ2e-[V3]θ3·

(17)

由于r5在軸線L5上而不在軸線L4，可得：

e[V4]θ4e[V5]θ5r5=e[V4]θ4r5=Tar5

(18)

利用Ⅰ類子問題可以求出θ4。由式(17)可得：

e[V5]θ5=e-[V1]θ1e-[V2]θ2e-[V3]θ3e-[V4]θ4·

(19)

Tb和關節5的方向已知，由此可以求出θ5。

已知θ1,θ2,θ3和T2目標位姿，結合式(11)得：

(20)

(21)

采用求θ4和θ5的方法可求出關節變量θ6和θ7。

當解得θ1～θ7在關節變量的極限范圍之內時，說明末端執行器T1和T2能夠到達目標夾持點。

2.3 攀爬步態描述

追求控制簡單，考慮攀爬的交替性和重復性，細胞機器人構型為雙手爪五自由度對稱構型(去掉圖6分支)，設計橫攀工況的攀爬步態如圖7所示。

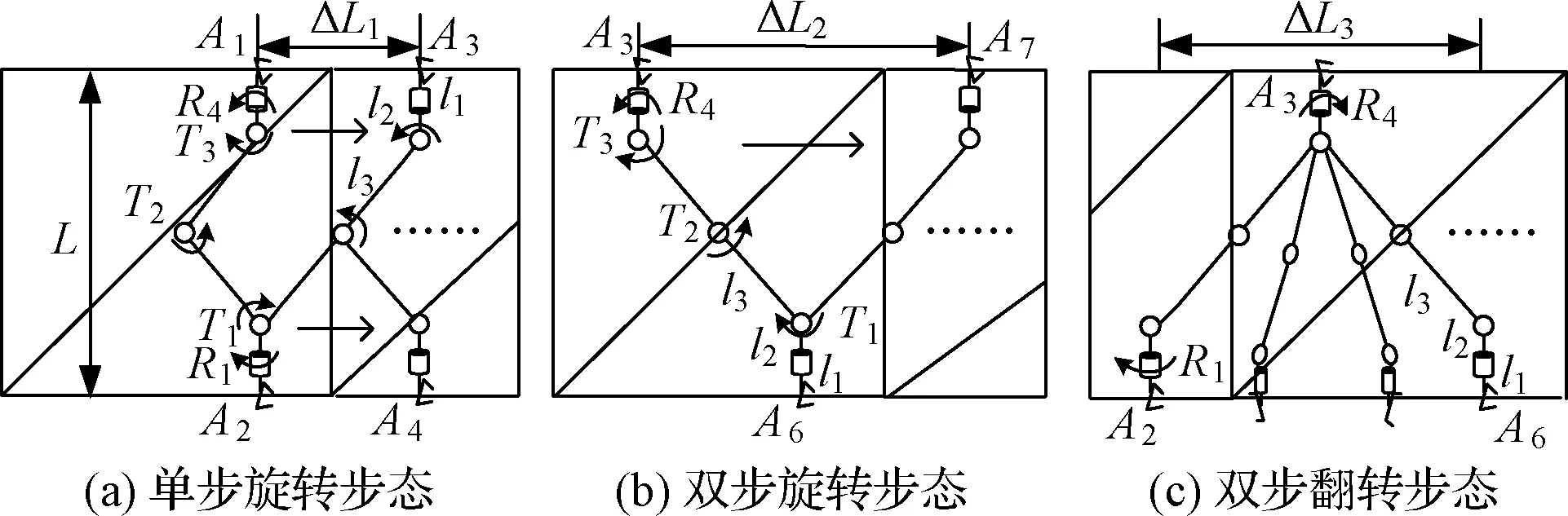
圖7 橫攀步態Fig.7 Gait of horizontal climbing

橫攀單步步態如圖7(a)所示，具體攀爬過程如下：

(1)機器人位于初始狀態，兩手爪斜攀于桁架平面，A2端手爪夾緊，A1端手爪松開。

(2)扭轉關節R4轉動60°，使手爪脫離桁架桿，然后旋轉關節T1,T2,T3轉動，使A1端手爪右移到最大距離A3點處。

(3)交換夾持端，A3端夾緊，A2端松開，控制關節R1,T1,T2,T3進行轉動，回到初始狀態，重復步驟(1)～(3)。

如圖7(b)所示，雙步旋轉步態與單步步態相比，參與運動關節相同，步距發生改變，A3端手爪直接移動到A7點處，然后互換夾持端，進行下次循環。

如圖7(c)所示，雙步翻轉步態與雙步旋轉步態相比只改變了手爪從A2到A6點的工作關節，控制扭轉關節R1,R4轉動180°，然后進行下次循環。

設計縱攀工況下的攀爬步態如圖8所示。

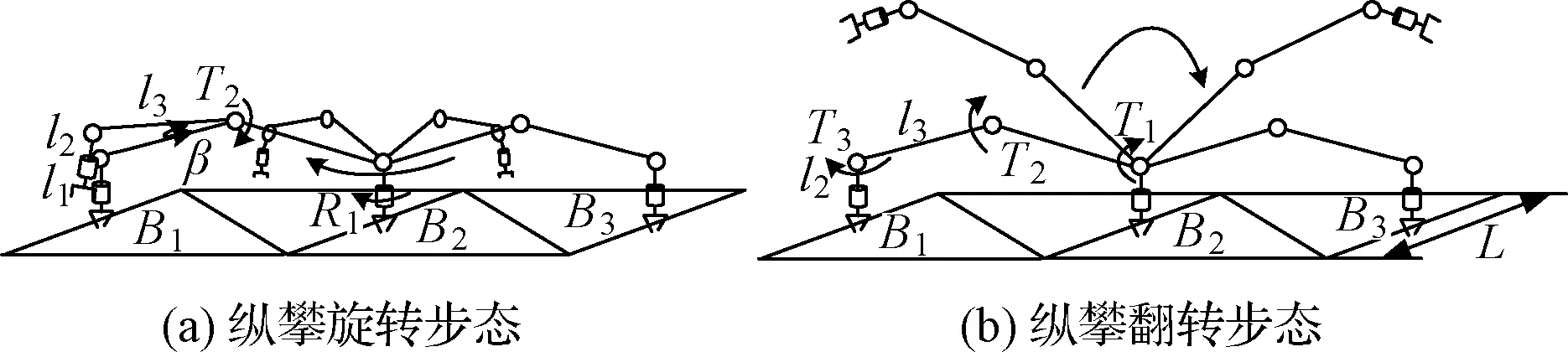
圖8 縱攀步態Fig.8 Gait of vertical climbing

縱攀旋轉步態如圖8(a)所示，具體攀爬過程如下：

(1)兩手爪斜攀于桁架平面，B2端夾緊，B1端松開，控制關節T2轉過角度β，使B1端手爪完全脫離桁架桿。

(2)扭轉關節R1以B2端手爪為軸線轉動180°。

(3)T2反向轉過角度β，互換夾持端，進行下一次循環。

如圖8(b)所示，縱攀翻轉步態與旋轉步態相比，只是改變了手爪從B1到B3點的工作關節，旋轉關節T1,T2,T3繞順時針方向旋轉完成縱攀過程。

縱攀工況下每步的夾持點都是固定的，每步移動的距離也是一定的，ΔL縱=2L。

設計斜攀工況的攀爬步態如圖9所示。

圖9 斜攀旋轉步態Fig.9 Rotating gait of oblique climbing

(1)兩手爪位于桁架桿中點斜攀于桁架平面，關節T1,T3初始轉角為90°，C2端夾緊，C1端松開。

(2)控制關節T3轉過角度θ1(見圖9(a))，C1端手爪脫離桁架桿，控制扭轉關節R1順時針轉動90°，最終達到狀態如圖9(b)所示。

(3)互換夾持端，達到圖9(c)所示狀態，進行下一次循環。

由于每步都保證夾持點位于桁架桿的中點，則步距ΔL=L。

3 步態仿真校驗

針對細胞機器人攀爬過程，作如下可行性討論：

1)每種細胞單元的設計尺寸，能夠滿足其所采用的驅動方式的空間幾何尺寸需求。

2)細胞機器人的拓撲構型，能夠滿足其所面向的空間應用環境。

3)不考慮重力因素影響。

取桁架桿桿長L=1100.00 mm，攀爬機器人桿長l1=70.00 mm，l2=140.00 mm，l3=420.00 mm，由三種細胞單元組成的桿長質量m1=1.25 kg，m2=2.5 kg，m3=7.5 kg，橫攀單步步態的步距ΔL1=493.15 mm，完成一次步距位移的時間取為20.0 s，為了保證數據的可比性，需要讓每種步態在相同的時間內移動相同的距離，橫攀雙步旋轉與雙步翻轉步態的步距都為2ΔL1=986.3 mm，設置時間為40.0 s。橫攀與斜攀工況下的機器人構型一致，只是利用其模塊化特性改變了手爪的位置，縱攀步態的步距都為2200.00 mm，設置時間為89.2 s，斜攀旋轉步態的步距為1100.00 mm，設置時間為44.6 s。

本文采用一種簡單等效算法[23]，用能耗表述值Q估計能量消耗。

(22)

式中：τi表示參與運動關節力矩，單位N·mm；t0表示完成一次步距位移所用的時間，單位s。

3.1 攀爬運動數值分析

如圖10所示，橫攀工況的三種步態均能很好地避開桁架節點，單步步態和雙步旋轉步態的移動端手爪均在與桁架平面平行的平面上運動，末端軌跡占據的工作空間較小，雙步翻轉步態的末端軌跡為半圓弧，占據的工作空間較大。由圖11可知，單步步態所需的最大關節力矩為550.37 N·mm，雙步旋轉步態為52.73 N·mm。單步步態最大力矩關節T1與雙步旋轉步態最大力矩關節T3規劃方式相同，轉角相同，轉動時間不同，T1角加速度大于T3，慣性張量相同，則雙步旋轉步態的最大關節力矩小于單步步態的最大關節力矩。同樣，雙步翻轉步態的最大關節力矩R4小于雙步旋轉步態的最大關節力矩T3。

圖10 橫攀工況仿真Fig.10 Simulation of horizontal climbing conditions

圖11 不同攀爬工況最大驅動力矩Fig.11 Maximum joint torque of CSR for different climbing gait

圖12 縱攀和斜攀工況仿真Fig.12 Simulation of vertical and oblique climbing conditions

如圖12所示，可以看出縱攀工況夾持點位于桁架桿的相同點，能夠很好地完成交替運動，但其末端軌跡所占據的工作空間都是比較大的。由圖11可知,兩種步態下的最大關節力矩分別為104.46 N·mm和66.61 N·mm。細胞機器人在無重力環境攀爬過程中主要克服慣性力，關節力矩與慣性張量有關，縱攀翻轉步態的T3關節慣性張量較小，理想情況下導致其驅動力矩非常小，所以無負載情況下，距離移動端手爪越近的關節，力矩通常越小。

斜攀工況每次攀爬的夾持點都位于桁架桿的中點，保證了步態的一致性和重復性，由圖13可知,斜攀旋轉步態驅動力矩的最大值為103.25 N·mm。T3關節轉動時，會對R1關節產生擾動，所以在0～5.57 s和39.03～44.6 s的時間內，關節R1的驅動力矩不為0。

圖13 斜攀旋轉步態各關節驅動力矩Fig.13 Joint torque of CSR for rotating gait of oblique climbing

3.2 不同攀爬工況綜合分析

空間桁架上通常會安裝一些大型航天元器件(太陽能電池板、散熱器等)，所以攀爬機器人末端軌跡占據的工作空間不能太大，否則容易產生干涉。由圖14可知，橫攀單步步態和雙步旋轉步態的末端軌跡所占據的工作空間較小，縱攀工況的步態占據工作空間較大。分析不同攀爬工況機器人驅動力矩的大小，只需比較每種步態最大的關節驅動力矩即可，由圖11可知,橫攀單步步態所需驅動力矩最大，橫攀雙步翻轉步態的驅動力矩最小，由于細胞機器人工作在空間環境中，在不考慮摩擦的情況下，關節做功主要克服慣性力，所以三種攀爬工況所需的驅動力矩都不是太大。利用式(22)來近似表述不同步態能耗的多少，計算結果如表1所示，橫攀雙步翻轉步態消耗的能量最少，橫攀單步步態消耗的能量最多。

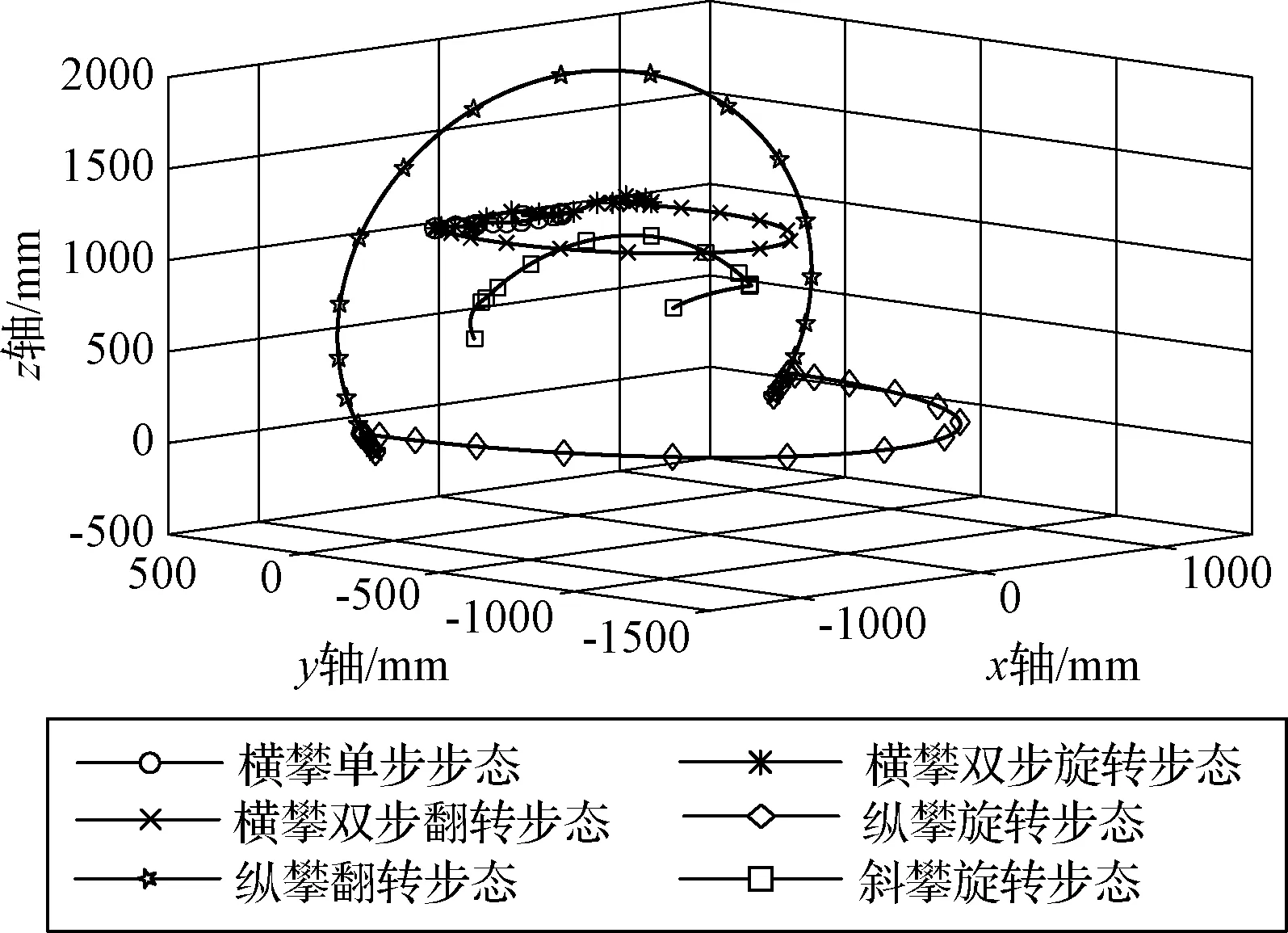
圖14 末端軌跡占據的工作空間對比Fig.14 Comparison of the workspace occupied by the end trajectory

表1 能耗對比Table 1 Comparison of energy consumption

上述幾種步態均能夠很好地避開桁架節點，滿足三維桁架的攀爬工況，實現交替重復性運動。在實際攀爬過程中，空間環境總是比較復雜的，針對不同優化目標選擇適合的步態：1)當目標點的距離較遠，則需要大步距的步態，橫攀單步步態之外的其它步態都可以選擇；2)當要求控制方式簡單(參與的關節少)，適宜選用斜攀旋轉步態和縱攀旋轉步態；3)當遇到障礙物較多的環境，攀爬機器人末端軌跡占據的工作空間應該最小，橫攀單步步態和橫攀雙步旋轉步態是很好的選擇；4)當要求力矩最小和能耗最優，最宜選擇橫攀雙步翻轉步態。

4 結 論

1) 針對空間在軌裝配、維修過程中的攀爬移動問題，基于細胞機器人理念，提出連接細胞、旋轉細胞和末端執行器細胞三種基本細胞單元，相比傳統的模塊化機器人，具有更加靈活的細胞單元模塊，利用細胞的集群效應擴展性大大提高。

2) 基于圖論和拓撲學原理在關聯矩陣的基礎上進行改進，得到一種既能描述遷移前后細胞機器人構型又能描述組織遷移過程的細胞遷移矩陣，確定了細胞單元種類和數量、連接面信息、細胞單元的初始姿態、空間順序以及關節旋轉角，保證了構型表達的唯一性。

3) 將三維桁架結構劃分出橫攀、斜攀以及縱攀三種廣義的攀爬工況，能夠滿足所有攀爬任務需求，針對每種工況提出相應的攀爬步態。步態仿真結果表明，這些步態都能夠很好地避開桁架節點，實現交替重復性運動，滿足一致性要求。不同步態的關節力矩、能量消耗以及末端軌跡所占據的工作空間是不同的，針對不同的應用環境和優化目標，選擇相應的步態。在無重力和末端無負載的工況下，所需關節力矩都比較小，短構型空間機器人在軌攀爬移動過程中關節力矩可以不作為其主要優化目標。