基于分數階微分算子的數字圖像邊緣檢測

郭琳琴，楊 艷，馬浩東

(呂梁學院 數學系，山西 離石 033001)

0 引言

圖像的邊緣中包含了豐富的視覺信息，在圖像分割、圖像特征提取、模式識別中有重要的意義，圖像的邊緣檢測是圖像處理中應用最為廣泛的研究課題之一.傳統的邊緣檢測算子多為微分算子，主要包括Rebort算子、Sobel算子等一階微分算子和Lapllician算子、LOG算子等二階微分算子.

近年來，分數階微分算子被廣泛應用于圖像處理過程中，并逐漸成為一個研究熱點.文獻[1]中楊柱中等人提出一種基于0～1階分數階微分的Tiansi掩模算子，該算子可有效的提取圖像的邊緣信息且有較高的信噪比；文獻[2]中王衛星等人進一步的改進了Tiansi掩模算子，使得圖像的邊緣檢測中紋理細節得到有效增強；汪成亮等人在文獻[3]中針對分數階數階數需要人為指定的缺陷，提出了一種自適應的算法；文獻[4]中蔣偉等人為了在銳化圖像邊緣的同時增強紋理細節特征，結合分數階與整數階微積分理論，推導出了新的有理數階微分.

本文提出的分數階圖像邊緣檢測模型，將能量泛函式中的導數改為分數階導數，然后用差分格式對其進行逼近求解從而分別構造水平、垂直和對角線分數階邊緣檢測微分算子，最后將這些算子合成為新的分數階邊緣檢測算子.

1 相關理論

1.1 分數階導數

分數階導數目前有三種經典定義：Riemann-Liouville(R-L)、Capotu(C)和Grumwald-Letnikov(G-L)，其中 G-L分數階導數定義為

(1)

1.2 分數階導數的差分格式

式(1)中h=1時，G-L分數階導數可以用有限項的分數階差分近似表示，即：

(2)

將上式推廣到二維，即可得到f(x，y)的分數階偏導數定義：

(3)

(4)

進一步可得差分近似表達式：

特別地，當v=1時，上式變為一階微分的差分近似表達式，

當v=2時，上式變為二階微分的差分近似表達式，

可見分數階微分是一階與二階微分的推廣形式.

2 基于分數階的圖像邊緣檢測算子

2.1 模型的建立

引入文獻[5]中能量泛函式：

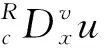
利用變分法推得的該泛函歐拉-拉格朗日方程如下：

其中，

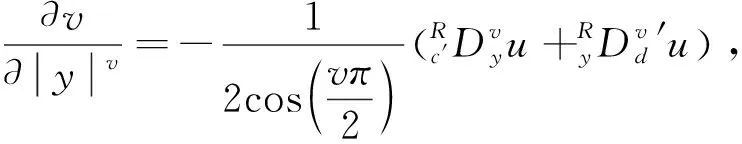
則，有如下結果

(5)

(6)

(7)

利用梯度下降法得到相應的擴散方程：

(8)

對上式離散化，有

其中，

2.2 分數階微分算子構造

構建水平方向和逆對角線方向整數階掩模算子，如圖1.

000-a0a000

(a)水平方向整數階算子

(b)逆對角線方向整數階算子

圖1水平方向和逆對角線方向上的整數階算子

以圖1(a)構造微分算子：a(f(x+1，y)-f(x-1，y))

則有x軸方向分數階微分算子如圖2(a)所示，旋轉對稱可構造y軸方向大小為3×3的分數階微分算子，如圖2(b)所示.

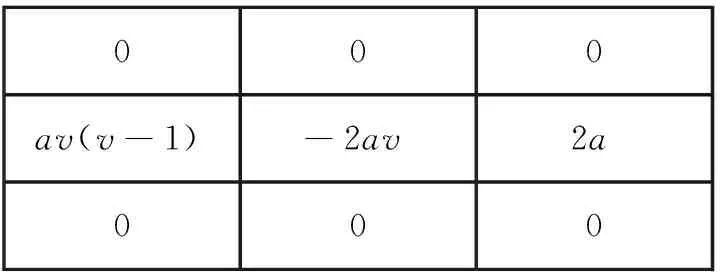
000av(v-1)-2av2a000

(a)x軸方向上的分數階算子

(b)y軸方向上的分數階算子

圖2水平、垂直方向上的分數階微分算子

以圖1(b)構造微分算子：a(f(x+1，y-1)-f(x-1，y+1)),有G=a(f(x+1，y-1)-f(x-1，y+1))

為了使得具有對稱性，做如下變形

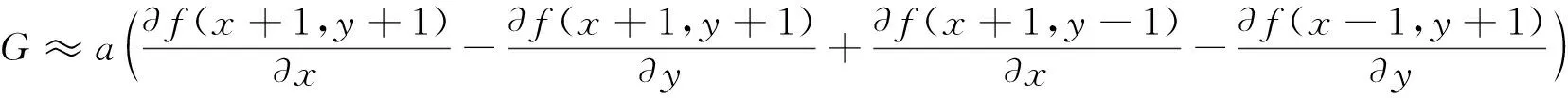
化解后可得

即可得逆對角線上分數階算子如圖3(a)，旋轉對稱可構造正對角線上的分數階算子如圖3(b).

0-av-a(v2-v-2)2av0ava(v2-v-2)2-av0

(a)逆對角線方向上的分數階算子

(b)正對角線方向上的分數階算子

圖3不同方向上的分數階微分算子

將所得的4個微分算子相加，即可得到3×3的分數階微分算子w，如圖4所示.

-a(v2-v-2)2-av(v-1)-a(v2-v-2)2av(v-1)02aa(v2-v-2)2-2aa(v2-v-2)2

圖4分數階微分算子w

2.3 基于分數階微分算子的邊緣檢測

設g(x，y)為灰度圖像函數，利用分數階微分算子w對圖像進行邊緣檢測的具體過程如下：

step1 對圖像g(x，y)進行去噪聲預處理，得到g(x，y)；

step2 選取適當的v，利用分數階微分算子w對圖像g(x，y)進行卷積運算，得到e(x，y)；

Step3 選取適當的閾值，對e(x，y)進行二值化處理，即可得到最終的邊緣檢測結果a；

該過程中，分數階參數v的選擇決定圖像邊緣檢測的效果，在實際操作中需要多次實驗調整.

3 實驗結果

實驗在MATLAB2019軟件環境下選取圖5(a)作為原圖完成.得到不同a值和不同v值下的圖像邊緣檢測結果，如圖5和圖6.

圖5 不同v取值下圖像邊緣檢測實驗結果

圖6 不同a取值下圖像邊緣檢測實驗結果

圖5實驗是在a=3時選取不同的v檢測的結果，可以看出當v值從0.4開始接近于0.7時邊緣檢測結果逐漸變好，可以較好的檢測到圖像的邊緣，當v值大于0.7時邊緣檢測結果清晰度略有下降，可見本文算法在合適的v值下的邊緣結果可以保留原圖像的特征，在視覺上有較好的效果.

圖6實驗是在v=0.7時選取不同的a值檢測的結果，可以看出當a值逐漸增大時邊緣信息逐漸增多，但當a選取過大時則會引起背景區域中的偽邊緣較為明顯的情況.

4 結束語

本文提出了一種基于分數階偏微分方程的圖像邊緣檢測模型，模型中將整數階微分算子中的二階導數變分為分數階導數，從而構造了包含水平、垂直、正對角線、負對角線四個方向梯度的分數階微分算子.實驗仿真結果表明，該算子能較好保留圖像的邊緣信息和紋理細節特征，對弱紋理圖像也可得到較為清晰的邊緣檢測結果，是一種可行的數字圖像邊緣檢測算法模型.實驗結果還表明檢測過程中的參數需要多次調整，如何自適應地選取參數以保證較好的檢測效果仍有待進一步討論研究.