金屬基外延石墨烯相圖非諧效應探討*

高君華，鄭瑞倫

(重慶文理學院 電子信息與電氣工程學院，重慶市高校新型儲能器件及應用工程研究中心，重慶 402160)

0 引 言

固體材料的相變不僅是固體材料的最基本的性質之一，而且是獲取各類新材料的重要途徑[1,2]。各類相變的條件、特點、遵從的規律是研制各類新材料和應用中需要解決的重要問題，對固體材料相變及其相圖的研究，是人們感興趣的一重要問題。早在上世紀四十年代，為了研究鐵磁-順磁相變，提出了伊辛(Ising)模型和海森堡(Heisenberg)模型；1963年文獻[3]發現在NaNO2這種亞鐵磁性材料中還出現非諧波效應驅動的拓撲相變。為了從理論上論述固-液-氣相變的特點，1980年文獻[5]提出二維Colling模型，此后，1983年文獻[5]提出了二元合金的二維Bernal晶格模型，用于研究二元合金的結構相變。1996年作者在文獻[6]中對二維Bernal模型進一步完善，用它研究了二元合金的的溶解限曲線。2018年Tong等在文獻[7]中研究了PbO2中出現的不可約相變。最近文獻[8]研究了在鍺中的相變。上述研究涉及的均為原子組成結構狀態的變化，即結構相變，未深入到原子組成結構不變而電子狀態變化的問題。

自2004年石墨烯制備成功以來，由于石墨烯具有優異的電學、力學和熱學等性質和二維結構，引起國內外的高度重視并對石墨烯做了不少研究。與單層石墨烯相比，外延石墨烯更與實際接近，研究它的性質更有現實意義，目前已對外延石墨烯的制備和性能進行了大量的研究。除對其制備以及熱學、電學性質進行研究外[9-11]，2014年文獻[12]和2015年文獻[13]對石墨烯在原子組成結構不變而電子狀態變化的轉變問題進行研究，證明單層石墨烯在考慮到電子自旋后，石墨烯這種由兩種子格組成的復式格子，由于原子內部電子相互作用能(內部關聯U)和原子間電子相互作用能(外部關聯G)的變化，電子系統狀態可處于三種狀態，石墨烯表現不同的電磁性質：一種是半金屬態(PM態)，此狀態中每個原子相應于一個具有零自旋磁矩的電子，電子能譜無能隙，材料具有半金屬性；第二種是自旋態度波態(BC態)，此狀態中原子的電子按子格均勻電荷和自旋分布，兩子格電子填充數相等，而自旋磁矩方向相反，系統表現為反鐵磁性，電子能譜具有能隙；第三種是電荷密度波狀態(BZ態)，這種狀態中電子仍按子格非均勻電荷和自旋分布，但兩子格電子填充數不等，系統表現為順磁性。BC態和BZ態是莫特絕緣體，而PM態是半金屬。但該文獻未對相變的條件、特點作研究，而且單層石墨烯難于實現。2017年Davydov在文獻[14]中證明：金屬基外延石墨烯中仍存在BC、BZ和PM三態，并研究了這三態的范圍，定性討論了相圖的性質。但文中認為原子靜止，未考慮到原子作非簡諧振動，其結果顯示不出溫度的影響，不能解釋在較寬的溫度范圍內外延石墨烯存在半金屬-反鐵磁-順磁，半金屬-絕緣相變的性質。為此，本文考慮原子振動的非簡諧效應，建立更完善的物理模型，應用固體物理理論，研究金屬基外延石墨烯電磁相變的特點和原子非諧振動對相圖的影響。

1 物理模型

我們研究的系統是在金屬基底(如Ni)上吸附碳原子形成由A子格和B子格組成的六角形結構的單層外延石墨烯復式格子，最近鄰原子間距離為d。取平面為OXY平面，坐標系選取如圖1。

A、B子格原子中的電子均具有自旋，自旋為?/2的狀態用↑表示，而自旋為?/2的狀態用↓表示。A子格原子中自旋為?/2的狀態電子填充數記為φ(d)，而自旋為?/2的狀態填充電子數為δ=d-d0；同樣，B子格原子中自旋為?/2、-?/2的狀態填充數為ε0，按照電子填充情況，系統會出現如下3種狀態：第一種，A、B子格的原子電子總數相等，但A、B子格原子自旋向上與自旋向下的電子數的差不等，即：ε1、ε2如圖2(a),這種狀態稱為自旋密度波狀態(BC)；第二種，A、B子格原子的電子總數不等，但A、B子格原子自旋向上與向下的電子數的差相等，即

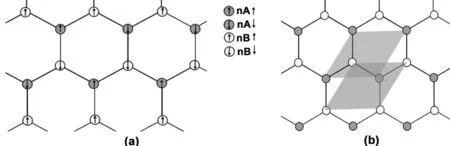
圖1 金屬基外延石墨烯中電子自旋示意圖Fig 1 Schematic diagram of electron spin in metal-based epitaxial graphene

nA↑+nA↓≠nB↑+nB↓，

nA↑-nA↓=nB↑-nB↓，

這種狀態稱為電荷密度波狀態(BZ)，如圖2(b)所示 ；第三種，A、B子格兩種原子的電子數和自旋向下與自旋向下的電子數的差均相等，即

nA↑+nA↓=nB↑+nB↓,

nA↑-nA↓=nB↑-nB↓,

這種狀態稱為半金屬(PM)，如圖2(c)所示。

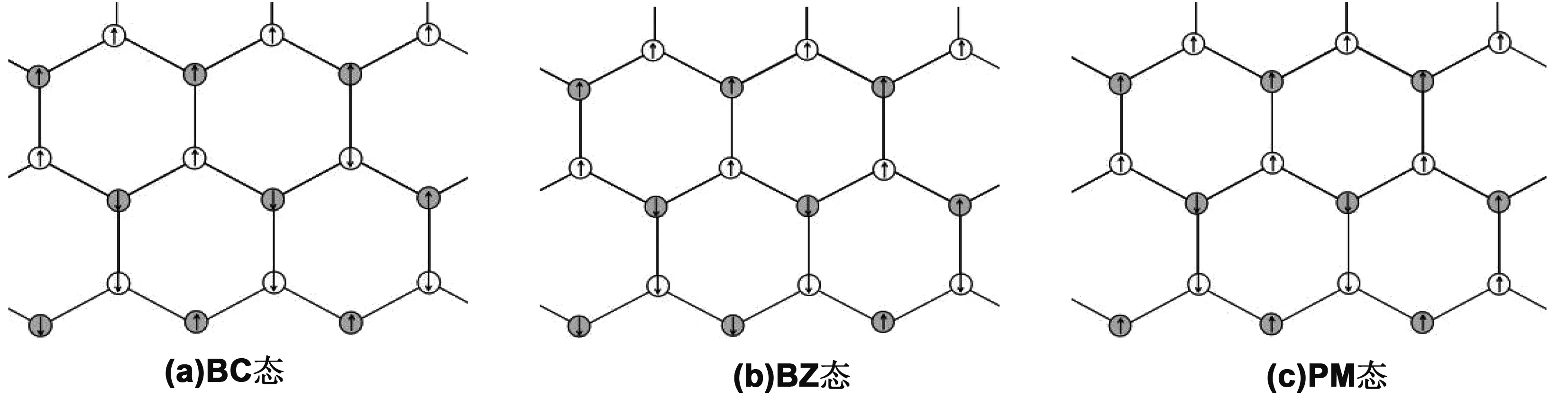
圖2 金屬基外延石墨烯A、B子格的3種狀態的自旋取向Fig 2 Spin orientation of three states of A and B sub-lattices of metal-based epitaxial graphene

為了描述系統狀態，引入序參量：a、b、c、d：

(1)

按此定義，a描述總電子數的多少；b描述A、B子格兩種原子自旋向上的總電子數與向下總自電子數的差，b>0，表示向上總電子數多于向下得到數；c描述A子格原子與B子格原子的電子數的差，c>0表示A子格原子的電子數多于B子格；d表示A、B子格的自旋向上與向下數目的差異程度，d>0表示A子格原子的自旋向上與向下的差異程度大于B子格。按此理解，BC、BZ和PM的序參量分別是：BC(c=0、d≠0)、BZ(c≠0、d=0)、PM(c=d=0)。

石墨烯原子并不靜止，而是作非簡諧振動。原子靜止時，一個原子平均相互作用能為[15]

(2)

式中的V2為兩原子的sp2軌道σ鍵的共價能，它與原子間距離d的平方成反比

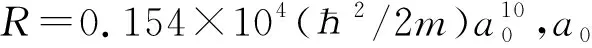
將φ(d)在平衡位置d0附近展開，偏離δ=d-d0很小時，有

(3)

將(2)代入(3)式，求得原子振動的簡諧系數ε0、第一和第二非簡諧系數ε1、ε2，其表示式見文獻[16]。

除石墨烯原子相互作用外，石墨烯電子間也有相互作用，包括：原子間的電子相互作用(稱為原子間的關聯G)、原子內的電子相互作用(稱為內部關聯U)。原子靜止時外延石墨烯電子系統的哈密頓H為基底電子的哈密頓Hs、石墨烯電子的哈密頓Hg和處于第i個格點的石墨烯與基底的電子之間的相互作用哈密頓Hin之和，即

H=Hs+Hg+Hin

(4)

其中，基底為金屬，電子為自由電子，Hs為

(5)

式中的N=NA=NB是基底中電子具有波矢q、自旋為σ=(↑,↓)的態|qσ>的填充數；εs(q)為基底電子波矢q的能量。

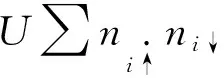
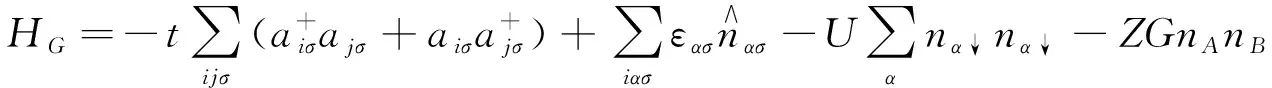
(6)

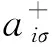
基底與石墨烯的電子之間相互作用哈密頓Hin為

(7)

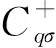
將(5)～(7)式代入(4)式，就得到哈特利一福克近似下，不考慮原子振動時金屬基外延石墨烯電子系統的哈密頓。

2 電子系統的能量

文獻[14]利用格林函數法，求出A、B子格的格林函數，進而求出不考慮原子振動時金屬基外延石墨烯電子系統的能量為

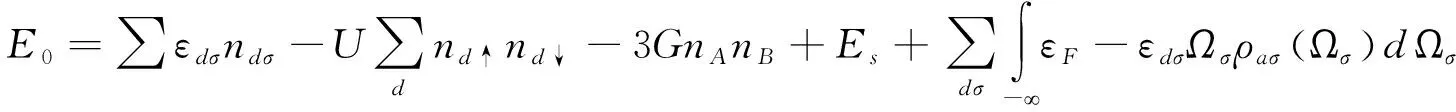
(8)

其中，εF為費米能，εdσ為α子格中自旋為σ的一個電子的能量，nασ為α子格自旋為σ的電子數，nA、nB為A、B原子電子數，Es為基底能量。

ρaσ(Ωσ)為a子格中電子自旋為σ，以Ωσ為變量的態密度。

考慮原子作非簡諧振動后，石墨烯中要產生大量的聲子，電子與聲子之間有相互作用，外延石墨烯電子系統的能量E除E0外，還要加上電子與聲子之間相互作用能ΔEep，即

E=E0+ΔEep

(9)

電子與聲子相互作用能量ΔEep與一個電子與一個聲子相互作用能W成正比外，還與產生的聲子數nq成正比，即ΔEep∝Wnq。按照統計理論，具有能量為?ωq的聲子的數目為

(10)

考慮原子作非簡諧振動后，式中的聲子頻率ωq不是常數，而是與溫度有關：

(11)

這里ω(0)是T=0K時石墨烯原子振動的頻率，它與原子質量M和簡諧系數ε0的關系為：ω(0)=(ε0/M)1/2。還注意到，由于自旋相反的電子與聲子的相互作用會抵消，抵消的結果只有[(nA↑-nA↓)-(nB↑-nB↓)]個電子與聲子有相互作用。用序參量表示后，系統的電子與聲子相互作用能為

(12)

將(12)和(8)式，代入(9)，得到外延石墨烯電子系統的能量為

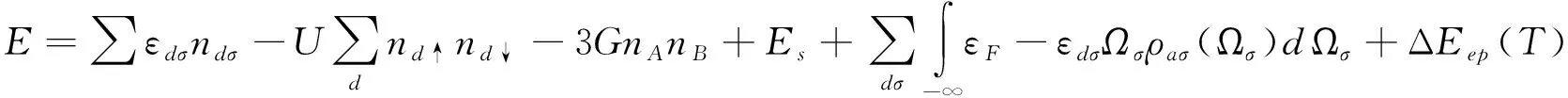
(13)

3 外延石墨烯的相圖

外延石墨烯的磁性和半金屬性等主要由電子系統的自旋狀態決定，序參量a、b、c、d的情況決定了系統處于何種狀態。

3.1 不考慮原子非簡諧振動情況

利用(1)式，將nA、nB以及na↑、nb↑等用序參量a、b、c、d表示。近鄰格點間電子間的交換作用很小，可設t=0。由(13)式，得到外延類石墨烯的能量E與序參量a、b、c、d和溫度T以及U、G等的關系式，即E=E(a,b,c,d,U,G,T)，在a=1，b=0(即一個原胞上有2個電子，磁化強度為零)情況下，外延類石墨烯的BC(c=0、d≠0)態、BZ(c≠0、d=0)態、PM(c=d=0)態電子系統的能量EBC、EBZ、EPM分別為：

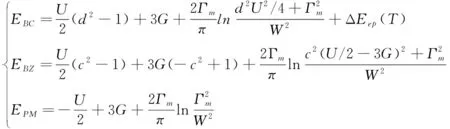
(14)

考慮到原子非簡諧振動主要影響的是G，由EBC=EBZ=EPM，得到三相點的關聯U、G滿足U=πΓm、3G=πΓm+2dΔEep，而序參量滿足：

(15)

分別由EBC=EBZ、EBC=EPM和EBZ=EPM得到鐵磁-抗磁相變曲線1、鐵磁-半金屬相變曲線2和抗磁-半金屬相變曲線3。

不考慮原子非簡諧振動(ΔEep=0)時，由(14)、(15)得到三相點為：U=πΓm、3G=πΓm，序參量c，d滿足：

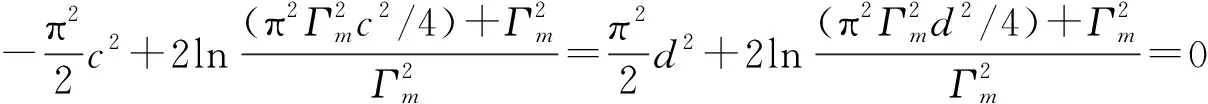
(16)

相變曲線滿足：

(17)

3.2 考慮原子非簡諧振動情況

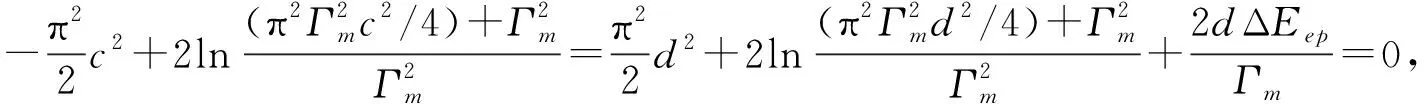
(18)

以U為縱坐標，G為橫坐標，由(17)、(18)就得到外延類石墨烯的相圖。

4 非簡諧振動對外延石墨烯相圖的影響

現以鎢基底上的外延石墨烯為例作討論。文獻[16]已由求得：石墨烯的簡諧系數ε0、第一和第二非簡諧系數ε1、ε2為：ε0=3.5388×102J·m-2、ε1=-3.49725×1012J·m-3、ε2=3.20140×1022J·m-4。C原子的質量M=1.995017×10-26kg，求得ω(0)=(ε0/M)1/2=1.5296×1014s-1，由(11)式求得ωq(T)，一個電子與一個聲子相互作用能W按文獻[17]，W=0.5 eV，代入(12)式，求得ΔEep(T)。

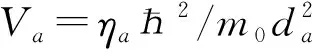
將這些數據代入(17)式，得到不考慮原子振動時外延石墨烯的相圖如圖3。

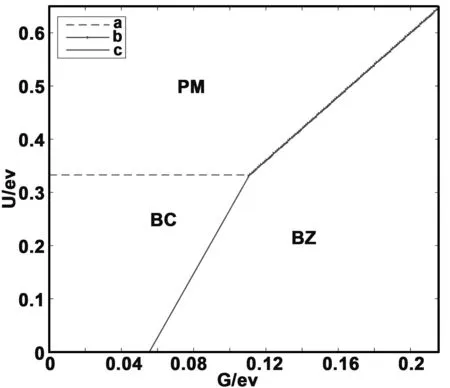
圖3 不考慮原子振動時鎢基底外延石墨烯的相圖Fig 3 Phase diagram of epitaxial graphene on tungsten substrate without considering atomic vibration

由圖3看出：鎢基底外延石墨烯中，會出現半金屬相、反鐵磁相、順磁相這三種狀態，至于出現何種狀態，取決于外延石墨烯中原子內部的電子關聯U和原子間的電子關聯G。只有在原子內部的電子關聯U和原子間的電子關聯G分別為U=0.33284 eV和G=0.11904 eV時，才會出現半金屬相、反鐵磁相、順磁相這三相共存。

將ΔEep(T)和上述這些數據代入(18)式，得到溫度T=300 K時，考慮原子振動時外延石墨烯的相圖如圖4，圖中線0、1、2分別為簡諧近似、計算到第一非簡諧和同時計算到第一、二非簡諧項的結果。

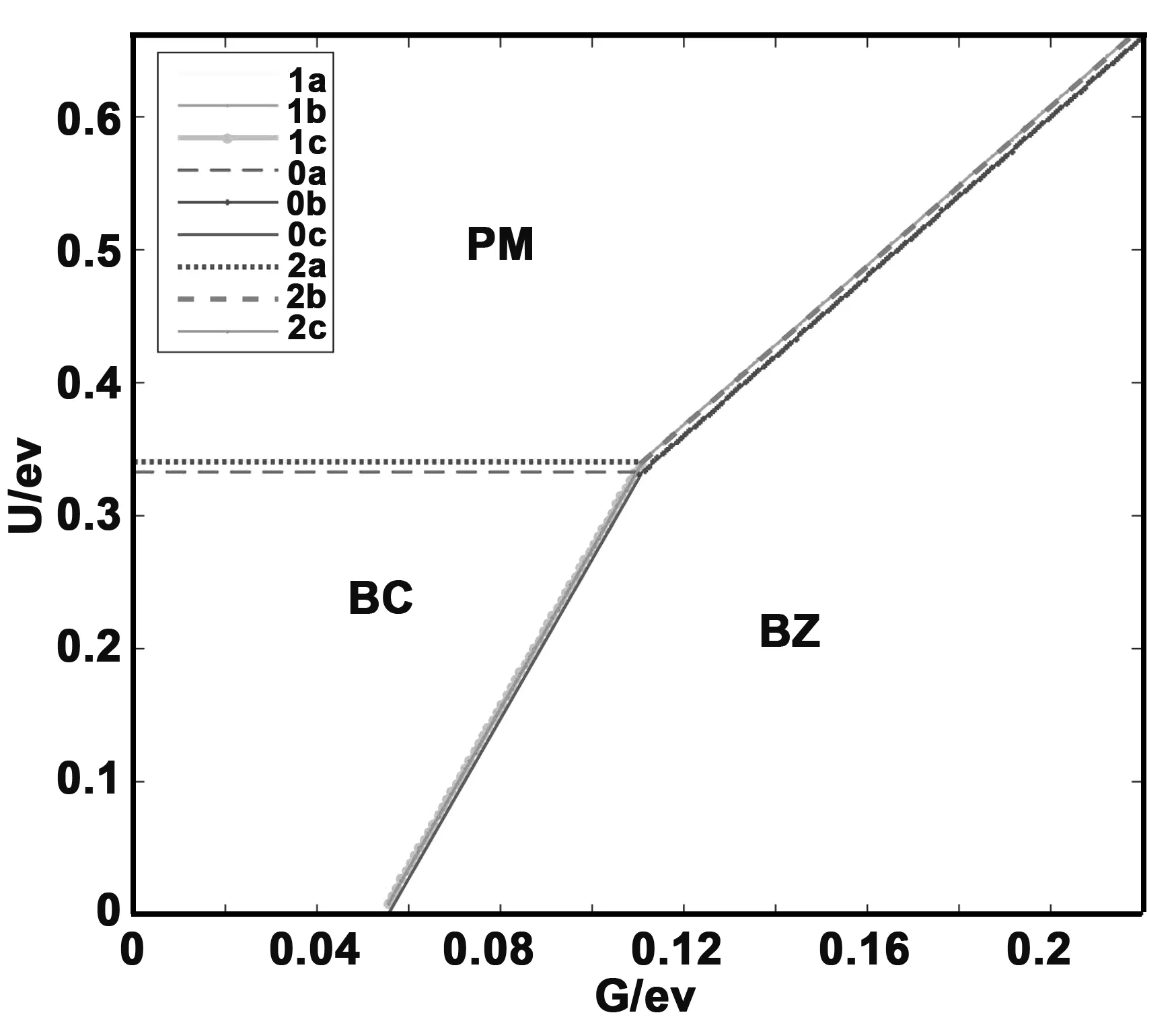
圖4 考慮原子非簡諧振動時外延石墨烯的相圖Fig 4 Phase diagram of epitaxial graphene considering atomic anharmonic vibration

由圖3和4看出：不考慮原子作非簡諧振動時，外延石墨烯的相圖與溫度無關，即系統的鐵磁-抗磁-半金屬相變取決于原子內部的電子關聯U和原子間的電子關聯G，而考慮原子作非簡諧振動時，外延石墨烯的鐵磁—抗磁—半金屬相變還與溫度有關：在相同的原子間的電子關聯G情況下，考慮原子作非簡諧振動后，原子內部的電子關聯U要比原子靜止時的U增大(即原子內部的電子之間相互作用增強)時，才會發生半金屬-反鐵磁-順磁相變。即：考慮原子作非簡諧振動后，發生半金屬-反鐵磁-順磁相變的條件對原子內部的電子之間相互作用要更強。溫度愈高，非簡諧效應愈突出，金屬基單層外延石墨烯中發生半金屬-反鐵磁-順磁相變的條件愈高，發生相變就更不容易。也就是說，低溫下該材料中更易發生半金屬—反鐵磁—順磁相變。

5 結 論

對金屬基單層外延石墨烯的相圖的變化規律進行研究，結果表明：(1)考慮到原子的非簡諧振動后，金屬基外延石墨烯也有自旋態密波(BC)、電荷密度波(BZ)和半金屬態(PM)這三種狀態，它們的相圖和相平衡線不僅與石墨烯電子的直接和間接庫侖排斥能U和G有關，而且還與溫度等有關，具體關系由(17)和(18)式決定；(2)金屬基單層外延石墨烯出現半金屬、反鐵磁、順磁這3種相中何種狀態，取決于外延石墨烯中的電子關聯U和G。只有當U=0.33284 eV和G=0.11904 eV時，才會出現半金屬相、反鐵磁相、順磁相這三相共存；(3)原子的非簡諧振動對金屬外延石墨烯的相圖有重要影響：在相同原子間的電子關聯G情況下，使發生半金屬—反鐵磁—順磁相變對原子內部的電子之間相互作用要更強。不考慮原子作非簡諧振動時，外延石墨烯的相變與溫度無關。考慮原子的非簡諧振動后，外延石墨烯的相變與溫度有關，在低溫時發生半金屬—反鐵磁—順磁相變更容易。