基于改進CV模型模擬超快激光加熱過程
毛煜東呂慧麗孫浩森楊開敏于明志
(山東建筑大學 熱能工程學院,山東 濟南250101)
0 引言
超快激光加熱技術具備高精確性和精細性的特點,已廣泛應用于激光焊接[1]、激光鉆孔[2]、激光清洗[3-4]、激光圖案化[5-6]、激光打標[7-8]、激光淬火[9-10]以及激光沉積[11-12]等諸多領域,在微/納米薄膜和器件的加工中、制作精細的醫療設備和醫療手術等領域也贏得了一席之地。隨著激光技術需求的擴大,對超快激光加熱技術熱傳遞現象的研究也變得十分重要。
傅里葉經試驗研究提出了用于描述宏觀導熱過程的傅里葉定律。目前,通常使用的基于傅里葉定律的擴散理論對設備中的熱傳輸建模,已廣泛地應用到機械、冶金、建筑以及電氣等領域,現也應用到超快激光加熱問題中[13]。然而,在介質傳熱中應用傅里葉定律時,表現出無限的傳輸速度。這是由于傅里葉試驗過程中假設熱載子之間經過多次碰撞達到熱平衡,熱流密度矢量和溫度梯度矢量之間不存在時間差,這使得傅里葉定律暗含了熱擾動的傳播速度為無限大。對于超快速熱傳導問題,溫度會在極短時間和微小空間內發生劇烈變化,邊界處也會產生超高的溫度梯度。對于超快速激光加熱過程,其特征尺度已經到了納米/微米級,甚至更小,而且超快速激光加熱的熱作用時間大多在ps(10-12s)和fs(10-15s)量級,因此研究超快速激光加熱過程中的非傅里葉現象具有重要意義。
Cattaneo對傳統的傅里葉定律進行了修正,提出了著名的非傅里葉導熱模型,也稱之為CV 模型[14]。Alvarez等[15]為了描述熱傳輸從擴散狀態到彈道狀態的過渡,討論了包括記憶和非局部效應的廣義傳輸模型,并隨后研究了從擴散到彈道狀態的一些納米系統的尺寸和頻率依賴性,提出了改進的CV導熱模型(以下簡稱改進模型),其反映了微尺度熱傳導的記憶效應和尺寸效應[16]。文章利用改進模型和CV模型分別模擬了絕熱條件下超快激光誘導金薄膜的一維溫度分布,并對其結果進行了比較分析。
1 理論分析
1.1 應用CV模型模擬超快激光加熱金薄膜過程
Cattaneo提出的CV模型可由式(1)表示為
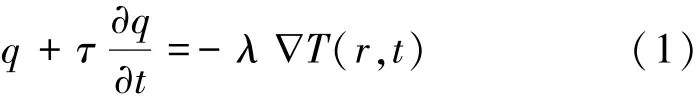
式中:r為位置矢量;t為時間變量;q為熱流密度矢量;λ為材料的導熱系數;?T(r,t)為溫度梯度;τ為系統中連續介質熱通量的相位滯后,是介質的固有熱特性。
考慮在由超快激光加熱的金薄膜中的一維熱傳播中,基于CV導熱模型的溫度控制方程由式(2)表示為
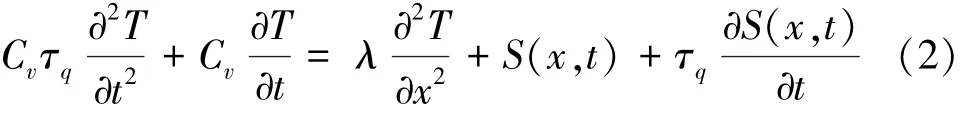
定解條件由式(3)和(4)表示為
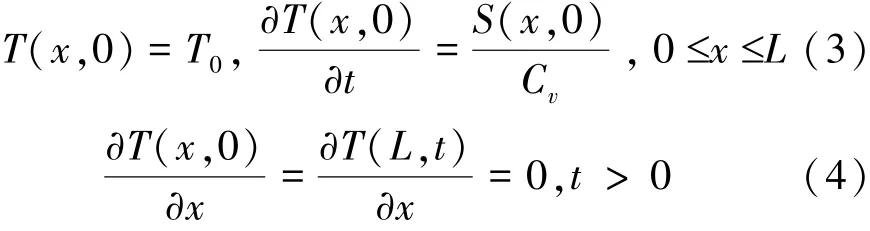
式中:Cv為定容比熱容;L為金薄膜厚度;x為位置參數;τq為金薄膜中熱載子的弛豫時間;S(x,t)為激光能量密度表達式,可由式(5)[17]表示為
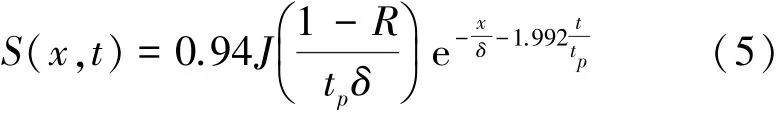
式中:J為激光能量發射密度;R為表面反射率;tp為激光脈沖的持續時間;δ為激光穿透深度。
對方程(2)~(4)進行無量綱化,令
則溫度控制方程和定解條件由式(7)~(9)表示為
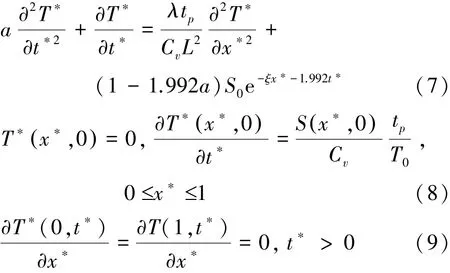
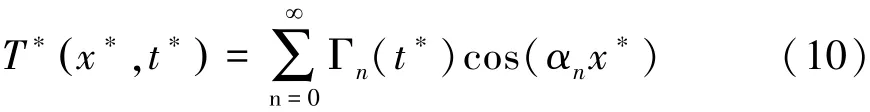
式中:αn =nπ(n=1,2,3,…)。將式(10)帶入控制方程(6)并利用余弦函數cos(αnx?)的正交性可得式(11)為
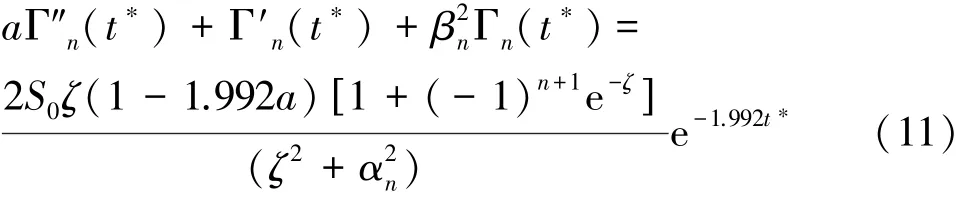
(1)當Δ>0時,
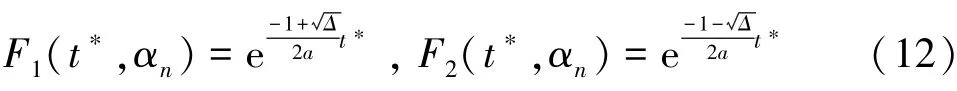
(2)當Δ<0時,
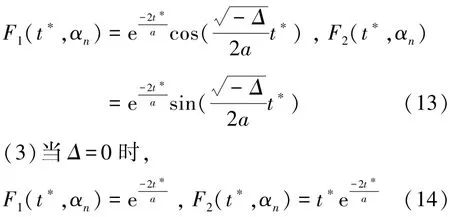
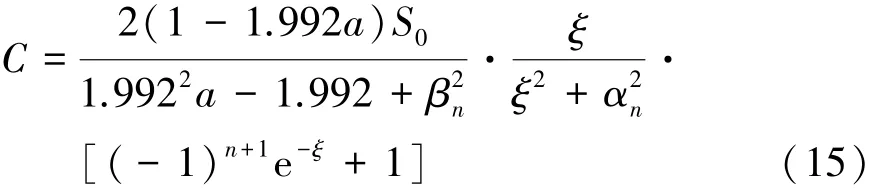
因此,方程(7)的解可由式(16)表示為
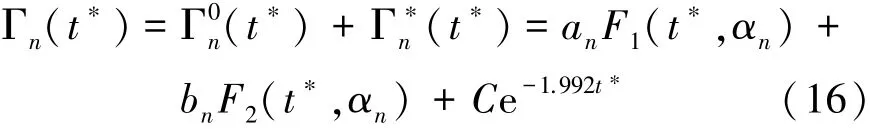
利用初始條件(8)和余弦函數正交性,由式(17)和(18)表示為
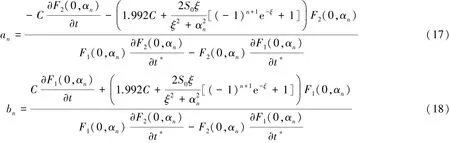
首項Γ0(t?)滿足方程(19)為
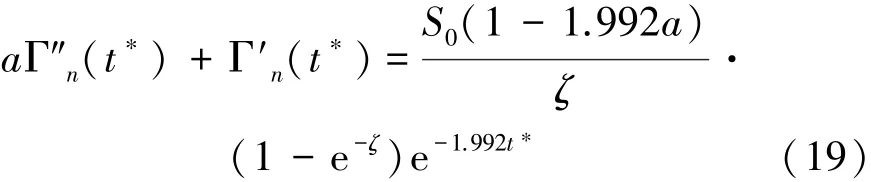
求解方程(19)得式(20)為
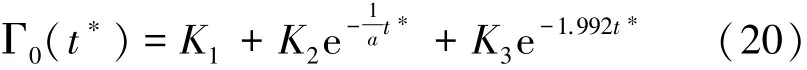
其中,K1、K2和K3分別由式(21)~(23)表示為
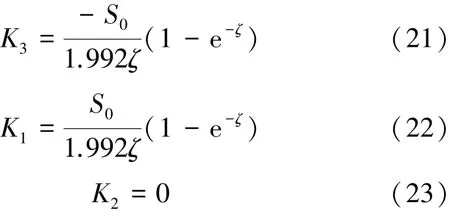
則定解問題(7)~(9)的解由式(24)表示為
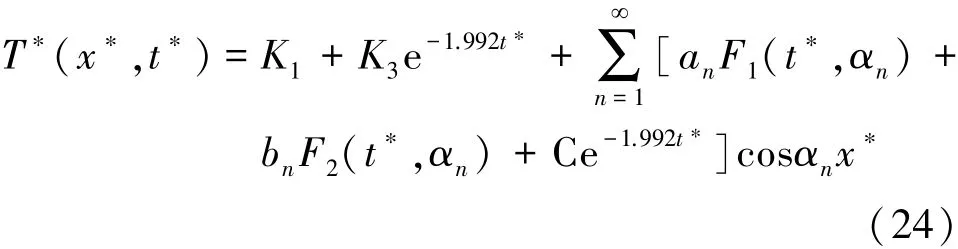
式中:K1、K3、an、bn、C均為替代參數。
1.2 應用改進CV模型模擬超快激光加熱金薄膜過程
Alvarez等[15]提出的改進的CV模型可用式(25)表示為
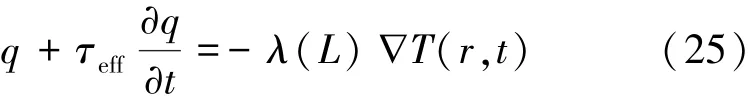
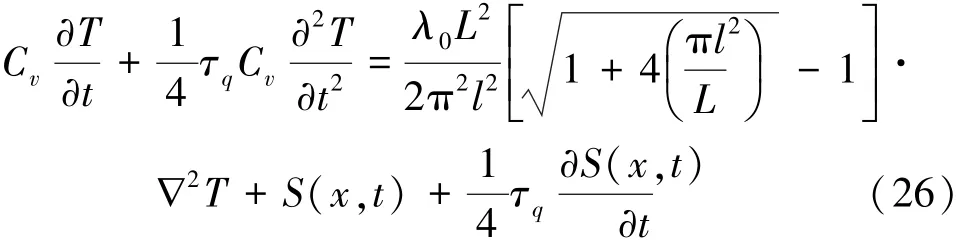
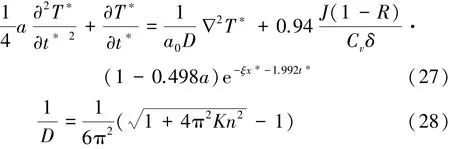
式中:D為替代參數在應用改進模型時考慮的邊界條件和初始條件。應用1.1節中介紹的方法,最終得到基于改進模型的無量綱溫度的解由式(29)表示為
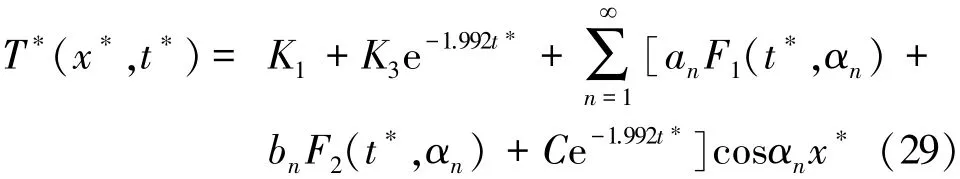
(1)當Δ>0時,
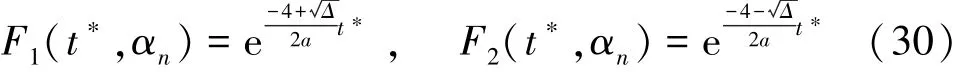
(2)當Δ<0時,
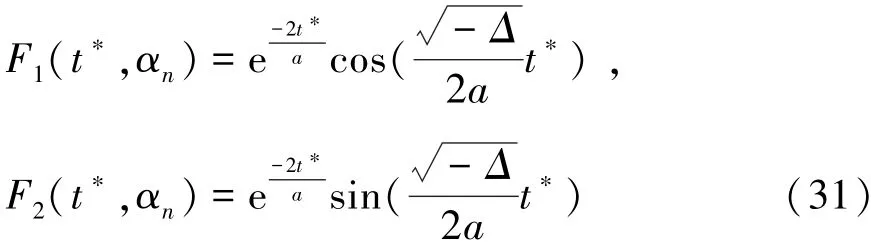
(3)當Δ=0時,
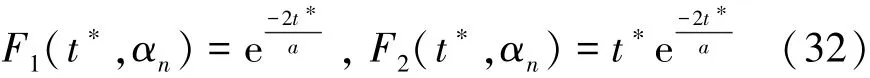
方程(29)中的其他未知參數可分別由式(33)~(35)表示為
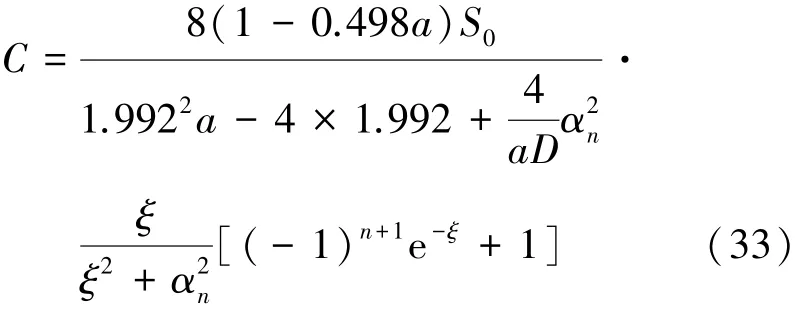
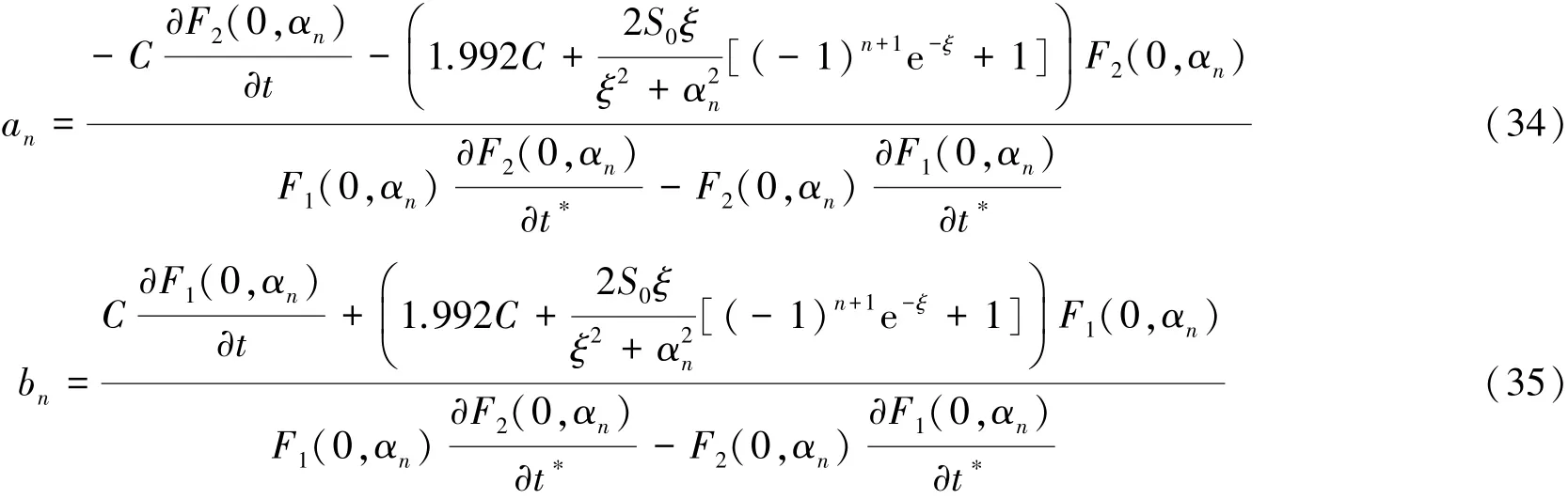
2 數值模擬結果與分析
考慮用超快脈沖激光加熱金薄膜。金薄膜的定容比熱容Cv為2.5×106J/(m3·K),薄膜由650 fs(tp=0.65 ps)激光加熱,且金薄膜中熱載子的弛豫時間τq為6.5 ps。激光能量密度J為732 J/m2,激光穿透深度δ為15.3 nm,金薄膜的特征長度L為410 nm,激光的表面反射率R為0.93。
2.1 改進CV模型加熱金薄膜的結果分析
改進模型所獲得的結果如圖1所示。(1)選取克努森數為0.1的金薄膜,基于體現尺度效應和遲滯效應的改進模型得到的薄膜內部無量綱溫度在不同時刻下的變化情況如圖1(a)所示,在t?=0.2時刻,受激光脈沖加熱的左側無量綱溫度為180(即實際溫度480 K)。(2)左側溫度迅速升高,當t?=1時,薄膜左側無量綱溫度達到最高值約為471(實際溫度771 K)。隨著時間的推移,薄膜左側溫度逐漸下降,熱量自左向右傳遞,薄膜右側的溫度逐漸升高,但溫度的峰值點始終位于受加熱的左端。當克努森數增大到0.5時,如圖1(b)所示,發現由改進模型得到的溫度分布中,靠近薄膜左側區域的溫度僅僅略低于薄膜左壁的溫度,也就是說,薄膜內的溫度從左到右先緩慢下降一段區域后又迅速下降,且隨著時間的推移,薄膜內溫度的緩慢下降的區域增大。這也是一種波動的傳播方式,但注意到溫度波峰始終處于薄膜左端。當經歷足夠長時間(在此選取t?=100)后,薄膜內溫度達到穩定狀態,溫度分布呈一條水平線。圖1(c)和(d)分別表示了克努森數為1和2的情況,所反映出來的熱傳遞過程與克努森數等于0.5展示的情況類似。在改進模型中,熱波傳播速度可表示為。通過對比圖1(a)~(d)還發現,隨著克努森數的增加,溫度變高,薄膜內溫度達到穩定狀態所需的時間越短。克努森數的增加意味著膜的特征長度減小,因此,溫度場可以迅速達到穩態。
2.2 兩種模型的對比分析
改進模型和CV模型獲得的比較結果如圖2所示,改進模型在受熱處一側的溫度要高于CV模型的結果。如圖2(d)所示,改進模型在受熱側獲得的無量綱溫度為510,但CV模型獲得的則為465。此外,改進模型的熱波速度與CV 模型的熱波速度也不相同。當Kn=0.5時,改進模型獲得的c1值為0.0394,CV模型得到的結果為0.0289。但是,當Kn=2時,改進的CV模型獲得的c1的值等于0.0885,而CV模型得到的結果為1.156。令c1=c,得到克努森數等于1.1027。因此,當Kn<1.1027時,改進模型得到的熱波速度大于CV模型得到的熱波速度,而當Kn>1.1027時,改進模型得到的熱波速度小于CV模型得到的結果。需要強調的是,對于超快激光加熱納米尺度薄膜的一維導熱過程,這兩個模型都展示了在薄膜內部熱是以波動的方式進行輸運的,而不再是傅里葉定律給出的熱的擴散傳遞形式,說明在薄膜內熱量是以有限速度進行傳輸的。
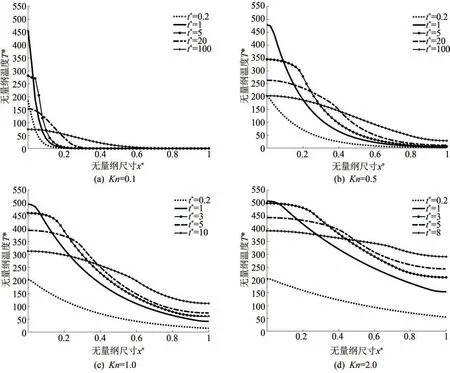
圖1 改進模型得到的不同克努森數在不同時刻t?下的溫度分布圖
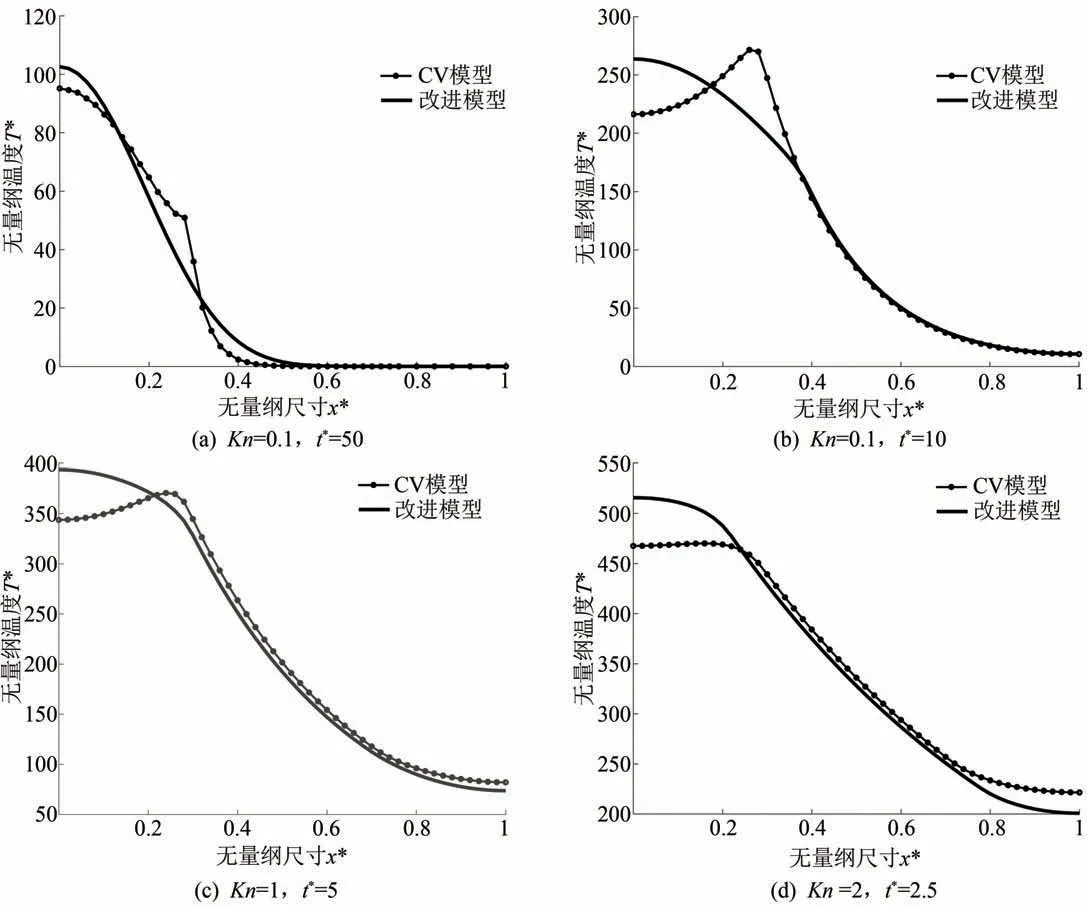
圖2 改進模型和CV模型得到的無量綱溫度分布圖
3 結論
文章基于體現尺度效應和遲滯效應的改進模型研究了超快脈沖激光加熱薄膜的一維導熱過程,對其結果進行了分析,并同CV模型所得的結果進行了比較,主要得到以下結論:
(1)改進模型展示出受熱處溫度迅速升高且峰值要高于CV模型的結果,能量是以波的形式傳遞到另一端;隨著克努森數的增加,溫度變高,薄膜內溫度達到穩定狀態所需的時間越短。
(2)兩個模型所得無量綱速度值的大小關系會隨著克努森數的值的變化發生改變,當Kn<1.1027時,改進模型的熱波速度要高于CV模型的熱波速度;當Kn=1.1027時,改進模型的熱波速度等于CV模型的熱波速度;Kn>1.1027時,改進的CV 模型的熱波速度要小于CV模型的熱波速度。
(3)改進模型不僅是模擬超快脈沖激光加熱薄膜問題的有效方法,還可以反映尺寸效應和記憶效應,從而可以描述有限熱波傳播速度對傳熱的影響。

