直線與圓的位置關系中的二變元問題的最大值問題探析

莊 順

(福建省廈門第六中學 361000)

在近年的高考題、自主招生題、競賽題或模擬題中，經常會有求解涉及雙變元或多變元問題中的最值或取值范圍問題．此類問題由于變元較多，切入點沒有太大規律，往往導致難度較大，且比較難加以突破．也正是由于變元較多，此類問題破解的思維方式多變，切入點眾多，方法有時也多樣．

【高考真題】(2018·北京理·7)在平面直角坐標系中，記d為點P(cosθ，sinθ)到直線x-my-2=0的距離．當θ，m變化時，d的最大值為( ).

A．1 B．2 C．3 D．4

思維角度1：三角函數法

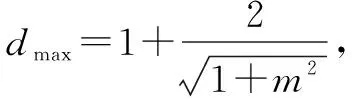
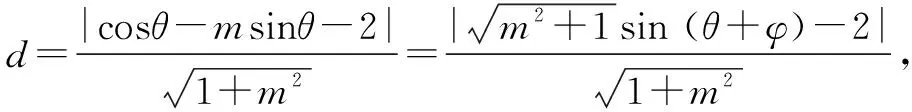
點評把點到直線的距離問題轉化為含有二元函數θ、m的最值問題，分別結合三角函數、二次函數的性質，依次來轉化，進而得以確定相應的最值問題．在這里的解決關鍵是對二元函數θ、m沒有直接關系的條件下，分別有針對性地處理，從而得以轉化與應用．

思維角度2：數形結合法

分析根據題條件確定點P的軌跡與直線恒過定點A(2，0)的性質，先讓直線x-my-2=0保持“靜止”時確定點P到直線的距離的最大值問題，再進一步讓直線x-my-2=0進行“轉動”，通過數形結合來確定最值即可．

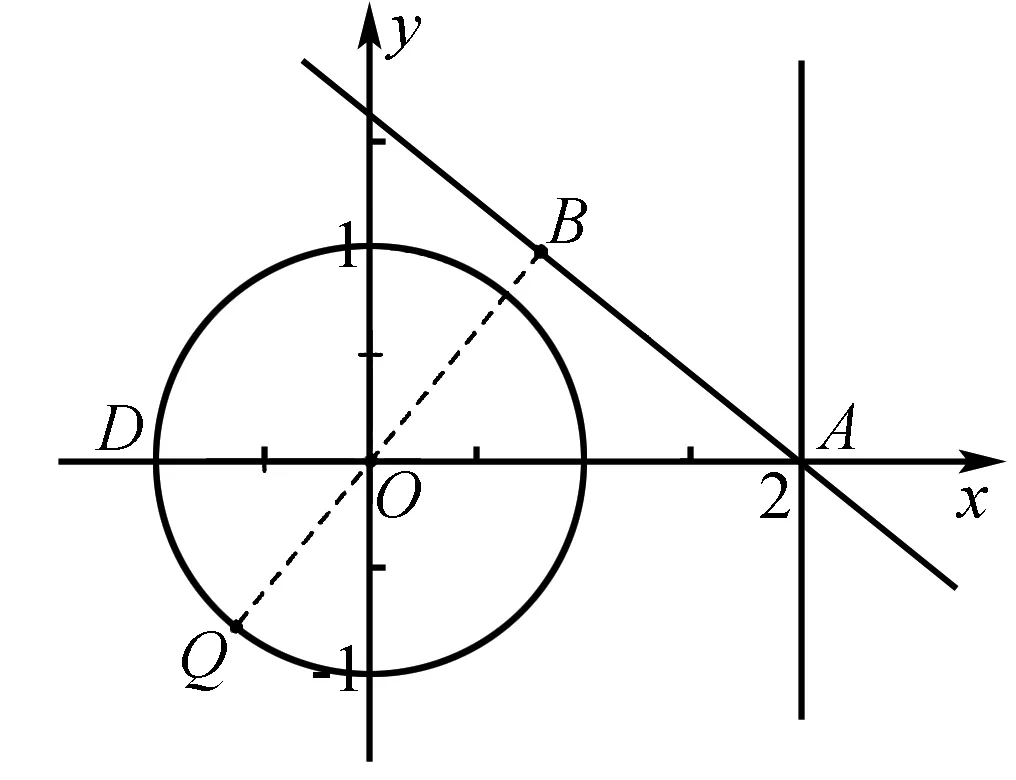
解法2 由于點P(cosθ，sinθ)，則知點P的軌跡是單位圓O：x2+y2=1，而直線x-my-2=0恒過定點A(2，0)的動直線，如圖所示.先讓直線x-my-2=0保持“靜止”，過O垂直于直線x-my-2=0的直線交單位圓O：x2+y2=1于點Q，交直線x-my-2=0于點B，而單位圓O：x2+y2=1與x軸的負半軸交于點D.根據平面幾何知識可知點P到直線x-my-2=0的距離的最大值為點Q到直線x-my-2=0的距離1+|OB|，接下來，再讓直線x-my-2=0進行“轉動”，數形結合可知1+|OB|≤1+|OA|，所以當點B與點A重合，點Q與點D重合時，1+|OB|的最大值為3.所以當直線x-my-2=0的方程為x=2(此時m=0)，且點P為點D(-1，0)時，d的最大值為|AD|=3.故選擇答案C．

點評根據單位圓與過定點的直線束之間的關系，依次在保持直線“靜止”時讓點P在單位圓上運動，再讓直線“轉動”起來，通過數形結合并利用平面幾何的知識來轉化與應用，進而數形結合得以確定相應的二元問題的最值．

其實，當我們破解完一道數學問題后，要加以不斷總結，不斷領悟反思，進而可以有效達到多角度切入，并能有效進行深度挖掘，進行有效深度學習，從而真正達到觸類旁通、一題多解的效果，有助于培養數學科學的思維習慣，良好的核心素養以及能力素質．