CFD中統計誤差的數值精度分析
閔耀兵,馬燕凱,李松
中國空氣動力研究與發展中心,綿陽 621000
計算流體力學(CFD)是一門利用數值方法模擬流動問題的科學,其所依賴的數值方法在理論設計時需滿足一定的精度要求,而理論設計的精度在CFD應用中不一定能夠達到,因此經常需要對算法的理論設計精度進行數值驗證[1-6]。算法精度的數值驗證過程多以加密網格的方式進行,即通過逐步加密網格,使得數值誤差逐漸減小,由網格加密前后數值誤差的比值和網格尺度的比值可以計算出算法的數值精度[1-6]。一般情況下,相比于選取某固定點的數值誤差而言,對整個計算域內的數值誤差進行統計賦范更具有代表性和普適性。通常情況下,數值誤差的統計方式一般可取其L1范數、L2范數和L∞范數,并認為統計誤差的各范數在描述算法的數值精度上具有等價性。因此,在CFD中對算法進行數值精度驗證時,有些研究人員僅考察統計誤差的L1范數[6-7]或者L2范數[8-10],也有同時考察L1范數和L∞范數的[4-5]以及同時考察L2范數和L∞范數的[11],當然也有更為嚴謹的研究者同時基于L1范數、L2范數和L∞范數等3種常用范數進行數值精度分析的[1-2,12],卻鮮有文獻僅參考L∞范數。
然而,在對某具體的CFD算法的理論設計精度進行數值驗證時,由于CFD算法的理論設計多基于光滑流場假設,在遭遇流場間斷(如激波和接觸間斷等)[8]、網格不連續(如拐折和突然拉伸等)[12-13]等問題時,算法的數值精度可能會存在不同程度的降階問題[8,11-13]。即便是在光滑流場中,在極值點附近采用非線性加權插值也可能會產生降階問題[14]。諸如此類的降階問題通常只會出現于計算區域中的某個局部,不會導致整個計算區域的數值精度全部降階[13]。此時統計誤差的各范數在數值精度上一般不再具有等價性,各范數的數值精度與其賦范方式有關,不同賦范方式可能會給出不同的數值精度[13],且一般情況下L1范數的數值精度最高,而L∞范數的數值精度最低,其中的原因和關系本文將給出詳細分析。
針對統計誤差各范數的數值精度不一致的問題[13],本文通過對統計誤差的具體賦范方式進行理論分析,指出:當且僅當整個計算區域內各點的數值精度完全一致時,統計誤差各范數的數值精度才相等,此時統計誤差的各范數在數值精度上具有等價性;而當全場的數值精度不完全一致時,統計誤差的各范數的數值精度并不一致,其具體精度與賦范方式有關,且一般情況下表現為L1范數的數值精度最高,而L∞范數的數值精度最低。本文的理論分析結果很好地解釋了統計誤差各范數的數值精度之間的關系,同時也為CFD算法精度驗證時的誤差統計方式提供了理論參考。
在理論分析的基礎上,本文分別針對全場各點精度不完全一致和完全一致的情形進行了驗證,驗證的結果與理論分析結論相符。然后對極值點附近的非線性加權插值引起的降階問題進行了具體分析,利用本文的理論分析結論,從數值精度上較好地解釋了非線性加權插值在極值點附近的降階問題。
1 統計誤差的數值精度分析
當計算區域中離散的網格尺度為h時,記整個離散區域中誤差統計的總點數為Nh,則隨著計算網格的加密,網格尺度h減小而總點數Nh增大,即Nh與1/h成正變關系。將每個點的數值誤差ei簡單表示為
ei=cihrii=1,2,…,Nh
(1)
式中:ri為第i點的數值精度,一般情況下ri均為整數(?i);ci為與網格尺度h無關的誤差常數,一般可以表示為求解變量及其導數的函數。
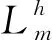
(2)
(3)
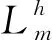
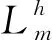
(4)
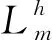
1.1 各點精度不完全一致的情形
在實際CFD計算中,由于離散邊界、流場間斷以及網格不連續等問題的存在,經常會出現各點數值精度ri并不完全相同的情況,即有
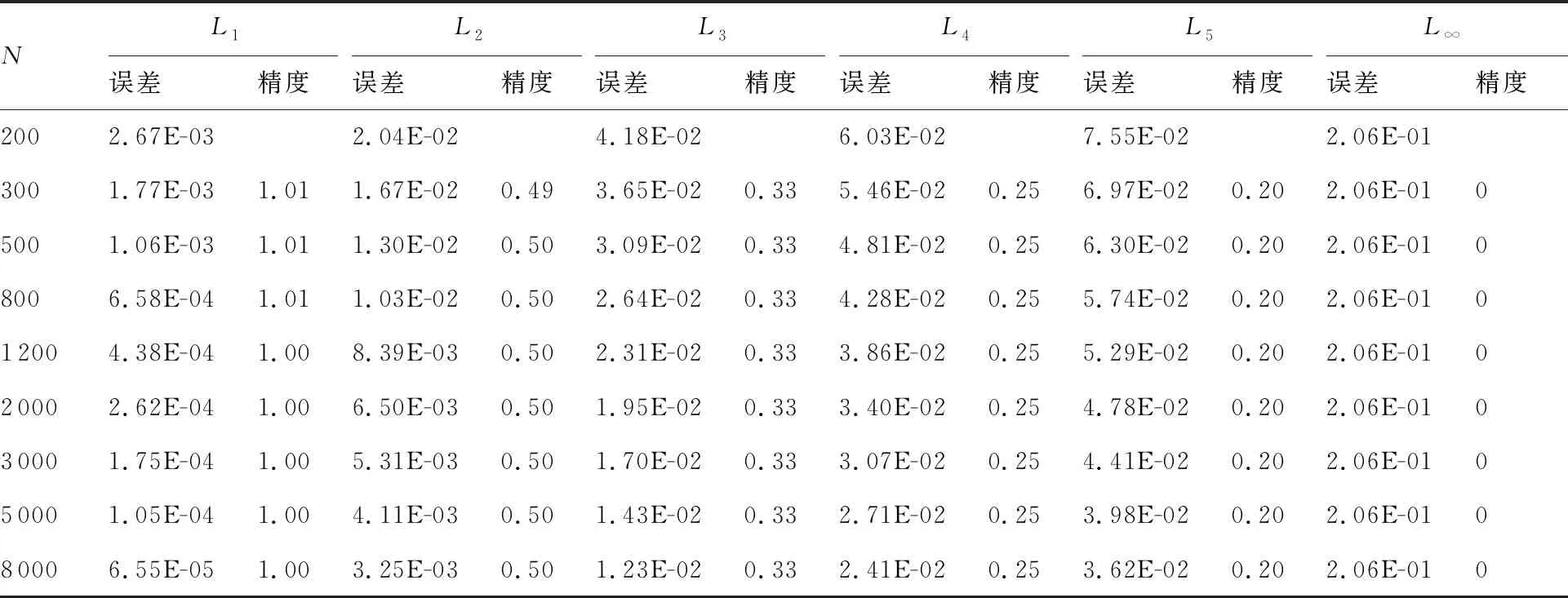
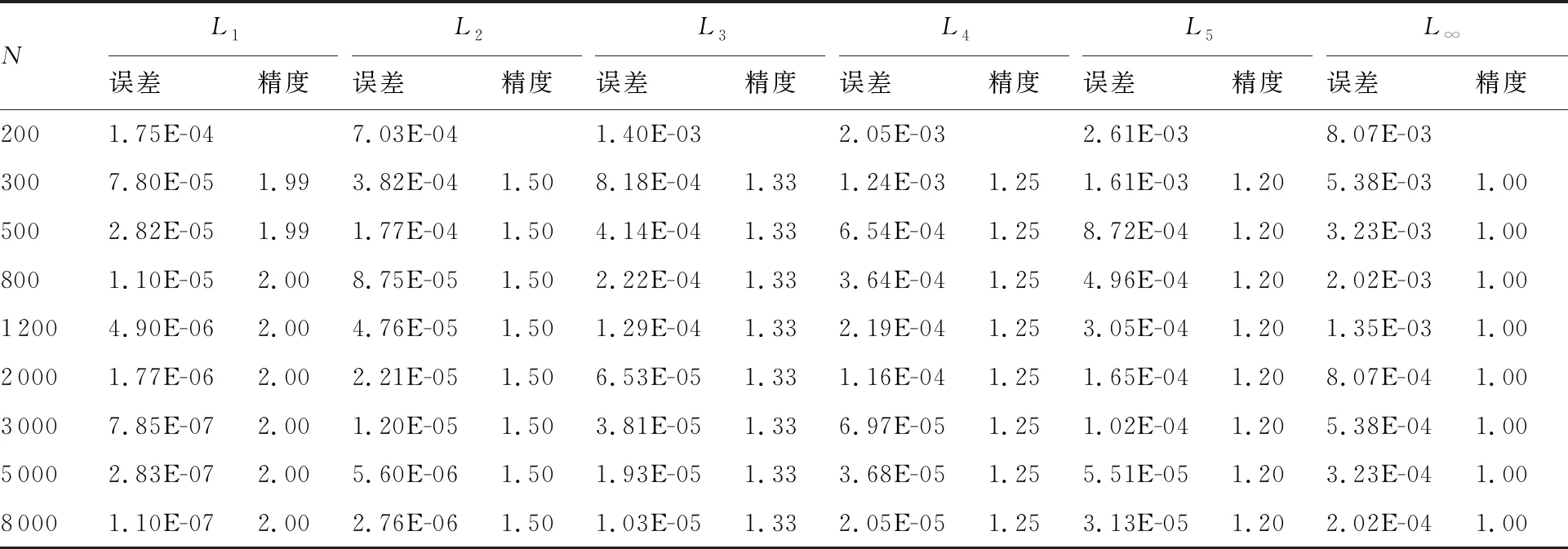
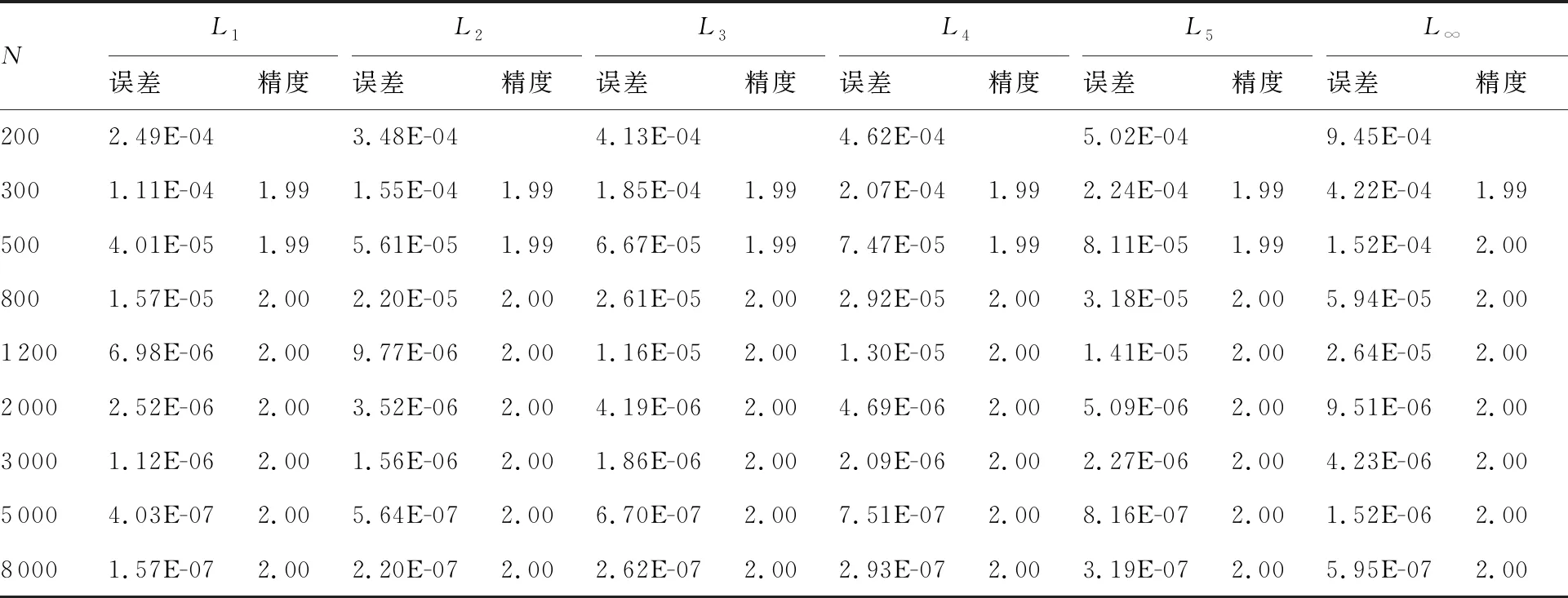
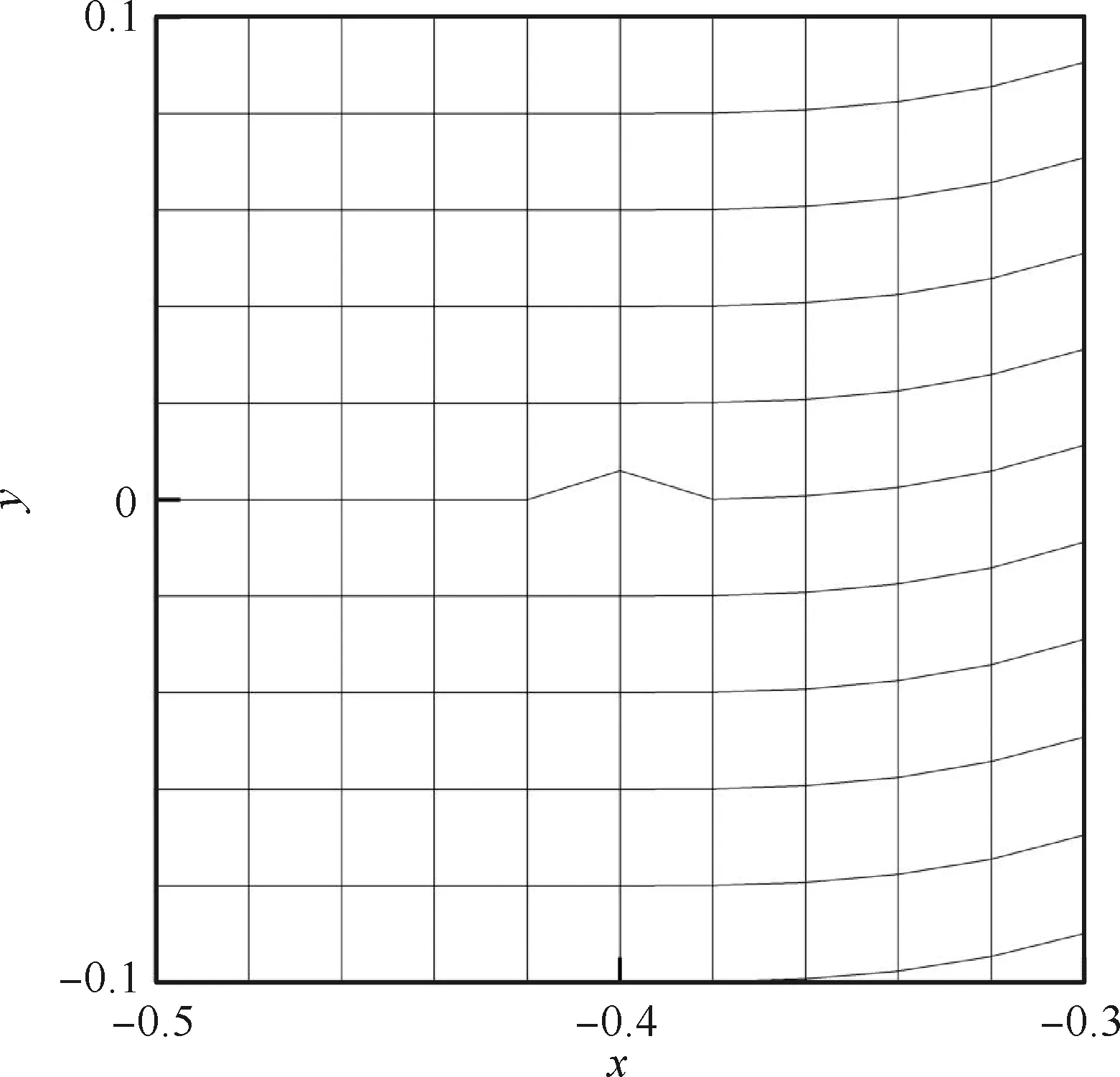
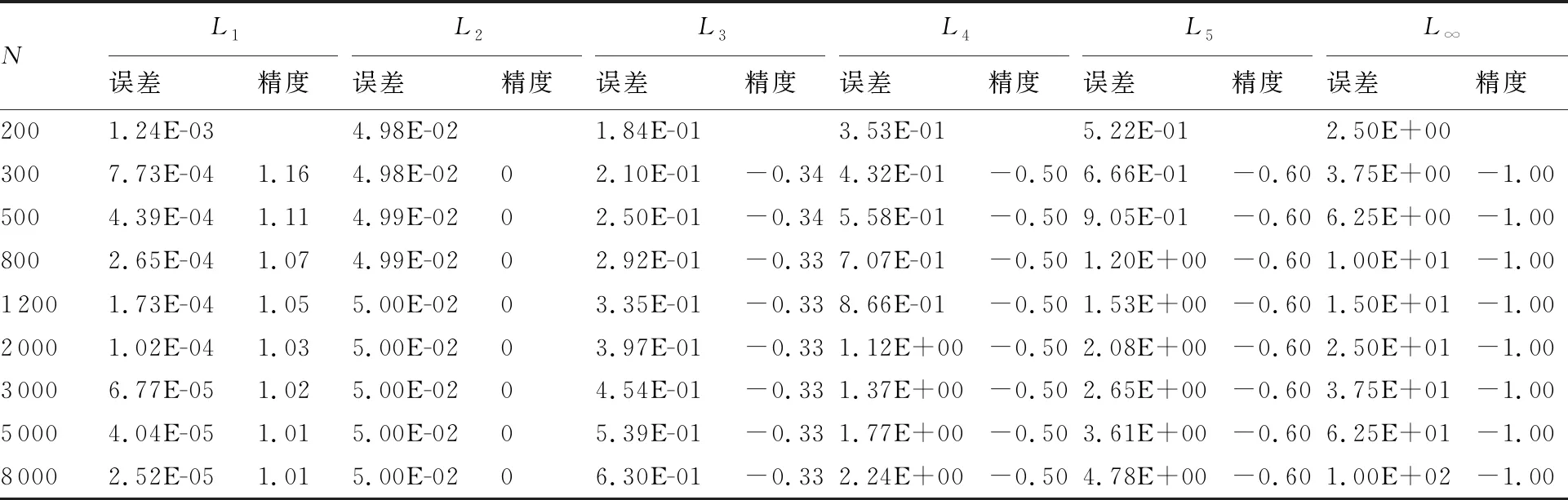
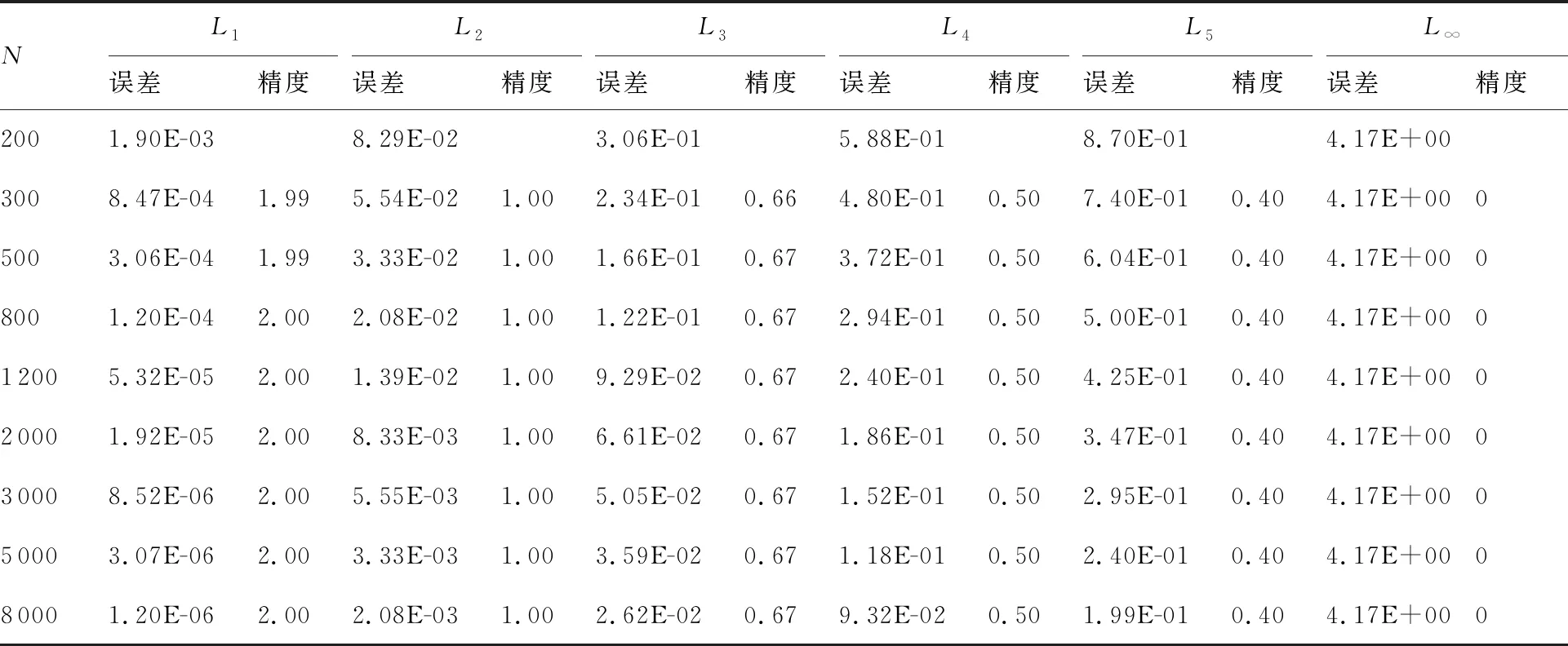
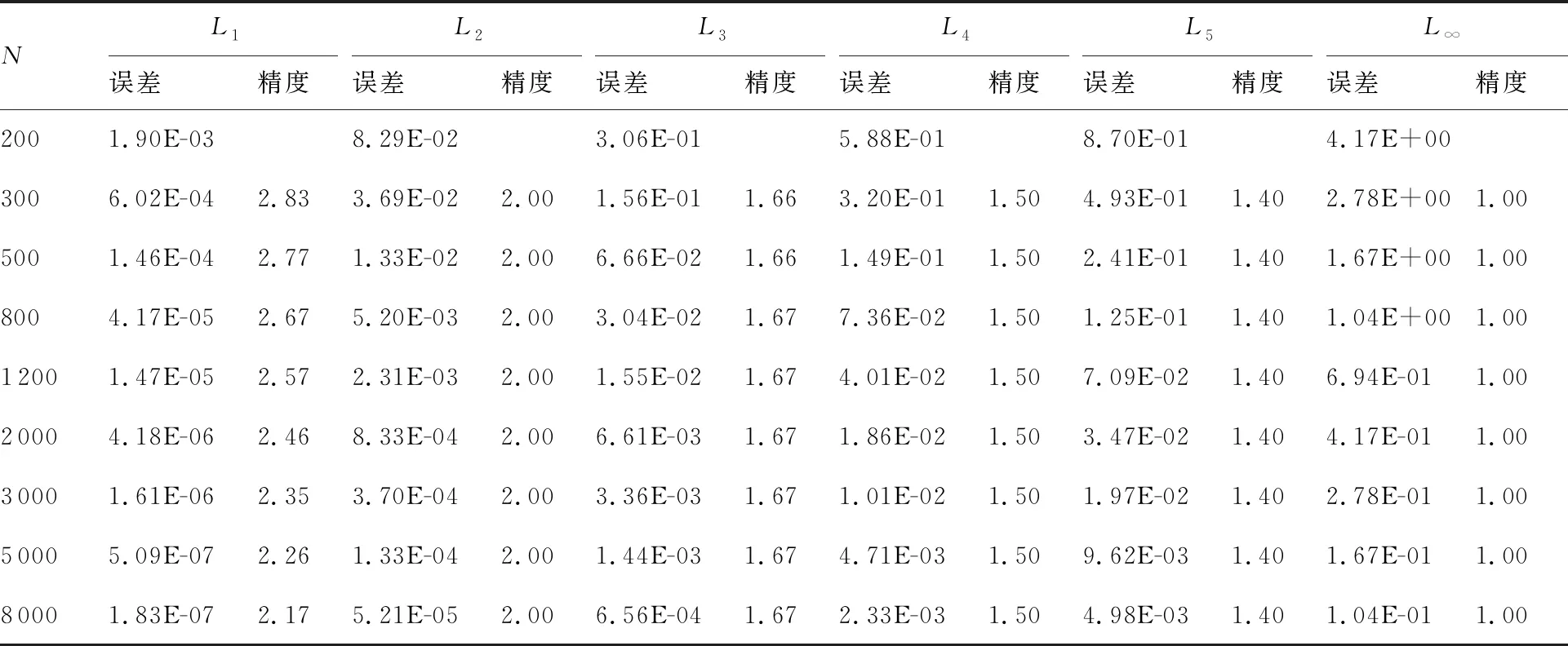
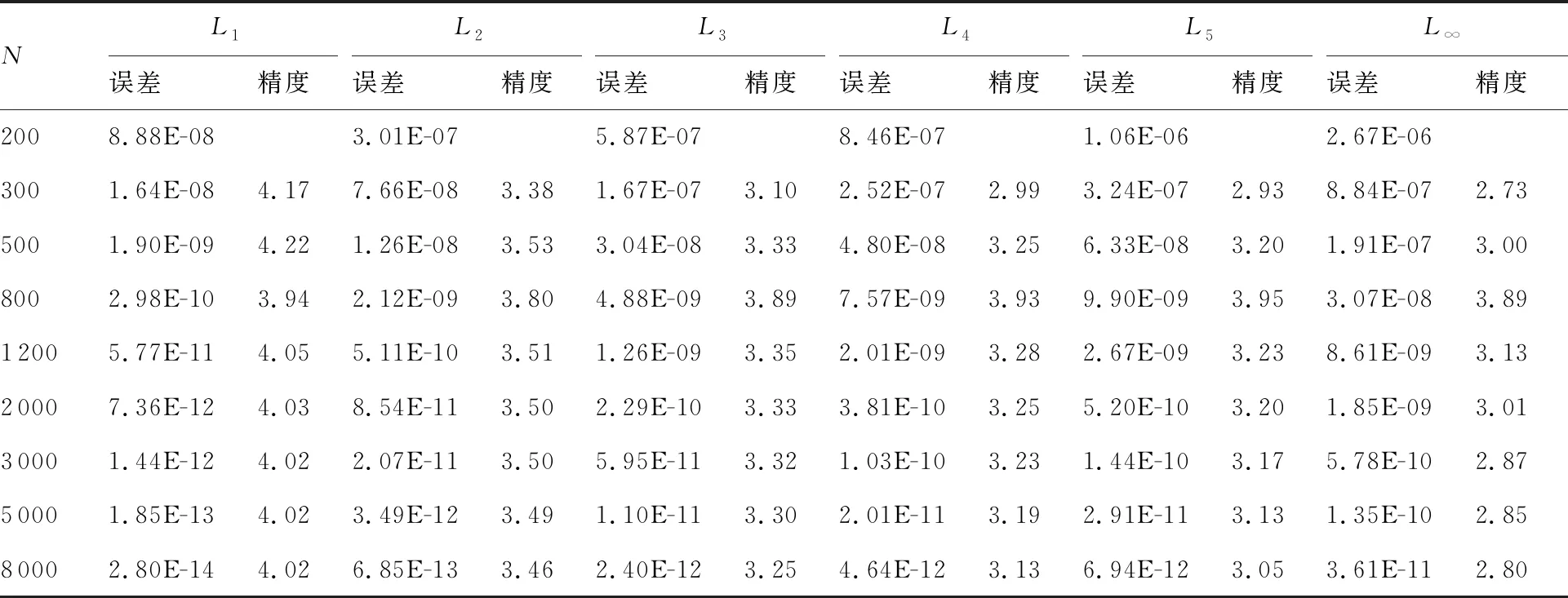
min(ri) (5) 為便于分析,不妨設整個計算區域中總共存在n個數值精度(當各點數值精度不完全相同時,n≥2),其數值由小到大分別記為R1,R2,…,Rn,即 R1=min(ri) (6) 一般情況下,隨著計算網格的加密,精度值Rj以及其數量n均保持不變。不妨記數值精度為Ri的數值誤差的點數為Ni,則有 (7) (8) 不妨記 (9) 由于ci為與網格尺度h無關的常系數,故隨著計算網格的加密,Cj也基本保持不變。由式(9)有 (10) 在網格加密過程中,不妨設網格尺度h的加密倍數rfc為 (11) 式中:下標c和f分別對應粗網格和細網格,網格的加密過程使得rfc>1。當網格尺度加密倍數為rfc時,整個計算區域中誤差統計的總點數Nh的變化關系為 (12) 式中:dN為計算網格的加密維數,dN=1,2,3分別對應一維、二維和三維網格。同時記數值精度為Rj階的誤差點數Nj隨網格的加密滿足: (13) 由于式(7)及Nj dj≤dNj=1,2,…,n (14) 隨著計算網格的加密,誤差統計的總點數Nh要比各精度的點數Nj增加得更快。 根據定義(12)及(13),容易得到 (15) (16) 為便于分析,不妨記 (17) 進一步容易得到 (18) (19) (20) 將式(18)代入(20)中,并整理得到 (21) 由上述分析以及網格尺度關系式(11),容易得到 (22) 由于dN≤3以及式(14),容易知道dj≤3(?j),特別地,對于本文數值算例中考慮的二維問題(dN=2)有dj≤2,又m≥1,則式(22)中的數值精度Om在絕大多數情況下可以表示為 (23) 當m趨于正無窮大時,有 (24) 考慮到一般情況下式(14)及式(23)成立,故有 O1≥O2≥…≥O∞ (25) 即當各點計算精度不完全相同時,其統計誤差L1范數的數值精度O1最高,L2范數的數值精度O2次之,以此類推,L∞范數的數值精度O∞最低。 當全場精度均一致時,有 min(ri)=max(ri)=R (26) 類似于式(8)中的分析,容易得到 (27) 式中: (28) 類似于Cj、Ch也為與網格尺度h無關的常數。此時統計誤差Lm范數的數值精度Om可以表示為 (29) 考慮到網格間距關系式(11)容易得到 Om=R (30) 與各點計算精度不完全相同時的情形不一樣,當各點計算精度均相同時,其統計誤差的各范數均為R階精度,此時統計誤差的各范數之間在數值精度上具有等價性。 針對上述關于統計誤差數值精度的理論分析,設計相應的數值試驗進行驗證。類似于Mao等[13]的做法,設計不同連續程度的網格,計算各點的幾何守恒律誤差并進行誤差統計,通過逐步加密網格以得到統計誤差的各范數的數值精度表現。 本文中采用的周期性二維計算網格基于如下算法解析生成: doj=1,Nj doi=1,Ni if(|x0|<0.4) then y2=sinκ(x2) else y2=0 end if xi,j=x0 yi,j=y0+A·y1·y2 end do end do (31) 式中:Ni和Nj分別為計算坐標下ξ方向和η方向的網格分布點數,實際網格生成過程中取Ni=Nj=N+1;A為波動幅值(A=0時為均勻直角網格),在本文中均取A=0.2;函數y2的指數κ取不同值(在本文中指數κ取1,2,3)時可以得到在x=±0.4處不同連續程度的網格,函數y2描述的網格線如圖1所示。 圖1 函數y2分布 二維網格中幾何守恒律誤差可以表示為(以Ix為例) (32) 式中: (33) (34) 將式(34)的差分算子δ均取為如下的二階精度中心差分格式: (35) (36) (37) (38) 同理有 (39) 而當κ=3時,由于R1=Rn,則由式(26)對應的分析易知 (40) 按照算法(31)生成的網格均滿足d1=1,下面本文考慮另外一種網格中統計誤差的數值精度問題。取κ=3,在算法(31)的基礎上,按照如下方法修正x=±0.4、y=0處的網格分布: 表1 幾何守恒誤差的統計精度(κ=1) 表2 幾何守恒誤差的統計精度(κ=2) 表3 幾何守恒誤差的統計精度(κ=3) if(|x0|=0.4&y0=0) then end if (41) 式中:γ為網格間距指數;B為與網格間距無關的常數,其取值方式為 (42) 式中:參數B的選取使得在x=±0.4、y=0處的網格波動在加密過程中不至于被機器字長所湮沒(雙精度浮點運算)。按照算法(41)生成的計算網格在間斷附近的分布如圖2所示。 圖2 局部網格示意圖(γ=1) 表4 幾何守恒誤差的統計精度(γ=1) (43) (44) (45) (46) 基于算法(41)生成的網格的數值試驗結果見表4~表6。當γ=1和γ=2時,表4和表5中所示的統計誤差的各范數對應的數值精度分別與表達式(44)和式(45)中的完全相同。當γ=3時,表6中給出的統計誤差的各范數的數值精度與理論分析(46)相同,值得注意的是表6中L1范數的數值精度為二階,與理論分析(22)相同,而式(23)此時給出的數值精度應為三階,此時式(22)和式(23)給出的數值精度并不相同。 針對WENO格式的非線性加權插值[4]在極值點附近可能會降階的問題,Henrick等[14]設計了相應的數值算例進行驗證,并指出WENO格式[4]中為避免分母為零而引入的小量ε的取值對數值精度的影響:ε取值相對較大時(如ε=10-6),非線性權近似于其線性最優權,WENO格式在極值點附近一般不會降階;而ε取值較小時(如ε=10-40),非線性權遠遠偏離其線性最優權,WENO格式在極值點附近會存在降階問題。針對目前已得到廣泛應用且同樣采用非線性加權思想構造的WCNS-E-5格式[3,18-19],有必要測試其在極值點附近的數值精度情況[18],為了準確反映WCNS-E-5格式[3]的非線性權在極值點附近的特性,取ε=10-300(四倍精度浮點運算)。 依據算法(31)取A=0生成均勻網格,參照Henrick等[14]的測試方法給定周期性初值: (47) 表5 幾何守恒誤差的統計精度(γ=2) 表6 幾何守恒誤差的統計精度(γ=3) 采用WCNS-E-5格式[3]離散ux并將其相對于解析值的數值誤差統計于表7中,表中的統計誤差的數值精度滿足: (48) 值得指出的是,Henrick等[14]的數值實驗中得出的統計誤差的數值精度與式(48)所述一致,只是Henrick等[14]只給出了m=1,2,∞這3種情況下的精度,且沒有對統計誤差的L1、L2和L∞范數所表現的不同的數值精度給出解釋與說明。 由統計誤差的數值精度式(22)和式(23)易知R1=3,即統計區域中的最低數值精度為三階。對于周期性初值式(47)而言,在極值點附近u′=0、u″≠0、u?≠0,Henrick等[14]的分析指出此時非線性加權的WENO格式只有三階精度,則采用類似非線性加權方式構造的WCNS格式在此類極值點附近也應僅具有三階精度[18],與表7中的最低數值精度為三階相吻合。 由于本算例基于二維網格,故dN=2,由式(22)易知d1=1,即在極值點附近WCNS格式[3]的降階以條帶狀形式出現,條帶的寬度與格式的計算模板有關,但條帶寬度不影響統計誤差的數值精度。 表7 統計誤差的數值精度 針對數值誤差統計時采用的不同賦范方式可能表現出不同數值精度的問題,從理論上詳細分析了統計誤差賦范方式對其數值精度的影響,并給出了一般規律:當且僅當整個計算區域內的數值精度完全一致時,統計誤差各范數的數值精度才相等,此時統計誤差的各范數在數值精度上才具有等價性;而當全場的數值精度不完全一致時,統計誤差各范數的數值精度并不一致,其具體精度與賦范方式有關,且一般情況下表現為L1范數的數值精度最高,L2范數的數值精度次之,以此類推,L∞范數的數值精度最低。 基于統計誤差數值精度的理論分析結論,本文有針對性地設計了相應的數值試驗予以驗證,對于全場精度完全一致和不完全一致的情況,數值試驗均給出了與理論分析完全吻合的結果,表明本文的研究結論能夠為CFD中算法的精度驗證提供理論依據。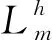
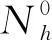
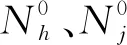
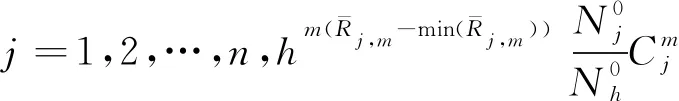
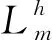
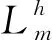
1.2 各點精度一致的情形
2 數值算例
2.1 網格生成
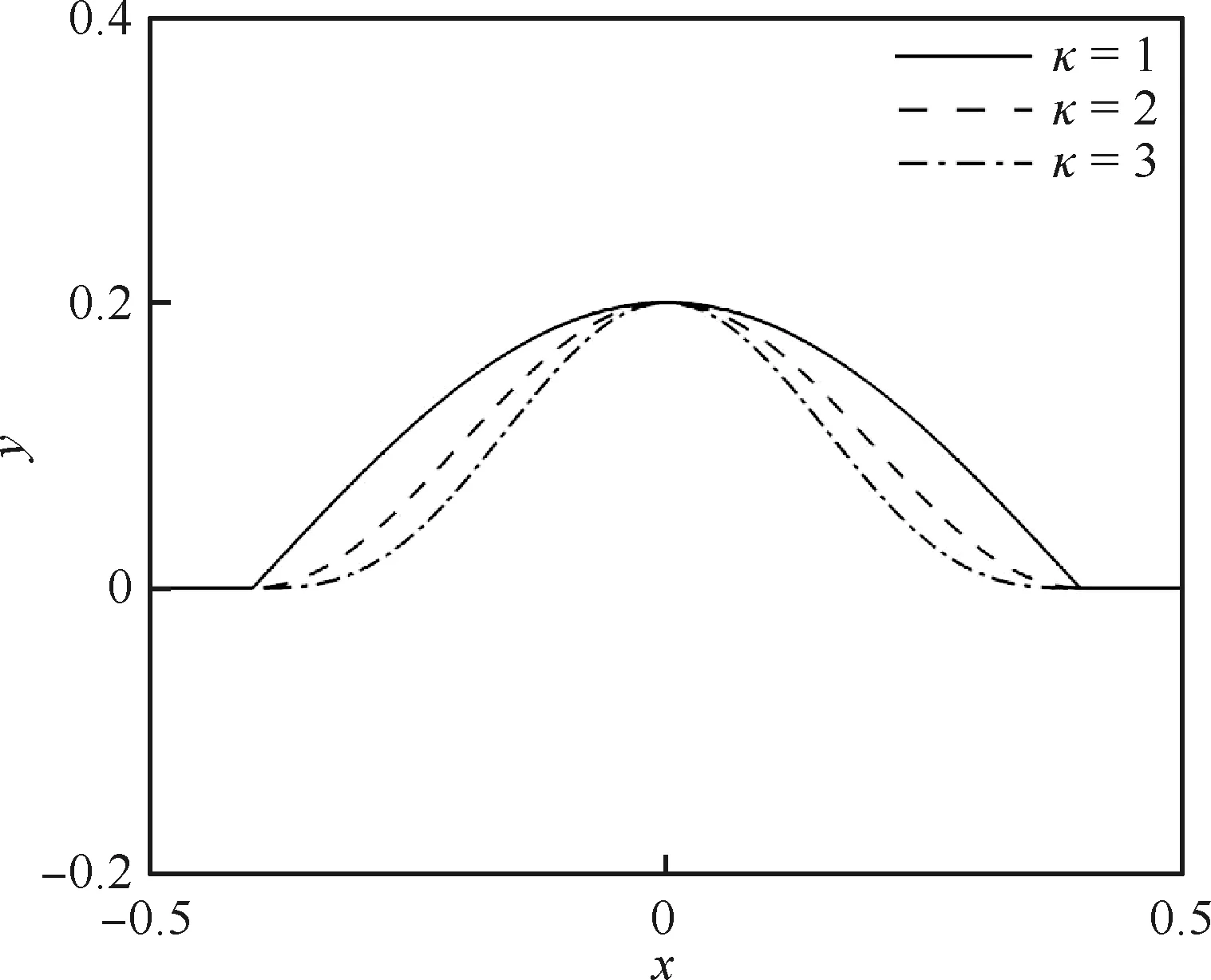
2.2 數值離散

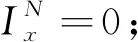
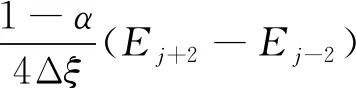

2.3 結果分析



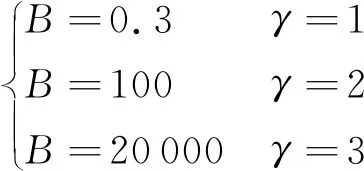


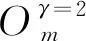
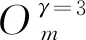
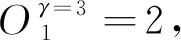
2.4 算例應用
3 結 論

