直升機后緣襟翼驅動器遲滯現象仿真與抑制

周金龍，董凌華，楊衛東

南京航空航天大學 航空學院，直升機旋翼動力學國家級重點實驗室，南京 210016

主動控制后緣襟翼(Actively Controlled Flap,ACF)是一種行之有效的直升機旋翼振動主動控制技術[1-3]。安裝在直升機槳葉后緣的襟翼在驅動器作用下動態偏轉，產生附加的氣動載荷，從而抵消部分旋翼振動載荷。整個后緣襟翼旋翼系統由基體槳葉、后緣襟翼以及附屬的驅動器組成，結構簡單緊湊，并且因為后緣襟翼的驅動機構位于旋翼上，與直升機操縱線系無直接聯系，后緣襟翼機構失效不會危及直升機飛行安全，相比其他形式的旋翼振動主動控制技術，如高階諧波控制[4](Higher Harmonic Control,HHC)和獨立槳葉控制[5-7](Individual Blade Control,IBC)，主動控制后緣襟翼可靠性更高，在當前技術條件下更具工程應用潛力。

由于后緣襟翼安裝在旋翼槳葉上并與之同步旋轉，同時承受氣動載荷和離心載荷的作用，并且需要在控制信號作用下作高頻偏轉，要求后緣襟翼驅動器在具有足夠的力和位移輸出性能的同時具有較寬的工作帶寬，給后緣襟翼驅動器的選擇和設計帶來挑戰。壓電材料具有輸出力大、工作頻率高的優點，因此現有的主動控制后緣襟翼旋翼方案多選擇帶有位移放大機構的壓電疊堆驅動器作為后緣襟翼的驅動元件[8-13]。但是壓電材料固有的遲滯特性使得期望襟翼偏角與實際襟翼偏角之間存在一定偏差，使襟翼偏轉運動與襟翼控制信號之間存在延遲。Viswamurthy等[14-16]使用經典的Preisach模型對壓電驅動器進行建模，并首先開展了驅動器遲滯對后緣襟翼振動控制性能影響分析，仿真結果顯示忽略驅動器遲滯效應將會對后緣襟翼最優控制率的預測帶來較大誤差，甚至可能會增大旋翼振動載荷。Mallick等[17]使用橢圓曲線對壓電驅動器進行建模，并研究了壓電驅動器非線性遲滯對振動控制效果的影響，研究結果顯示遲滯會在一定程度上降低后緣襟翼振動控制效果。Muir等[18-19]通過實驗研究了壓電驅動器動態遲滯特性，并采用經典Preisach模型研究了遲滯對大速度前飛狀態下后緣襟翼振動控制和噪聲抑制性能的影響，發現遲滯對開環狀態下噪聲控制性能影響明顯，但是對閉環狀態下振動和噪聲控制影響有限。

壓電驅動器的遲滯特性與壓電材料特性、驅動器結構等因素相關，不同壓電驅動器遲滯特性存在差異，對后緣襟翼旋翼振動控制性能的影響也不完全相同；并且壓電驅動器遲滯受驅動信號頻率的影響，經典的Preisach遲滯模型不具有率相關特性，難以模擬不同驅動頻率下后緣襟翼運動規律[20]；同時已開展的研究多集中在驅動器遲滯對振動噪聲抑制性能的影響方面，而較少有對后緣襟翼驅動器遲滯抑制的研究。Viswamurthy和Ganguli[16]采用經典Preisach模型的逆模型開展了驅動器遲滯補償仿真研究，經典Preisach模型計算量較大，并且由于經典Preisach模型的率不相關特性，難以精準模擬后緣襟翼多頻率控制輸入下襟翼偏轉運動遲滯現象。此外后緣襟翼偏角受襟翼離心載荷與驅動器遲滯影響，其中離心載荷對襟翼偏角影響是不可消除的，其影響大小取決于襟翼質量分布以及旋翼工作轉速，可以通過合理優化設計后緣襟翼結構、降低襟翼質量、減小襟翼鉸鏈摩擦等方式降低離心力對后緣襟翼偏轉角度的影響，而驅動器遲滯主要是由驅動器自身特性決定的，因此采用Bouc-Wen模型對應用于后緣襟翼旋翼的壓電驅動器進行了建模，并與帶后緣襟翼的旋翼動力學模型相結合，研究了壓電驅動器遲滯對主動控制后緣襟翼旋翼振動控制性能的影響；針對該驅動器的遲滯特性，建立了基于Bouc-Wen逆模型的前饋控制與PID反饋控制相結合的控制策略，顯著地抑制了該驅動器非線性遲滯，為后續的后緣襟翼旋翼設計與振動控制實驗奠定了基礎。

1 驅動器遲滯建模

由于壓電材料輸出位移較小，在實際應用時需要配合適當的位移放大機構，常見的位移放大機構如X型放大機構[8-9]、L型放大機構[11-12]以及菱形放大機構[10,13]等，由于菱形放大機構結構簡單，并且不存在機械間隙的影響，因此后緣襟翼多采用帶有菱形框或類似結構的放大機構的壓電疊堆驅動器。根據后緣襟翼旋翼需求研制的帶有菱形框放大機構的壓電疊堆驅動器如圖1所示。

該壓電驅動器安裝到后緣襟翼槳葉上，其固定端與旋翼槳葉固定安裝在一起，輸出端與后緣襟翼相連，并通過鉸鏈機構將驅動器輸出端的直線位移輸出轉換為后緣襟翼的偏轉運動。驅動器在一端固定一端自由的狀態下工作性能參數如表1 所示。

為研究該壓電驅動器遲滯現象，設置偏置電壓為40 V、幅值(零-峰值)為40 V的正弦驅動電壓，不同驅動頻率下該壓電驅動器遲滯如圖2所示。

圖1 壓電驅動器與后緣襟翼槳葉

表1 壓電驅動器參數

從圖2可以發現，該壓電驅動器驅動電壓與輸出位移之間存在明顯遲滯現象，并且隨著驅動頻率的提高，驅動器的遲滯逐漸增加，因此有必要對該驅動器遲滯特性進行建模分析，并研究其對后緣襟翼旋翼振動控制性能的影響。

常用的壓電材料遲滯模型有Preisach模型、KP(Krasnosel’skii-Pokrovskii)模型和PI(Prandtl-Ishlinskii)模型等，這些模型能夠較為準確地描述壓電材料的遲滯現象，但是由于其模型運算復雜，難以應用于實時控制系統。Bouc-Wen模型具有參數少、計算效率高的特點，因此本文采用Bouc-Wen模型[21-23]對應用于后緣襟翼的壓電驅動器進行遲滯建模。Bouc-Wen模型通過引入狀態變量h來描述系統的遲滯現象：

(1)

式中：遲滯曲線形狀受α、β和γ控制；u為施加到壓電堆上的電壓；d為驅動器有效逆壓電系數；n為模型的階數，為了降低模型的計算量，取n=1，式(1)簡化為

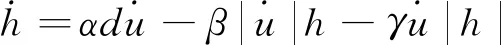
(2)

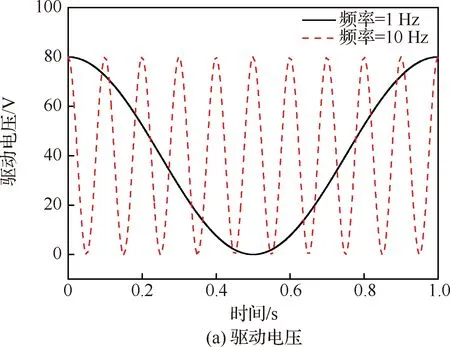
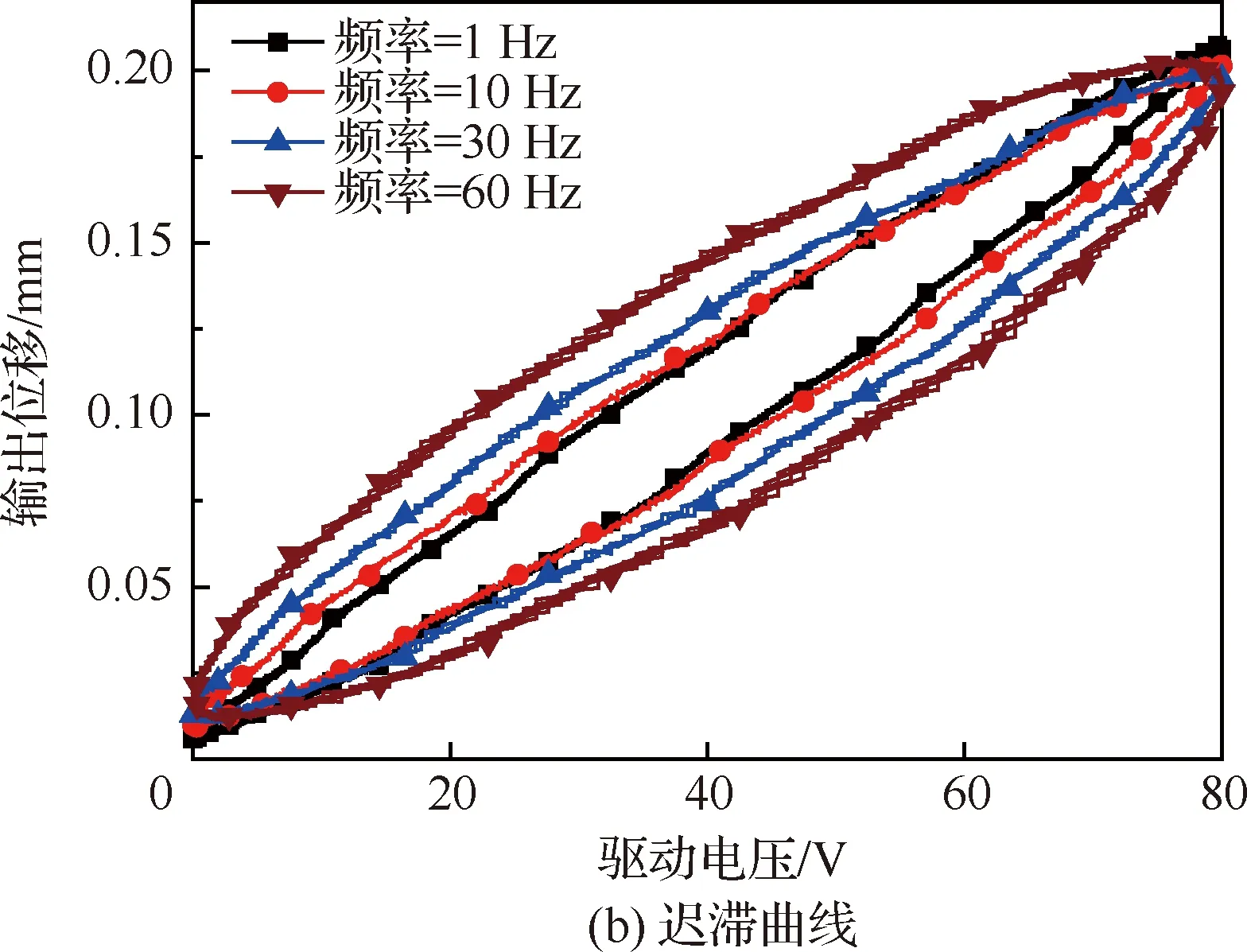
圖2 不同頻率下遲滯現象

在旋翼旋轉時，后緣襟翼會在氣動載荷作用下而發生被動偏轉，進而降低后緣襟翼的控制功效。為了減小后緣襟翼的被動偏轉幅度，需要驅動器具有較大的剛度特性。同時由于驅動器需要帶動后緣襟翼動態偏轉，其質量和阻尼特性也會影響其工作性能。考慮質量、阻尼和剛度特性的包括位移放大機構的壓電驅動器運動方程可表示為

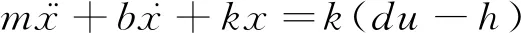
(3)

式中:m為壓電驅動器的有效質量;b為壓電驅動器阻尼;k為壓電驅動器剛度;x為驅動器輸出位移。包含位移放大機構的壓電驅動器Bouc-Wen模型如圖3所示。

在不考慮驅動器高階模態前提下，包含位移放大機構的整個驅動器動態特性可采用二階系統傳遞函數來描述。包含位移放大機構的壓電驅動器剛度k可以通過實驗測量的方式獲得。通過掃頻實驗獲得驅動器一階共振頻率fr后，根據系統固有頻率與質量、剛度之間的關系：

(4)

從而有：

(5)

包含位移放大機構的壓電驅動器輸入輸出特性主要由壓電疊堆的非線性遲滯和整個驅動器的動態特性決定，在低頻驅動電壓作用下，不同頻率下壓電驅動器遲滯曲線幾乎完全重合(圖4)，可以認為該驅動器在靜態或較低頻率下的遲滯現象主要由壓電材料自身遲滯特性決定，與整個驅動機構的動態特性無關，因此Bouc-Wen模型的辨識過程可以分為2步：①根據低頻驅動電壓下實驗測量遲滯數據辨識與壓電材料遲滯相關的模型參數；②在此基礎上根據較高頻率驅動電壓下實驗測量遲滯參數辨識與驅動機構動態特性相關參數。分步辨識減少了每次辨識過程中待辨識參數個數，提高了辨識精度和效率。

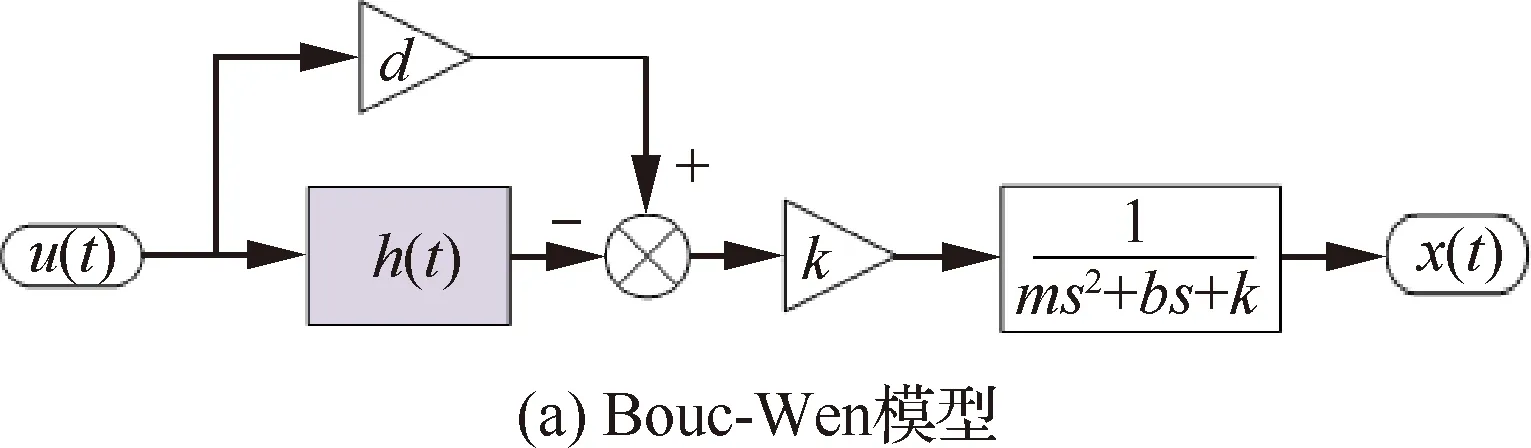
圖3 Bouc-Wen模型框圖

在低頻驅動電壓作用下，忽略整個驅動機構質量、阻尼和剛度對系統輸入輸出特性的影響，式(3)可以簡化為

x=du-h

(6)

此時Bouc-Wen遲滯模型有d、α、β和γ共4個未知參數。粒子群算法(Particle Swarm Optimization, PSO)具有搜索速度快、需調整參數少以及結構簡單的優點，因此本文采用粒子群算法辨識Bouc-Wen模型中的未知參數，建立適應度函數為

(7)

低頻下PSO辨識效果如圖6所示，結果顯示PSO辨識效果良好，建立的Bouc-Wen模型能夠較好地反映低頻下壓電驅動器遲滯現象。

以同樣的方式辨識高頻信號作用下驅動器遲滯參數，保持d、α、β和γ的值不變，此時式(3)表示的Bouc-Wen模型僅含有線性阻尼b一個未知參數。PSO辨識得到的Bouc-Wen模型參數如表2所示。10～60 Hz驅動電壓作用下Bouc-Wen模型輸出與實驗測量結果對比如圖7所示，從圖中可以看出，本文建立的Bouc-Wen模型能夠在較寬的頻率范圍內準確地描述帶有菱形放大機構的壓電驅動器遲滯現象。

圖4 低頻遲滯

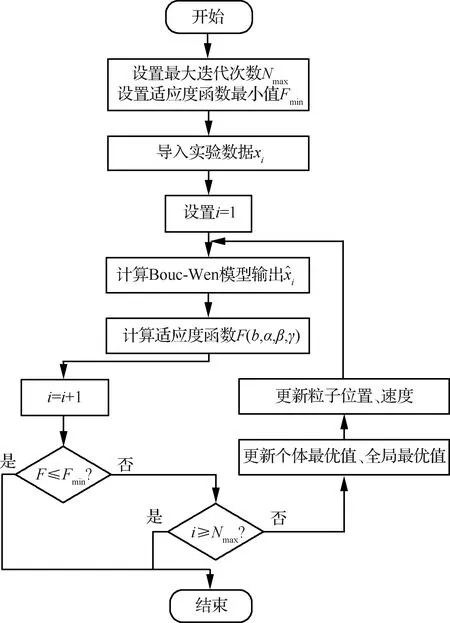
圖5 粒子群算法辨識流程

圖6 實驗結果與模型輸出比較(1 Hz)

表2 Bouc-Wen模型參數

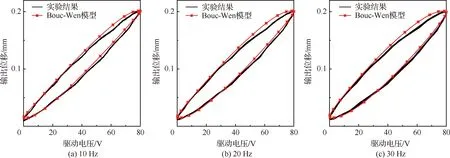
圖7 不同頻率下模型輸出與實驗結果比較

2 遲滯抑制

為了抑制壓電驅動器的遲滯現象，開展了基于Bouc-Wen逆模型的前饋控制研究。根據Bouc-Wen模型輸入電壓與輸出位移關系可得：

(8)

根據式(8)建立基于Bouc-Wen逆模型的前饋補償控制系統如圖8所示。以10 Hz前饋補償控制實驗效果為例(圖9)，從圖中可以看出，壓電驅動器遲滯現象都得到了顯著的抑制，但是遲滯現象并沒有被完全消除，驅動器位移輸出與期望位移之間存在一定偏差。

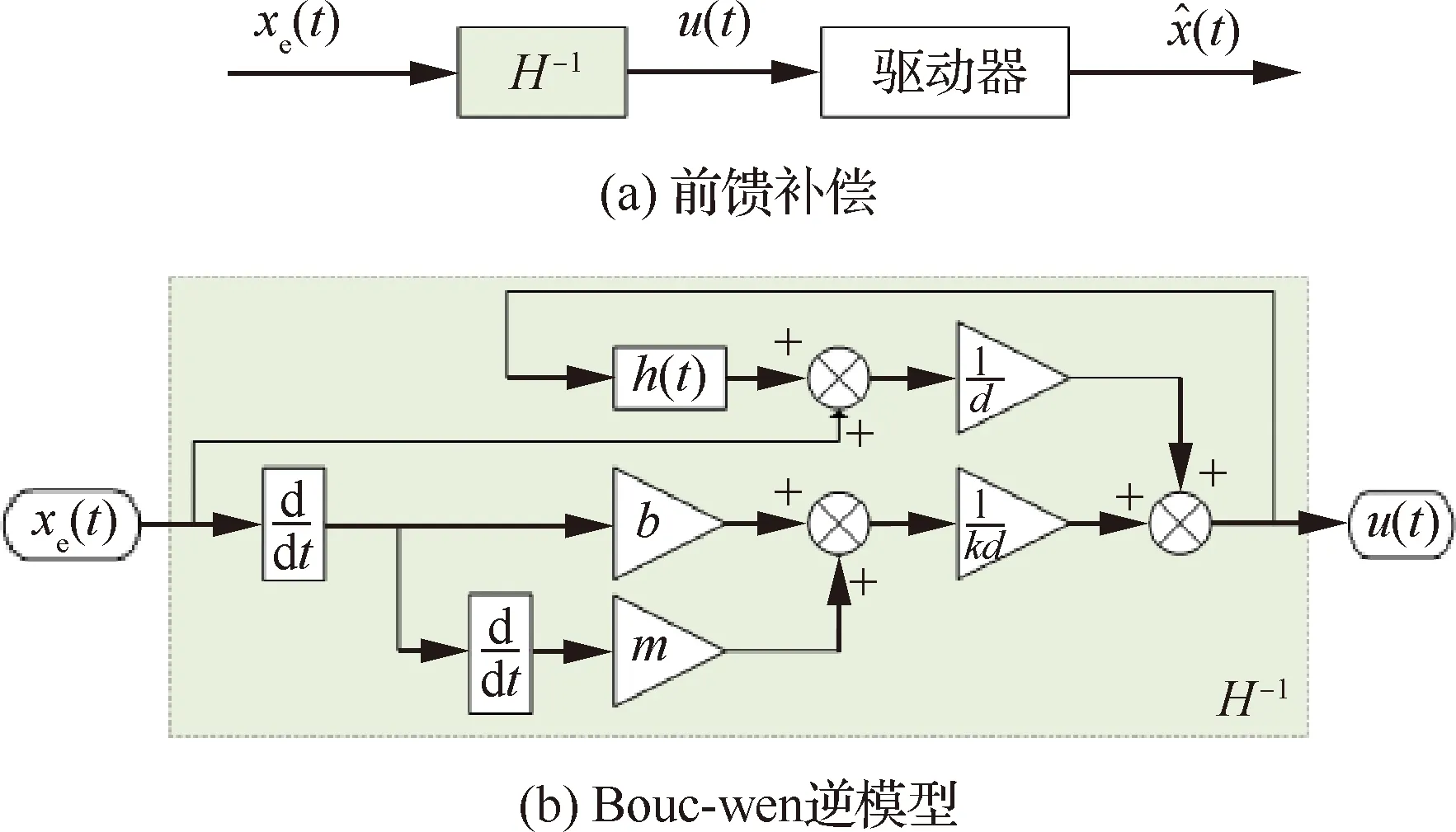
圖8 前饋補償

通過采用基于Bouc-Wen逆模型的前饋補償消除大部分的驅動器遲滯，然后使用PID控制來抑制由于建模誤差而殘余的遲滯，同時抑制由于外界擾動而引起的驅動器輸出位移與期望位移之間的誤差，從而提高驅動器輸出位移精度，采用復合控制后驅動器輸出位移與期望位移之間的偏差如圖12所示，從圖中可以看出，通過采用復合控制，驅動器位移輸出偏差進一步減小，整體誤差控制在5 μm以內。壓電驅動器復合控制效果如圖13所示，在10～60 Hz頻率范圍內，遲滯現象得到明顯抑制，實驗效果顯示所建立的復合控制策略具有良好的適應性，能夠應用于不同頻率工作的后緣襟翼旋翼。

圖9 前饋控制結果(10 Hz)

圖10 復合控制結構

圖11 實驗裝置

圖12 位移誤差

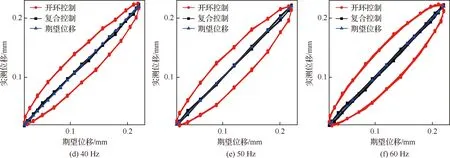
圖13 復合控制效果

3 驅動器遲滯對振動控制性能影響

為了研究驅動器遲滯現象對直升機后緣襟翼振動控制性能的影響，建立了考慮驅動器遲滯的直升機后緣襟翼氣彈耦合動力學模型，驅動器有/無遲滯狀態下的振動載荷計算如圖14所示。其中δf(t)為無遲滯的理想驅動器狀態下的后緣襟翼偏角；δ′f(t)為有遲滯驅動器狀態下的后緣襟翼偏角；z為旋翼槳轂振動載荷諧波系數向量。

圖14 驅動器有/無遲滯狀態下振動載荷計算

建模對象壓電驅動器滿足后緣襟翼旋翼驅動需求，并且在測試中表現出遲滯現象，因此以該驅動器遲滯特性為基礎建立考慮驅動器遲滯的旋翼動力學模型。在無遲滯理想驅動器情況下優化得到的后緣襟翼偏轉角度轉換成位移信號后激勵壓電驅動器，并采用復合控制抑制其遲滯現象，再將測量得到的驅動器位移輸出轉換為偏角后輸入到載荷計算模塊中，以半實物仿真的方式研究復合控制策略對后緣襟翼振動控制性能的影響。

考慮到后緣襟翼旋翼各個部件之間作用比較復雜，難以直接使用牛頓定律建立其運動方程，因此采用Hamilton原理建立包含后緣襟翼、旋翼在內的動力學方程：

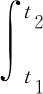
(9)

式中：δU為系統的虛位能；δT為系統的虛動能；δW為后緣襟翼旋翼在旋轉過程中受到的外載荷虛功。所建立的旋翼動力學模型主要包括基體槳葉和后緣襟翼2部分，因此式(7)中的虛位能、虛動能和外載荷做功為槳葉和后緣襟翼兩部分疊加而成：

(10)

(11)

(12)

式中：bi代表第i片槳葉；fi代表安裝在第i片槳葉上的后緣襟翼，整個旋翼系統共有Nb片槳葉。

基體槳葉氣動載荷采用查表法計算，根據所在翼型剖面處氣流速度與迎角，查詢對應翼型的氣動力系數表，通過插值的方式獲取相應的氣動載荷系數，而安裝有后緣襟翼的剖面處氣動載荷采用準定常Theodorsen帶襟翼翼型氣動模型計算。具體的旋翼動力學建模過程詳見文獻[24-25]，分別取前進比為μ=0.053和μ=0.140下旋翼動力學模型計算結果與SA-349直升機飛行實測結果對比[26](圖15)，結果顯示所采用的旋翼動力學模型具有較高的計算精度，適合開展帶后緣襟翼旋翼振動載荷計算。

本文采用離散時間高階諧波控制(Discrete-Time Higher Harmonic Control, DTHHC)算法開展后緣襟翼振動控制仿真，在穩態前飛條件下直升機后緣襟翼旋翼系統可視為周期時不變系統，后緣襟翼控制輸入與旋翼槳轂振動載荷響應滿足：

z=Tθ+z0

(13)

式中:θ為后緣襟翼控制輸入諧波(后緣襟翼偏角δf(t)或δ′f(t)經傅里葉級數展開后獲得);z0為后緣襟翼保持靜止時槳轂振動載荷諧波;T為系統傳遞矩陣，采用最小二乘法辨識T矩陣，辨識過程詳見文獻[25]。在考慮驅動器遲滯情況下辨識T矩陣時，后緣襟翼偏角信號在通過Bouc-Wen模型后再傳遞到載荷計算模塊，而在無遲滯理想驅動器情況下，后緣襟翼偏角信號直接傳遞到載荷計算模塊。由于驅動器遲滯的影響，在有/無驅動器遲滯情況下辨識得到的T矩陣發生了變化，相應的后緣襟翼最優控制率也將發生變化。

圖15 模型計算結果與飛行實測數據

建立振動控制目標函數：

J=zTQz+θTRθ

(14)

式中：Q和R分別為旋翼槳轂振動載荷輸出和后緣襟翼控制輸入權重矩陣。因為后緣襟翼偏轉角度受驅動器以及襟翼機構機械限制，并且襟翼的主動偏轉運動需要消耗能量，因此通過合理調整Q和R可以在振動控制效果和襟翼控制輸入間權衡取舍，以期達到綜合最優的控制效果。為了比較在驅動器有/無遲滯下后緣襟翼振動控制效果，在仿真過程中，矩陣Q和R均設置為單位矩陣。

當目標函數取極值時有

(15)

代入式(11)和式(12),整理得到后緣襟翼最優控制諧波：

θopt=(TTQT+R)-1TTQ(Tθ0-z0)

(16)

本文選取中等速度穩態前飛狀態開展仿真計算，旋翼槳葉和后緣襟翼參數如表3所示。考慮驅動器遲滯、不考慮驅動器遲滯以及采用復合控制的半實物仿真下后緣襟翼振動控制效果如圖16所示，Fx、Fy和Fz分別為x、y、z方向分力；Mx、My、Mz分別為x、y、z方向力矩。半實物仿真中期望襟翼偏角與復合控制開/關時襟翼偏角如圖17所示。

從圖16可以看出，在當前仿真計算飛行狀態下，驅動器遲滯會對后緣襟翼振動控制性能產生一定影響。雖然在驅動器無遲滯和有遲滯情況下后緣襟翼均具有良好的振動控制效果，但是相比于理想驅動器驅動下的旋翼振動載荷幅值，驅動器遲滯分別使Fx、Fy和Fz振動載荷幅值增大8.9%、7.9%和25.9%，Mx和My分別減小2.5%、3.7%，而Mz增大0.4%。雖然驅動器遲滯使Mx和My振動載荷幅值有所減小，卻使得其他振動載荷分量產生更大程度的增加，在一定程度上使得后緣襟翼的綜合減振性能有所降低。從圖16和圖17的半實物仿真結果可以看出，針對當前所采用的壓電驅動器，復合控制能夠有效地抑制驅動器遲滯對后緣襟翼偏角的影響，提高后緣襟翼振動控制性能。受槳葉內部的驅動器安裝尺寸限制，驅動器輸出功率有限，進而限制了后緣襟翼的偏角范圍，在不改變已有的后緣襟翼驅動器的基礎上能夠盡可能充分利用驅動器有限的輸出功率，提高振動控制效果，對于后緣襟翼研究是有意義的。

表3 旋翼與后緣襟翼參數

圖16 考慮與不考慮遲滯情況下的振動控制效果

圖17 襟翼偏角

4 結 論

針對帶菱形位移放大機構的壓電驅動器，通過實驗研究了其在動態驅動電壓下的遲滯現象；采用Bouc-Wen模型對該壓電驅動器遲滯進行了建模，并將遲滯模型與旋翼動力學模型相結合，研究了遲滯對后緣襟翼振動控制性能的影響；為提高后緣襟翼振動控制性能，開展了驅動器遲滯抑制研究，建立了基于Bouc-Wen逆模型的前饋控制與PID反饋控制的復合控制策略，得到如下結論：

1) 壓電驅動器在動態驅動電壓作用下表現出的遲滯現象具有明顯的率相關特性，隨著驅動信號頻率的升高，遲滯現象更加顯著，仿真研究表明在中等速度穩態前飛狀態下，驅動器遲滯會影響后緣襟翼振動控制效果。

2) 粒子群算法能夠有效辨識Bouc-Wen模型參數，建立的Bouc-Wen模型能夠在較寬的頻率范圍內較為精確地描述該壓電驅動器的遲滯現象。

3) 采用基于Bouc-Wen逆模型的前饋控制與PID反饋控制的復合控制策略能夠顯著地抑制該壓電驅動器的遲滯現象，驅動器位移輸出誤差控制在5 μm內，并且該控制策略在10～60 Hz頻率范圍內具有良好的適應性。