關于受到隨機擾動影響的帶有時滯的捕食模型的穩定性分析


摘 要:本文的主要目的是研究捕食者-食餌系統Lotka-Volterra模型解的穩定性。通過構造適當的李雅普諾夫泛函,利用積分公式,得到了平衡點的許多穩定性條件。本文所提到的這種方法已經用來研究SIR流行病模型的穩定性,其實將這種方法應用于一個新的模型也是我們本篇文章的一個特點及難點所在。因此,我們利用該方法在研究Lotka- Volterra模型的漸近均方穩定性上得到一個新的條件。最后,我們舉了兩個例子來驗證我們的理論性成果。
關鍵詞:捕食者-獵物模型;李雅普諾夫泛函;積分公式;時滯;隨機擾動
1.引言
?捕食者-捕食模型,這是最著名的生物數學模型之一。特別是近年來,它得到了廣泛的研究和應用。通過對模型的研究,我們可以充分了解生態系統的穩態問題。因此,我們研究了該模型在白噪聲類型隨機擾動下與帶有時滯的平衡點的穩定性問題。事實上,捕食者-食餌模型近年來得到了廣泛的研究,為了更好地理解,我們找到許多關于這一主題的文章,比如[1]主要研究了白噪聲下某些捕食模型的振蕩現象,[2]研究了帶有接種疫苗的確定性SIS流行病模型的穩定性,文獻[3]深究接種疫苗型隨機SIS流行病模型。[4]和[5]得出了擴散捕食者-食餌模型具有延遲的穩定性,研究了Lotka-Volterra模型的穩定性,并在[6,7]中證明了Hopf分岔的存在條件。事實上,Shaikhet已經在[8]中研究了捕食者-食餌系統的Lotka-Volterra模型的穩定性,但我們通過構造Lyapunov函數來發現與其條件不同的穩定性參數條件,該方法的特點是尋找合適的Lyapunov函數來處理時滯對系統的影響。
4.實例
?為了驗證我們的理論結果,即系統(1.6)的漸近穩定性和系統(1.5)的依概率穩定性,我們將使用數值模擬法來驗證穩定,我們主要用歐拉法對方程進行離散,然后用MATLAB進行繪圖。下面有兩個例子來說明我們的觀點。
例1.為了證明線性系統(1.6)的零解是漸近穩定的,我們取參數值,接下來,我們用數值模擬說明穩定性。在此參數條件下
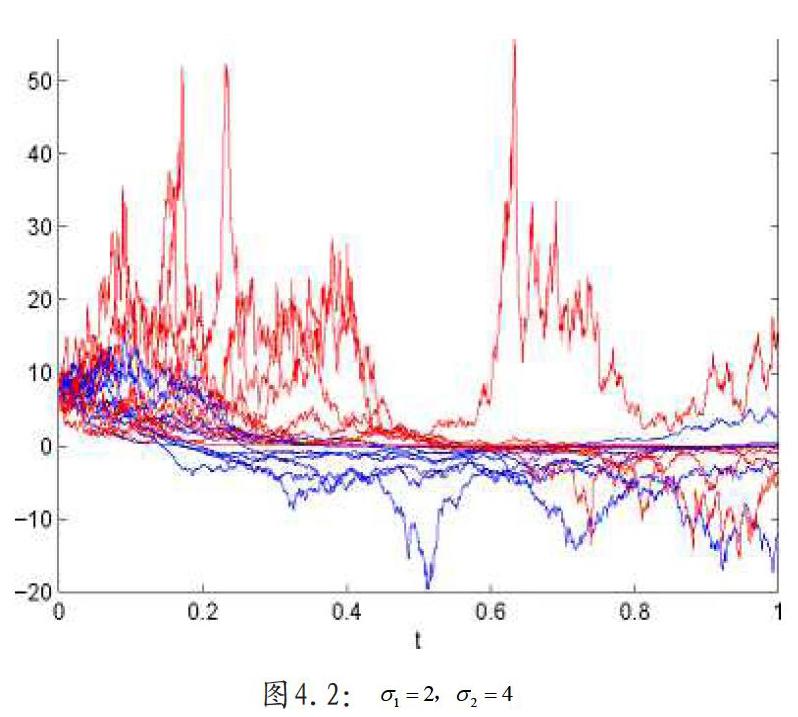
如果我們取通過計算得到0.36 < 2.8,0.64 < 10.5,滿足定理3.1.也就是說此參數條件下系統(1.6)是漸近均方穩定的.但是,如果選擇參數值,我們卻得到4 >2.8,16>10.5,不滿足定理3.1,換句話說,系統(1.6)不穩定.然后我們分別畫出不同參數值下的圖像,圖4.1和圖4.2.
從這個例子中,我們可以得出結論,當滿足定理3.1的條件時,給定初始值的系統(1.6)的零解最終是漸近穩定的,如圖4.1所示,不滿足定理3.1的條件,系統(1.6)的零解是不穩定的,如圖4.2所示。
參考文獻
[1]Raj M,Selvam A,Janagaraj R,Stability in a Discrete Prey-Predator Model,IJLERA 2,2013,Issue 1:482-485.
[2]Zhao Y,Jiang D Q,Regan O,The Extinction and Persistence of the Stochastic SIS Epidemic Model with Vaccination,Phys.,2013,392:4916?4927.
[3]Lin Y G,Jiang D Q,Wang S,Stationary Distribution of a Stochastic SIS Epidemmic Model with Vaccination,Phys.A,2014,394:187-197.
[4]Wu D Y,Zhao H Y,Yuan Y,Complex Dynamics of a Diffusive Predator-Prey Model with Strong Allee Effect and Threshold Harvest?ing,J.Math.Anal.Appl.,2019,469:982-1014.
[5]Zhang X B,Zhao H Y,Dynamics Analysis of a Delayed Reaction?Diffusion Predator-Prey System with Non-Continuous Threshold Har?vesting,Mathe.Biosci.,2017,289:130-141.
[6]Yan X P,Zhang C H,Hopf Bifurcation in a Delayed Lokta-Volterra Predator-Prey System,Nonlinear Anal.:Real World Appl,2008,9:114?127.
[7]Xu C J,Bifurcation Analysis in a Lotka-Volterra Model with Delay,Elixir Appl.Math.,2011,38:4312-4314.
[8]Shaikhet L,Lyapunov Functionals and Stability of Stochastic Function?al Differential Equations.Springer,Dordrecht,Heidelberg,New York,London,2013.
[9]Shaikhet L,Stability of the Neoclassical Growth Model under Perturba?tions of the Type of Poisson's Jumps:Analytical and Numerical Anal?ysis,Commun.Nonlinear SCI.Numer.Simulat,2019,72:78-87.
[10]Beretta E,Kolmanovskii V,Shaikhet L,Stability of Epidemic Model with Time Delays Influenced by Stochastic Perturbation,Math.Comput.,1998,45:269-277.
[11]Kolmanovskii V B,Nosov V R,Stability of Function Differential Equa?tions,Academic Press:New York,1986.
[12]Kolmanovskii V B,Myshkis A D,Applied Theory of Functional Differ?ential Equations,Kluwer Academic Publishers:Boston,1992.
[13]Shaikhet L,Stability in Probability of Nonlinear Stochastic Hereditary Systems,Dyn.Syst.Appl.,1995,4(2):199-204.
作者簡介:
陳楊,女,(1995-),漢,山東省濟南市,碩士研究生,研究方向:生物數學,動力系統

