漂浮式光伏電站漂浮方陣多點系泊特性研究
肖 福 勤,孔 耀 華,余 德 海,吳 昊,陳 作 鋼,4
(1.淮南陽光浮體科技有限公司,安徽 淮南 232000; 2.陽光電源股份有限公司,安徽 合肥 230088; 3.上海交通大學 海洋工程國家重點實驗室,上海 200240; 4.高新船舶與深海開發裝備協同創新中心(船海協創中心),上海 200240)
1 研究背景
《國家能源發展“十三五”規劃》[1]將光伏發電列為重點發展領域之一,制定了2020 年太陽能發電規模達到1.1億千瓦以上規模的目標,并鼓勵利用采煤沉陷區廢棄土地建設光伏發電項目, 截止目前實際已超額完成任務。2016年Sahu A等[2]根據安裝環境對了光伏發電系統進行了分類,介紹了漂浮式光伏電站的組成和設計關鍵。2017年王方毓[3]對水上光伏電站的現狀以及特點進行了介紹,將水上光伏電站按工作水深分為打樁架高式光伏電站和漂浮式光伏電站,介紹了漂浮式光伏電站的結構形式及錨固方式。固定式光伏電站采用樁基固定,出于成本考慮只適用于淺水水域。相對而言,漂浮式光伏電站具有更加廣闊的發展空間,漂浮式光伏電站為新興應用,國內外對其各方面的研究仍處于起始階段,漂浮式光伏電站的全球安裝量在2016年后才進入快速增長期[4]。由于其自身漂浮的特點,漂浮式光伏電站在自然環境中容易受到大風、水流以及波浪等影響,使得其發生平移或旋轉,對光伏電站的經濟性和安全性造成危害。
由于漂浮式光伏電站剛剛興起,國內外仍未見關于其系泊問題的系統性研究內容發表。以色列Solaris Synergy公司對于飄浮式光伏電站的姿態以及定位是通過一種名為Grid-Based Solaris Synergy system的布線控制系統來實現[5],該系統通過方陣四周網狀的線纜獨立控制漂浮方陣的各個部分,達到控制漂浮方陣的目的(見圖1)。但他們未給出系泊強度計算的相關研究,同時該解決方案僅適用于中小型的漂浮式光伏電站。國內陽光電源(SUNGROW)則直接在漂浮方陣四周布置錨固點,通過鋼絲繩系泊纜與水底的錨點連接[6],如圖2所示。本文基于該類系泊系統對漂浮式光伏電站的多點系泊系統進行系列研究。
對于系泊線的受力分析方法,1960年Walton[7]提出的集中質量法是應用較廣的方法之一,在數值方法上屬于有限差分法。集中質量法中將錨泊線看作由無質量彈簧連接的離散集中質量組成,集中質量的節點承受錨泊線的外力。1968年Coliipp[8]采用該法對系泊纜繩的靜力平衡狀態進行了計算。Nakajima[9]對多成分錨泊線集中質量法進行了詳細介紹。Boom[10]對錨鏈動力問題采用集中質量法進行了研究。Orgil[11]在集中質量法的有限差分基礎上,對水平張力進行迭代求得系泊線的靜力特征參數。YING等[12]將集中質量法用于海洋工程柔性立管的靜力分析。此外,通過基于有限元法的靜力分析,Charles[13]計算了纜索的非線性靜力方程,楊敏東[14]對海洋系泊纜的靜平衡特性及張力分布進行了分析。
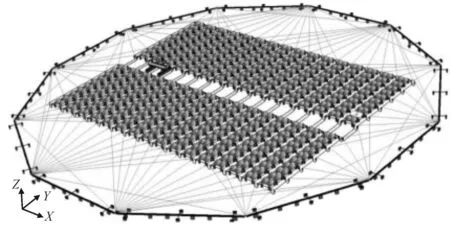
圖1 布線控制系統[5]

圖2 SUNGROW錨固系統[6]
2 理論介紹及坐標系
2.1 流載荷及風載荷
基于計算流體力學(CFD)方法,分別建立漂浮方陣的水下及水上部分的疊模計算模型,計算漂浮方陣的定常流載荷及風載荷。建立不可壓縮牛頓流體的連續方程和運動方程即Navier-Stokes方程,并對變量分解成脈動量及時均量兩個部分,對方程兩邊同時取系綜平均,得到平均后的連續方程及顯性表示的附加脈動應力的Navier-Stokes方程:
(1)
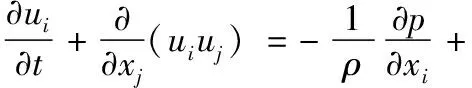
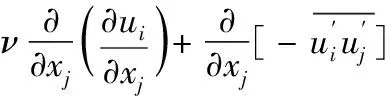
(2)
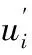
(3)
式中各量均采用國際單位制,其中,A為特征面積,m2,取單位面積1;v為風速或流速,m/s。
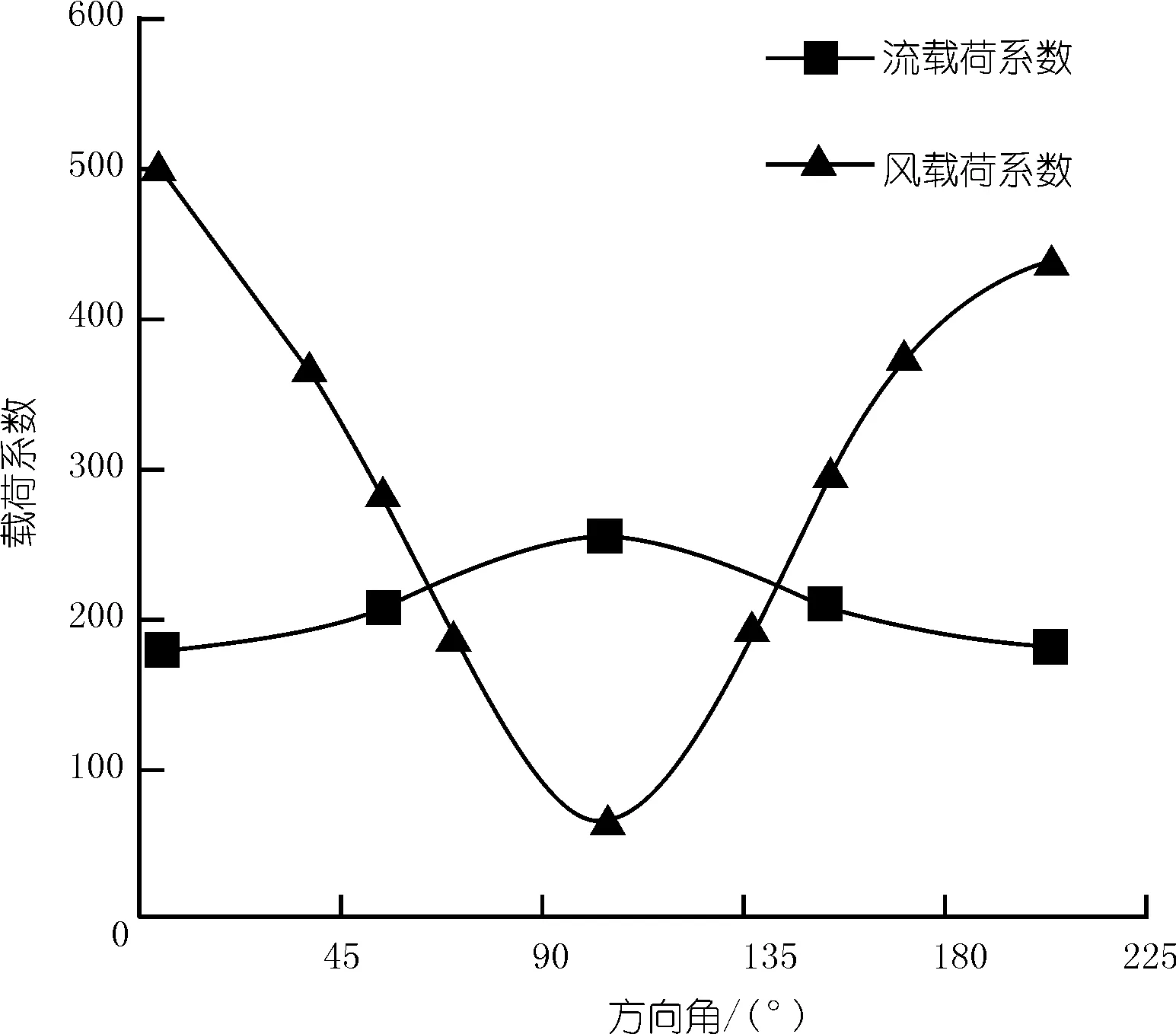
圖3 載荷系數曲線
2.2 波浪載荷
漂浮方陣可看作具有大量浮體的多浮體問題,每個浮體間的連接可看作有一定柔性,整體上對載荷具有緩沖吸收作用,但在計算上若考慮這種作用則將難以求解。本研究通過固化方陣,采用勢流理論對漂浮方陣波浪載荷進行計算,這種方法求解簡便,同時結果偏保守。
根據勢流理論,波浪作用在物體上的流體壓力分為兩部分:一部分是傅汝德-克雷洛夫力(F-K力),即由未受擾動的壓力場引起的壓力;另一部分是繞射力,即因為物體改變了此壓力場而產生的力。相應的總速度勢φ分解為入射勢φI和繞射勢φD:
φ=φI+φD
(4)
把繞射勢φD的時間部分和空間部分分離,再對物面進行數值離散,用離散量代替連續變量進行數值求解。
物體表面上的壓力分布為
(5)
作用在方陣物面上的波浪力可通過壓力分布沿濕表面SH的積分得到:
(6)
式中,nk為離散后每個物面的單位法線向量。
2.3 系泊纜靜力學方程
取某根錨泊線上微元如圖4所示,假設其在以錨泊點為原點的直角坐標系xoz下,且該微段中線距原點長度為s,微段長度為ds,一端切線與水平面夾角為φ。該微段上作用有重力、浮力、流體力以及自身張力。圖4中E為材料彈性模量,A為系泊纜截面積,ρ為流體密度,T為張力,W為系泊纜單位長度重量。
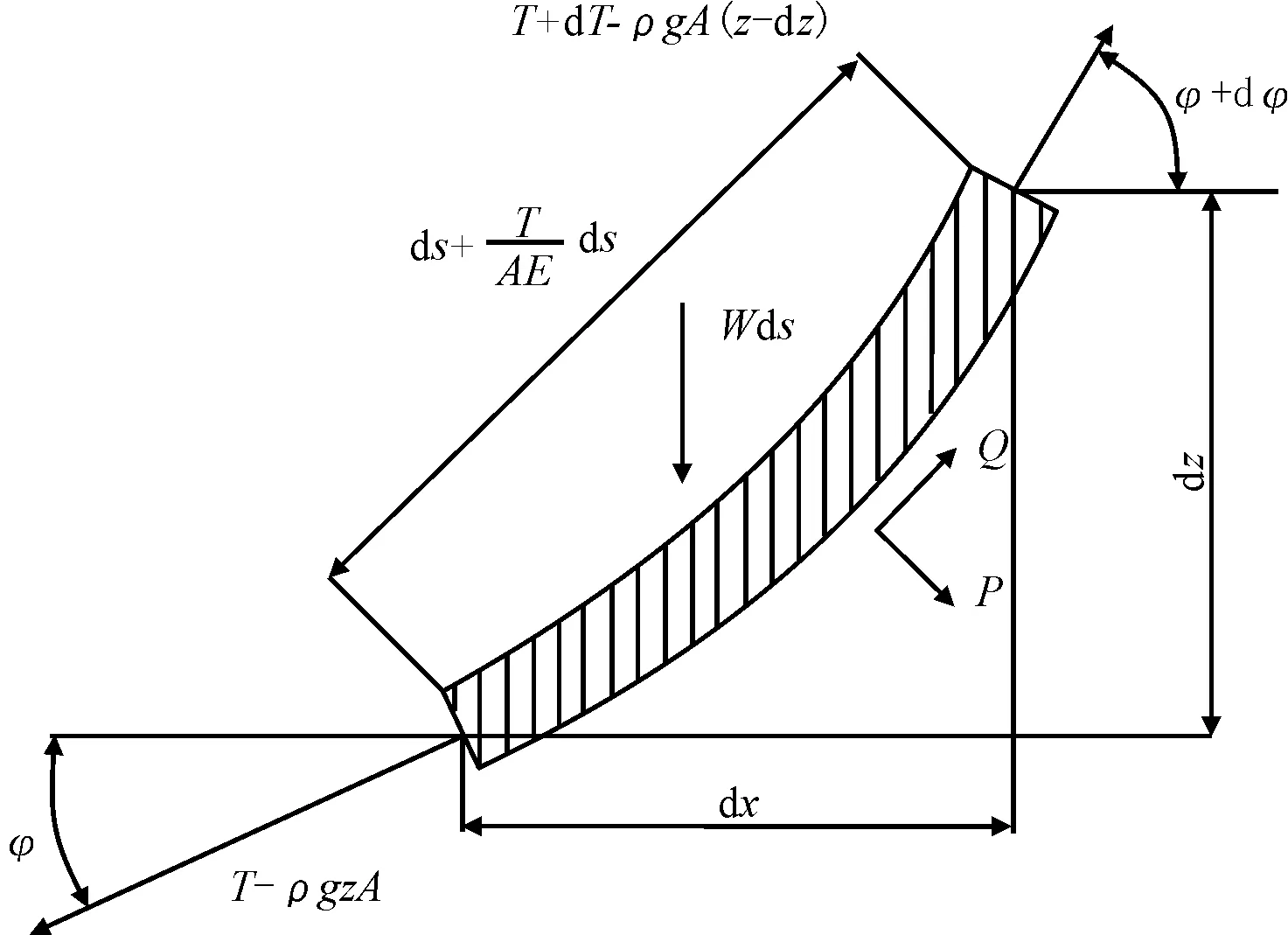
圖4 錨泊線微元受力
環境載荷下的漂浮方陣處于平衡狀態時,系泊纜處于靜止狀態,湖泊水下流動較弱,錨泊線遭受的流體作用相比于所受張力可忽略,若不考慮流體對錨泊線的作用,則滿足如下靜力學方程:
(7)
可進一步得到漂浮方陣整體載荷與方陣邊緣系泊點最終位置的關系。式(8)為系泊纜張力T與水平載荷TH之間的關系,式(9)為方陣系泊水平跨距X與水平載荷TH之間的關系。
T=TH+Wh+(W+ρgA)z
(8)
(9)
式中,h為水深,l為錨泊線總長。已知方陣所受水平載荷后,根據以上兩式可得漂浮方陣在極端條件下處于平衡狀態時系泊纜所受張力及方陣偏移。
2.4 方陣及坐標系
光伏電站位于煤礦塌陷區形成的湖泊,其水深變化為2.5~11.0 m。漂浮方陣簡化為尺寸為170 m×170 m的剛性方陣,電站的逆變升壓浮臺位于漂浮方陣的北側。如圖5所示,載荷方向規定如下:0°指載荷從北側指向南側,方向度數隨逆時針增加,從南側指向北側為180°,載荷力的方向參照xoy坐標系。多點系泊系統的布置圖如圖6所示,在方陣邊緣等間距布置系泊點,在一定水平跨距外的水底布置有錨點。系泊纜為公稱直徑20 mm的鋼芯鋼絲繩6X19S+1WR,質量為1.55 kg/m,軸向剛度2.2×104kN。
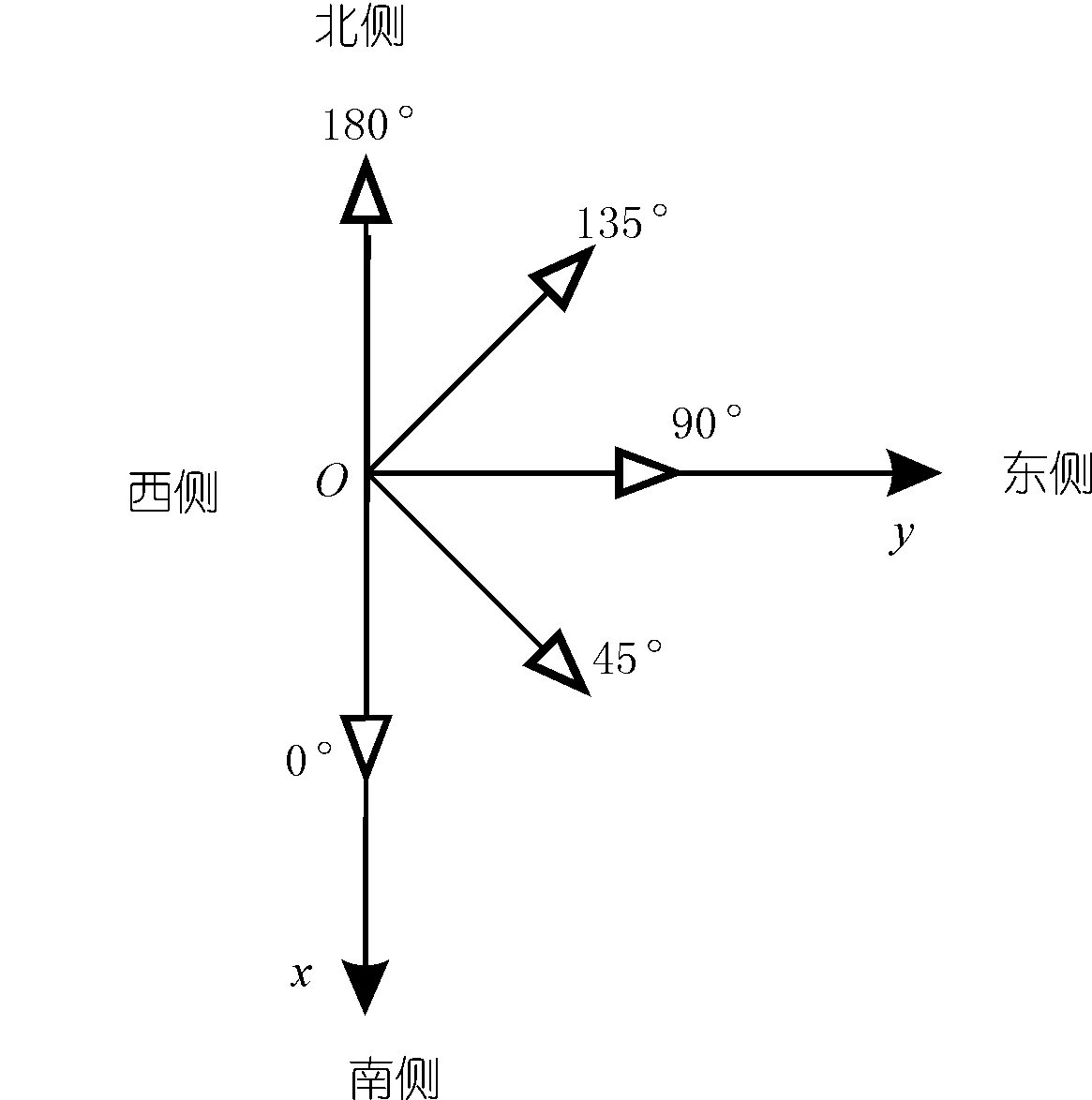
圖5 方陣坐標及載荷方向

圖6 多點系泊布置
3 水平跨距的影響
3.1 布置方案及環境
為研究水平跨距對方陣在極端環境下的錨泊線張力及偏移情況的影響,給出兩種水平跨距的多點系泊布置方案如表1所示。極端環境設置為風速30 m/s,流速0.18 m/s,浪高1.3 m。

表1 不同水平跨距布置方案
3.2 張力與偏移計算結果
假設風浪流同向,對0°,45°,90°,135°,180°五個載荷方向角,采用CFD方法進行流載荷與風載荷的數值模擬,采用勢流理論求得波浪載荷,對錨泊狀態下漂浮方陣進行錨泊靜力計算,且僅考慮水平面3個自由度。
為考察各載荷方向下方陣主要受力側(0°時為北側,45°時為北側與西側)系泊纜張力隨水深和水平跨距變化情況,繪出系泊纜張力分布如圖7所示,圖中系泊纜編號規則為:最東端及最南端為編號1,東至西、南至北依次增加。
系泊纜布置方式為每兩根纜繩對應一錨固點,每對纜繩中的兩根纜繩朝向不一致,45°方向角下,主受力的北側與西側的系泊纜各有一半先達到緊繃狀態,主要受力側的系泊纜張力分布呈鋸齒形如圖7(b)所示,故在其余系泊纜張力分布中,每一錨固點對應兩根纜繩中僅取張力較大的一根繪出。
0°載荷下北側各系泊纜張力分布較為均勻,其中跨距18.8 m的情況,高水位(11.0 m水深)時系泊纜張力較最低水位(2.5 m水深)時高約20%。對于同等水平載荷,在平衡狀態下系泊纜張力的水平分量不變,但由于水位越高,系泊纜俯角越大,導致總張力越大。故對于相同的布置方案,水深不同時出現的張力差異來源于系泊纜的俯角變化。由于方陣載荷沿各方向具有差異,45°載荷北側和西側系泊纜張力大小亦出現差異,但分布規律相同,即西北角的系泊纜張力最大,遠離載荷方向的系泊纜張力逐漸減小。
對于同是高水位11.0 m時兩種不同跨距布置,跨距14.79 m時的張力普遍高于跨距18.8 m的張力,該情況的出現亦是由于跨距較小的布置方式在相同水位情況下系泊纜俯角更大,導致張力合力更大。
在湖面上布置漂浮式光伏電站時需考慮電站方陣的位移范圍,以便規劃電站與電站或與其它結構物間的距離,因此計算方陣在極端載荷下的最大偏移具有重要意義。增大方陣的水平跨距除了有利于減小系泊纜張力,也有助于減小最大方陣偏移量,示意見圖8。繪出兩種方案中最低水深時方陣在各載荷方向下的最大偏移雷達圖如圖9所示。最低水位的45°載荷方向下方陣偏移最大,該現象是由最低水位系泊纜的較大余量以及45°載荷時系泊纜受力特點共同決定的。
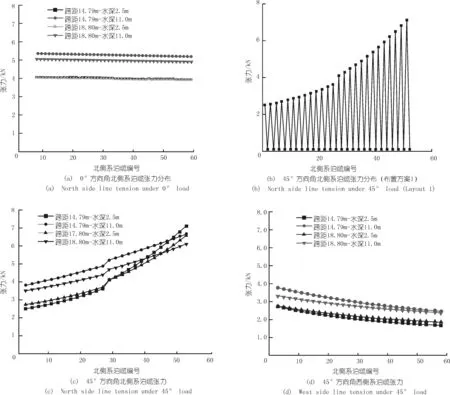
圖7 系泊纜張力分布
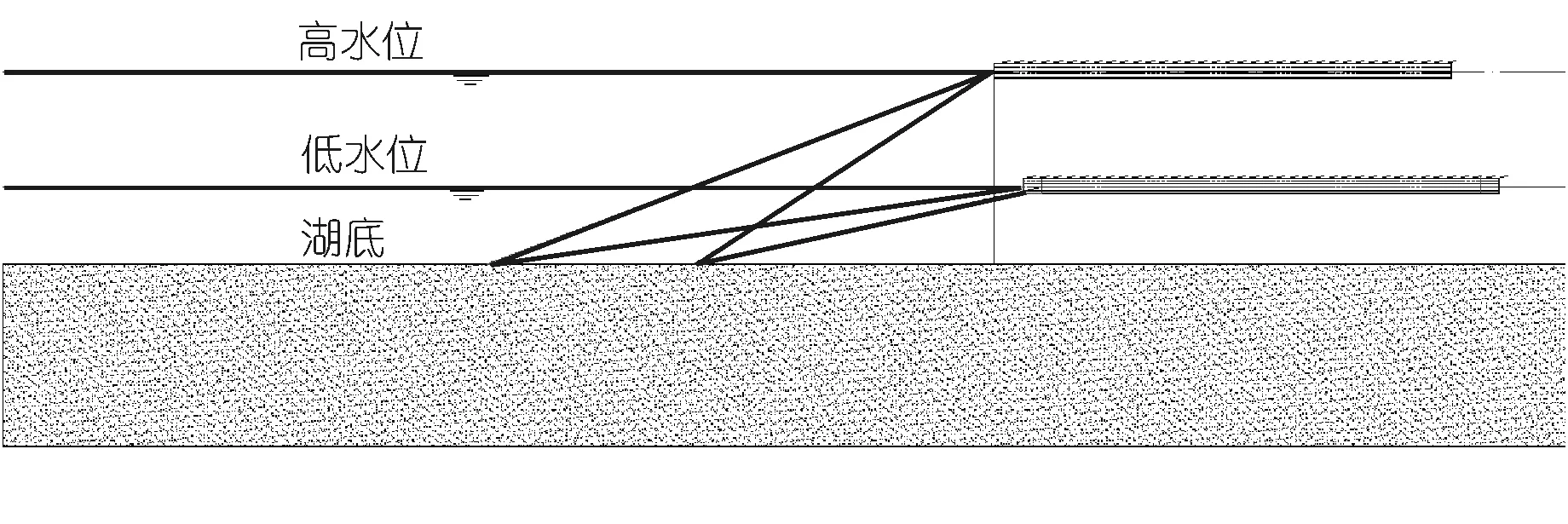
圖8 水平跨距對最大偏移的影響
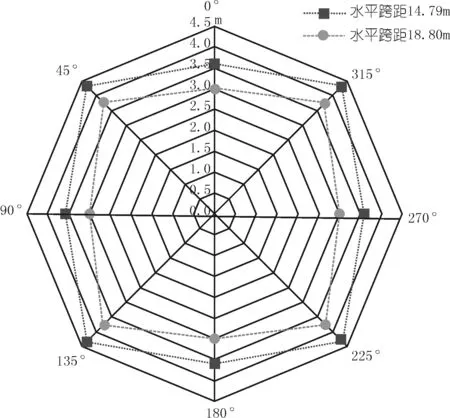
圖9 方陣各方向最大偏移量
4 布置間隔的影響
4.1 布置方案及環境
系泊布置間隔決定了方陣多點系泊中系泊纜的數量,為探究系泊間隔對系泊系統的影響,設定了兩種方案如表2所示,其中方案b系泊間隔為方案a的兩倍。環境設置為風速30 m/s,流速1 m/s,浪高1.3 m。

表2 不同系泊密度布置方案
4.2 張力特性
該系泊系統的方陣偏移規律在上節已進行探究,系泊布置間隔的影響主要體現在系泊纜張力上的影響上。計算得到兩種系泊間隔方案在極端環境下各系泊纜的張力分布,繪于圖10。由于方案b系泊間隔較大,故系泊纜數量減少約50%。為便于比較兩方案中相近位置的系泊纜張力,在繪制時方案b的張力曲線橫坐標軸采用圖上方的編號坐標軸,而方案a采用圖下方的編號坐標軸。
相對于方案a,方案b由于系泊纜數量的減少,每根系泊纜張力均有所增大。系泊纜數量減少約50%的方案b在0°方向角下張力增大約一倍。而在45°方向角下,由于系泊纜密度的減少,方案b的漂浮方陣偏移達到靜平衡后,接近西北角的系泊纜張力增加幅度大于位于載荷方向遠端的系泊纜。總體上看,系泊纜數量減少將使得極端環境下的系泊纜張力增大,且由于斜向載荷方向時載荷方向近端的系泊纜張力增幅更大,若要校核系泊纜與連接處的強度,應以載荷方向近端的系泊纜張力為準。
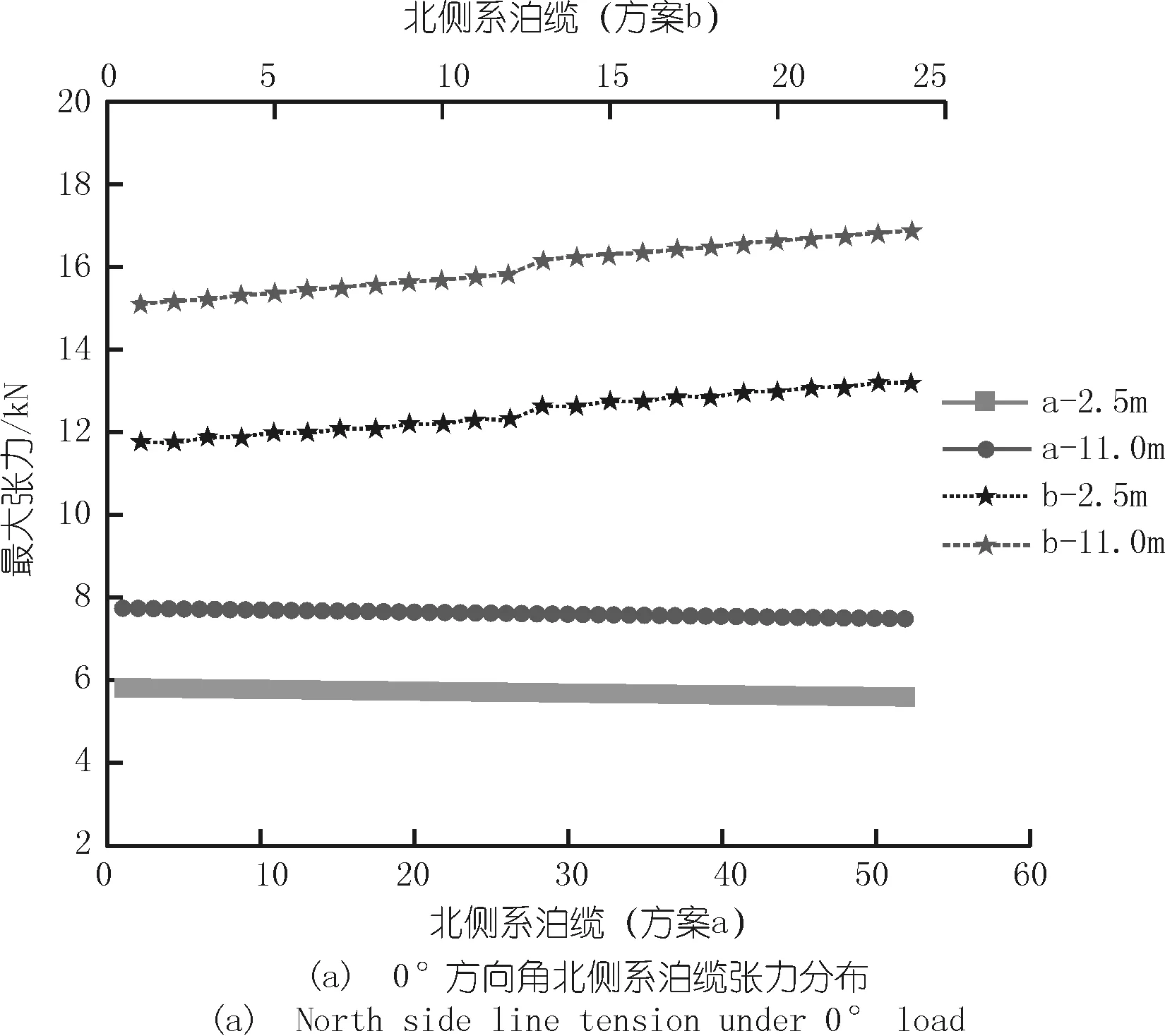

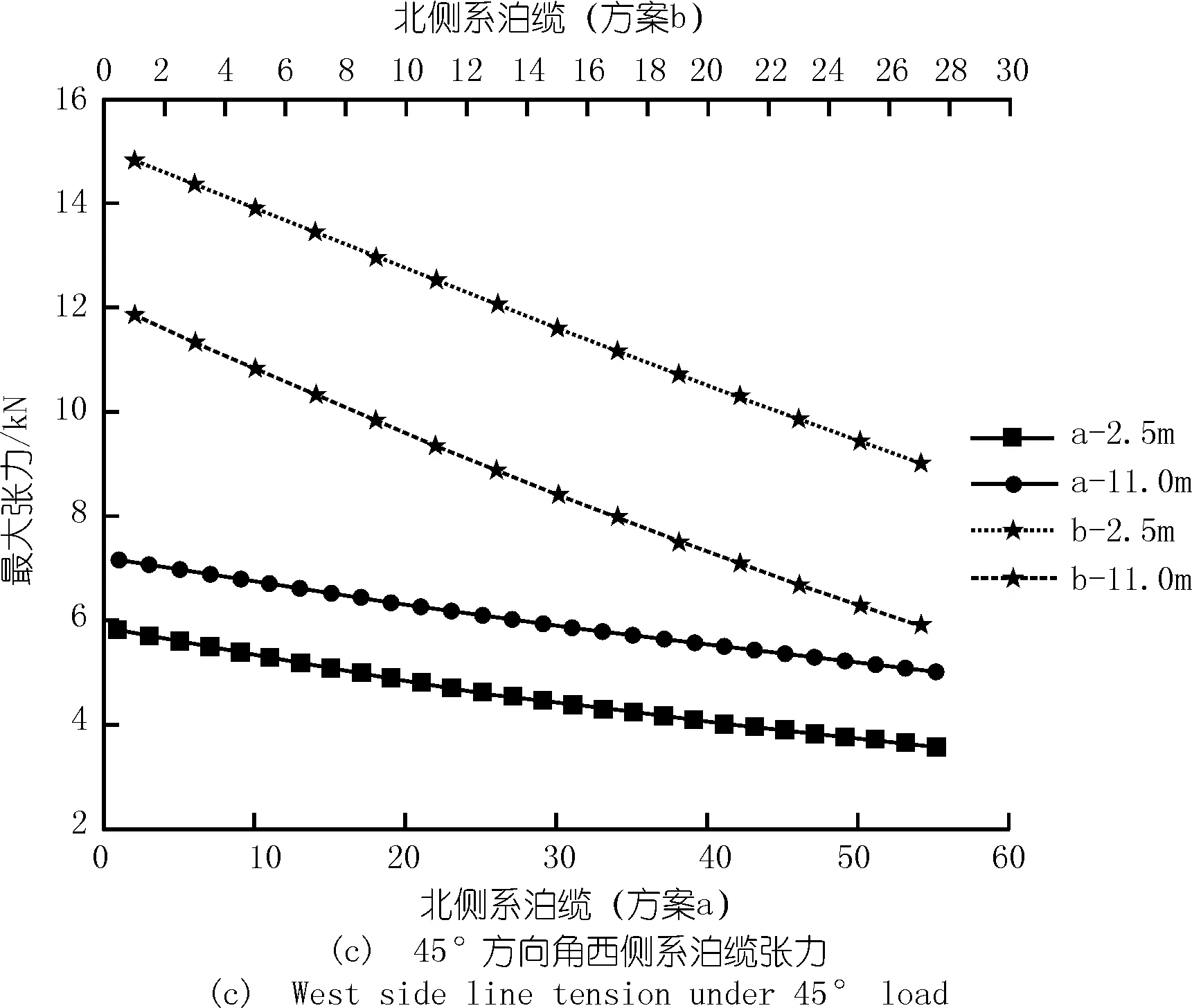
圖10 系泊纜張力分布
5 結 論
(1)浮式光伏電站在水位變化較大的水域進行工作時,對于相同的環境載荷,高水位時系泊纜張力大于低水位時系泊纜張力,校核安全性時應以最高水位狀況進行。在滿足系泊安全的前提下,由于高水位下系泊纜張緊程度高,漂浮方陣的偏移量較小;低水位下系泊纜松弛余量提供了較多的偏移空間,故對于方陣偏移帶來的問題考察時應以低水位情況進行。
(2)系泊水平跨距越大,系泊纜俯角越小,在靜力平衡時系泊纜總張力越小。對于相同的低水位情況,水平跨距大的系泊系統漂移方陣偏移越小。系泊系統在水平跨距的選擇上,應全面考慮對張力和偏移的需求。增大水平跨距一方面可減少極端環境時的系泊纜張力;另一方面可減少低水位時漂移方陣的最大偏移。但水平跨距的增加直接導致單個漂浮方陣的水下布置區域面積增大,在單個水域布置多個漂浮方陣時應計入該影響。
(3)在0°載荷方向角下,系泊間隔減小會造成相應比例的系泊纜張力增大,但在45°等斜向載荷下系泊纜張力增大比例大于0°載荷情況下的比例。在設計時應著重考慮載荷近端的系泊纜連接強度。
(4)本次研究作為大規模漂浮式光伏電站錨泊研究的首次嘗試,對相關工程應用提供了具有實踐性的研究思路和計算方案,同時也為后續的深入研究打下了基礎,后續可進一步研究系泊纜之間的干擾問題,以及某部分系泊纜破損狀態下的系泊響應情況。

