黃河三角洲地區港口全要素生產率的動態實證分析

梁文文，劉榮花，吳正

(1.山東省交通規劃設計院，山東 濟南 272008；2.河海大學 商學院，江蘇 南京 211100)

黃河三角洲(以下簡稱“黃三角”)作為我國最后的一個尚待開發的大河三角洲，國家高度重視其可持續發展形勢，并在各政策文件中明確提出要著重發展黃河三角洲高效生態經濟區，這也表明黃三角地區在山東省整體經濟發展中有著舉足輕重的作用。而濱州港、東營港、濰坊港和萊州港作為區域內主要港口，在黃三角經濟發展中的作用也極為重要，港口的高效發展也推動了黃三角區域外向型經濟的發展，提高了本區域的國際競爭力。山東省作為濱海大省，海洋經濟發展迅猛，港口資源優勢明顯。就港口資源而言，山東省港口自然地理條件相似程度較高，經濟腹地相互交叉，業務類型相似，導致同業競爭問題一直困擾著各港口的發展，而港口資源整合將是解決這一難題的主要辦法。港口資源整合的前提是深入了解各港口的發展狀況以及其競合關系，因此，對黃三角區域港口效率進行評價意義深遠。

有不少學者對港口效率評價問題進行了深入研究。Roll等[1]在評價港口效率時采用數據包絡分析(data envelopment analysis，DEA)模型；Tabernacle[2]通過研究碼頭集裝箱起重機作業的效率變化，分析了港口可移動集裝箱數量和裝卸時間的關系；Tongzon[3]將起重機數、泊位數、拖船數、堆場面積以及貨物吞吐量等作為指標對4個澳大利亞港口以及其他國際集裝箱港口的效率進行了對比研究。隨著理論的不斷發展，學術界將DEA方法和Malmquist指數相結合來評價港口的動態效率。龐瑞芝[4]在評價我國50家主要沿海港口經營效率的同時，分析了其動態效率；李蘭冰等[5]為了更有效地評價港口效率而進一步擴展了DEA模型；馬金鳳[6]使用DEA模型對長三角幾大港口進行定性分析，并對非有效的港口產生原因進行了解釋；滕煒超等[7]運用DEA法對港口進行有效性分析、規模收益分析、無效港口改進分析，并對各港口的競爭力進行排序；丁彩虹等[8]基于三階段DEA對江蘇省大型港口進行港口效率測度，認為長江經濟帶戰略有效促進了江蘇大型港口績效提升。這些學者的研究極大地提高了港口效率評價的有效性。在區域港口競合關系研究方面，相關學者也進行了研究。楊強等[9]在建立港口競爭力評價指標體系的基礎上，以環渤海地區港口為案例進行分析，并針對性地提出了破壞性創新合作戰略理論；孟慶春等[10]通過實證分析提出，青島港、大連港和天津港應建立新型的合作競爭關系，而不是一味維持傳統的對立競爭關系；張廣興等[11-12]在研究臨港產業與腹地產業共生關系的同時，進一步通過實證分析對冀東三港的經濟貢獻進行測算。已有研究多是對區域港口的有關指標進行比對或對港口間的競合關系展開討論，鮮有文獻對區域港口群的效率進行實證研究分析。山東省在進行港口資源整合時，首先要理清港口間的競合關系，確保資源整合后各港口可以協同發展。而港口的全要素生產率可以很好地表明港口的發展態勢，有利于管理者進行針對性的管理規劃。

基于此，本文運用DEA模型和Malmquist生產率模型，實證分析了2010年—2017年我國黃三角地區四大港口(濰坊港、東營港、濱州港和萊州港)的全要素生產率并得到動態效率，根據分析結果對區域港口提出具有針對性的政策建議，為保障山東省資源整合工作穩步進行，加快黃三角地區港航戰略聯盟的建設，促進區域經濟綠色發展提供科學依據。

1 模型設定及數據選取

1.1 模型設定

1.1.1 DEA模型

DEA作為一種非參數統計的方法，對多投入、多產出的若干決策單元(DMU)的相對有效性做出評價。Charnes等[13]在1978年提出了規模報酬不變的C2R模型。假定n個決策單元DMU，第j個DMUj(j=1,2,…,n)的輸入與輸出向量為xj=(x1j,x2j,…,xmj)T>0和yj=(y1j,y2j,…,ysj)T>0，輸入與輸出的權向量為v=(v1,v2,…,vm)T和u=(u1,u2,…,us)T，且v∈Em、u∈Es，E為單位向量，則DMUj的效率評價指數hj為式(1)。

(1)

此后，Banker等[14]拓展了C2R模型，提出規模報酬可變的BC2模型。用DEA模型對決策單元的相對效率進行評價時，可能產生多個DMU均是相對有效的情形，無法進一步對這些有效DMU進行比較與評價。為彌補這一缺陷，Andersen等[15]提出超效率DEA模型，該模型計算所得的效率值可大于1，從而實現對有效DMU相對效率的比較。

1.1.2 Malmquist生產率模型

Malmquist生產率指數由瑞典經濟學家Malmquist[16]最早提出，經Fare等[17]進一步發展，Malmquist指數定義如下：

(2)

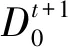
分解式(2)得式(3)。

=TE(yt+1,xt+1;yt,xt)×TP(yt+1,xt+1;yt,xt)，

(3)

其中，TE(yt+1,xt+1;yt,xt)表示技術效率，TP(yt+1,xt+1;yt,xt)表示技術進步。也就是說，公式(3)將全要素生產率分解為技術效率和技術進步。

若假設該等式規模報酬可變，則技術效率可進而分解成純技術效率與規模效率。因此可得：

MI(yt+1,xt+1;yt,xt)=PT×SE×TP，

(4)

當MI大于1時，表明全要素生產率增長；當技術效率(TE)或技術進步(TP)大于1時，表明TE或TP是全要素生產率提高的重要因素；反之，則是全要素生產率降低的主要動因。

1.2 數據選取及說明

基于數據的可得性，選取港口泊位數量、泊位長度、裝卸機械臺數、港口勞動力、港口的堆場面積和港口倉庫的總面積作為本文區域港口的投入型指標，然后選取港口貨物的吞吐量和港口集裝箱的吞吐量作為本文區域港口的產出型指標，并且以我國黃河三角洲區域的東營港、濱州港、濰坊港、萊州港等4個港口為決策單元，研究范圍為2010年—2017年，共計256個觀測值。樣本數據主要來源于2010年—2017年的《中國港口年鑒》[18]。

2 實證分析

2.1 黃三角地區各港口總體技術效率測算

本文將非徑向與超效率模型相結合，假設規模收益可變，以我國黃三角地區2010年—2017年四大港口選取的指標數據為樣本，運用MaxDEA5.2軟件，根據公式(1)測算4個港口的總體技術效率，結果如圖1所示。

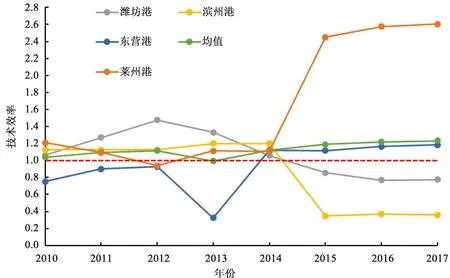
圖1 我國黃三角地區2010年—2017年四大港口的技術效率Fig.1 Technical efficiency of the four major ports in the Yellow River Delta region of China from 2010 to 2017

從技術效率變動角度，黃三角地區2010年—2016年主要港口總體技術效率呈現增長態勢，2010年黃三角地區主要港口技術效率總體均值為1.037，2017年上升至1.230。設定技術效率大于1的單元為有效單元，那么從有效單元角度來看，2010年有3個有效單元，以效率值高低排序依次為萊州港、濱州港和濰坊港；2011年有效單元個數未變，但港口相對有效性發生變化，濰坊港上升至第1位，萊州港下滑至第3位；2012年萊州港技術效率不佳，為無效單元；2013年萊州港技術效率上升，重回有效單元之列；2014年東營港進入有效單元，有效單元數量增加至4個；2015年萊州港、東營港技術效率上升，濰坊港、濱州港技術效率下降至無效；2016年萊州港和東營港技術效率持續上升，濰坊港、濱州港技術效率依然無效；2017年萊州港和東營港技術效率上升至2.605和1.183，較2010年的1.208和0.753，效率提升較為顯著。

結合實際情況可以知道，萊州港瀕臨煙臺港，受煙臺港輻射較大，所以其技術效率一直保持增長趨勢；東營港由于區位優勢明顯，資源豐富，所以其技術效率也在逐年增長；由于2015年濰坊港集團成立，集團對濰坊港進行港區投資建設，這一舉動影響了其技術效率，導致從2015年開始到2017年濰坊港的技術效率均為無效單元；濱州港2015年起規劃加快港區建設，這也導致從2015年開始到2017年該港的技術效率均為無效單元。

2.2 黃三角地區港口的動態效率測算

本文綜合運用DEA模型與Malmquist生產率模型，通過公式(3)和公式(4)測算我國黃三角地區主要港口的全要素生產率與技術效率的動態變化。

表2 我國黃三角地區2011年—2017年四大港口Malmquist生產率指數及其分解參數Table 2 Malmquist productivity index and its decomposition in the four ports of China's Yellow River Delta in 2011—2017

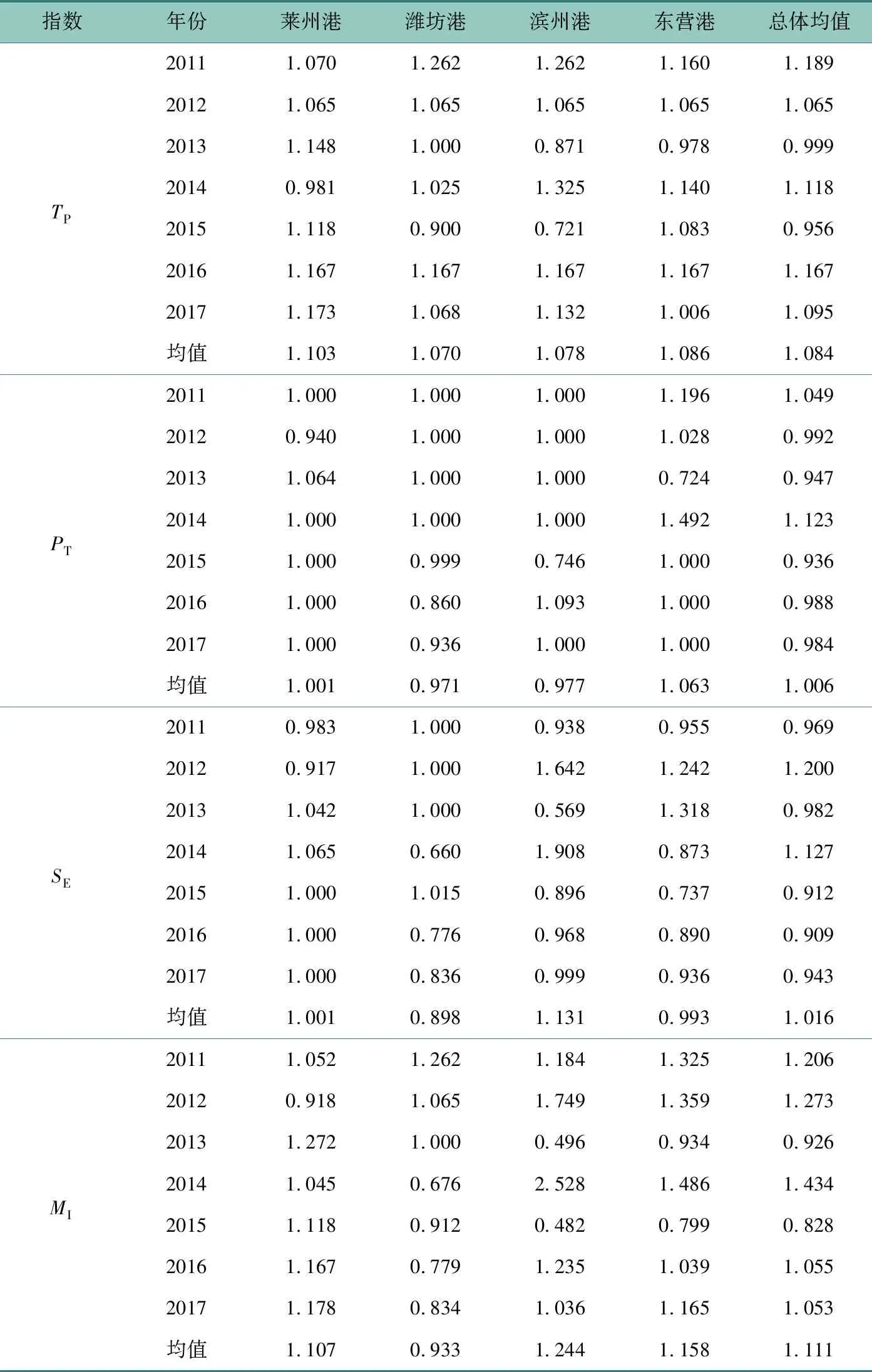
續表2

表2為我國黃三角地區2011年—2017年4個港口Malmquist生產率指數及其分解情況。從時間角度，2011年—2017年我國黃三角地區四大港口的技術效率整體呈現上升態勢，2011年—2017年Malmquist生產率指數總體均值為1.111。從樣本期間各港口Malmquist生產率均值角度，除濰坊港外，其他3個港口的MI年均值皆大于1，其中年均值最高的濱州港為1.244，而濰坊港的年均值最低為0.933。根據這個結果可以發現，我國黃三角地區各港口在2011年—2017年期間的Malmquist生產率存在的差距較為明顯。具體來看，萊州港、濱州港和東營港的Malmquist生產率指數都實現了較大幅度的增長，分別提高了9.5%、27.9%和15.7%。

從整體上看，技術效率(TE)與技術進步(TP)共同促進了我國黃三角地區4大港口的發展，但技術進步的貢獻高于技術效率。2011年—2017年黃三角地區四大港口的技術效率年均值為0.999，技術進步年均值為1.084，后者比前者高出超8%，由此可知，技術進步是黃三角地區港口Malmquist生產率變動的主要推動力。將技術效率分解為純技術效率(PT)與規模效率(SE)，通過對比可以發現，黃三角區域港口的規模效率均值為1.016，大于純技術效率均值(1.006)。因此，我國黃三角地區港口整體技術效率的變動主要來源于規模效率變動，這是因為山東省內逐步開始港口資源整合工作，港口資源歸一化使得港口規模逐步擴大，致使黃三角地區港口技術效率提升。近期，山東省資源整合工作取得了實質性進展，這也將進一步促進黃三角地區港口效率的提升，促進黃三角區域經濟的穩步發展。

3 結論與建議

本文綜合運用DEA模型和Malmquist生產率模型，測算了我國黃三角地區2011年—2017年四大港口的投入產出效率，研究結論如下：

(1)對各年效率從橫向角度來看，黃三角地區2010年—2017年主要港口總體技術效率呈現增長態勢。

(2)從動態效率角度，我國黃三角地區2011年—2017年主要港口全要素生產率變動呈現以下特征：四大港口整體Malmquist生產率年均增長12%，呈上升態勢；黃三角區域不同港口全要素生產率存在較大差距：濱州港全要素生產率增長率最高，為27.9%；東營港增長率次之，為15.7%；再次為萊州港，增長9.5%；而濰坊港Malmquist生產率指數最低，為負向增長。技術進步是黃三角地區港口效率提高的主要驅動力，而另一個推動黃三角地區港口全要素生產率進一步提高的重要因素為技術效率變動，尤其是規模效率的變動。

總體來說，我國黃三角地區港口群的總體效率與各港口效率水平均不是很高，為進一步提升該地區港口群效率、優化港口群整體功能，需進行相應的結構調整。具體建議如下：

(1)基于資源、區位、政策等因素，明晰各港口的特點，規范其主營業務，避免因區域港口內部無序的競爭而造成的區域整體經濟效率的損失，從而影響區域經濟的發展。此外還需推動港口技術創新，以技術進步促進港口效率的提升。

(2)加快適應港口資源一體化，加大港口聯盟合作，避免港口間惡意競爭導致的資源浪費。

(3)改善港口與腹地間的空間通達性，推進港腹產業演進模式轉變為成熟發展模式，實現港口與腹地的共生互動，實現港腹一體化發展。