增強物理建模能力,決勝2020年高考
梁金中
近年來,全國課標卷物理試題凸顯了“素養立意”的命題思想,對考生的學科素養要求較高,要求考生在面對實際問題時具有較強的物理建模能力,轉變“解題”為“解決問題”.在高中物理教學尤其是高三復習中,教師應著重加強學生的物理建模能力和應用物理模型解決問題能力的培養,使學生在面對復雜的物理問題時,能將其分解為若干個簡單問題,構建物理解題模型,熟練地根據物理模型特點巧選物理規律完成解答.本文以兩道全國高考題為例,談談如何培養學生的物理建模能力,歡迎指正.
1 高考對考生物理建模能力的要求
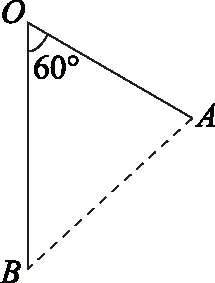
圖1

試題分析本題考查重力場、電場、平拋運動規律、動能定理等物理核心知識;涉及的物理過程主要有:1)在重力場中的平拋運動;2)帶電小球在重力場和電場的復合場中的類拋體運動.本題對學生學科素養要求較高,要求具備較強的分析綜合能力和應用數學知識處理物理問題的能力,要求學生對“質點”“點電荷”“復合場”“拋體運動或類拋體運動”等物理模型有深入的理解.試題的難度為 0.14.
本題第(1)問中涉及小球在重力場中的平拋運動,是學生比較熟悉的物理模型.而第(2)問的復合場中小球做的是類拋體運動,因沒有明確小球的初速度方向和勻強電場的方向,小球的運動軌跡難以描繪,學生難以應用拋體運動模型進行求解,思維陷入困境.應用功能關系解題,同樣需要學生有較強的數理建模能力和物理思維能力,解題過程較復雜,試題難度大.

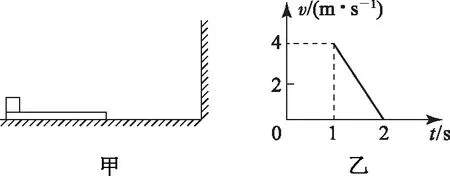
圖2
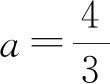
本題是高中常見的板塊問題,但因試題涉及長木板和小物塊的運動,屬于多物體、多過程、多狀態、多物理量的典型復雜物理問題,對思維水平和應用模型能力要求較高,且隱含條件不易發現,極易產生錯誤點.試題注重過程模型的識別及其銜接的關系分析.考生須對題中文字信息和圖象信息進行深入分析,針對每個過程正確選擇研究對象,建立恰當的物理模型,最終運用相關的物理概念和規律解決.
上述兩道試題都較好地體現了考試大綱所強調的“能夠獨立地對所遇到的問題進行分析、研究,弄清其中的物理狀態、物理過程和物理情境,找出起重要作用的因素及有關條件;能夠把一個復雜問題分解為若干較簡單的問題,找出它們之間的聯系;能夠提出解決問題的方法,運用物理知識綜合解決所遇到的問題”,體現高考要求學生具備較強的物理建模能力和應用模型解題的能力.
2 學生物理建模能力的培養
物理建模是物理學中的重要思想方法,是考生化解難題和解決物理問題的有效方法.高考一直將“是否能從實際物理問題中建立合理的物理模型”作為考查學生物理素養和物理能力的重點,因此,在物理教學中,必須增強學生建模意識,指導學生針對實際物理問題構建解題模型,提高應用物理模型解題的能力.
2.1 重視物理概念和規律,培養學生物理建模意識
物理現象和物理問題總是復雜多變的,為了便于問題的研究和解決,高中物理為學生提供了各種理想化的物理模型,形成了系統的物理知識和物理思維.理解和掌握這些物理知識和規律,就能夠在遇到實際物理問題時,根據問題的情境和給定條件,將問題轉化為一個個物理模型并解決問題.
高中物理模型包括對象模型、條件模型、運動模型、作用模型、守恒模型等.對象模型有質點、輕彈簧、輕繩、輕桿、單擺、點電荷、定值電阻、電容器、電感線圈、理想變壓器等;條件模型有光滑表面、勻強電場、勻強磁場等;運動模型有勻速直線運動、勻變速直線運動、自由落體運動、豎直上拋運動、平拋運動、勻速圓周運動、簡諧運動等;作用模型有萬有引力、重力、電場力、安培力、洛倫茲力、核力等;守恒模型有機械能守恒、動量守恒、質量守恒、電荷守恒等.
學生不僅要理解和掌握這些物理模型及其規律,還需要在解決實際問題的過程中具有良好的物理建模意識,主動尋找解決物理問題的最優模型,以達到高效解決問題的目的.如2014年課標卷Ⅰ第25題的標準答案是利用“功能關系和勻強電場模型”進行求解,實際上,也可利用“運動的合成與分解模型和牛頓第二定律”相結合進行求解,如果利用“力的合成與分解和動能定理模型”相結合進行求解,還會更簡潔.又如2015年課標卷Ⅰ第25題,在應用“勻變速直線運動模型”解題時,既可用勻變速運動的基本公式,也可用勻變速運動的推論和結論,靈活性很強,思維活躍的學生還可以選擇功能關系輔助求解.高考試題求解方法的多樣性和靈活性,給具有不同科學素養的學生提供寬廣的展示空間,讓學生系統掌握各種物理模型,是提高學生物理學科核心素養的重要教學目標.
2.2 加強教學的針對性,培養學生的物理建模能力
物理問題的解決總是依靠構建物理模型來實現,因此,高中物理教學中要重視培養學生的建模能力,使學生在面對物理問題時,懂得如何通過對問題情境的分析和判斷,忽略次要因素和無關因素,透過現象看清問題本質,科學構建解決物理問題的物理模型.
高三物理復習不應是物理知識的簡單再現,而是讓學生接觸更多的物理原始問題,學會分辨主要因素和次要因素,能根據問題的情境將復雜問題分解為若干小問題,將復雜的物理過程分解為若干簡單的子過程,再根據物理模型來解決每個小問題.如2015年全國課標卷Ⅰ第25題,就需要學生將長木板和小物塊的運動分解為8個子過程,并根據各子過程的物理模型特點進行求解.在物理教學中,教師要從解決問題的學科特點出發,不斷滲透物理模型,把物理建模始終貫穿于教學之中,通過潛移默化,不斷地引導學生進行科學觀察、科學分析,使其在解決問題時能優先考慮問題所屬的物理模型,然后通過物理模型的知識和規律解決問題,使建模和應用模型成為學生思考問題和解決問題的有效手段.
2.3 重視練、考、評相結合,增強學生的物理建模能力
物理建模并不是一個簡單的思維過程,學生除了要具備豐富和扎實的物理基礎知識外,還需通過適當的練、考、評,掌握一般問題的建模方法.物理問題通常可以通過分析綜合、聯想類比等方法進行建模.
分析與綜合,就是從全局到局部、整體到個體,再從局部到全局、個體到整體的思維過程.把復雜的物理過程按照時間順序或空間區域,分解為相互聯系的幾個子過程,認真分析和研究每個物體和各個子過程,在分析和綜合的基礎上,實現物理模型的建立.
聯想類比是指某些事物具有相似性特征或者某些方面相同時,推理它們在其他方面也可能相同的思維過程,從而應用較熟悉的模型、方法和規律去解決新問題.如用平拋運動的模型去解決電場中的類平拋運動問題,用天體運動模型去解決原子中的電子運動問題,等等.
物理學常見的建模方法還有對稱法、微元法、等效法等,這就要求教師在教學中加以引導和示范,通過講、練、考、評等多種形式,有計劃地設計各類典型原始物理問題,不斷創設問題情境,通過一題多解、一題多問和多題同解等多種形式,增強學生的物理建模能力,提高學生的物理學科核心素養.

