基于隱半馬爾可夫模型的補償電容維修機制優化

孫浩洋, 劉伯鴻

(蘭州交通大學自動化與電氣工程學院，蘭州，730070)

軌道電路作為鐵路信號傳輸系統的關鍵設備之一，其可靠性直接影響行車安全。補償電容在軌道電路系統中起到延長信號傳輸距離的作用[1]。鋼軌作為信號長距離傳輸的路徑，顯強感抗特性，可通過增設補償電容利用諧振的方式來抵消鋼軌的感抗。一般情況下，單個補償電容的故障不會造成軌道電路故障的發生，當多個補償電容故障時，會導致鋼軌感抗大大提高，進而誘發紅光帶現象[1]，由于在一個軌道區段內補償電容的數量較多，對發生故障的補償電容進行及時更換極為重要，若未及時發現補償電容的故障，當紅光帶現象發生時，所需更換的補償電容數量及位置均不好掌握，影響列車運行效率。

現階段微機監測系統實現了軌道電路各個設備運行數據的實時監測，文獻[1～2]通過分析鐵路信號的傳輸機制，對信號傳輸路徑進行建模，實現了以建模的方式進行軌道電路的故障預測；文獻[3]通過對軌道電路的傳輸機制進行可靠性分析，采用健康參數及隨機模糊理論對其剩余壽命進行估計；文獻[4]通過實驗室建立的四端口網絡結合單輪對占用方式模擬紅光帶，通過BP神經網絡結合故障樹的方式對軌道電路進行智能故障診斷；文獻[5]繪制了軌道電路信號傳輸路徑的可靠性框圖，結合共因失效模型和貝葉斯網絡安全分析模型對軌道電路的安全性和可靠性進行研究；以上研究均無法體現故障預測的實時性及補償電容故障精準定位。因此對補償電容故障的精準定位即實現單個補償電容剩余壽命的估計，進而優化其維修機制是亟待解決的問題。

本文提出了一種在鋼軌上增設傳感器監測其軌面電壓，利用傳輸路徑上不同部位上的軌面電壓的變化來縮小補償電容故障的范圍，進而實現精準定位。結合監測的各部位軌面電壓及道砟電阻，建立各補償電容故障的隱半馬爾可夫模型，對補償電容的全生命周期進行仿真建模，實現軌道電路補償電容的剩余壽命估計。

1 軌道電路補償電容采集電路

軌道電路是由多個電氣部件和一段鐵路線路的鋼軌構成的特種電路，其組成部件中既有集中參數電路也有分布參數電路。對集中參數電路即鋼軌傳輸線路部分可利用經典的KCL和KVL進行分析，結合電路理論中的二端口網絡理論，即可建立軌道電路等效的二端口傳輸路徑模型，實現對軌道電路傳輸路徑可靠性的分析[2]。

根據軌道電路調整表，以1 700 Hz、900～1 000 m的軌道區段為例，采用分段的四點式對主軌道區段的軌面電壓及軌入軌出電壓進行實時監測。軌道電路等效電路及增設的軌道電路采集點見圖1。

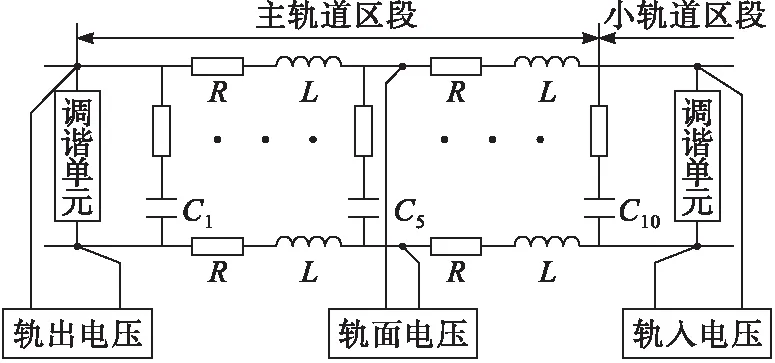
圖1 軌面電壓采集等效電路圖

當前研究背景下的ZPW-2000A軌道電路微機監測系統對于補償電容的監測數據主要反映在主軌道的軌入電壓和軌出電壓[2]，由于軌道電路長度較大且補償電容設置數目多，僅通過軌入及軌出電壓反映整段軌道電路補償電容的工作狀態略有欠缺，本文提出在主軌道傳輸路徑中增設2個軌面電壓采集點，通過軌面電壓采集點與軌入電壓、軌出電壓共同完成對軌道電路補償電容剩余壽命的估計，進而優化補償電容的維修機制。

2 補償電容監測數據分析

根據軌道電路的傳輸機制及鋼軌的感抗特性進行傳輸路徑的二端口網絡的建模，并與實際數據進行對比，驗證仿真模型的有效性與準確性。

在調整狀態下，補償電容無故障時，軌入、軌出端接收到的電壓幅值近似為定值，故信號集中采集的移頻主軌接收電壓曲線為一條直線。補償電容故障對軌入、軌出電壓影響的實際數據見表1[2]。補償電容故障對主軌中心及小軌中心電壓的影響見表2[2]。

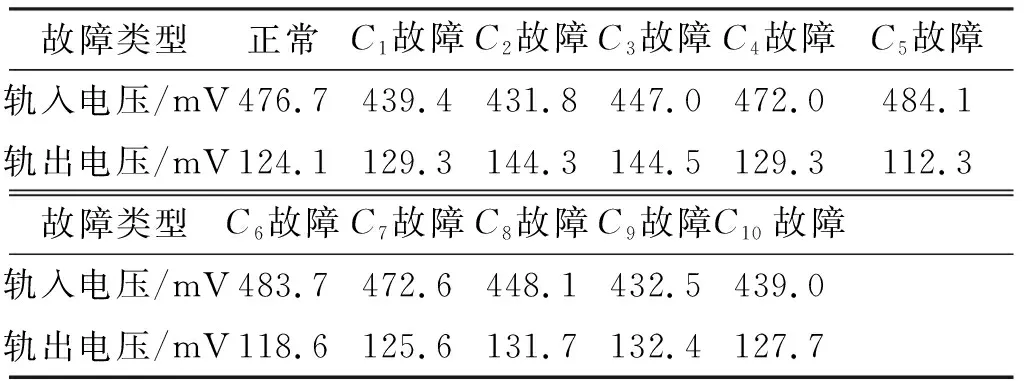
表1 補償電容故障對軌入軌出電壓的影響

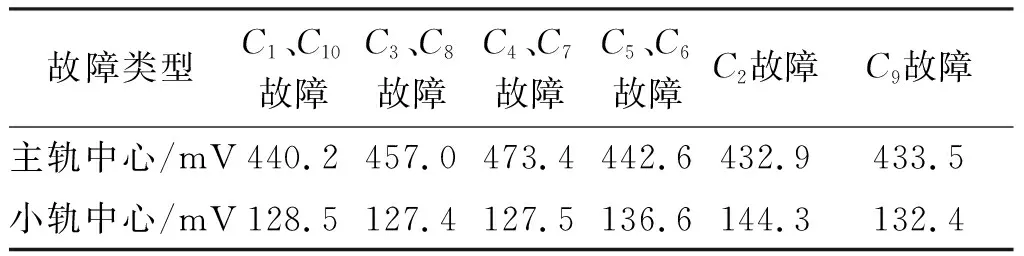
表2 補償電容故障對主軌小軌中心電壓的影響

根據表1、表2不同部位的補償電容發生故障時，對軌入、軌出電壓、主軌中心及小軌中心電壓會產生不同的影響，可以采取增加監測點的方式進行特征數據提取提高補償電容故障預測及剩余壽命估計的精確度。

3 補償電容剩余壽命估計

3.1 補償電容隱半馬爾可夫模型建立

通過HSMM(Hidden Semi-Markov Model，HSMM)結合補償電容的故障特性：軌道電路為電氣化設備，其兩端的電壓即可反映其工作狀態是否正常[3]；現階段微機監測系統可提供連續的軌道電路補償電容的工作電壓[4]；通過HSMM的狀態駐留時間參數可對補償電容的剩余壽命進行估計、并可以預測其發生泄漏及容值低于額定值的時間[5-7]。

狀態個數：N，即補償電容從正常態到故障共經歷N個退化狀態S1、S2、S3、S4，再此根據補償電容的故障特性及其容值發生泄漏的狀態將其退化狀態分為4步。

觀測值個數：M，即補償電容工作狀態所對應的監測電壓值的數目，根據補償電容由工作初始、泄漏狀態、故障狀態將補償電容的全生命周期進行劃分。

初始概率分布矢量：π=(π1，π2，…，πN)，即補償電容工作的初始狀態處于某一階段的概率分布，πi=Pr(q1=θi),1≤i≤N。

狀態轉移矩陣：A={aij}，即補償電容工作狀態轉移矩陣，aij=Pr(qt+1=j|qt=i),1≤i,j≤N。

輸出概率矩陣：B={bj(o),j=1,2,…,N},對于連續HSMM，B是一組觀測值概率函數，用以表示每個特征值處于哪種全生命周期狀態的概率，在此用高斯混合參數進行描述:

(1)

式中：M={Mj}代表混合高斯元的個數；c={cjl}代表混合高斯元的權重；μ={μjl}代表均值向量；U={Ujl}代表協方差矩陣。其中1≤j≤N。

混合系數矩陣:

(2)

假定補償電容觀測值維度為d,cjl為狀態Sj的第1個混合參數，滿足約束：

(3)

均值矩陣:

(4)

協方差矩陣:

(5)

式中：Ujl是一個d維方陣，表示狀態Sj的第1個高斯分布的協方差矩陣。

綜上所述，狀態補償電容的Sj其概率密度函數可表示為：

(6)

其中：

(7)

狀態駐留時間分布矩陣：P={Pi(d)}表示每個狀態的概率分布。Pi(d)=P(d|qt=i),1≤i≤N，1≤d≤D。D為全生命周期模型中每種狀態的持續時長，通過其分布得出駐留時間的方差及均值。

綜上所述，連續性HSMM可表示為：λ=(N,M,π,A,B,P)，其中B=(c,μ,U)。對HSMM模型的訓練過程就是對λ各項參數進行賦值的過程。

3.2 補償電容HSMM剩余壽命估計

基于HSMM的剩余壽命估計方法這一階段主要用到HSMM中狀態駐留時間參數，根據補償電容全壽命周期劃分的4種狀態結合各個狀態的駐留時間，計算其剩余壽命[8-10]。狀態轉移示意圖見圖2。

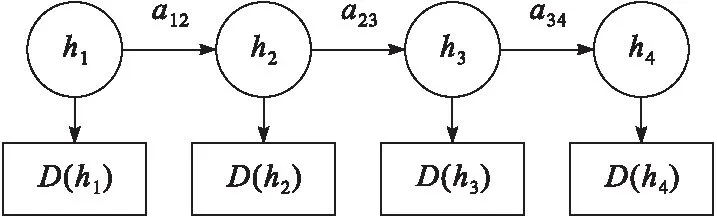
圖2 狀態轉移示意圖

首先按照均勻分布對Pi(d)進行初值估計，采用Viterbi算法對特征值描繪的狀態路徑確定對應的均值μ和標準差σ，然后計算每個狀態的最大駐留時間。

D(hi)=μ(hi)+pσ2(hi)

(8)

(9)

(10)

式中：T為所有的觀測值個數。補償電容剩余壽命計算方法見圖3。

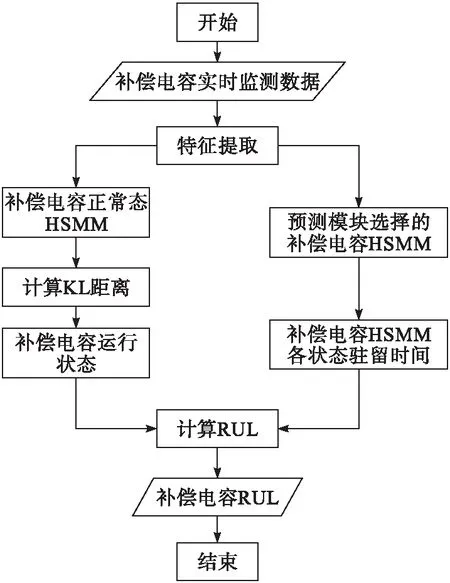
圖3 補償電容剩余壽命計算方法

在完成對全周期模型的訓練后將當前采集的數據與多個預測模型相匹配，通過與當前監測數據匹配度最高的模型進行補償電容3個參數的計算：補償電容剩余壽命上限、均值及下限[11-12]。

(11)

(12)

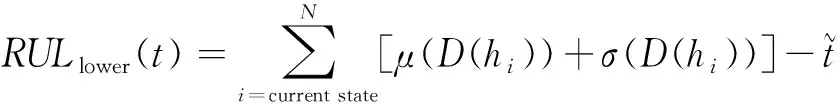
(13)

因此利用此方法可以隨著補償電容的工作時間對其進行實時監測，每得到一個觀測值，就可以根據全生命周期HSMM進行剩余壽命估計，繪制出實際的退化模式曲線。

(14)

4 基于KL距離的健康評估總體思路

4.1 退化模式識別

在退化狀態識別階段，利用Viterbi算法的性質，結合補償電容全生命周期模型和概率計算理論等直接對歸一化后的補償電容分路電流進行狀態識別，判斷其所屬的全生命周期階段[13-15]。補償電容全生命周期退化狀態識別方法圖4。

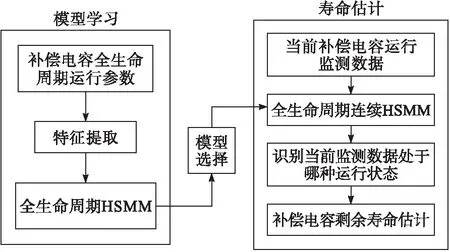
圖4 退化狀態識別方法

如圖4所示，利用多個補償電容的全壽命周期歷史運行數據建立多個連續的HSMM。利用Viterbi算法進行補償電容當前運行狀態的識別。

將補償電容的全生命周期劃分為4個退化狀態，分別為正常狀態、輕微退化狀態、性能不良狀態及故障狀態，按照補償電容的容值及其額定工作容值進行狀態劃分，補償電容的容值可通過監測電壓直接反映，補償電容退化狀態劃分情況見圖5。

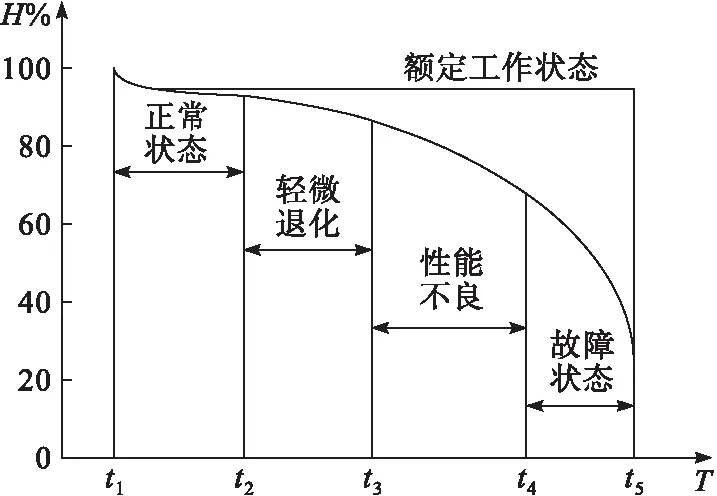
圖5 補償電容退化狀態劃分情況

根據圖5通過健康評估思想，結合補償電容的工作電壓偏移額定值的距離對其工作狀態進行劃分。依據訓練后正常態的HSMM求得P正常(O|λ)，然后結合電路當前狀態經正常態HSMM得到對應的P未知(O′|λ)，通過[P正常(O|λ),P未知(O′|λ)]計算出KL距離。

4.2 KL距離定義

KL距離的大小即為當前運行參數偏離正常態的程度，KL值越小則補償電容工作越接近正常狀態，KL值增大，補償電容工作的可靠性也隨著降低[16-18]，若偏移的KL距離大于閾值(即補償電容的歸一化分路電流超出額定值)，則補償電容失效。KL距離定義為:

dKL[P未知(O′|λ)||P正常(O|λ)]=

(15)

5 仿真試驗

5.1 仿真試驗指標

利用補償電容泄漏狀態數據對HSMM進行訓練，通過全生命周期模型及狀態駐留時間，估計補償電容的壽命。通過調整二端口網絡傳輸路徑，模擬各個補償電容泄漏情況，驗證HSMM在補償電容剩余壽命估計方面的精確度。由于補償電容實際工作壽命受溫度影響較大，而驗證模型的有效性和可靠性無需考慮溫度對其的干擾，只需驗證該模型能否對補償電容的剩余壽命進行準確的預估。

現將補償電容容值泄漏至其額定值的60%為失效狀態進行仿真試驗[19-21]，以勻速降低補償電容容值直至低于補償電容額定容值的60%所需的時間即為實際剩余壽命，通過HSMM結合補償電容監測點采集的分路電流對補償電容的剩余壽命進行估計，通過對比二者之間的差距來判斷該方法的有效性。

5.2 補償電容泄漏定位原理

當單個補償電容發生容值泄漏而導致的電容幅值不斷降低時，根據全生命周期的退化路徑對其進行劃分，補償電容處于退化初期和中期，接收端主軌出及其余各個監測點的歸一化分路電流如下。

下面以主軌C4處補償電容故障為例。補償電容正常工作時，接收端所接收到的補償電容泄漏時的軌出電壓監測點的歸一化分路電流見圖6。

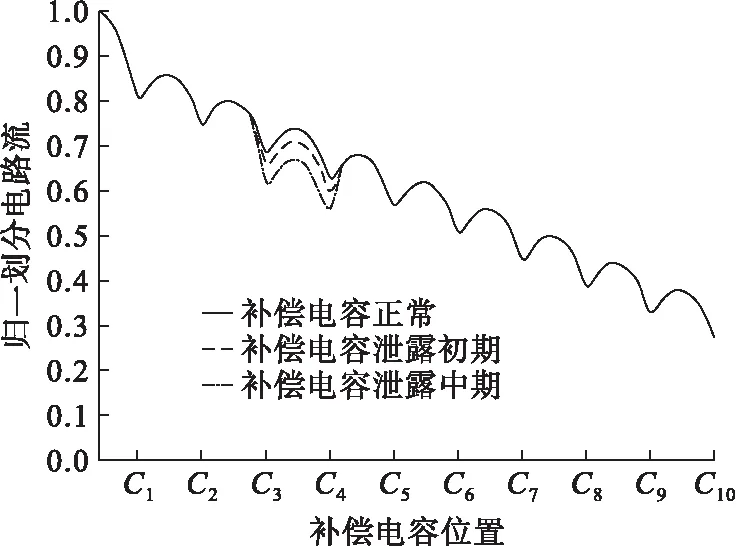
圖6 補償電容泄漏時的軌出電壓監測點分路電流

圖6中，當補償電容發生泄漏時，隨著時間的推移，補償電容容值不斷降低，無法平衡鋼軌的感抗，由于在進行補償電容剩余壽命估計時假設道砟電阻不變，鋼軌感抗增加，軌面電壓和分路電流均減小。由于軌出電壓監測點與補償電容C1的距離最近，傳輸路徑最短，信號衰減的程度最低，故C1處的軌面電壓和分路電流最大，隨著傳輸路徑的增長，軌面電壓和分路電流隨之減小。接收到的補償電容泄漏時的監測點1分路電流見圖7。

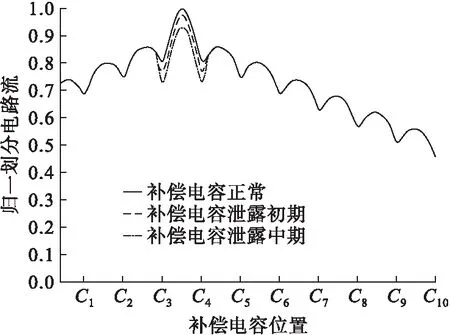
圖7 補償電容泄漏時的監測點1分路電流

圖7中，由于軌出電壓監測點與補償電容C3及C4的距離最近，傳輸路徑最短，信號衰減的程度最低，故C3、C4處的軌面電壓和分路電流最大。接收到的補償電容泄漏時的監測點2分路電流見圖8。

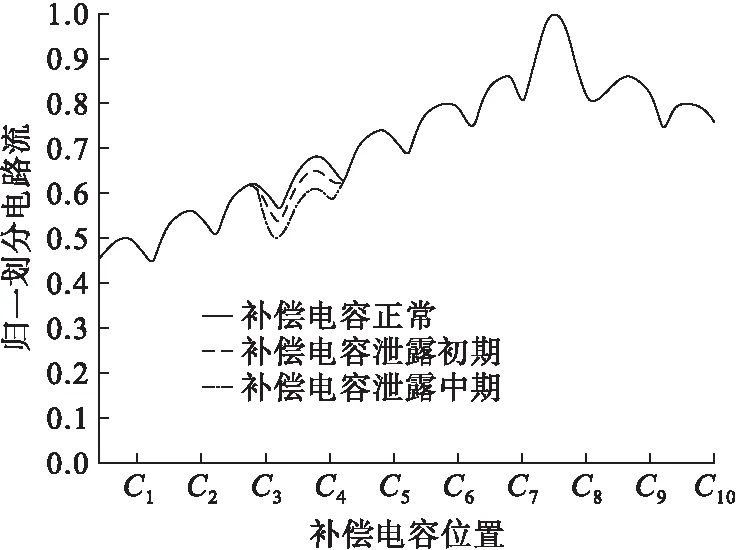
圖8 補償電容泄漏時的監測點2分路電流

如圖8所示，由于軌出電壓監測點與補償電容C7及C8的距離最近，傳輸路徑最短，信號衰減的程度最低，故C7、C8處的軌面電壓和分路電流最大。由于C4補償電容發生泄漏，隨著時間的推移其C4處的分路電流不斷減小。

通過對各個監測點監測的補償電容分路電流進行歸一化處理，得到由于C4補償電容故障的各個監測點歸一化分路電流，并可實現補償電容故障的精準定位，進而實現補償電容維護操作的優化。

5.3 仿真試驗數據對比分析

通過勻速降低補償電容容值直至低于額定值的60%所需時間即實際剩余壽命，將其與HSMM預估的補償電容剩余壽命進行對比。采用軌出電壓和增設的軌面采集點1所采集的數據進行剩余壽命估計，實際剩余壽命與HSMM預計的剩余壽命對比見表3。

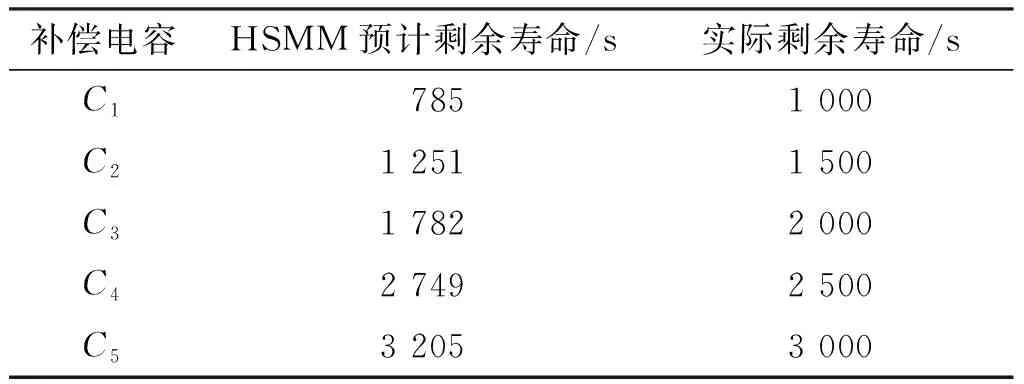
表3 增設補償電容軌面采集點1

采用軌出電壓和增設的軌面采集點2所采集的數據進行剩余壽命估計，實際剩余壽命與HSMM預計的剩余壽命對比見表4。

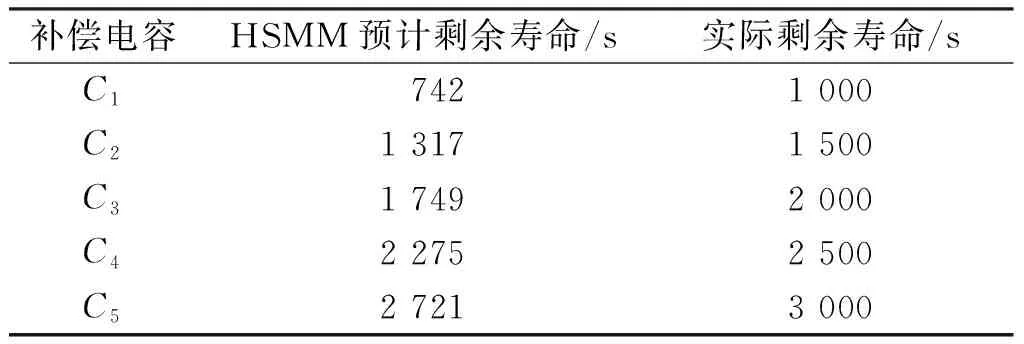
表4 增設補償電容軌面采集點2

采用軌出電壓和增設的軌面采集點1、2所采集的數據進行剩余壽命估計，實際的剩余壽命HSMM預計的剩余壽命對比見表5。

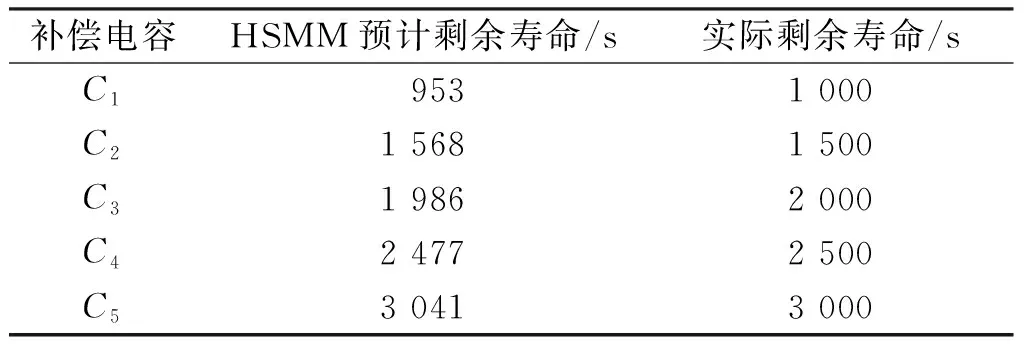
表5 增設補償電容軌面采集點1、2

通過對比表3～5可見，同時增設補償電容軌面采集點1和2后，剩余壽命估計的精確度較增設單個采集點有較大的提高，驗證了本文提出的增設采集點進行補償電容剩余壽命估計的精確度有較大的提升。

6 結論

現階段軌道電路在我國鐵路信號傳輸系統中實現了對列車運行追蹤與定位的功能，由于軌道電路傳輸距離長，補償電容數目多，無法實現故障的精準定位，影響檢修效率并大大增加了現場維修人員的工作量。本文主要工作及結果如下：

1)通過增設軌道電路軌面監測點的方式對補償電容的工作情況進行數據采集；

2)通過增設的補償電容采集點實現軌道電路補償電容故障的精確定位；

3)根據軌道電路仿真模型數據訓練其全生命周期HSMM，通過增設的補償電容采集點及其全生命周期HSMM實現了對補償電容剩余壽命的估計；

4)通過對補償電容全生命周期進行劃分，對即將發生故障的補償電容進行精確定位，實現從故障修到狀態修的轉化，不僅降低了現場操作人員的工作量，而且實現了全方位的補償電容工作狀態實時監測。