峰均比約束下機載MIMO雷達頻譜共存波形設計

童日武， 張劍云， 周青松

(國防科技大學電子對抗學院， 合肥， 230037)

近年來，隨著無線通信技術的快速發展特別是5G時代的到來，頻譜帶寬的需求量日益增加，如何實現雷達和無線通信設備之間的頻譜共存問題受到了越來越多研究者的關注，而通過波形設計的方法可以有效實現頻譜共存，因此雷達和無線通信系統之間的頻譜共存波形設計成為了研究熱點問題[1]。

目前的研究文獻主要是從雷達角度出發，通過波形設計的方法實現與通信系統的頻譜共存。頻譜共存波形設計問題主要可分為如下2大類：第1類是在非雜波環境下的頻譜共存波形設計[2-7]。其中文獻[6]研究了在能量約束和相似性約束下的頻譜共享波形設計問題，并通過求解半正定規劃(Semi-Definite Programming，SDP)問題和使用秩-分解定理合成優化波形。文獻[7]通過對多共存頻帶局部設計，能夠精確控制每個頻帶的干擾能量。

第2類是考慮在雜波環境下的頻譜共存波形設計，以最大化信干噪比(Signal to Interference plus Noise Ratio，SINR)為設計指標。當前研究文獻[8-9]大多只考慮了波形的能量約束和相似性約束，沒有對波形的幅度加以約束，而在實際應用中為了能夠充分利用發射機發射功率，往往需要發射波形具有恒模或者較低的峰均比特性，因此對波形施加低峰均比約束是十分必要和有意義的。另外上述文獻都是先求解SDP問題，再通過秩-分解定理合成優化波形。然而求解SDP問題的運算復雜度較高，秩-分解雖然可以獲得高度近似解，但是只適用于能量約束和相似性約束下的全局頻譜波形設計，當同時施加峰均比約束或者局部頻譜設計時將不再適用，因此需要尋找新的有效算法求解本文的優化問題。

針對以上問題，本文在現有文獻的基礎上對波形進一步施加了峰均比約束，并分別研究了全局頻譜設計和局部頻譜設計這2種不同的設計方法。針對非凸聯合優化問題，本文提出了一種新穎的循環迭代算法，在每次迭代過程中將非凸優化問題轉化為可解的凸優化問題，再使用可行點追蹤連續凸近似(Feasible Point Pursuit Successive Convex Approximation，FPP-SCA)算法[10]直接求出波形的優化解。仿真結果表明了所提算法比現有算法具有更低的運算復雜度，且在施加峰均比約束條件時，無論是全局頻譜設計還是局部頻譜設計，都具有很好的適用性和靈活性。

1 信號模型

考慮集中式機載MIMO雷達，具有NT個發射陣元和NR個接收陣元。雷達平臺勻速直線運動，速度為v，無偏航。在一個相干處理間隔內發射M組脈沖信號，脈沖重復周期為恒定值T，波長為λ，其發射波形矩陣為ST∈NT×L，L表示每個陣元發射波形的采樣點個數。

當目標距離雷達很遠時，俯仰角可以忽略不計。則對于方位角為θ0的目標而言，其對應第m個脈沖m=(1,2,…,M)的接收信號在接收端經過下變頻和基帶采樣后可表示為：

(1)

式中：at(θ)∈NT×1和ar(θ)∈NR×1分別表示發射空間導向矢量和接收空間導向矢量，對于發射和接收陣元間距均為半波長的均勻線陣而言：

(2)

(3)

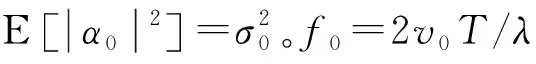
將Yt,m向量化，則有：

(4)

式中：

(5)

式中：IL為L×L的單位陣；s=vec(S)；?為克羅內克積。

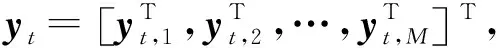
(6)

式中：

(7)

式中：p(f0)=[1,ej2πf0,…,ej2π(M-1)f0]T表示歸一化多普勒頻率為f0的時間導向矢量。為方便起見，使用A0來表示A(f0,θ0)。

對于雜波信號，如圖1所示，將雜波分為2R+1個等距離環，每個距離環分為Nc個雜波塊，雜波信號可表示為所有雜波塊信號的疊加[9]。

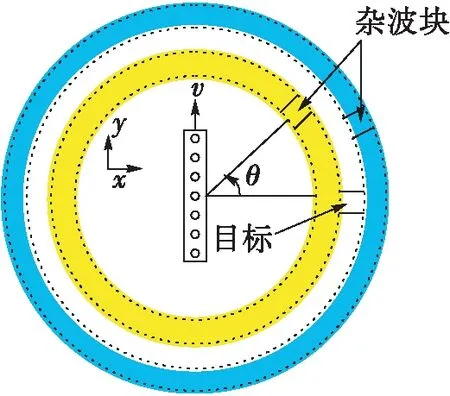
圖1 雜波距離環

類似于目標信號，位于第r(r=0,±1,…,±R,r=0表示目標所在距離環；r>0表示目標后面距離環；r<0表示目標前面距離環)個距離環中的第k(k=1,2,…,Nc)個雜波塊的回波信號表示為：

αc,r,kA(r,fc,r,k,θc,r,k)s

(8)

式中：

(9)

為方便起見，將A(r,fc,r,k,θc,r,k)表示成Ac,r,k。

Jr∈L×L表示轉移矩陣[11]，定義如下：

(10)

則雜波信號可表示為：

(11)

雷達接收機接收到的總信號為目標信號、雜波信號以及內部噪聲之和，表示為：

(12)

2 問題闡述

2.1 最大化輸出SINR

接收信號y通過有限長線性接收濾波器w后，輸出信號表示為：

yout=wHy=

(13)

故輸出SINR表示為：

SINR(w,s)=

(14)

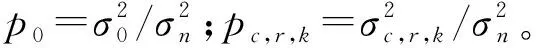
進一步有：

(15)

(16)

(17)

式中：

Rcns(s)=Rcs(s)+INRLM

(18)

(19)

Rcnw(w)=Rcw(w)+wHwINTL

(20)

(21)

2.2 頻譜兼容性約束

假設有K個與機載MIMO雷達系統共存的許可頻帶，第k(k=1,2,…,K)個頻帶范圍為[fk,1,fk,2]，則頻譜共存矩陣[6]表示為：

(22)

式中：ωk為第k個頻帶的權重；Rk為第k個頻帶的共存矩陣，表示為：

(23)

第n(n=1,2,…,NT)個發射陣元所發射的波形sn表示為：

sn=(IL?un)s=Uns

(24)

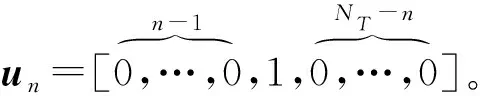
則MIMO雷達頻譜兼容性約束表示為：

(25)

式中：EI表示所有頻帶的最大允許干擾總能量。

以上只考慮了全局頻譜約束，只能保證所約束頻帶上總的能量低于設定門限值，但不能分別對每個頻帶上能量進行精確控制，在實際應用場景中，由于軍事、航海等活動的原因，往往某些特定頻帶比其他頻帶的優先級更高，且需要精確控制這些頻帶的允許干擾能量，這樣則需要對每個頻帶單獨施加頻譜能量約束。

局部頻譜約束表達式如下：

(26)

局部頻譜約束和全局頻譜約束之間的關系如下：

(27)

式(26)進一步又可表示為：

(28)

2.3 峰均比約束和相似性約束

發射波形往往能量恒定，本文假設波形具有歸一化能量，即sHs=1。

峰均比約束比恒模約束條件更為寬松，低峰均比約束既能保證充分利用發射機功率又能進一步提高SINR，其表達式如下[12]：

(29)

當ζ=NTL時，退化為能量約束。當ζ=1時則為恒模約束。

式(29)進一步可表示為：

(30)

Φi定義如下：

(m,n)∈{1,2,…,NTL}2

(31)

為了得到良好的波形特性，這里同時對波形施加相似性約束[6]：

‖s-s0‖2≤ε

(32)

式中：s0表示參考波形；ε(0≤ε≤2)表示相似度。

由上目標函數和約束條件可得全局頻譜設計時優化問題如下：

局部頻譜設計時優化問題如下：

3 優化算法

本節以全局頻譜設計時的優化問題為例提出具體的求解算法，局部頻譜設計時的優化問題可用同樣方法求解。

當固定s時，忽略常數項后可得如下無約束優化問題：

(35)

其閉式解為[13]：

(36)

式中：υ(·)表示矩陣最大特征值對應的特征向量。

當固定w時，問題(33)等價于如下優化問題：

進一步可得：

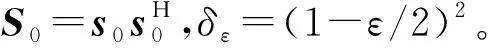
針對非凸優化問題(38)，本文通過以下方法進行解決。首先利用Charnes-Cooper變換[9]，問題(38)等價于如下優化問題：

觀察可發現，問題(39)中的目標函數是一個凸函數。但約束條件中的sHR0w(w)s=1，sHs=t以及sHS0s≥tδε并非凸集，下面將其進行凸近似處理。

sHR0w(w)s=1和sHs=t等價于如下不等式約束：

(40)

則問題(39)可轉化為如下優化問題：

t1,t2,t3為輔助變量，u為懲罰項參數，用來平衡原目標函數和輔助懲罰項。當t1,t2,t3等于0時，問題(41)的解同樣為問題(39)的解[10]。

觀察可發現sHR0w(w)s≤1+t1是一個凸集，對于sHR0w(w)s≥1-t1又可作如下凸近似處理。

因為R0w(w)是一個半正定矩陣，故對于任意z(z為復向量且與s維度相同)，一定有：

(s-z)HR0w(w)(s-z)≥0

(42)

展開可得：

sHR0w(w)s+zHR0w(w)z-2Re(zHR0w(w)s)≥0

(43)

利用式(43)替換約束條件sHR0w(w)s≥1-t1可得：

2Re(zHR0w(w)s)-zHR0w(w)z≥1-t1

(44)

此時式(44)為凸集。

同理約束條件sHs≥t-t2和sHS0s≥tδε-t3可經過凸近似處理為：

(45)

則問題(41)轉化成如下可解的凸的二次約束二次規劃問題：

優化問題(46)可通過文獻[10]中FPP-SCA算法求解，在第k次迭代中，令zk=sk-1，則需要求解如下優化問題：

本文所提算法的具體步驟如下：

輸入：參考波形s0，懲罰項參數u，退出條件ξ和η。

輸出：優化解sopt，wopt。

步驟1l=1，初始化波形s1=s0，更新R0s(s)和Rcns(s)，根據式求解w1，根據式求SINR1。

步驟2l=l+1

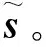
3)根據步驟1求解wl，SINRl。

步驟3重復步驟2，直到|SINRl-SINRl-1|≤η停止。

步驟4輸出sopt=sl，wopt=wl。

至于運算復雜度，在每次迭代過程中使用本文算法求解s時相當于求解一個二階錐規劃(Second-Order Cone Programming，SOCP)問題，其運算復雜度上界(最差情況下)為O((NTL)3.5)，而在文獻[9]中使用半正定松弛方法求解SDP問題的運算復雜度為O((NTL)6.5)，再通過秩-分解恢復波形的運算復雜度為O((NTL)3)。通過上述分析可以看出本文算法具有更低的運算復雜度。

4 仿真分析

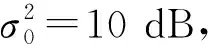
對于參考波形，由于線性調頻(Liner Frequency Modulation，LFM)信號具有良好的脈沖壓縮特性和模糊度，故本文使用正交線性調頻信號作為參考波形SLFM∈NT×L，其第(m,n)個元素的數學表達式如下：

SLFM(m,n)=

(48)

式中：m=1,2，…，NT；n=1,2,…,L；s0=vec(SLFM)。

4.1 能量約束下本文算法和文獻[9]中算法性能比較

本部分比較了本文算法和文獻[9]中算法在解決能量約束下的全局頻譜設計問題時的性能。E1=E2=0.000 1，ω1=ω2=1，相似性約束ε=0.3。為了公平比較，避免約束條件對運算復雜度的增加，在使用本文算法時同樣施加能量約束，但不施加峰均比約束。文獻[9]中的算法4通過求解SDP問題，再使用秩-分解定理恢復出優化波形。

表1給出了在碼長L取不同值時2種算法的CPU運行時間。從表中可以看出無論L取何值，本文算法都比對比算法具有更少的運算時間，并且隨著L取值的增大，2種算法運算時間的差距越來越大。當L=250時，對比算法顯示“內存不足”，即“N/A”，而本文算法仍然可以運行。以上說明了本文算法比對比算法具有更低的運算復雜度。

表1 2種算法CPU運行時間比較 s

表2給出了L=100時2種算法的仿真數據，可見本文算法和對比算法結果幾乎相同。圖2給出了2種算法的脈沖壓縮圖，圖中2種算法圖示幾乎完全重合。

表2 L=100時2種算法性能比較

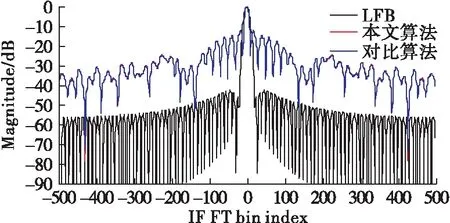
圖2L=100時2種算法脈沖壓縮圖

以上結果充分說明了本文算法在解決能量約束下的全局頻譜設計時能達到和對比算法同樣的效果。但更重要的是，本文算法具有更低的運算復雜度以及更強的靈活性和適用性，能夠解決峰均比約束下的波形設計以及局部頻譜設計問題，而對比算法只適用于能量約束下的全局頻譜設計問題。

4.2 不同峰均比約束下的全局頻譜波形設計

E1=E2=0.000 1，ω1=ω2=1，相似性約束ε=0.3。設置ζ=200,1.5,1，由式(29)中定義可知，ζ=200表示能量約束，ζ=1.5表示低峰均比約束，ζ=1表示恒模約束。

圖3給出了在不同峰均比約束下的SINR隨迭代次數的變化曲線，從圖中可以看出在未波形設計(即使用參考波形s0作為發射波形，對應圖中第1次迭代)時的SINR值為6.587 6 dB，而通過波形設計后SINR都存在明顯提升，當ζ=200時SINR為9.133 6 dB，當ζ=1.5時SINR為9.014 8 dB，當ζ=1時SINR為8.360 7 dB。另外可以看出在能量約束時SINR最大，隨著ζ的減小SINR也相應越來越小，當恒模約束時SINR值最小。這一結果符合理論預期，因為ζ的減小意味著波形幅度的自由度越來越小，從而導致SINR的下降。但從圖中同時可以看出，在低峰均比約束下，相對于能量約束而言SINR的損失程度較小，因此在波形設計時設置低峰均比約束是可以接受的。

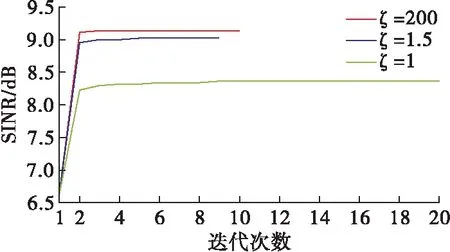
圖3 不同峰均比約束下的SINR變化曲線

圖4給出了在不同峰均比約束下的波形能量譜密度(Energy Spectral Density，ESD)，圖中同時給出了LFM信號的ESD作為參考。從圖中可以看出優化后的波形在相應頻帶上形成能量凹槽(如圖中陰影部分區域)，說明了所提算法能夠起到頻譜約束的作用，能夠實現頻譜共存。

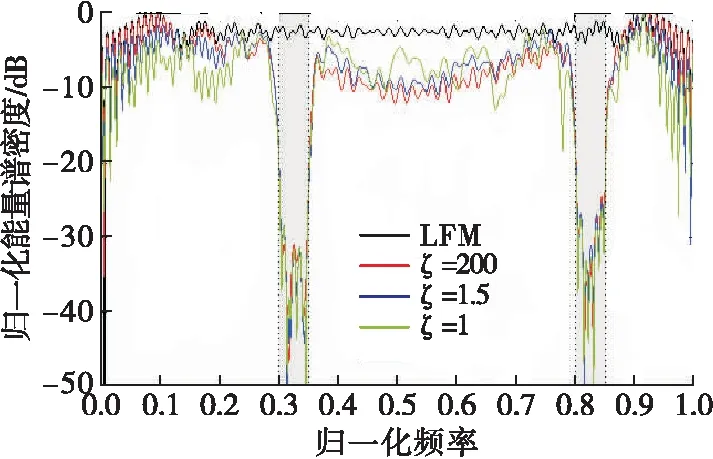
圖4 不同峰均比約束下的波形能量譜密度圖

圖5給出了不同峰均比約束下的波形幅度變化情況。從圖中可以看出在能量約束時波形幅度變化最大，隨著ζ的減小，波形幅度變化范圍越來越小，且不會超過峰均比約束幅度上界，當ζ=1時波形幅度恒定，此時為恒模波形。從以上結果可以說明本文所提算法很好地起到峰均比約束的效果。

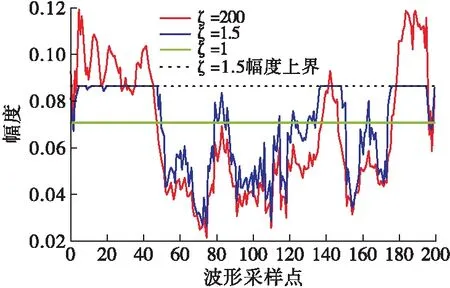
圖5 不同峰均比約束下的波形幅度變化曲線

4.3 不同相似性約束下的全局頻譜波形設計

E1=E2=0.000 1，ω1=ω2=1，峰均比約束ζ=1.5。設置相似性約束ε=2,0.3,0.1。

圖6給出了在不同相似性約束下的SINR變化情況。從圖中可以看出波形優化后SINR都存在明顯提升，但在ε=2時SINR值最大，為9.571 7 dB，隨著ε的不斷減小，SINR值不斷下降，當ε=0.1時，為7.376 7 dB。這一結果同樣是符合理論預期的，因為ε的減小同樣意味著波形的可行集在減小，從而導致了優化波形的自由度降低。

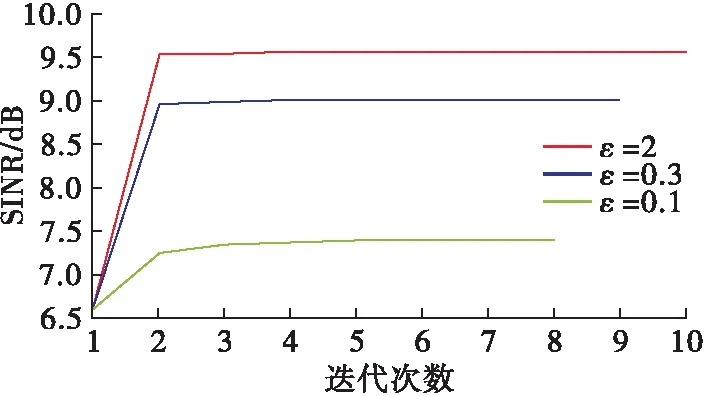
圖6 不同相似性約束下的SINR變化曲線

圖7給出了在不同相似性約束下的波形ESD。從圖中可以看出無論ε取值多少，優化后的波形都能在相應頻帶形成能量凹槽。但同時可以發現當ε=2時，波形的ESD在其他某些頻帶上的分布與LFM信號差異較大，而ε=0.1時則與LFM信號分布情況非常接近，這也說明了本文算法起到了相似性約束的作用。

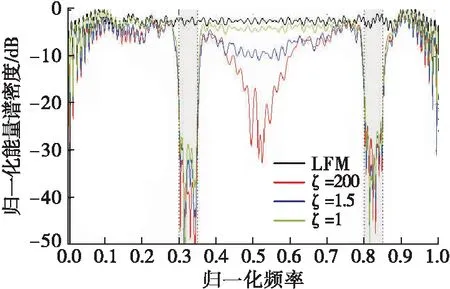
圖7 不同相似性約束下的波形能量譜密度圖

圖8給出了在不同相似性約束下的波形脈沖壓縮情況，脈壓經過加海明窗處理[14]，圖中同時給出了LFM信號的脈壓作為參考。從圖中可以看出隨著ε取值的不斷減小，波形脈壓的旁瓣水平在不斷下降，說明了本文算法能夠起到相似性約束的作用。

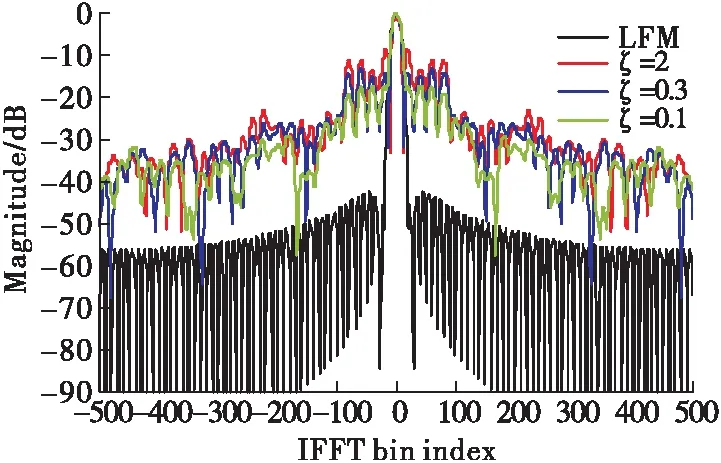
圖8 不同相似性約束下的波形脈沖壓縮圖

對于局部頻譜設計時的SINR變化曲線，ESD，波形幅度和脈壓情況，具有和全局設計時幾乎相同的結果，本文不再一一展示，主要區別或優勢是局部頻譜設計可以精確控制特定頻帶上的允許干擾能量，而全局頻譜設計則只能保證所有特定頻帶上總的干擾能量小于設定的門限值。

4.4 全局頻譜設計和局部頻譜設計比較

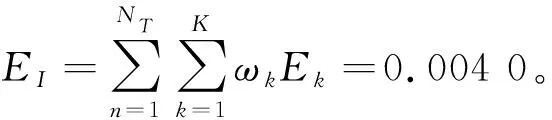
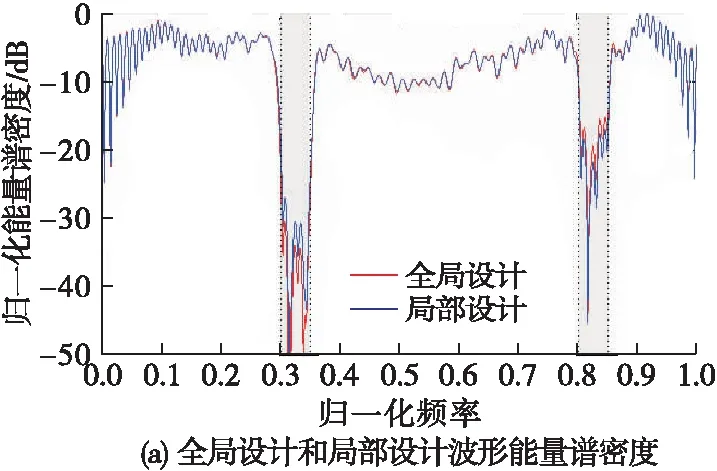
圖9 全局設計和局部設計波形能量譜密度

表3 全局設計和局部設計對應頻帶能量值

圖9給出了全局設計和局部設計下的ESD。從圖中可以看出，無論哪種設計方法第一頻帶的能量下降程度都更高，說明了第一頻帶的優先級更高。但是對于第一頻帶而言全局設計要比局部設計下降的能量更多，而對于第二頻帶而言全局設計則比局部設計下降的能量要少。

表4給出了分別通過全局設計和局部設計后兩個頻帶上的能量值，從表中數據可以發現，具體到每個頻帶上而言，全局設計后第一頻帶能量要遠小于設定值E1，說明第一頻帶能量下降過多，而第二頻帶能量則又大于設定值E2，說明第二頻帶能量下降太少。然而通過局部設計后，每個頻帶上的能量都符合各自頻帶設定的門限要求。以上說明了局部設計能夠精確控制不同頻帶的能量，相比較全局設計更具有優勢。

5 結語

本文研究了機載MIMO雷達在地雜波環境下的頻譜共存波形設計問題，旨在于通過波形設計的方法進一步增強雷達對地面動目標的檢測性能，同時能夠實現雷達與通信系統之間的頻譜共存。在設計階段，本文對波形進一步施加了峰均比約束，并研究了全局頻譜設計和局部頻譜設計兩種設計方法。針對這一復雜的多約束非凸聯合優化問題，考慮到現有算法的局限性，本文提出了一種新穎的循環迭代算法。仿真分析部分首先將本文算法和現有算法進行了性能比較，證明了所提算法具有更低的運算復雜度，然后具體評估了本文算法在全局頻譜設計時不同峰均比約束對SINR，ESD以及波形幅度的影響，不同相似性約束對SINR，ESD以及波形脈壓特性的影響，最后定量比較了全局設計和局部設計的各自特點。仿真結果證明了所提算法的有效性。未來可能的工作是研究在目標先驗信息不確定時的機載MIMO雷達穩健波形設計[15-16]。