基于北斗的地基增強系統多基準一致性檢驗算法

胡 杰, 嚴勇杰, 石瀟竹

(1.中國電子科技集團公司第二十八研究所, 南京, 210007；2.空中交通管理系統與技術國家重點實驗室, 南京, 210007)

全球導航衛星系統(Global Navigation Satellite System, GNSS)現已逐步完善，它憑借全球、全天候、高精度等優點受到越來越多的應用[1]。國際民航組織計劃利用衛星導航系統替代傳統地面導航設備，降低航空導航成本，增加航路設計[2-3]。地基增強系統(Ground Based Augmentation System, GBAS)在采用差分技術提高衛星信號測距精度的基礎上，增加一系列完好性監測算法，提高了導航系統的完好性和可用性[4-5]。隨著我國北斗衛星導航系統(Beidou Navigation System, BDS)在民航領域中的應用范圍越來越廣泛[6]，國內科研院所正在積極開展基于BDS的GBAS差分定位與完好性監測等研究工作，如中電54所、28所等圍繞衛星信號完好性監測[7]、機載差分定位[8]等開展研究，北京航空航天大學王志鵬[9]、薛瑞[10]等人一直致力于基于雙頻多星座的III類精密進近與著陸衛星導航關鍵技術研究，對我國BDS在民用航空導航中的應用具有積極的引導作用。

Stanford大學給出了GBAS地面系統完好性監視平臺仿真模型，包括信號質量監測、數據質量監測以及觀測質量監測等，并計算通過一系列完好性監視后的衛星信號偽距差分校正值[11]。為了確保多個基準站計算得到的差分校正具有一致性，需要在廣播差分校正值前進行多基準一致性檢驗(Multiple Reference Consistency Check, MRCC)，以隔離可能存在故障的接收機。RTCA DO245[12]標準中給出了一種基于極大似然估計準則的MRCC算法，該算法通過比較各個基準站的差分校正值并計算其B值以判別基準站接收機是否存在故障。Dautermann[13]將該方法應用于德國DLR機構研制的GBAS地面系統中心處理單元中，并指出可以根據B值的標準差評估GBAS地面系統精度，但是對于B值門限值的設定方法并未提及。李亮[14]、徐軻[15]指出由于各個基準站之間存在相關性，基于極大似然估計準則的MRCC算法無法有效區分故障來源，因此提出了一種基于Kalman濾波的B值計算新方法，該方法是建立在假設某一基準站接收機發生故障的概率為零的基礎之上，在實際中該假設一般難以成立。胡杰[16]、劉軍[17]等人針對傳統MRCC算法無法檢測故障衛星的問題，提出了一種GBAS中基于導航監測的B值修正算法，由分析可知，地面系統經過一系列完好性監測后，已經將衛星故障予以排除，但該算法存在冗余，并沒有有效解決B值相關性問題。

針對上述問題，本文提出了一種基于高斯膨脹法的B值門限值計算方法，并利用實驗室研制的GBAS原型系統進行了驗證實驗。

1 基于極大似然估計準則的MRCC算法

假設GBAS地面系統有M個基準站，經過一系列完好性監測后可用衛星個數為N。基準站精確位置信息已知，利用已知點位置與衛星空間坐標可以計算得到第j顆衛星與第i個基準站之間距離為R(i,j)，進一步與經載波相位平滑后的偽距進行差分可以得到平滑偽距的差分校正值為：

PRSC(i,j)=PRS(i,j)-R(i,j)+τ(i,j)

(1)

式中：i為第i個基準站；j為第j顆衛星；PRS為經載波相位平滑后的偽距觀測值；R為星站之間真實距離；為衛星鐘差校正值。

由式(1)計算得到的差分校正值中包含接收機鐘差，因此需要進一步消除該項誤差。對于第i個基準站而言，其所有可觀測衛星的接收機鐘差大小相同，因此可以利用差分校正值估計該接收機鐘差，進一步可得：

(2)

(3)

式中：PRSCA為補償接收機鐘差后差分校正值；PRCORR為地面系統最終播發的差分校正值；c(j)為基準站接收機與機載接收機之間關于第j顆衛星的公共偽距誤差；Sc為可用衛星集合;Si為可用基準站集合。

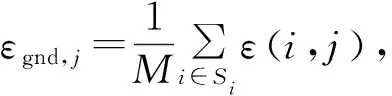
(4)

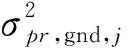
GBAS中心處理單元廣播差分校正值前必須確保所有基準站計算的校正值具有一致性，因此需要對多個基準站的一致性進行檢驗。文獻[12]中給出了GBASB值計算方法，同時規定只要任意一基準站的B值超過設定門限值則需排除該通道，B值計算公式為：

(5)

式中：BPR(i,j)表示第i個基準站所觀測到的第j顆衛星的B值。

進一步可以利用B值的標準差σB對GBAS地面系統精度進行評估，其關系可表示為：

(6)

式中：σB為地面系統計算得B值的標準差，σpr, gnd、PRCOOR以及B值最終通過VDB電臺廣播給機載用戶，以實時計算飛機位置和保護級。

2 GBAS B值理論分析

GBAS地面系統中MRCC算法主要用于檢測地面基準站生成的偽距差分校正值是否具有一致性，通過計算各個基準站對應可見衛星的B值，以隔離其中不具備一致性的差分量。

令Yij=PRsc(i,j)，其中，i=1,2,...,M，j=1,2,...,N，假設M=4，N=4，則總觀測量個數為16，如表1所示，Y·j/M、Yi·/N、Y../MN分別表示列均值、行均值以及總均值。

表1 平滑偽距的差分校正值列表形式

Zij=PRSCA(i,j)=Yij-Yi·/N

(7)

由式(7)以及表1定義可得：

Z·j=Y·j-Y··/N

(8)

將式(2)、式(7)和式(8)帶入式(5)可得：

(9)

假設Yij的均值為μ;αi表示第i個基準站接收機誤差;βj表示第j顆衛星誤差，則Yij可表示為：

Yij=μ+αi+βj

(10)

當M=4，N=4時，式(10)可寫成如下方程形式：

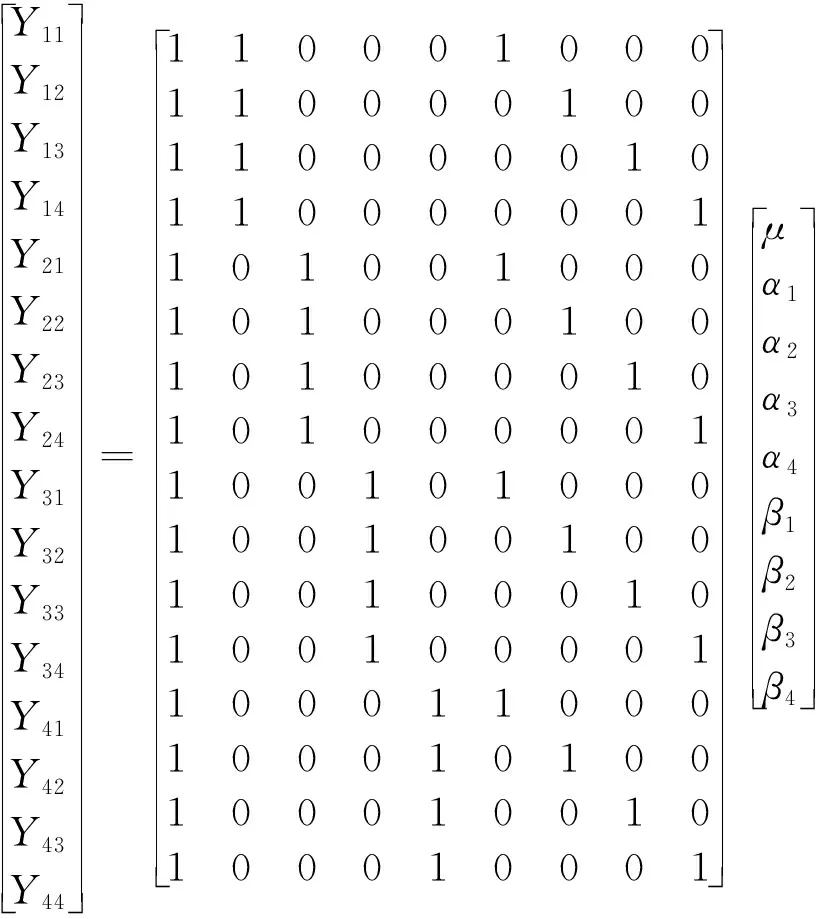
(11)

將式(11)寫成矩陣形式，即：

Y=GX

(12)

利用最小二乘法可以得到變量X的估計值為：

(13)

進一步根據GBAS線性模型最小二乘估計方法可得[18]：

(14)

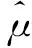
將式(14)帶入式(9)，B值可表示為：

(15)

由式(15)可以看出，B值的大小體現了基準站接收機故障以及衛星故障引起的偽距差分校正值的偏差多少。當基準站接收機和衛星無故障時，B值是偽距差分校正值與其均值的偏差，其數值在較小的范圍內變化，一旦出現任何故障，B值將會大幅跳變，因此通過設定的門限值能夠將故障予以檢測。

傳統基于B值的處理算法無法區分故障來源，針對該問題本文給出了一種能夠區分故障來源的MRCC算法處理流程，如圖1所示。假設地面基準站個數為4，由圖1可以看出，地面系統經過一系列完好性監測后形成可用衛星集合，當可用衛星個數小于4顆時，地面系統告警，表示此時GBAS不可用。當可用衛星個數大于4顆時，則分別計算每顆衛星對應4個基準站的B值，并與設定的門限值進行比較，如果B值在門限值范圍以內，說明通過一致性檢驗，否則需要將其中最大B值對應的基準站予以移除，然后計算剩余基準站對應可見衛星的B值，并進行判別，如果B值不超過門限值，則說明剩余3個基準站通過一致性檢驗，否則說明地面系統可用基準站個數小于3，不滿足系統完好性需求并告警。

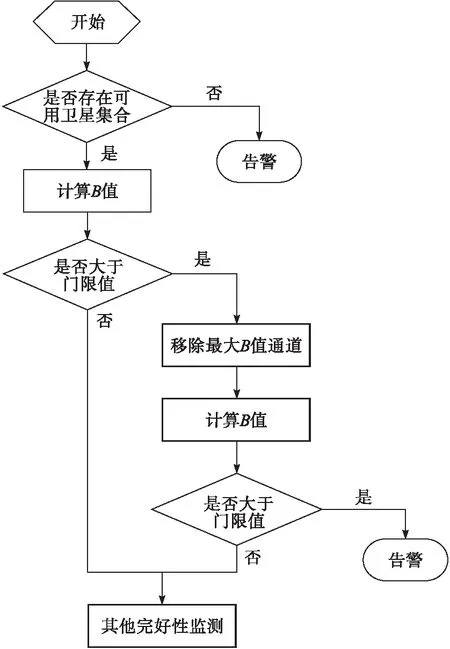
圖1 MRCC算法流程

3 基于高斯膨脹法的門限值計算方法

為了判別B值是否異常，需要確定適合的門限值，本文提出一種基于高斯膨脹法的檢測門限值計算方法，具體實現過程如下：

步驟1根據GBAS地面系統4個基準站處理得到的偽距差分校正值計算B值，并進行預處理，確保所得樣本數據具有較好的一致性。

步驟2以10°為區間劃分步驟1中所計算得B值，并分別計算其均值μ(θ)和標準差σ(θ)，θ表示相應衛星仰角大小。

步驟3利用多項式擬合衛星仰角區間0°～90°內其他角度均值及標準差。

步驟4利用步驟3中擬合得到的B值均值和標準差對樣本數據進行歸一化，具體計算如下：

(16)

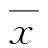
步驟5繪制歸一化后B值的分布直方圖，并計算各個樣本區間概率密度值。

步驟6根據步驟5中計算得概率密度值繪制概率密度分布曲線，并在圖中加載均值為0，標準差為1的標準正態分布曲線，然后對標準正態分布曲線進行膨脹，直至膨脹曲線包絡樣本數據概率密度曲線兩側，由此可得膨脹系數。

確定好膨脹系數后，根據衛星仰角可以得到對應角度下B值的均值和標準差，由式(17)可以得到B值門限值為：

Threshold(θ)=μ(θ)±Kffd·f·σ(θ)

(17)

式中：μ(θ)、σ(θ)分別表示衛星仰角為θ時地面系統B值的均值和標準差;Kffd為乘數因子;為滿足I類精密進近導航完好性需求，取值為6;f為計算得膨脹系數[19]。

利用實驗室GBAS平臺采集一組BDS衛星數據，實驗時間為2019年5月17日8∶00至2019年5月18日8∶00，總時長為24 h，按步驟1～6計算得到膨脹系數，圖2為歸一化后的B值概率密度分布曲線，其中藍色點線為實際過程數據的概率分布，紫色實線為標準高斯正態分布概率密度曲線，紅色點畫線為經過高斯膨脹后的概率密度曲線，由圖2可得對應的膨脹系數f=1.251。

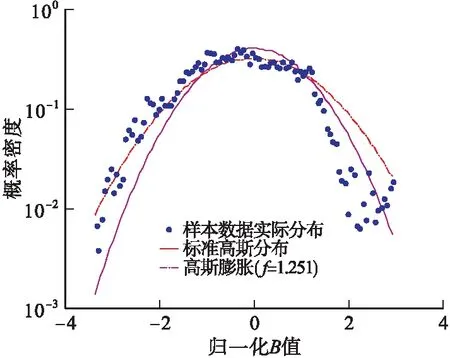
圖2 歸一化B值概率密度曲線

4 驗證實驗

4.1 實驗環境

文中實驗室于2017年初研制了GBAS原型樣機，可實時監測BDS/GPS衛星狀態。GBAS地面系統包括：4個基準站及相應衛星接收天線、中心處理單元以及VDB發射電臺等，軟件部分主要包括以下4個進程，如圖3所示。

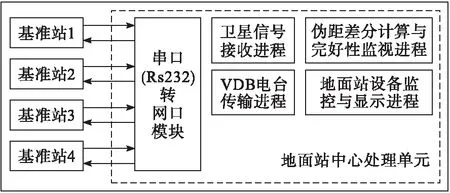
圖3 中心處理單元模塊

4.2 實驗結果分析

GBAS地面系統4個基準站接收衛星信號，并分別計算每個基準站對應可觀測衛星的PRSCA和B值，圖4和圖5分別為2019年6月1日4個基準站對應6號衛星的PRSCA和B值及其門限值曲線，圖6為利用B值計算得地面系統校正值誤差標準差隨衛星仰角變化曲線，圖中紅色實線為根據RTCA DO245計算得GBAS地面系統精度等級，說明實驗室研制的GBAS原型樣機具備A級精度。

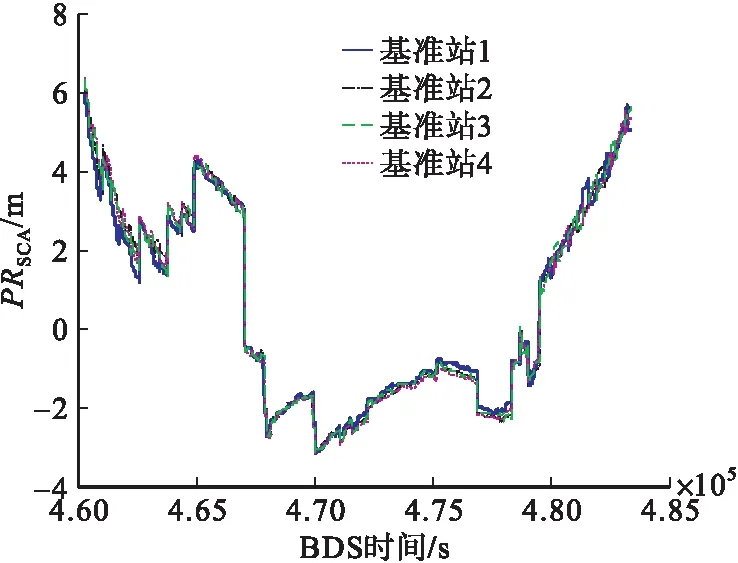
圖4 6號衛星對應4個基準站偽距差分校正值

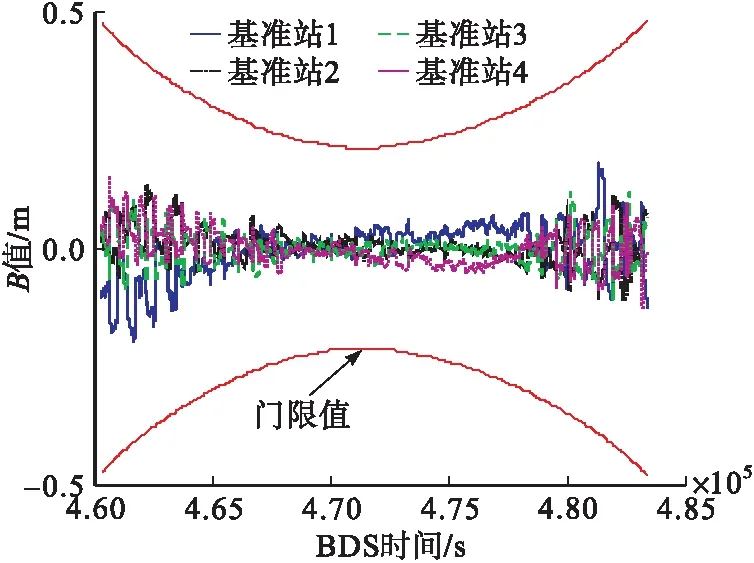
圖5 6號衛星對應4個基準站的B值及其門限值

由圖4～5可以看出，6號衛星在該時間段內的PRSCA具有較好的一致性，因此其B值沒有超出設定的門限值，通過一致性檢驗，進一步對4個基準站偽距差分校正值進行平均可以得到該時間段內6號衛星所播發的PRCORR。由圖6可以看出，隨著衛星仰角變大，偽距所受多路徑以及電離層干擾影響逐漸變小，因此對應的差分校正值誤差的標準差也逐漸變小，數據結果與理論分析一致。

為進一步對本文提出的多基準一致性檢驗算法進行驗證，將基準站1對應的接收機偽距觀測值在歷元10 000至12 000之間(對應的BDS周內時間為470 288～472 288 s)注入5 m測量誤差，以此模擬基準站1接收機故障，為方便對比分析，同樣選用6號衛星的數據進行分析，圖7和圖8為歷元10 000至12 000之間6號衛星的PRSCA和B值及其門限值曲線，圖9為移除基準站1后6號衛星對應3個基準站B值變化曲線。

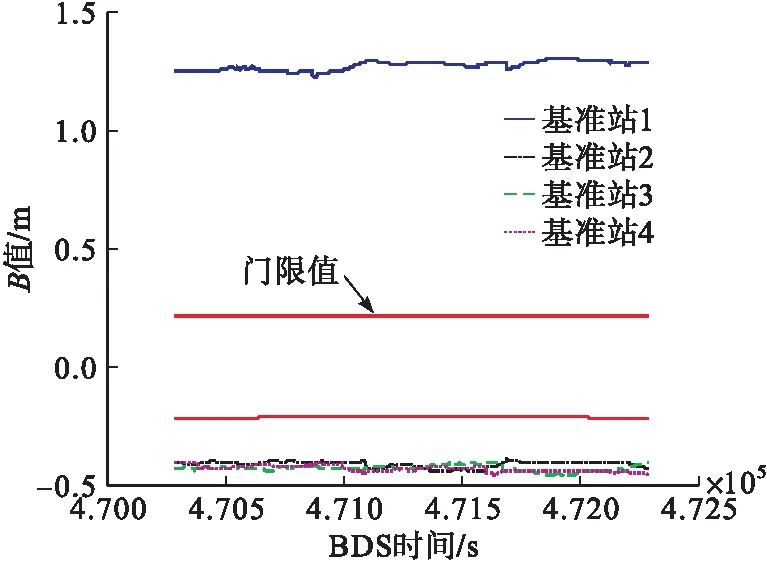
圖8 基準站1接收機故障時6號衛星的B值及其門限值

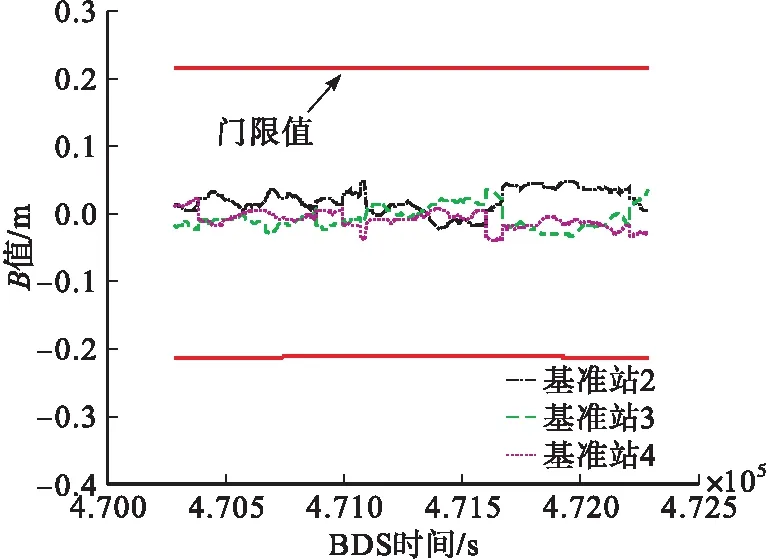
圖9 移除基準站1接收機后6號衛星的B值及其門限值

由圖7、圖8可以看出，在470 288 s至472 288 s之間，當基準站1接收機發生故障時，對應的B值會發生較大幅度的跳變，同時在該時間段內，其他3個基準站對應的B值也出現較為明顯的變化，超出了檢測門限值范圍，因此無法區分故障接收機。進一步根據本文圖1給出的MRCC算法流程，通過比較4個基準站B值的大小，可以將基準站1予以移除，然后計算得到剩余3個基準站的B值，由圖9可以看出，基準站2～4的B值在門限值范圍以內，說明此時有3個基準站接收機可用，從而實現了故障接收機的檢測與隔離。

5 結語

GBAS地面系統中MRCC算法主要用于檢測地面基準站接收機計算得到的差分校正值是否具有一致性，針對傳統基于極大似然估計準則的MRCC算法無法區分GBAS地面系統基準站接收機故障來源問題，本文在對GBASB值計算理論分析的基礎上，給出了一種能夠有效確定接收機故障的MRCC算法處理流程，并提出了一種基于高斯膨脹法的B值門限值計算方法。通過實驗室研制的GBAS原型系統驗證了所提出方法的有效性，地面系統接收機無故障時，B值在門限值以內，一旦某個基準站接收機發生故障，則能夠有效識別該故障并進行隔離，后續需要進一步對該方法的完好性進行評估。